浙教版八年级下册5.3正方形(2)课件(共14张PPT)
文档属性
| 名称 | 浙教版八年级下册5.3正方形(2)课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
教八年下鲁妥行边派
53正方形(2)
选中下面参数技+号增加选代次数技号减少选代数
1=900
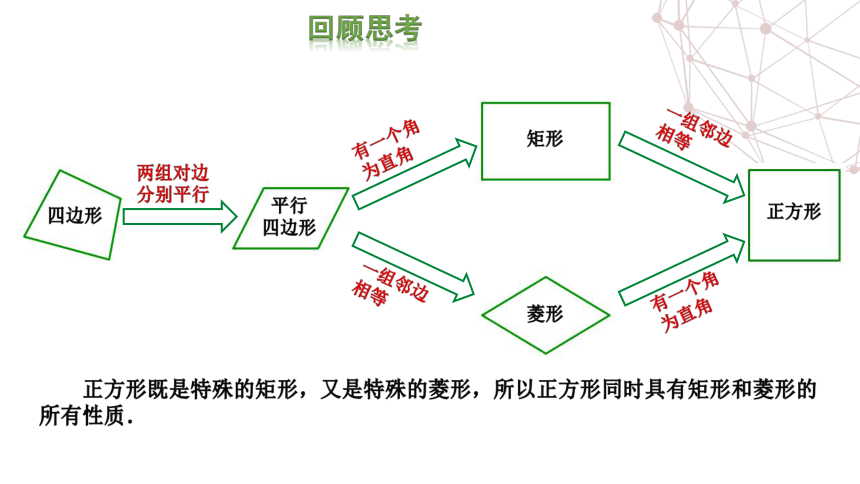
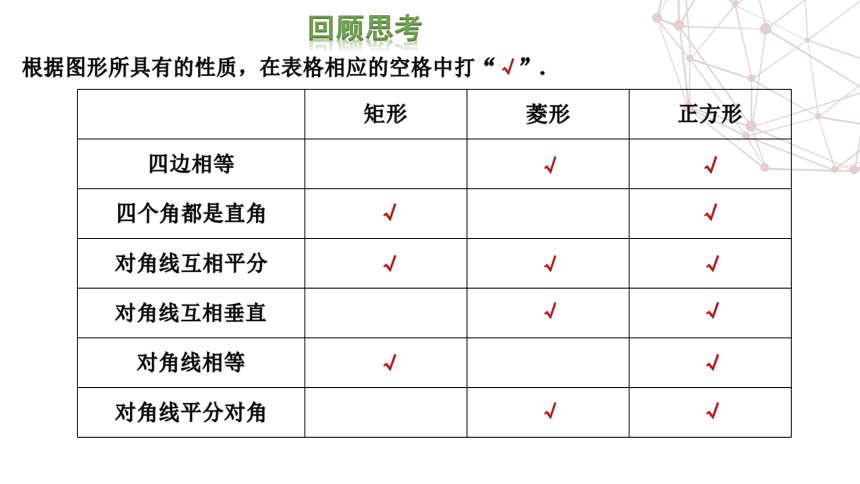
回墨考
两组对边
分别平行
有一个角
月
的的
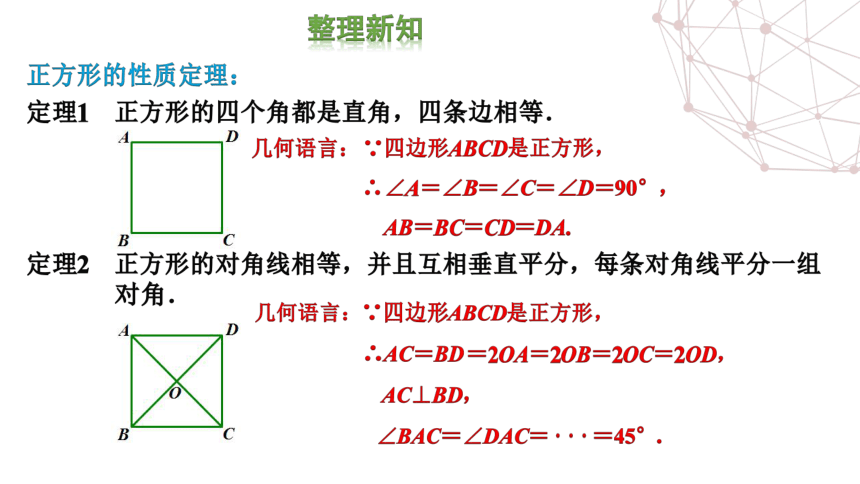
鶉理新纽
正方形的性质定理:
的个角是角,
几何语言:
四边形ABCD是正方形
∠A=∠B=∠C=∠D=90°
AB-BC-CDEDA
几何语言:
四边形ABCD是正方形,
。AC=BD
AC⊥BD,
2OA=20B=20C=20D
∠BAC=∠DAC
45°
性靥缝桠
有的
(D)
XA2
NSA
有的
1)个
B)
X2
L
TEE
有个的
B角分
H
D
E
B
F
C
I:K,EIE1BCDH,
GXT2BD
E
E(.
BO
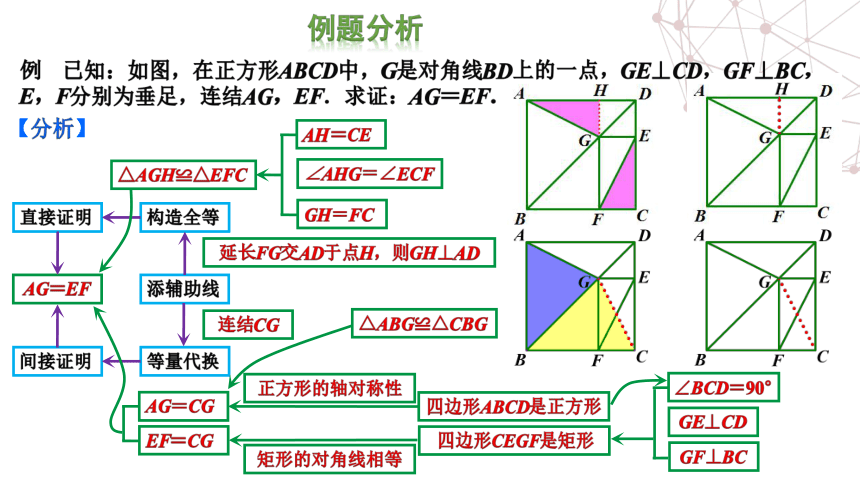
分析】
鹭分析
△ABG≌△CBG
∠BCD=90°
正方形的轴对称性
矩形的对角线相等
HG=∠ECF
四边形ABCD是正方形
四边形CEGF是矩形
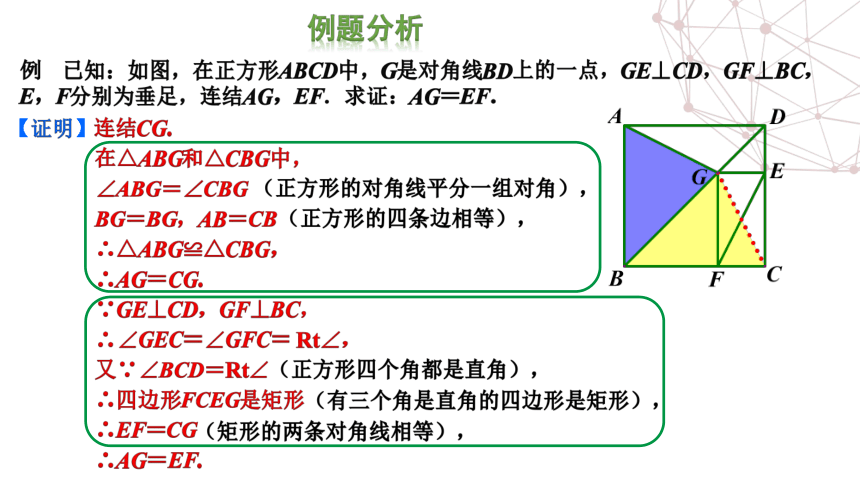
连结CG
延长FG交AD于点H,则GH⊥AD
△AGH≌△EFC
连结CG
在△ABG和△CBG中,
.AG=CG
GE⊥CD,GF⊥BC,
又:∠BCD=Rt∠
四边形FCEG是矩形
。EF=CG
AG=EE
ABG=∠CBG
BG-BG,
ABECB
△ABG≌△CBG,
∠GEC=∠GFC=Rt∠,
I:K,EIE1BCDH,
GXT2BD
E
E(.
BO
鹭追闾
D
E
B
F
C
1的
3的为
AG-EG+FG
(的
【追问】
矩形CEGF的周长=2×正方形ABCD的边长=8
2)B,G的
AB=EG+FG
EF最小值
AG⊥BD
定一动型
两动型
AG的最小值
EF的最小值
方程思想
数形结合
转化思想
对称思想
中耋喜
2017(0为
GEEXABD,
GE
CD,GFI
BC1D1500m
3,的
【解析
小敏的路程=
BATAG+GE
小聪的路程=
BALAD+DE+EF
4600(m)
拓握升
D
B
D
B
B为
(1)若点M在正方形内
(2)若点M在正方形外
分类讨论
B(D中BC(F(,(D
2)的为D的
D
F
B
E
方程思想
B(D中
CBDN
是B,B(的cm(3cm,OFOF,F
教八年下鲁妥行边派
53正方形(2)
选中下面参数技+号增加选代次数技号减少选代数
1=900
回墨考
两组对边
分别平行
有一个角
月
的的
鶉理新纽
正方形的性质定理:
的个角是角,
几何语言:
四边形ABCD是正方形
∠A=∠B=∠C=∠D=90°
AB-BC-CDEDA
几何语言:
四边形ABCD是正方形,
。AC=BD
AC⊥BD,
2OA=20B=20C=20D
∠BAC=∠DAC
45°
性靥缝桠
有的
(D)
XA2
NSA
有的
1)个
B)
X2
L
TEE
有个的
B角分
H
D
E
B
F
C
I:K,EIE1BCDH,
GXT2BD
E
E(.
BO
分析】
鹭分析
△ABG≌△CBG
∠BCD=90°
正方形的轴对称性
矩形的对角线相等
HG=∠ECF
四边形ABCD是正方形
四边形CEGF是矩形
连结CG
延长FG交AD于点H,则GH⊥AD
△AGH≌△EFC
连结CG
在△ABG和△CBG中,
.AG=CG
GE⊥CD,GF⊥BC,
又:∠BCD=Rt∠
四边形FCEG是矩形
。EF=CG
AG=EE
ABG=∠CBG
BG-BG,
ABECB
△ABG≌△CBG,
∠GEC=∠GFC=Rt∠,
I:K,EIE1BCDH,
GXT2BD
E
E(.
BO
鹭追闾
D
E
B
F
C
1的
3的为
AG-EG+FG
(的
【追问】
矩形CEGF的周长=2×正方形ABCD的边长=8
2)B,G的
AB=EG+FG
EF最小值
AG⊥BD
定一动型
两动型
AG的最小值
EF的最小值
方程思想
数形结合
转化思想
对称思想
中耋喜
2017(0为
GEEXABD,
GE
CD,GFI
BC1D1500m
3,的
【解析
小敏的路程=
BATAG+GE
小聪的路程=
BALAD+DE+EF
4600(m)
拓握升
D
B
D
B
B为
(1)若点M在正方形内
(2)若点M在正方形外
分类讨论
B(D中BC(F(,(D
2)的为D的
D
F
B
E
方程思想
B(D中
CBDN
是B,B(的cm(3cm,OFOF,F
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
