1.2数轴、相反数和绝对值知识点讲解+同步练习 2021—2022学年沪科版数学七年级上册
文档属性
| 名称 | 1.2数轴、相反数和绝对值知识点讲解+同步练习 2021—2022学年沪科版数学七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 807.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 00:00:00 | ||
图片预览

文档简介
1.2
数轴、相反数和绝对值
[键入文档标题]
(
8
)
(
9
)
必备知识点
知识点一
数轴
1.数轴的定义
规定了原点、正方向和单位长度的直线叫做数轴。
注意:
①数轴是一条向两方无限延伸的直线;②数轴三要素:原点、正方向、单位长度;③原点的位置、正方向和单位长度大小的确定都是根据需要人为规定的,习惯上规定向右为正方向。
2.数轴的画法
例1下列图形是数轴的是( )
牢记四点看数轴:①是否有原点;②是否有正方向;③单位长度是否统一;④标的数字顺序是否正确。
知识点二
数轴上的点与有理数的对应关系
1.对应关系
①一般地,任意一个有理数,都可以用数轴上的一个点来表示;
②0用原点表示,原点右边
的数表示正数,原点左边的数
表示负数;
③但数轴上的点表示的数不一定都是有理数,它们之间不是一一对应的关系,比如π这样的数也能在数轴上表示。
2.数轴的两个基本应用
例2在数轴上画出表示下列各数的点:
3,
-2,
-3.5,
1,
0
例3指出数轴上A,B,C,D,E各点分别表示什么数?
提示:①画点时标实心圆点,数和字母要写在对应点的正上方;②由数描点:先由符号确定位置,再由距离找到点;③由点读数:先由位置确定符号,再由距离读出数。
知识点三
相反数
1.相反数的概念
只有符号不同的两个数互为相反数。特别的,0的相反数是0。
提示:①相反数是成对出现的,不能单独存在;②任何一个有理数都只有一个相反数;③“只有”指的是除符号不同外,其他完全相同;④0的相反数是0,相反数是其本身的只有0。
2.
几何意义
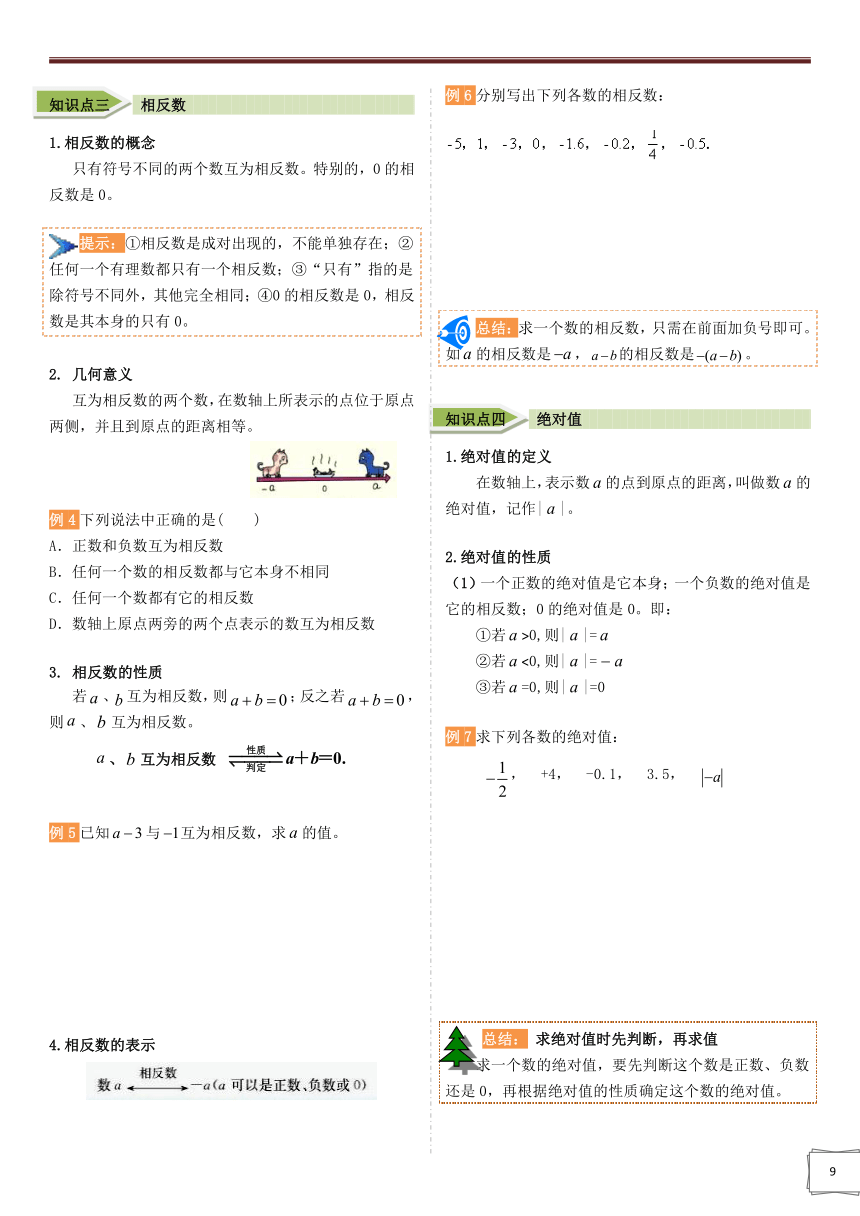
互为相反数的两个数,在数轴上所表示的点位于原点两侧,并且到原点的距离相等。
例4下列说法中正确的是( )
A.正数和负数互为相反数
B.任何一个数的相反数都与它本身不相同
C.任何一个数都有它的相反数
D.数轴上原点两旁的两个点表示的数互为相反数
3.
相反数的性质
若、互为相反数,则;反之若,则、互为相反数。
、互为相反数
例5已知与互为相反数,求的值。
4.相反数的表示
例6分别写出下列各数的相反数:
总结:求一个数的相反数,只需在前面加负号即可。如的相反数是,的相反数是。
知识点四
绝对值
1.绝对值的定义
在数轴上,表示数的点到原点的距离,叫做数的绝对值,记作||。
2.绝对值的性质
(1)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。即:
①若>0,则||=?
②若<0,则||=
③若=0,则||=0
例7求下列各数的绝对值:
,
+4,
-0.1,
3.5,
总结:
求绝对值时先判断,再求值
求一个数的绝对值,要先判断这个数是正数、负数还是0,再根据绝对值的性质确定这个数的绝对值。
拓展:①绝对值是它本身的数是非负数,即若||=,则≥0,即为非负数;绝对值是其相反数的数是非正数,即若||=-,则≤0,即为非正数;②在同一个数轴上,一个数离原点越近,其绝对值越小;离原点越远,其绝对值越大。
(2)绝对值的非负性
任何有理数的绝对值都是非负数,即||≥0。
例8下列各式中无论m为何值,一定是正数的是(
)
A.
|m|
B.
|m+1|
C.
|m|
+1 D.|m|
-1
总结:①几个非负数的和为0,则这几个非负数均为0。即,则;②互为相反数的两个数的绝对值相等;绝对值相等的两个数相等或互为相反数;③在数轴上,点,,表示有理数,,一般地,称为点与点之间距离。
典型例题
题型一
数轴的应用
1.数轴上两点间的距离
典例1在数轴上,到原点的距离等于3的点表示的数是(
)
A.3
B.-3
C.3或-3
D.无法确定
2.借助数轴分析点的移动
典例2(1)点A从数轴上的原点开始运动,先向左移动3个单位长度,再向右移动4个单位长度,此时点A表示的数是
。
(2)若点B在数轴上先向左移动3个单位长度,再向右移动8个单位长度后所得到的点表示的数是3,则点B表示的数是
。
3.数轴上的整数点问题
典例3如图,小明写作业时不慎将两滴墨水滴在作业本上(涂色部分)。根据图中的数值,你能确定被墨迹盖住的整数有哪几个吗?
4.借助数轴解决实际问题
典例4某旅游大巴从旅行社出发,先向西行驶3km到达A景点,再继续向西行驶1km到达B景点,然后向东行驶8km到达C景点,最后回到旅行社。
(1)以旅行社为原点,以向东方向为正方向,用1个单位长度表示1km,画出数轴,并在该数轴上表示出A,B,C三个景点的位置。
(2)C景点距离A景点有多远?
(3)该旅游大巴共行驶了多少路程?
5.与数轴有关的探究题
典例5如图所示,圆的周长为4个单位长度,在圆的四等分点处分别标上字母A,B,C,D,先将圆周上的字母A对应的点与数轴上的数字0所对应的点重合。若将圆沿着数轴向左滚动,则数轴上的-2021所对应的点将与圆周上字母 所对应的点重合;若此时将圆再沿着数轴向右滚动,则数轴上的2022所对应的点将与圆周上字母 所对应的点重合。
题型二
相反数的应用
1.多重符号的化简
典例6化简下列各数:
(1)-
(2)-
(3)+
方法归纳:多重符号的化简方法:
一个数或式子有多重符号时,可根据相反数的性质由内向外化简,也可以根据“-”的个数确定结果的符号,即当一个正数前有奇数个“-”号时,化简结果为负;当一个正数前有偶数个“-”号时,化简结果为正。可简写为:“奇负偶正”
2.利用相反数的概念求值
典例7已知与互为相反数,与互为相反数,且=
-6,则=
。
3.借助数轴解相反数问题
典例8如图①,已知A,B,C,D四个点在一条还没有规定原点的数轴上。
(1)若点A和点C表示的两个数互为相反数,则原点为
。
(2)若点B和点D表示的两个数互为相反数,则原点为
。
(3)若点A和点D表示的两个数互为相反数,请在数轴上表示出原点的位置,用O来表示。
题型三
绝对值的应用
1.根据绝对值的性质确定字母的取值范围
典例9若,则的取值范围是
。
2.与绝对值有关的计算
典例10计算:
(1)|-2|+|+1|;
(2)|-12|-|-8|;
(3)|+3.8|+|-6.2|。
3.运用绝对值的非负性求值
典例11已知,求下面各式的值:(1);
(2)。
4.利用绝对值解决实际问题
典例12正式排球比赛对所使用的排球质量是有严格规定的,检查5个排球的质量,超过规定质量的克数记为正数,不足规定质量的克数记为负数,检查结果如下表:
+15
-10
+30
-20
-40
(1)指出哪个排球质量最好,即质量最接近规定质量;
(2)如果对两个排球进行上述检查,检查的结果分别为p和q,请利用学过的绝对值的知识指出这两个排球中哪个质量好一些。
5.与绝对值相关的阅读理解题
典例13阅读下面的材料,然后解答问题:
我们知道,正数的绝对值是正数,负数的绝对值是它的相反数,0的绝对值是0。用字母表示:当a>0时,|a|=a;当a<0时,|a|=-a;当a=0时,|a|=0。对于a-b,若a>b,则|a-b|>0,此时|a-b|=a-b;若a(1)对于|x-1|,当x>1时,x-1
0,则|x-1|=
;
(2)对于|x-1|,当x<1时,x-1
0,则|x-1|=
;
(3)对于|x-1|,当x=1时,x-1
0,则|x-1|=
;
(4)表示数a,b,c的点如图所示,试化简|b-a|=
;则|c-a|=
。
易错题
求相反数及化简多重符号时出错
典例14求下列各数(或式子)的相反数:
(1)-(-8);
(2)m-n;
(3)m+n
易错题
对绝对值性质理解不透彻
典例15已知两个数,同时满足-6,,则
。
数轴、相反数和绝对值
[键入文档标题]
(
8
)
(
9
)
必备知识点
知识点一
数轴
1.数轴的定义
规定了原点、正方向和单位长度的直线叫做数轴。
注意:
①数轴是一条向两方无限延伸的直线;②数轴三要素:原点、正方向、单位长度;③原点的位置、正方向和单位长度大小的确定都是根据需要人为规定的,习惯上规定向右为正方向。
2.数轴的画法
例1下列图形是数轴的是( )
牢记四点看数轴:①是否有原点;②是否有正方向;③单位长度是否统一;④标的数字顺序是否正确。
知识点二
数轴上的点与有理数的对应关系
1.对应关系
①一般地,任意一个有理数,都可以用数轴上的一个点来表示;
②0用原点表示,原点右边
的数表示正数,原点左边的数
表示负数;
③但数轴上的点表示的数不一定都是有理数,它们之间不是一一对应的关系,比如π这样的数也能在数轴上表示。
2.数轴的两个基本应用
例2在数轴上画出表示下列各数的点:
3,
-2,
-3.5,
1,
0
例3指出数轴上A,B,C,D,E各点分别表示什么数?
提示:①画点时标实心圆点,数和字母要写在对应点的正上方;②由数描点:先由符号确定位置,再由距离找到点;③由点读数:先由位置确定符号,再由距离读出数。
知识点三
相反数
1.相反数的概念
只有符号不同的两个数互为相反数。特别的,0的相反数是0。
提示:①相反数是成对出现的,不能单独存在;②任何一个有理数都只有一个相反数;③“只有”指的是除符号不同外,其他完全相同;④0的相反数是0,相反数是其本身的只有0。
2.
几何意义
互为相反数的两个数,在数轴上所表示的点位于原点两侧,并且到原点的距离相等。
例4下列说法中正确的是( )
A.正数和负数互为相反数
B.任何一个数的相反数都与它本身不相同
C.任何一个数都有它的相反数
D.数轴上原点两旁的两个点表示的数互为相反数
3.
相反数的性质
若、互为相反数,则;反之若,则、互为相反数。
、互为相反数
例5已知与互为相反数,求的值。
4.相反数的表示
例6分别写出下列各数的相反数:
总结:求一个数的相反数,只需在前面加负号即可。如的相反数是,的相反数是。
知识点四
绝对值
1.绝对值的定义
在数轴上,表示数的点到原点的距离,叫做数的绝对值,记作||。
2.绝对值的性质
(1)一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。即:
①若>0,则||=?
②若<0,则||=
③若=0,则||=0
例7求下列各数的绝对值:
,
+4,
-0.1,
3.5,
总结:
求绝对值时先判断,再求值
求一个数的绝对值,要先判断这个数是正数、负数还是0,再根据绝对值的性质确定这个数的绝对值。
拓展:①绝对值是它本身的数是非负数,即若||=,则≥0,即为非负数;绝对值是其相反数的数是非正数,即若||=-,则≤0,即为非正数;②在同一个数轴上,一个数离原点越近,其绝对值越小;离原点越远,其绝对值越大。
(2)绝对值的非负性
任何有理数的绝对值都是非负数,即||≥0。
例8下列各式中无论m为何值,一定是正数的是(
)
A.
|m|
B.
|m+1|
C.
|m|
+1 D.|m|
-1
总结:①几个非负数的和为0,则这几个非负数均为0。即,则;②互为相反数的两个数的绝对值相等;绝对值相等的两个数相等或互为相反数;③在数轴上,点,,表示有理数,,一般地,称为点与点之间距离。
典型例题
题型一
数轴的应用
1.数轴上两点间的距离
典例1在数轴上,到原点的距离等于3的点表示的数是(
)
A.3
B.-3
C.3或-3
D.无法确定
2.借助数轴分析点的移动
典例2(1)点A从数轴上的原点开始运动,先向左移动3个单位长度,再向右移动4个单位长度,此时点A表示的数是
。
(2)若点B在数轴上先向左移动3个单位长度,再向右移动8个单位长度后所得到的点表示的数是3,则点B表示的数是
。
3.数轴上的整数点问题
典例3如图,小明写作业时不慎将两滴墨水滴在作业本上(涂色部分)。根据图中的数值,你能确定被墨迹盖住的整数有哪几个吗?
4.借助数轴解决实际问题
典例4某旅游大巴从旅行社出发,先向西行驶3km到达A景点,再继续向西行驶1km到达B景点,然后向东行驶8km到达C景点,最后回到旅行社。
(1)以旅行社为原点,以向东方向为正方向,用1个单位长度表示1km,画出数轴,并在该数轴上表示出A,B,C三个景点的位置。
(2)C景点距离A景点有多远?
(3)该旅游大巴共行驶了多少路程?
5.与数轴有关的探究题
典例5如图所示,圆的周长为4个单位长度,在圆的四等分点处分别标上字母A,B,C,D,先将圆周上的字母A对应的点与数轴上的数字0所对应的点重合。若将圆沿着数轴向左滚动,则数轴上的-2021所对应的点将与圆周上字母 所对应的点重合;若此时将圆再沿着数轴向右滚动,则数轴上的2022所对应的点将与圆周上字母 所对应的点重合。
题型二
相反数的应用
1.多重符号的化简
典例6化简下列各数:
(1)-
(2)-
(3)+
方法归纳:多重符号的化简方法:
一个数或式子有多重符号时,可根据相反数的性质由内向外化简,也可以根据“-”的个数确定结果的符号,即当一个正数前有奇数个“-”号时,化简结果为负;当一个正数前有偶数个“-”号时,化简结果为正。可简写为:“奇负偶正”
2.利用相反数的概念求值
典例7已知与互为相反数,与互为相反数,且=
-6,则=
。
3.借助数轴解相反数问题
典例8如图①,已知A,B,C,D四个点在一条还没有规定原点的数轴上。
(1)若点A和点C表示的两个数互为相反数,则原点为
。
(2)若点B和点D表示的两个数互为相反数,则原点为
。
(3)若点A和点D表示的两个数互为相反数,请在数轴上表示出原点的位置,用O来表示。
题型三
绝对值的应用
1.根据绝对值的性质确定字母的取值范围
典例9若,则的取值范围是
。
2.与绝对值有关的计算
典例10计算:
(1)|-2|+|+1|;
(2)|-12|-|-8|;
(3)|+3.8|+|-6.2|。
3.运用绝对值的非负性求值
典例11已知,求下面各式的值:(1);
(2)。
4.利用绝对值解决实际问题
典例12正式排球比赛对所使用的排球质量是有严格规定的,检查5个排球的质量,超过规定质量的克数记为正数,不足规定质量的克数记为负数,检查结果如下表:
+15
-10
+30
-20
-40
(1)指出哪个排球质量最好,即质量最接近规定质量;
(2)如果对两个排球进行上述检查,检查的结果分别为p和q,请利用学过的绝对值的知识指出这两个排球中哪个质量好一些。
5.与绝对值相关的阅读理解题
典例13阅读下面的材料,然后解答问题:
我们知道,正数的绝对值是正数,负数的绝对值是它的相反数,0的绝对值是0。用字母表示:当a>0时,|a|=a;当a<0时,|a|=-a;当a=0时,|a|=0。对于a-b,若a>b,则|a-b|>0,此时|a-b|=a-b;若a
0,则|x-1|=
;
(2)对于|x-1|,当x<1时,x-1
0,则|x-1|=
;
(3)对于|x-1|,当x=1时,x-1
0,则|x-1|=
;
(4)表示数a,b,c的点如图所示,试化简|b-a|=
;则|c-a|=
。
易错题
求相反数及化简多重符号时出错
典例14求下列各数(或式子)的相反数:
(1)-(-8);
(2)m-n;
(3)m+n
易错题
对绝对值性质理解不透彻
典例15已知两个数,同时满足-6,,则
。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
