6.2菱形（2）

(共26张PPT)
6.2菱形 (2)
四边形集合
平行四边形集合
菱形集合
矩形集合
平行四边形
菱形
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
菱形 边 对称性 角 对角线
性
质
面积
对边平行
四条边都相等
中心对称图形
轴对称图形
对角相等
对角线互相垂直
对角线互相平分
每一条对角线平分一组对角
用列表形式小结出菱形的性质
1、底乘以高
2、 （a，b表示两条对角线的长度）
学以致用
1、如图，在一种可伸缩的衣帽架中，每个菱形的周长都为100厘米，固定在墙上的两点A、B之间的距离为25厘米，则∠ACB= .
A
B
C
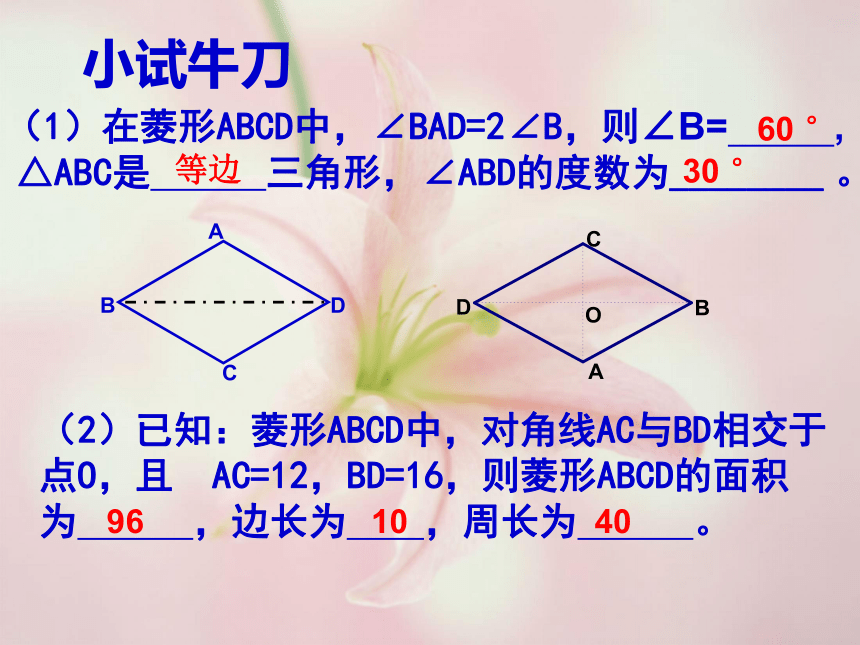
小试牛刀
（2）已知：菱形ABCD中，对角线AC与BD相交于点O，且 AC=12，BD=16，则菱形ABCD的面积为 ，边长为 ，周长为 。
（1）在菱形ABCD中，∠BAD=2∠B，则∠B= , △ABC是 三角形，∠ABD的度数为________ 。
等边
30 °
96
10
40
60 °
A
B
C
D
小试牛刀
（3）在菱形ABCD中∠BAC=30°，BD=6㎝，则 ∠BAD= , ∠ABD= , AB= .
60 °
60 °
6㎝
A
B
C
D
例1 如图，菱形花坛ABCD的边长为20m， ∠ABC＝60度，沿着菱形的对角线修建了两条小路AC和BD，求两条小路的长和花坛的面积（分别精确到0.01m和0.01m2 ）
O
解:∵花坛ABCD是菱形
∴AC⊥BD, ∠ABO= ∠ABC=300
在Rt△OAB中 ,AO=AB= ×20=10(m),
BO= = ≈17.32(m).
∴花坛的两条小路长
AC=2AO=20(m),
BD=2BO ≈34.64(m).
花坛的面积
S菱形ABCD=4× S △OAB=AC×BD ≈346.40(m2).
1、已知,在菱形ABCD中,∠BAD= ,现将一块含 角的三角尺AMN(其中∠NAM= )叠放在菱形上,然后将三角尺绕点A旋转.在旋转过程中,设AM交边BC于点E,AN交边CD于点F,那么BE+DF与AB有着怎样的数量关系 请你通过动手操作、度量、猜想、验证等方法予以探索。
挑战自我
菱形3周朝晖.gsp
2.菱形ABCD中∠ABC=60°,AB=4cm,P为BD上任意一点,E为BC中点,求PE+PC的最小值.
例.如图，将一张边长为4的菱形纸片ABCD固定在一个建立了平面直角坐标系的木板上，A，B在x轴上，D在y轴的正半轴上，C在第一象限， ∠BAD=60° 。
（1）求A、B、C、D的坐标；
（2）求过B、C两点的直线的解析式。
A
D
C
B
x
y
O
E
他是这样做的：将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开即可.你知道其中的道理吗？
如何利用折纸、剪切的方法，既快又准确地剪出一个菱形的纸片？
菱形的判别方法:
一组邻边相等的平行四边形是菱形.
四条边都相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
对角线互相垂直平分的四边形是菱形.
想一想
怎样判别一个四边形(平行四边形)是菱形
判断下列说法是否正确？为什么？
(1)对角线互相垂直的四边形是菱形；
(2)对角线互相垂直平分的四边形是菱形；
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形；
(4)两条邻边相等，且一条对角线平分一
组对角的四边形是菱形．
□ABCD的对角线AC与BD相交于点O，
（1）若AB=AD，则□ABCD是 形； （2）若AC=BD，则□ABCD是 形； （3）若∠ABC是直角，则□ABCD是 形； （4）若∠BAO=∠DAO，则□ABCD是 形。
A
B
C
D
O
矩
菱
矩
菱
菱形的判定
定理:四条边都相等的四边形是菱形.
我思,我进步
已知:如图,在四边形ABCD中, AB=BC=CD=DA.
分析:利用菱形定义和两组对边分别相等的四边形是平行四边形,可使问题得证.
证明:
∵AB=BC=CD=DA,
∴AB=CD,BC=DA.
∴四边形ABCD是平行四边形..
求证:四边形ABCD是菱形.
∵AB=AD,
∴四边形ABCD是菱形.
C
B
D
A
菱形的判定
定理:对角线互相垂直的平行四边形是菱形.
我思,我进步
2
已知:如图,在□ABCD中,对角线AC⊥BD.
求证:四边形ABCD是菱形.
分析:要证明□ABCD是菱形,就要证明有一组邻边相等即可.
证明:
∴AO=CO.
∵AC⊥BD,
∴ DA=DC.
∵四边形ABCD是平行四边形.
∴四边形ABCD是菱形.
D
B
C
A
O
(线段垂直平分线上的点到线段两端点的距离相等)
学以致用
已知，AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F。 求证：四边形AEDF是菱形。
证明:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形
∵DE∥AC,
∴平行四边形AEDF是菱形.
∴∠ADE=∠DAF.
∵AD是△ABC的角平分线,
∴∠DAE=∠DAF.
∴AE=ED.
∴∠DAE=∠ADE.
已知：如图,□ ABCD的对角线AC的垂直平分线与边AD，BC分别交于E，F．
求证：四边形AFCE是菱形
A
B
F
C
D
E
O
如图，顺次连接矩形ABCD各边中点，得到四边形EFGH，求证：四边形EFGH是菱形。
G
G
F
E
D
C
B
A
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,
CE平分∠ACB,交AD于G,交AB于E,EF⊥BC
于F,四边形AEFG是菱形吗
A
C
D
B
F
E
G
如图:将菱形ABCD沿AC方向平移至A1B1C1D1,
A1D1交CD于E,A1B1交BC于F,请问四边形
A1FCE是不是菱形 为什么
A1
B1
C1
D1
A
B
C
D
A
D
C
B
∟
∟
E
F
把两张等宽的纸条交叉重叠在一起，你能判断重叠部分ABCD的形状吗？
思考:
请你动脑筋
菱形的判定
定理:四条边都相等的四边形是菱形.
定理:对角线互相垂直的平行四边形是菱形.
本课 小结
在四边形ABCD中,
∵AB=BC=CD=AD,
∴四边形ABCD是菱形.
∵AC,BD是□ABCD的两条对角线,AC⊥BD.
∴四边形ABCD是菱形.
C
B
D
A
D
B
C
A
O