点、直线与圆的位置关系

(共21张PPT)
点和圆的位置关系有几种？
（1）d（2）d=r 　点在圆上
（3）d>r 点在圆外
用d表示点到圆心的距离
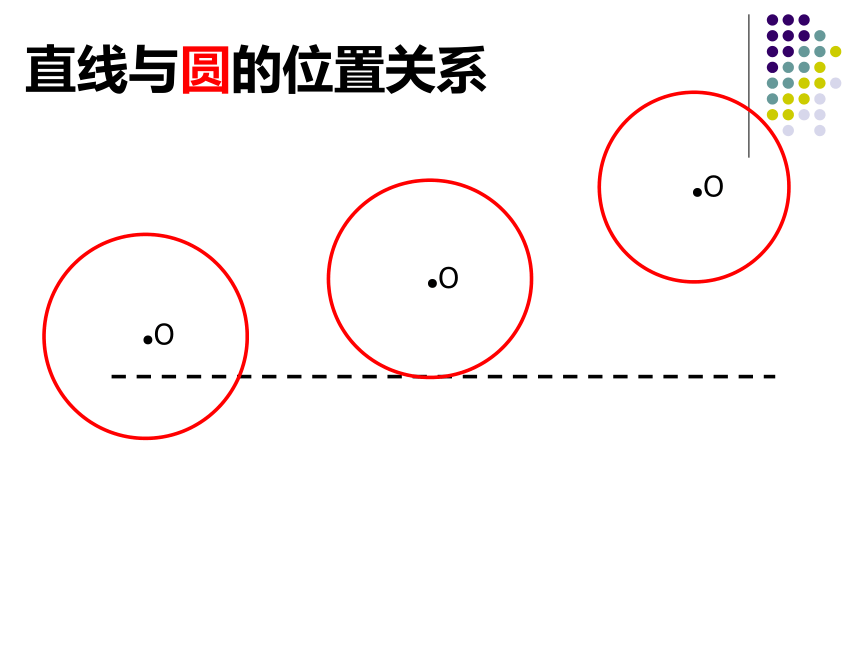
　　“大漠孤烟直，长河落日圆” 描述了黄昏日落时分塞外特有的景象。如果我们把太阳看成一个圆，地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下，直线和圆的位置关系有几种？
观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
直线与圆的位置关系
●O
●O
●O
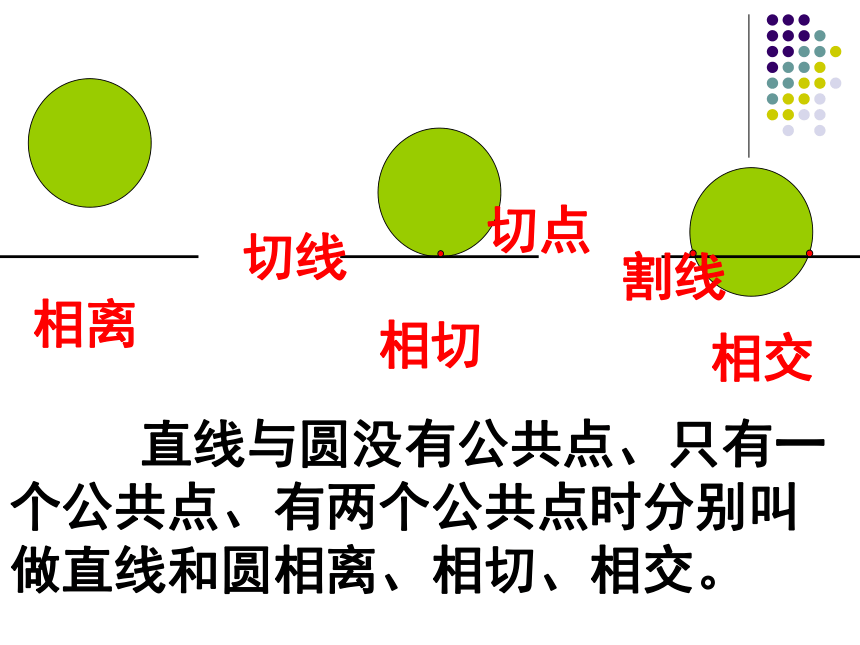
直线与圆没有公共点、只有一个公共点、有两个公共点时分别叫做直线和圆相离、相切、相交。
相离
相交
相切
切点
切线
割线
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
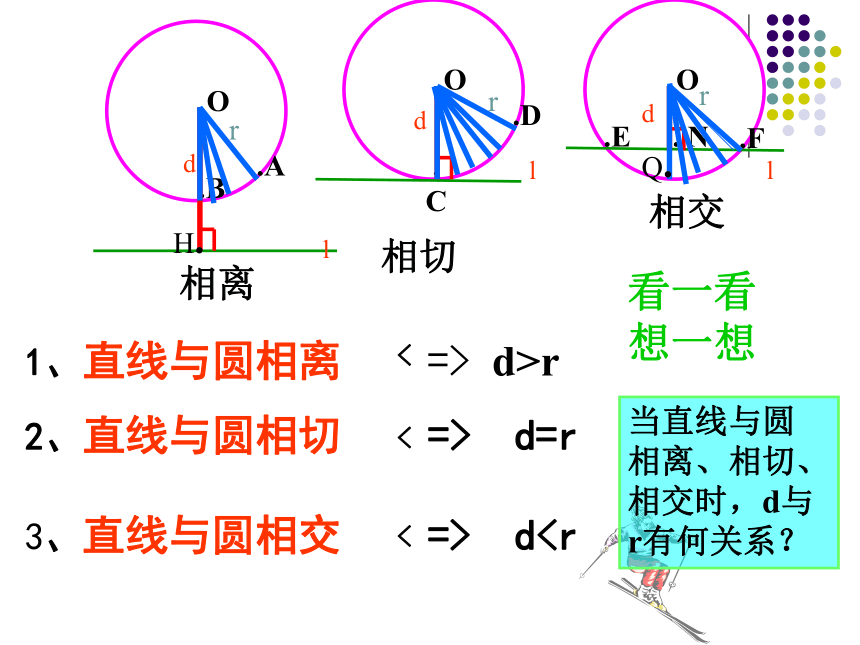
1、直线与圆相离 => d>r
2、直线与圆相切 => d=r
3、直线与圆相交 => d<
<
<
看一看想一想
当直线与圆
相离、相切、
相交时，d与
r有何关系？
l
l
l
.A
.B
.
C
.D
.E
.F
. N
H.
Q.
（2）直线l 和⊙O相切
用圆心到直线的距离和圆半径的
数量关系，来揭示圆和直线的位
置关系。
（1）直线l 和⊙O相离
（3）直线l 和⊙O相交
d>r
d=r
dd
o
r
l
d
o
r
l
o
d
r
l
总结：
判定直线与圆的位置关系的
方法有____种：
(1)根据定义，由直线与圆的公
共点的个数来判断；
(2)根据性质,由圆心到直线的距离d与半径r 的关系来判断。
两
1、已知圆的直径为13cm，
设直线和圆心的距离为d ：
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆　　　, 直线与圆有____个公共点.
相交
相切
相离
2
1
0
2、已知⊙O的半径为5cm，O到直线a的距离为3cm，则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
3、已知⊙O的半径是4cm，O到直线a的距离是4cm，则⊙O与直线a的位置关系是 ___ _。
动动脑筋
相交
相切
两个
4、已知⊙O的半径为6cm，O到直线
a的距离为7cm，则直线a与⊙O的公
共点个数是____。
5、已知⊙O的直径是6cm，O到直线a的距离是4cm，则⊙O与直线a的位置关系是 ___ _。
零
相离
3)若AB和⊙O相交,则
6、已知：⊙O的半径为5cm,
圆心O与直线AB的距离为d,
根据条件填写d的范围:
1)若AB和⊙O相离, 则
2)若AB和⊙O相切, 则
d > 5cm
d = 5cm
d < 5cm
0cm≤
思考：圆心A到
X轴、Y轴的距离
各是多少
.A
O
X
Y
例2：已知⊙A的直径为6，点A的坐标为
（-3，-4），则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。
B
C
4
3
相离
相切
　　如图,已知∠AOB= 30°,M为OB上
一点,且OM=5cm，若以M为圆心,r为半
径作圆,那么:
1)当直线OA与⊙M相离时, r的取值范围是
2)当直线OA与⊙M相切时, r的取值范围是
3)当直线OA与⊙M有公共点时, r的取值范围是
1)当直线OA与⊙M相离时, r的取值范围是
2)当直线OA与⊙M相切时, r的取值范围是
3)当直线OA与⊙M有公共点时, r的取值范围是
0cm < r < 2.5cm
r = 2.5cm
30°
M
B
A
5
C
O
r≥2.5cm
直线与圆的位置关系
公共点个数
公共点名称
直线名称
数量关系
d r
割线 切线 无
交点 切点 无
2
1
0
直线和圆的三种位置关系
相离
相切
相交
1、学法大视野
2、教材P73练习。
思考题：如图,公路MN和PQ在P处交汇, 且∠QPN=300 , 点A处有一所中学, AP=160米, 假设拖拉机行使时, 周围100米以内会受到噪音的影响, 已知拖拉机的速度为18千米／时, 那么学校会受到影响吗 如果会, 受到影响的时间多长
M
N
P
Q
A
思考2：在Rt△ABC中∠C= 90°，AC=3cm，BC=4cm，以C为圆心,r
为半径的圆与直线AB有怎样的关系？
(1) r=2cm
(2) r=2.4cm
(3) r=3cm
D
B
C A
B
C A
D
D
B
C A