2021-2022学年数学浙教版七年级上册4.2 代数式课时同步练习(word解析版)
文档属性
| 名称 | 2021-2022学年数学浙教版七年级上册4.2 代数式课时同步练习(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 148.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 00:00:00 | ||
图片预览




文档简介
《4.2 代数式》课时同步练习2021-2022年数学浙教新版七(上)
一.选择题(共17小题)
1.一件校服,按标价的6折出售,售价是x元,这件校服的标价是( )
A.0.6x元 B.元 C.0.4x元 D.元
2.香蕉的单价为a元/千克,苹果的单价为b元/千克,买2千克苹果和3千克香蕉共需( )元.
A.a+b B.3a+2b C.2a+3b D.5(a+b)
3.笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,2支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花( )元.
A.7x+5y B.6x+6y C.5x+7y D.7x+6y
4.在△ABC中,∠C=90°,D是边BC上一点,连接AD,若∠BAD+3∠CAD=90°,DC=a,BD=b,则AB为( )(用含a,b的式子表示)
A.2a+b B.2b+a C.3b+a D.3a+b
5.某药厂计划对售价为m元的药品进行降价销售,现在有三种方案.方案一:第一次降价10%,第二次降价30%;方案二:第一次降价20%,第二次降价15%;方案三:第一、二次降价均为20%.三种方案哪种降价最多( )
A.方案一 B.方案二 C.方案三 D.不能确定
6.疫情期间因口罩需求急速增长导致生产口罩的原材料价格不断上涨,甲、乙、丙三家药店对同一款售价相同的口罩提价销售:甲药店提价20%销售;乙药店提价15%后再提价5%;丙药店提价10%后再提价10%.若顾客想要购买该口罩,选择最划算的商店是( )
A.甲 B.乙 C.丙 D.都一样
7.苹果打8折后价格是p元/千克,则原价是( )
A.1.25p元/千克 B.p元/千克
C.0.8p元/千克 D.0.2p元/千克
8.某药店在甲工厂以每包a元的价格买进了41盒口罩,又在乙工厂以每包b元(a<b)的价格买进了同样的59盒口罩.如果以每包元的价格全部卖出这种口罩,那么这家药店( )
A.亏损了 B.盈利了
C.不盈不亏 D.盈亏不能确定
9.一个长方形的花园长为a,宽为b,如果长增加x,那么新的花园面积为( )
A.a(b+x) B.b(a+x) C.ab+x D.a+bx
10.笔记本的单价是m元,钢笔的单价是n元,甲买3本笔记本和2支钢笔,乙买4本笔记本和3支钢笔,买这些笔记本和钢笔,甲和乙一共花了多少元?( )
A.7m+5n B.5m+7n C.6m+6n D.7n+5m
11.一个两位数,十位数字是a,十位数字比个位数字小2,这个两位数是( )
A.a(a+2) B.10a(a+2) C.10a+(a+2) D.10a+(a﹣2)
12.东西湖区域出租汽车行驶2千米以内(包括2千米)的车费是10元,以后每行驶1千米,再加0.7元.如果某人坐出租汽车行驶了m千米(m是整数,且m≥2),则车费是( )
A.(10﹣0.7m)元 B.(11.4+0.7m)元
C.(8.6+0.7m)元 D.(10+0.7m)元
13.一条河的水流速度是2.5km/h,某船在静水中的速度是vkm/h,则该船在这条河中逆流行驶的速度是( )
A.(v+2.5)km/h B.(v﹣2.5)km/h
C.(v+5)km/h D.(v﹣5)km/h
14.如图,三角尺(阴影部分)的面积为( )
A.ab﹣2πr B. C.ab﹣πr2 D.
15.某淘宝店家为迎接“双十一”抢购活动,在甲批发市场以每件a元的价格进了40件童装,又在乙批发市场以每件b元(a>b)的价格进了同样的60件童装.如果店家以每件元的价格卖出这款童装,卖完后,这家商店( )
A.盈利了 B.亏损了
C.不赢不亏 D.盈亏不能确定
16.有18米长的木材,要做成一个如图的窗框.如果假设窗框横档的长度为x米,那么窗框的面积是( )
A.x(9﹣x)米2 B.x(18﹣2x)米2
C.x(9﹣3x)米2 D.米2
17.已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成( )
A.10b+a B.ba C.100b+a D.b+10a
二.填空题(共9小题)
18.一条河的水流速度是2km/h,轮船在静水中的速度是vkm/h,用式子表示船在这条河中逆水行驶t小时的路程是 km.
19.如图,(图中长度单位:m),钢管的体积是 m3.
20.两船从同一港口同时出发反向而行,甲船顺水航行了6小时,乙船逆水航行了3小时,两船在静水中的速度都是50km/h,水流速度是akm/h,则两船一共航行了 km.(用含a的式子表示)
21.一个两位数M的个位上的数是a,十位上的数是b,把这个两位数的十位上的数与个位上的数交换位置,所得的新数记为N,则M﹣N= .(用含a、b的式子表示)
22.一个两位数的个位上的数是2,十位上的数是x,用含有x的多项式表示这个两位数为 .
23.某种商品原价是m元,第一次降价打“九折”,第二次降价每件又减20元,第二次降价后的售价是 元.
24.一种商品每件成本是a元,原来按成本增加20%定出价格进销售,一段时间后,由于库存积压减价,按原价的9折出售,则现在每件售价为 元.
25.把六张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为20cm,宽为16cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是 .
26.某公园的成人单价是10元,儿童单价是4元.某旅行团有a名成人和b名儿童;旅行团的门票费用总和为 元.
三.解答题(共2小题)
27.已知四个数a、b、c、d(a<b<c<d),满足|a﹣b|+|c﹣d|=|a﹣d|(n≥3,且为整数).
(1)当n=3时,
①若d﹣a=9,求c﹣b的值;
②对于有理数p,满足|b﹣p|=|a﹣d|,请用含b、c的代数式表示p;
(2)若p=|b﹣c|,q=|a﹣d|,且|p﹣q|=|a﹣d|,求n的值.
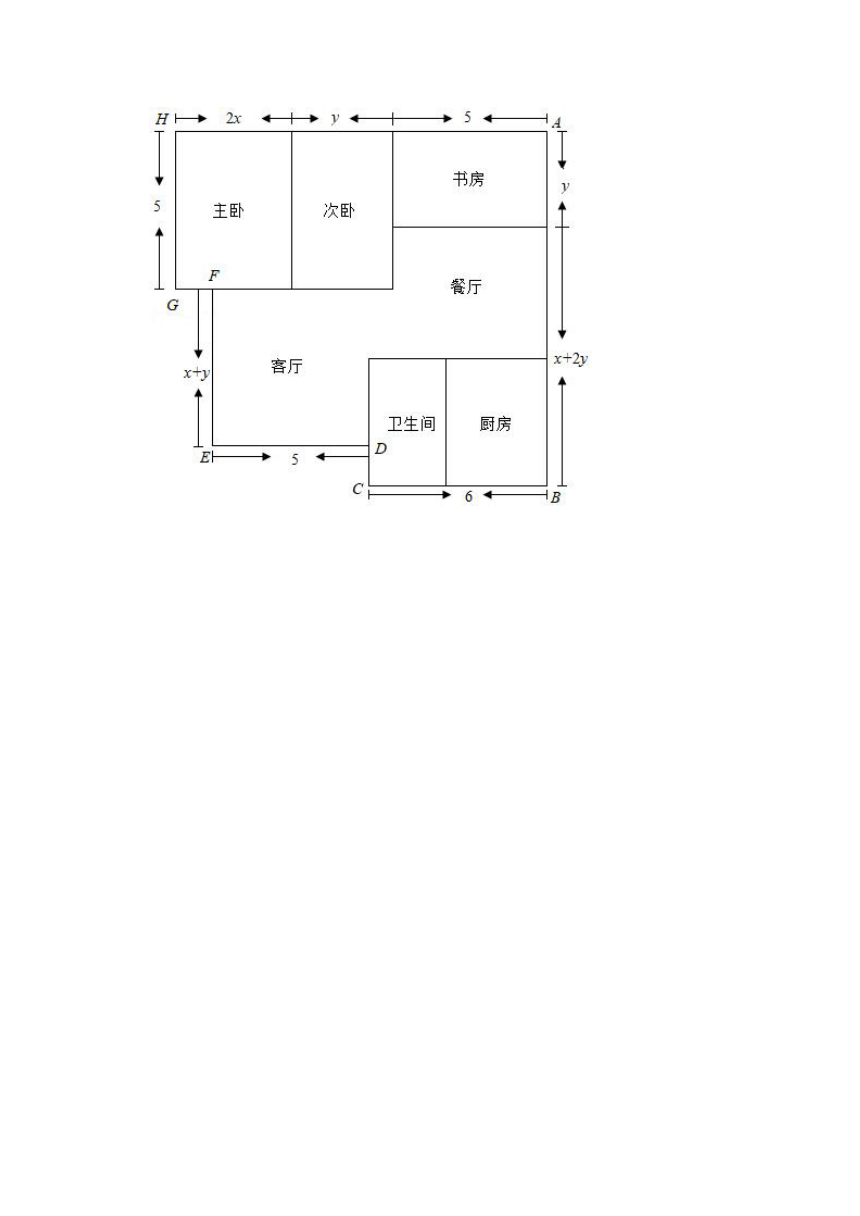
28.某住房户型平面图如下(单位:米),其中,主卧和次卧的面积一共是35m2.现准备铺设地面,主卧次卧和书房铺设木地板,其他区域铺设地砖.
(1)用含x,y的整式表示住房的总面积,直接写出化简后的结果;
(2)若房子右边的宽AB是11m,住房的总面积是多少平方米?
(3)按市场价格,木地板单价为500元/平方米,地砖单价为400元方米,装修公司有A、B两种活动方案,如表:
活动方案 木地板价格 地砖价格 总安装费
A 8折 8.5折 3000元
B 9折 9折 免收
若主卧和次卧的面积之比为4:3.
①直接写出x,y的值;
②选择哪种活动方案,设地面总费用(含材料费及安装费)更低?
参考答案
一.选择题(共17小题)
1.解:x=标价×0.6;
所以,标价=元.
故选:B.
2.解:根据题意得:买2千克苹果和3千克香蕉共需(3a+2b)元,
故选:B.
3.解:小红花的钱为:3x+2y,
小明花的钱为:4x+3y,
则总共花费为:3x+2y+4x+3y=7x+5y.
故选:A.
4.解:如图,延长BC到E,使CE=CD=a,连接AE.
∵∠ACB=90°,
∴∠CAB+∠B=90°,AC⊥CD,
∵∠BAD+3∠CAD=90°,∠BAD+∠CAD=∠BAC,
∴∠B=2∠CAD.
∵CE=CD,AC⊥CD,
∴AE=AD,即△AED是等腰三角形,
∴∠EAC=∠CAD,
∴∠EAD=2∠CAD=∠B,
∴∠EAB=∠B+∠BAD,
∵∠E=∠ADE=∠B+∠BAD,
∴∠E=∠EAB,
∴AB=EB,
∵EB=EC+CD+BD=a+a+b=2a+b,
∴AB=EB=2a+b.
故选:A.
5.解:方案一:m﹣(1﹣10%)(1﹣30%)m=m﹣63%m=37%m,
方案二:m﹣(1﹣20%)(1﹣15%)m=m﹣68%m=32%m,
方案三:m﹣(1﹣20%)(1﹣20%)m=m﹣64%m=36%m,
∵m>0,
∴37%m>36%m>32%m,
∴方案一降价最多.
故选:A.
6.解:可设同一款售价相同的口罩售价为x元,则
甲药店价格为:(1+20%)=1.2x元;
乙药店价格为:(1+15%)(1+5%)x=1.2075x元;
丙药店价格为:(1+10%)(1+10%)x=1.21x元.
故最划算的商店是甲.
故选:A.
7.解:设苹果的原价为x元,则0.8x=p,
∴x=p÷0.8=1.25p(元/千克),
故选:A.
8.解:∵a<b,
∴(41+59)×﹣(41a+59b)
=50a+50b﹣41a﹣59b
=9a﹣9b
=9(a﹣b)<0,
∴这家药店亏损了.
故选:A.
9.解:长增加x,则长为x+a,面积为:b(a+x),
故选:B.
10.解:甲花的钱为:(3m+2n)元,
乙花的钱为:(4m+3n)元,
则甲和乙一共花费为:3m+2n+4m+3n=(7m+5n)元.
故选:A.
11.解:∵一个两位数,十位数字是a,十位数字比个位数字小2,
∴这个两位数是:10a+(a+2).
故选:C.
12.解:由题意可得,
车费是:10+(m﹣2)×0.7=(0.7m+8.6)元,
故选:C.
13.解集:因为船的逆流速度=船在静水中的速度﹣水流速度,
即船的逆流速度是(v﹣2.5)km/h.
故选:B.
14.解集:阴影部分的面积为:S△﹣S圆=ab﹣πr2,
故选:D.
15.解:根据题意列得:在甲批发市场童装的利润为40(﹣a)=20(a+b)﹣40a=20a﹣20b;
在乙批发市场童装的利润为60(﹣b)=30(a+b)﹣60b=30a﹣30b,
∴该商店的总利润为20b﹣20a+30a﹣30b=10a﹣10b=10(a﹣b),
∵a>b,∴a﹣b>0,即10(a﹣b)>0,
则这家商店盈利了.
故选:A.
16.解:结合图形,显然窗框的另一边是 =9﹣x(米).
根据长方形的面积公式,得:窗框的面积是x(9﹣x)平方米.
故选:D.
17.解:两位数的表示方法:十位数字×10+个位数字;三位数字的表示方法:百位数字×100+十位数字×10+个位数字.
a是两位数,b是一位数,依据题意可得b扩大了100倍,所以这个三位数可表示成100b+a.
故选:C.
二.填空题(共9小题)
18.解:船在这条河中逆水行驶t小时的路程是t(v﹣2)km.
故答案为:t(v﹣2).
19.解:外圆柱的体积是:πR2acm3,
内圆柱的体积是:πr2acm3,
钢管的体积是:(πR2a﹣πr2a)cm3.
故答案为:(πR2a﹣πr2a).
20.解:∵甲船顺水航行了6小时,乙船逆水行了3小时,两船在静水中的速度都是50km/h,水流速度是akm/h,
∴甲船顺水的速度是:(50+a)km/h,乙船逆水的速度是:(50﹣a)km/h,
∴两船一共航行了:6(50+a)+3(50﹣a)=300+6a+150﹣3a=(450+3a)km.
答:两船一共航行了(450+3a)千米.
故答案为:(450+3a).
21.解:由题意可得:M=10b+a,N=10a+b,
M﹣N=10b+a﹣(10a+b)
=9b﹣9a.
故答案为:9b﹣9a.
22.解:∵一个两位数的个位上的数是2,十位上的数是x,
∴这个两位数为10x+2.
故答案为:10x+2.
23.解:根据题意得:
第一次降价后的售价是0.9m,第二次降价后的售价是(0.9m﹣20)元.
故答案为:(0.9m﹣20).
24.解:∵每件成本a元,原来按成本增加20%定出价格,
∴每件售价为(1+20%)a=1.2a(元);
现在售价:1.2a×90%=1.08a(元);
故答案是:1.08a.
25.解:设小长方形长为xcm,宽为ycm,由题意得:x+3y=20,
阴影部分周长的和是:20×2+(16﹣3y+16﹣x)×2=104﹣6y﹣2x=104﹣2(3y+x)=104﹣40=64(cm),
故答案为:64cm.
26.解:由题意得:10a+4b,
故答案为:(10a+4b).
三.解答题(共2小题)
27.解:(1)①∵n=3,
∴|a﹣b|+|c﹣d|=|a﹣d|,
∵a<b<c<d,
∴b﹣a+d﹣c=(d﹣a),
∴c﹣b=(d﹣a),
∵d﹣a=9,
∴c﹣b=6;
②∵|b﹣p|=|a﹣d|,
∴b﹣p=±(d﹣a),
∵d﹣a=(c﹣b),
∴b﹣p=±×(c﹣b)=±2(c﹣b),
∴p=2c﹣b或3b﹣2c;
(2)∵|a﹣b|+|c﹣d|=|a﹣d|,a<b<c<d,
∴c﹣b=(1﹣)(d﹣a),
∵p=|b﹣c|,q=|a﹣d|,且|p﹣q|=|a﹣d|,
∴||(1﹣)(d﹣a)|﹣|a﹣d||>|a﹣d|,
∴|a﹣d|>|a﹣d|,
∴2n<12,
∴n<6,
∵n≥3且为正整数,
∴n的值是3或4或5.
28.解:(1)如图,延长BC,HG交于点I,延长DE交HI于点J,
∵住房的总面积S=S长方形ABIH﹣S长方形GFEJ﹣S长方形JDCI,
∵主卧和次卧的面积一共是35m2.
∴5(2x+y)=35,
∴2x+y=7,
∴AH=7+5=12,
∴IC=BI﹣BC=AH﹣BC=12﹣6=6,
∴JE=JD﹣DE=IC﹣DE=6﹣5=1,
∵JI=AB﹣HG﹣EF=y+x+2y﹣5﹣(x+y)=2y﹣5,
∴住房的总面积S=S长方形ABIH﹣S长方形GFEJ﹣S长方形JDCI
=12(y+x+2y)﹣1×(x+y)﹣6(2y﹣5)
=11x+23y+30;
(2)由题意,得
y+x+2y=11,
∴x+3y=11,
由(1)知:2x+y=7,
∴,
解方程得,
将x=2,y=3代入验证,为此方程的解,并符合题意,
∴住房的总面积S=11x+23y+30=11×2+23×3+30=121(平方米),
答:住房的总面积是121平方米;
(3)①由题意,得=,
解得2y=3x,得y=,代入(1)的2x+y=7,
得2x+=7,
解得x=2,y=3,
代入原方程符合题意,
答:x,y的值为2,3;
②根据题意,得
铺设主卧次卧和书房需要木地板:35+5y=35+15=50(m2),
铺设其他区域需要地砖:121﹣50=71(m2),
∴A种活动方案所需的费用:50×500×0.8+71×400×0.85+3000=47140(元),
B种活动方案所需的费用:50×500×0.9+71×400×0.9=48060(元),
∵47140<48060,
故小方家应选择A种活动方案,使铺设地面总费用(含材料费及安装费)更低
一.选择题(共17小题)
1.一件校服,按标价的6折出售,售价是x元,这件校服的标价是( )
A.0.6x元 B.元 C.0.4x元 D.元
2.香蕉的单价为a元/千克,苹果的单价为b元/千克,买2千克苹果和3千克香蕉共需( )元.
A.a+b B.3a+2b C.2a+3b D.5(a+b)
3.笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔记本,2支圆珠笔;小明买4本笔记本,3支圆珠笔.买这些笔记本和圆珠笔,小红和小明一共花( )元.
A.7x+5y B.6x+6y C.5x+7y D.7x+6y
4.在△ABC中,∠C=90°,D是边BC上一点,连接AD,若∠BAD+3∠CAD=90°,DC=a,BD=b,则AB为( )(用含a,b的式子表示)
A.2a+b B.2b+a C.3b+a D.3a+b
5.某药厂计划对售价为m元的药品进行降价销售,现在有三种方案.方案一:第一次降价10%,第二次降价30%;方案二:第一次降价20%,第二次降价15%;方案三:第一、二次降价均为20%.三种方案哪种降价最多( )
A.方案一 B.方案二 C.方案三 D.不能确定
6.疫情期间因口罩需求急速增长导致生产口罩的原材料价格不断上涨,甲、乙、丙三家药店对同一款售价相同的口罩提价销售:甲药店提价20%销售;乙药店提价15%后再提价5%;丙药店提价10%后再提价10%.若顾客想要购买该口罩,选择最划算的商店是( )
A.甲 B.乙 C.丙 D.都一样
7.苹果打8折后价格是p元/千克,则原价是( )
A.1.25p元/千克 B.p元/千克
C.0.8p元/千克 D.0.2p元/千克
8.某药店在甲工厂以每包a元的价格买进了41盒口罩,又在乙工厂以每包b元(a<b)的价格买进了同样的59盒口罩.如果以每包元的价格全部卖出这种口罩,那么这家药店( )
A.亏损了 B.盈利了
C.不盈不亏 D.盈亏不能确定
9.一个长方形的花园长为a,宽为b,如果长增加x,那么新的花园面积为( )
A.a(b+x) B.b(a+x) C.ab+x D.a+bx
10.笔记本的单价是m元,钢笔的单价是n元,甲买3本笔记本和2支钢笔,乙买4本笔记本和3支钢笔,买这些笔记本和钢笔,甲和乙一共花了多少元?( )
A.7m+5n B.5m+7n C.6m+6n D.7n+5m
11.一个两位数,十位数字是a,十位数字比个位数字小2,这个两位数是( )
A.a(a+2) B.10a(a+2) C.10a+(a+2) D.10a+(a﹣2)
12.东西湖区域出租汽车行驶2千米以内(包括2千米)的车费是10元,以后每行驶1千米,再加0.7元.如果某人坐出租汽车行驶了m千米(m是整数,且m≥2),则车费是( )
A.(10﹣0.7m)元 B.(11.4+0.7m)元
C.(8.6+0.7m)元 D.(10+0.7m)元
13.一条河的水流速度是2.5km/h,某船在静水中的速度是vkm/h,则该船在这条河中逆流行驶的速度是( )
A.(v+2.5)km/h B.(v﹣2.5)km/h
C.(v+5)km/h D.(v﹣5)km/h
14.如图,三角尺(阴影部分)的面积为( )
A.ab﹣2πr B. C.ab﹣πr2 D.
15.某淘宝店家为迎接“双十一”抢购活动,在甲批发市场以每件a元的价格进了40件童装,又在乙批发市场以每件b元(a>b)的价格进了同样的60件童装.如果店家以每件元的价格卖出这款童装,卖完后,这家商店( )
A.盈利了 B.亏损了
C.不赢不亏 D.盈亏不能确定
16.有18米长的木材,要做成一个如图的窗框.如果假设窗框横档的长度为x米,那么窗框的面积是( )
A.x(9﹣x)米2 B.x(18﹣2x)米2
C.x(9﹣3x)米2 D.米2
17.已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成( )
A.10b+a B.ba C.100b+a D.b+10a
二.填空题(共9小题)
18.一条河的水流速度是2km/h,轮船在静水中的速度是vkm/h,用式子表示船在这条河中逆水行驶t小时的路程是 km.
19.如图,(图中长度单位:m),钢管的体积是 m3.
20.两船从同一港口同时出发反向而行,甲船顺水航行了6小时,乙船逆水航行了3小时,两船在静水中的速度都是50km/h,水流速度是akm/h,则两船一共航行了 km.(用含a的式子表示)
21.一个两位数M的个位上的数是a,十位上的数是b,把这个两位数的十位上的数与个位上的数交换位置,所得的新数记为N,则M﹣N= .(用含a、b的式子表示)
22.一个两位数的个位上的数是2,十位上的数是x,用含有x的多项式表示这个两位数为 .
23.某种商品原价是m元,第一次降价打“九折”,第二次降价每件又减20元,第二次降价后的售价是 元.
24.一种商品每件成本是a元,原来按成本增加20%定出价格进销售,一段时间后,由于库存积压减价,按原价的9折出售,则现在每件售价为 元.
25.把六张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为20cm,宽为16cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是 .
26.某公园的成人单价是10元,儿童单价是4元.某旅行团有a名成人和b名儿童;旅行团的门票费用总和为 元.
三.解答题(共2小题)
27.已知四个数a、b、c、d(a<b<c<d),满足|a﹣b|+|c﹣d|=|a﹣d|(n≥3,且为整数).
(1)当n=3时,
①若d﹣a=9,求c﹣b的值;
②对于有理数p,满足|b﹣p|=|a﹣d|,请用含b、c的代数式表示p;
(2)若p=|b﹣c|,q=|a﹣d|,且|p﹣q|=|a﹣d|,求n的值.
28.某住房户型平面图如下(单位:米),其中,主卧和次卧的面积一共是35m2.现准备铺设地面,主卧次卧和书房铺设木地板,其他区域铺设地砖.
(1)用含x,y的整式表示住房的总面积,直接写出化简后的结果;
(2)若房子右边的宽AB是11m,住房的总面积是多少平方米?
(3)按市场价格,木地板单价为500元/平方米,地砖单价为400元方米,装修公司有A、B两种活动方案,如表:
活动方案 木地板价格 地砖价格 总安装费
A 8折 8.5折 3000元
B 9折 9折 免收
若主卧和次卧的面积之比为4:3.
①直接写出x,y的值;
②选择哪种活动方案,设地面总费用(含材料费及安装费)更低?
参考答案
一.选择题(共17小题)
1.解:x=标价×0.6;
所以,标价=元.
故选:B.
2.解:根据题意得:买2千克苹果和3千克香蕉共需(3a+2b)元,
故选:B.
3.解:小红花的钱为:3x+2y,
小明花的钱为:4x+3y,
则总共花费为:3x+2y+4x+3y=7x+5y.
故选:A.
4.解:如图,延长BC到E,使CE=CD=a,连接AE.
∵∠ACB=90°,
∴∠CAB+∠B=90°,AC⊥CD,
∵∠BAD+3∠CAD=90°,∠BAD+∠CAD=∠BAC,
∴∠B=2∠CAD.
∵CE=CD,AC⊥CD,
∴AE=AD,即△AED是等腰三角形,
∴∠EAC=∠CAD,
∴∠EAD=2∠CAD=∠B,
∴∠EAB=∠B+∠BAD,
∵∠E=∠ADE=∠B+∠BAD,
∴∠E=∠EAB,
∴AB=EB,
∵EB=EC+CD+BD=a+a+b=2a+b,
∴AB=EB=2a+b.
故选:A.
5.解:方案一:m﹣(1﹣10%)(1﹣30%)m=m﹣63%m=37%m,
方案二:m﹣(1﹣20%)(1﹣15%)m=m﹣68%m=32%m,
方案三:m﹣(1﹣20%)(1﹣20%)m=m﹣64%m=36%m,
∵m>0,
∴37%m>36%m>32%m,
∴方案一降价最多.
故选:A.
6.解:可设同一款售价相同的口罩售价为x元,则
甲药店价格为:(1+20%)=1.2x元;
乙药店价格为:(1+15%)(1+5%)x=1.2075x元;
丙药店价格为:(1+10%)(1+10%)x=1.21x元.
故最划算的商店是甲.
故选:A.
7.解:设苹果的原价为x元,则0.8x=p,
∴x=p÷0.8=1.25p(元/千克),
故选:A.
8.解:∵a<b,
∴(41+59)×﹣(41a+59b)
=50a+50b﹣41a﹣59b
=9a﹣9b
=9(a﹣b)<0,
∴这家药店亏损了.
故选:A.
9.解:长增加x,则长为x+a,面积为:b(a+x),
故选:B.
10.解:甲花的钱为:(3m+2n)元,
乙花的钱为:(4m+3n)元,
则甲和乙一共花费为:3m+2n+4m+3n=(7m+5n)元.
故选:A.
11.解:∵一个两位数,十位数字是a,十位数字比个位数字小2,
∴这个两位数是:10a+(a+2).
故选:C.
12.解:由题意可得,
车费是:10+(m﹣2)×0.7=(0.7m+8.6)元,
故选:C.
13.解集:因为船的逆流速度=船在静水中的速度﹣水流速度,
即船的逆流速度是(v﹣2.5)km/h.
故选:B.
14.解集:阴影部分的面积为:S△﹣S圆=ab﹣πr2,
故选:D.
15.解:根据题意列得:在甲批发市场童装的利润为40(﹣a)=20(a+b)﹣40a=20a﹣20b;
在乙批发市场童装的利润为60(﹣b)=30(a+b)﹣60b=30a﹣30b,
∴该商店的总利润为20b﹣20a+30a﹣30b=10a﹣10b=10(a﹣b),
∵a>b,∴a﹣b>0,即10(a﹣b)>0,
则这家商店盈利了.
故选:A.
16.解:结合图形,显然窗框的另一边是 =9﹣x(米).
根据长方形的面积公式,得:窗框的面积是x(9﹣x)平方米.
故选:D.
17.解:两位数的表示方法:十位数字×10+个位数字;三位数字的表示方法:百位数字×100+十位数字×10+个位数字.
a是两位数,b是一位数,依据题意可得b扩大了100倍,所以这个三位数可表示成100b+a.
故选:C.
二.填空题(共9小题)
18.解:船在这条河中逆水行驶t小时的路程是t(v﹣2)km.
故答案为:t(v﹣2).
19.解:外圆柱的体积是:πR2acm3,
内圆柱的体积是:πr2acm3,
钢管的体积是:(πR2a﹣πr2a)cm3.
故答案为:(πR2a﹣πr2a).
20.解:∵甲船顺水航行了6小时,乙船逆水行了3小时,两船在静水中的速度都是50km/h,水流速度是akm/h,
∴甲船顺水的速度是:(50+a)km/h,乙船逆水的速度是:(50﹣a)km/h,
∴两船一共航行了:6(50+a)+3(50﹣a)=300+6a+150﹣3a=(450+3a)km.
答:两船一共航行了(450+3a)千米.
故答案为:(450+3a).
21.解:由题意可得:M=10b+a,N=10a+b,
M﹣N=10b+a﹣(10a+b)
=9b﹣9a.
故答案为:9b﹣9a.
22.解:∵一个两位数的个位上的数是2,十位上的数是x,
∴这个两位数为10x+2.
故答案为:10x+2.
23.解:根据题意得:
第一次降价后的售价是0.9m,第二次降价后的售价是(0.9m﹣20)元.
故答案为:(0.9m﹣20).
24.解:∵每件成本a元,原来按成本增加20%定出价格,
∴每件售价为(1+20%)a=1.2a(元);
现在售价:1.2a×90%=1.08a(元);
故答案是:1.08a.
25.解:设小长方形长为xcm,宽为ycm,由题意得:x+3y=20,
阴影部分周长的和是:20×2+(16﹣3y+16﹣x)×2=104﹣6y﹣2x=104﹣2(3y+x)=104﹣40=64(cm),
故答案为:64cm.
26.解:由题意得:10a+4b,
故答案为:(10a+4b).
三.解答题(共2小题)
27.解:(1)①∵n=3,
∴|a﹣b|+|c﹣d|=|a﹣d|,
∵a<b<c<d,
∴b﹣a+d﹣c=(d﹣a),
∴c﹣b=(d﹣a),
∵d﹣a=9,
∴c﹣b=6;
②∵|b﹣p|=|a﹣d|,
∴b﹣p=±(d﹣a),
∵d﹣a=(c﹣b),
∴b﹣p=±×(c﹣b)=±2(c﹣b),
∴p=2c﹣b或3b﹣2c;
(2)∵|a﹣b|+|c﹣d|=|a﹣d|,a<b<c<d,
∴c﹣b=(1﹣)(d﹣a),
∵p=|b﹣c|,q=|a﹣d|,且|p﹣q|=|a﹣d|,
∴||(1﹣)(d﹣a)|﹣|a﹣d||>|a﹣d|,
∴|a﹣d|>|a﹣d|,
∴2n<12,
∴n<6,
∵n≥3且为正整数,
∴n的值是3或4或5.
28.解:(1)如图,延长BC,HG交于点I,延长DE交HI于点J,
∵住房的总面积S=S长方形ABIH﹣S长方形GFEJ﹣S长方形JDCI,
∵主卧和次卧的面积一共是35m2.
∴5(2x+y)=35,
∴2x+y=7,
∴AH=7+5=12,
∴IC=BI﹣BC=AH﹣BC=12﹣6=6,
∴JE=JD﹣DE=IC﹣DE=6﹣5=1,
∵JI=AB﹣HG﹣EF=y+x+2y﹣5﹣(x+y)=2y﹣5,
∴住房的总面积S=S长方形ABIH﹣S长方形GFEJ﹣S长方形JDCI
=12(y+x+2y)﹣1×(x+y)﹣6(2y﹣5)
=11x+23y+30;
(2)由题意,得
y+x+2y=11,
∴x+3y=11,
由(1)知:2x+y=7,
∴,
解方程得,
将x=2,y=3代入验证,为此方程的解,并符合题意,
∴住房的总面积S=11x+23y+30=11×2+23×3+30=121(平方米),
答:住房的总面积是121平方米;
(3)①由题意,得=,
解得2y=3x,得y=,代入(1)的2x+y=7,
得2x+=7,
解得x=2,y=3,
代入原方程符合题意,
答:x,y的值为2,3;
②根据题意,得
铺设主卧次卧和书房需要木地板:35+5y=35+15=50(m2),
铺设其他区域需要地砖:121﹣50=71(m2),
∴A种活动方案所需的费用:50×500×0.8+71×400×0.85+3000=47140(元),
B种活动方案所需的费用:50×500×0.9+71×400×0.9=48060(元),
∵47140<48060,
故小方家应选择A种活动方案,使铺设地面总费用(含材料费及安装费)更低
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
