2021-2022学年浙教新版八年级上册数学《第1章 三角形的初步认识》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年浙教新版八年级上册数学《第1章 三角形的初步认识》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 302.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-08 19:48:10 | ||
图片预览

文档简介
2021-2022学年浙教新版八年级上册数学《第1章
三角形的初步认识》单元测试卷
一.选择题
1.下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
A.
B.
C.
D.
2.如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确
B.①、②都不正确
C.①正确②不正确
D.①不正确,②正确
3.如图,在正方形ABCD中,BD=2,∠DCE是正方形ABCD的外角,P是∠DCE的角平分线CF上任意一点,则△PBD的面积等于( )
A.1
B.1.5
C.2
D.2.5
4.下列各组线段组成一个三角形的是( )
A.4cm,6cm,11cm
B.3cm,4cm,5cm
C.4cm,5cm,1cm
D.2cm,3cm,6cm
5.在△ABC中,∠A﹣∠C=∠B,那么△ABC是( )
A.等边三角形
B.锐角三角形
C.钝角三角形
D.直角三角形
6.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )
A.90°
B.110°
C.100°
D.120°
7.下列图形中,和所给图全等的图形是( )
A.
B.
C.
D.
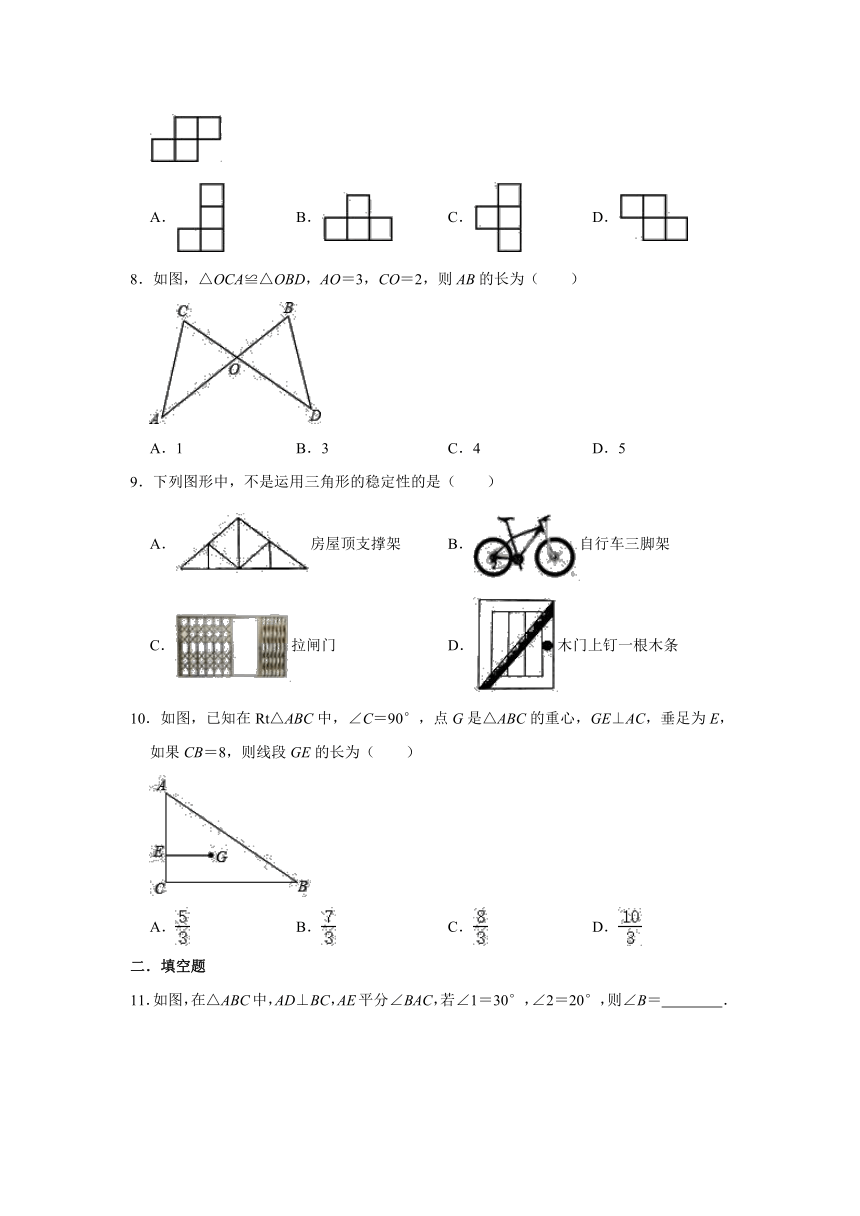
8.如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )
A.1
B.3
C.4
D.5
9.下列图形中,不是运用三角形的稳定性的是( )
A.房屋顶支撑架
B.自行车三脚架
C.拉闸门
D.木门上钉一根木条
10.如图,已知在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E,如果CB=8,则线段GE的长为( )
A.
B.
C.
D.
二.填空题
11.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=
.
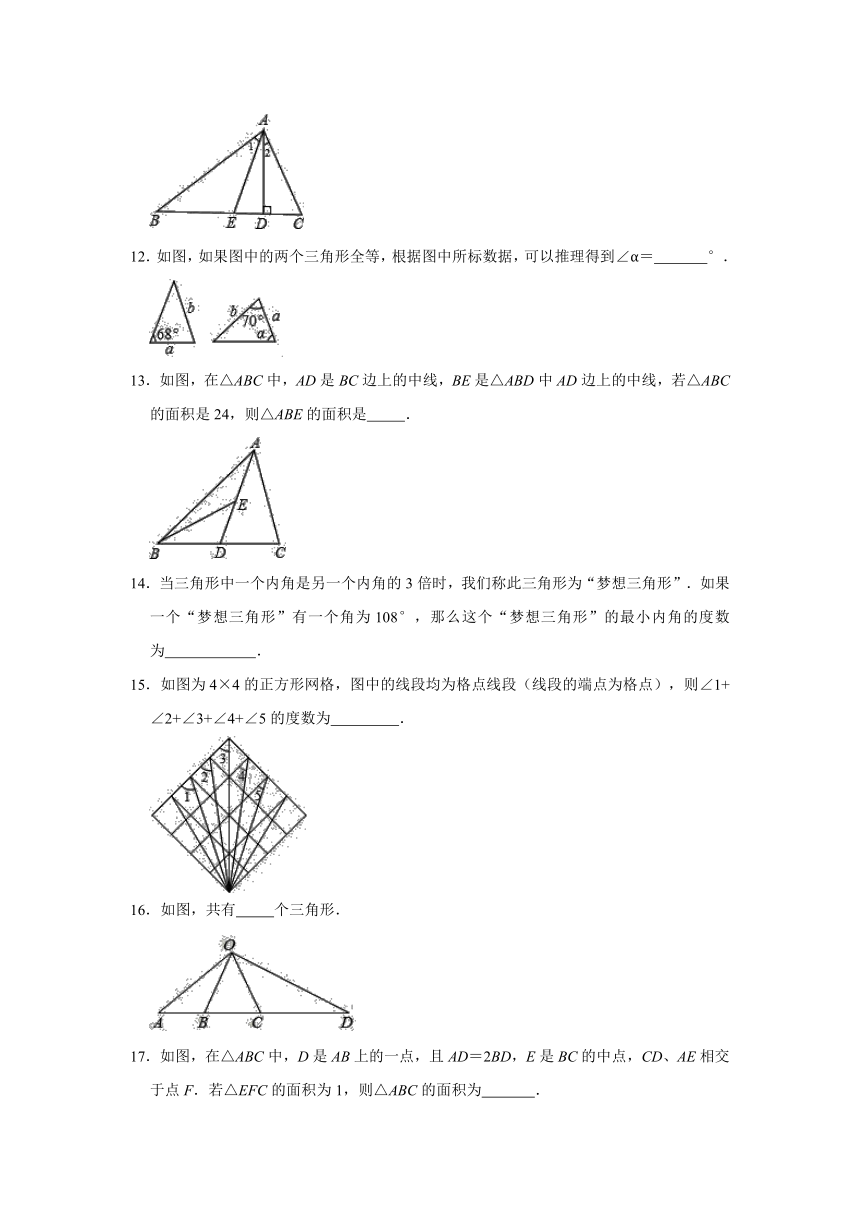
12.如图,如果图中的两个三角形全等,根据图中所标数据,可以推理得到∠α=
°.
13.如图,在△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是
.
14.当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为
.
15.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为
.
16.如图,共有
个三角形.
17.如图,在△ABC中,D是AB上的一点,且AD=2BD,E是BC的中点,CD、AE相交于点F.若△EFC的面积为1,则△ABC的面积为
.
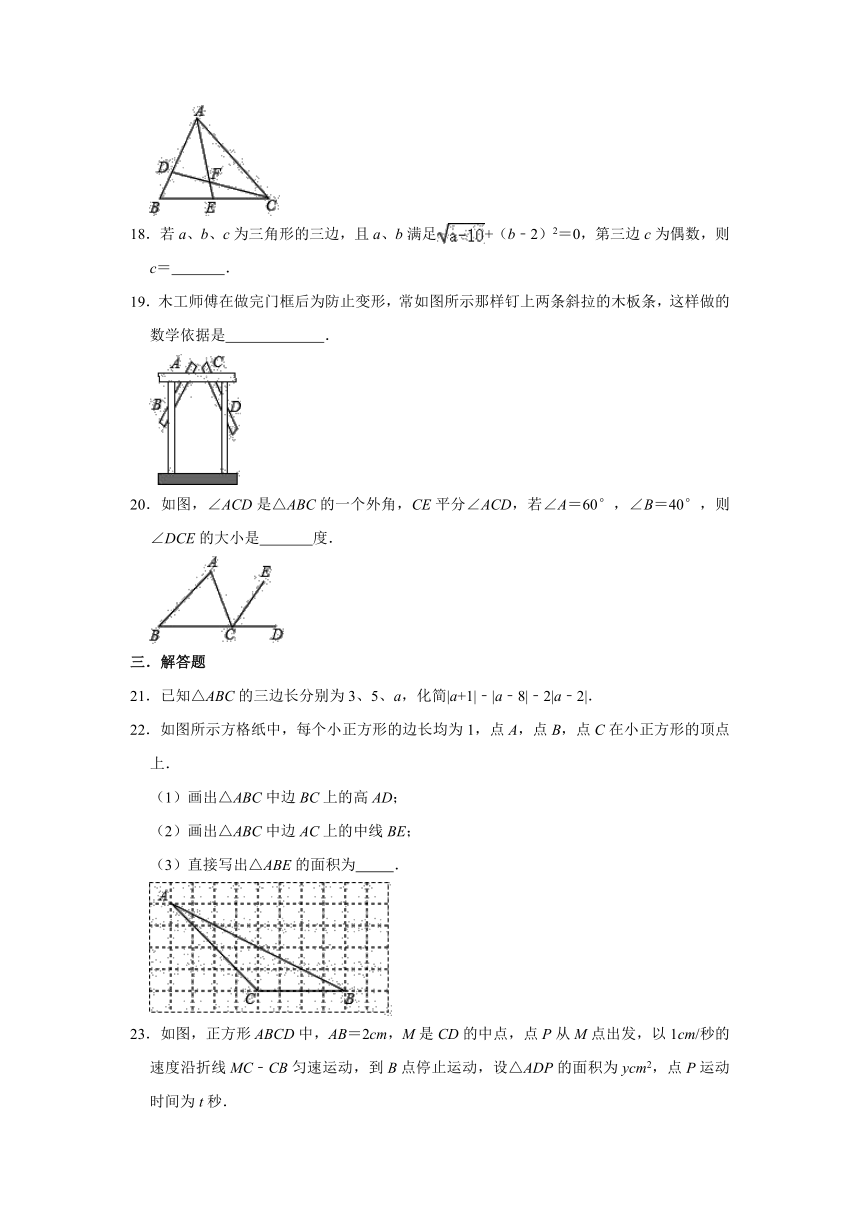
18.若a、b、c为三角形的三边,且a、b满足+(b﹣2)2=0,第三边c为偶数,则c=
.
19.木工师傅在做完门框后为防止变形,常如图所示那样钉上两条斜拉的木板条,这样做的数学依据是
.
20.如图,∠ACD是△ABC的一个外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠DCE的大小是
度.
三.解答题
21.已知△ABC的三边长分别为3、5、a,化简|a+1|﹣|a﹣8|﹣2|a﹣2|.
22.如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为
.
23.如图,正方形ABCD中,AB=2cm,M是CD的中点,点P从M点出发,以1cm/秒的速度沿折线MC﹣CB匀速运动,到B点停止运动,设△ADP的面积为ycm2,点P运动时间为t秒.
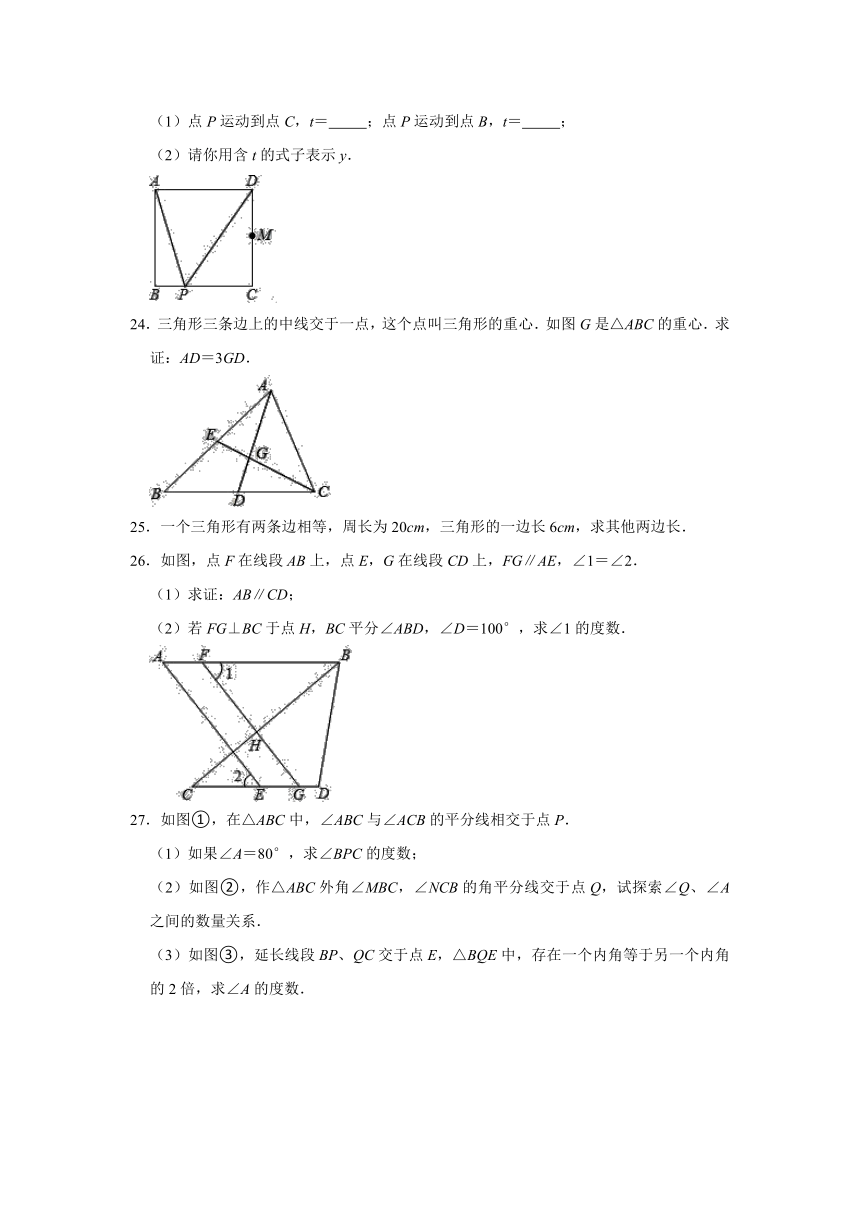
(1)点P运动到点C,t=
;点P运动到点B,t=
;
(2)请你用含t的式子表示y.
24.三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是△ABC的重心.求证:AD=3GD.
25.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
26.如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2.
(1)求证:AB∥CD;
(2)若FG⊥BC于点H,BC平分∠ABD,∠D=100°,求∠1的度数.
27.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案与试题解析
一.选择题
1.解:A、知道两个角,可以计算出第三个角的度数,因此可以判断出三角形类型;
B、露出的角是钝角,因此是钝角三角形;
C、露出的角是锐角,其他两角都不知道,因此不能判断出三角形类型;
D、露出的角是钝角,因此是钝角三角形;
故选:C.
2.解:AD是三角形ABC的角平分线,
则是∠BAC的角平分线,
所以AO是△ABE的角平分线,故①正确;
BE是三角形ABC的中线,
则E是AC是中点,而O不一定是AD的中点,故②错误.
故选:C.
3.解:过C点作CG⊥BD于G,
∵CF是∠DCE的平分线,
∴∠FCE=45°,
∵∠DBC=45°,
∴CF∥BD,
∴CG等于△PBD的高,
∵BD=2,
∴CG=1,
△PBD的面积等于=1.故选A.
4.解:A、4+6<11,不能组成三角形;
B、3+4>5,能组成三角形;
C、1+4=5,不能够组成三角形;
D、2+3<6,不能组成三角形.
故选:B.
5.解:∵∠A+∠B+∠C=180°,
∴∠C+∠B=180°﹣∠A,
而∠A﹣∠C=∠B,
∴∠C+∠B=∠A,
∴180°﹣∠A=∠A,解得∠A=90°,
∴△ABC为直角三角形.
故选:D.
6.解:设三个外角的度数分别为2k,3k,4k,
根据三角形外角和定理,可知2k°+3k°+4k°=360°,得k=40°,
所以最小的外角为2k=80°,
故最大的内角为180°﹣80°=100°.
故选:C.
7.解;如图所示:和左图全等的图形是选项D.
故选:D.
8.解:∵△OCA≌△OBD,
∴CO=BO=2,
∴AB=AO+BO=2+3=5,
故选:D.
9.解:伸缩的拉闸门是利用了四边形的不稳定性,A、B、D都是利用了三角形的稳定性,
故选:C.
10.解:延长AG交BC于D,如图,
∵点G是△ABC的重心,
∴CD=BD=BC=4,AG=2GD,
∵GE⊥AC,
∴∠AEG=90°,
而∠C=90°,
∴GE∥CD,
∴△AEG∽△ACD,
∴===,
∴EG=CD=×4=.
故选:C.
二.填空题
11.解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD
=90°﹣30°﹣10°=50°.
故答案为50°.
12.解:∵图中的两个三角形全等,
∴∠α=68°.
故答案为68.
13.解:∵AD是△ABC的中线,
∴S△ABD=S△ABC=12.
∵CE是△ABD的中线,
∴S△ABE=S△ABD=6.
故答案为:6
14.解:当108°的角是另一个内角的3倍时,最小角为180°﹣108°﹣108÷3°=36°,
当180°﹣108°=72°的角是另一个内角的3倍时,最小角为72°÷(1+3)=18°,
因此,这个“梦想三角形”的最小内角的度数为36°或18°.
故答案为:18°或36°.
15.解:在图中标上字母,如图所示.
∵四边形ABCD为4×4的正方形,
∴∠3=45°.
∵四边形ANPE为1×1的正方形,
∴AE=AN.
∵四边形CDEF和四边形BCMN均为4×3的长方形,
∴CE=CN.
在△ACE和△ACN中,,
∴△ACE≌△ACN(SSS),
∴∠AEC=∠ANC,
∴∠2+∠4+90°=180°,
∴∠2与∠4互余.
同理可得:∠1与∠5互余.
∴∠1+∠2+∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)+∠3=90°+90°+45°=225°.
故答案为:225°.
16.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
17.解:连接BF,如图,
∵AE为中线,
∴S△ABE=S△ACE,S△BEF=S△CEF=1,
∴S△ABF=S△ACF,
设△BDF的面积为S,则△ADF的面积为2S,△ACF的面积为3S,
∵S△ADC=2S△BCD,
∴2S+3S=2(S+1+1),解得S=,
∴△ABC的面积=2S+3S+S+1+1=6S+2=6×+2=10.
故答案为10.
18.解:∵a、b满足+(b﹣2)2=0,
∴a=10,b=2,
∵a、b、c为三角形的三边,
∴8<c<12,
∵第三边c为偶数,
∴c=10.
故答案为:10.
19.解:木工师傅在做完门框后为防止变形,常如图所示那样钉上两条斜拉的木板条,这样做的数学依据是三角形具有稳定性,
故答案为:三角形具有稳定性.
20.解:∵∠ACD是△ABC的一个外角,∠A=60°,∠B=40°,
∴∠ACD=60°+40°=100°,
∵CE平分∠ACD,
∴∠ACE=∠ECD=50°,
故答案为:50.
三.解答题
21.解:∵△ABC的三边长分别为3、5、a,
∴5﹣3<a<3+5,
解得:2<a<8,
故|a+1|﹣|a﹣8|﹣2|a﹣2|
=a+1﹣(8﹣a)﹣2(a﹣2)
=a+1﹣8+a﹣2a+4
=﹣3.
22.解:(1)如图所示,线段AD即为所求;
(2)如图所示,线段BE即为所求;
(3)S△ABC=BC?AD=4×4=8.
∴△ABE的面积=S△ABC=4,
故答案为:4.
23.解:(1)∵正方形ABCD中,AB=2cm,
∴CD=AB=BC=AD=2cm,
∵M是CD的中点,
∴MC=1cm,
∵点P从M点出发,以1cm/秒的速度沿折线MC﹣CB匀速运动,
∴点P运动到点C,t=1,点P运动到点B,t=3,
故答案为1;3;
(2)设△ADP的面积为ycm2,点P运动时间为t秒,
当P在MC上时,y=?DP==t+1(0≤t<1);
当P在BC上时,y=AD?DC==2(1≤t≤3).
综上,y=.
24.证明:连接DE,
∵点G是△ABC的重心,
∴点E和点D分别是AB和BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC且DE=AC,
∴△DEG∽△ACG,
∴,
∴,
∴,
∴AD=3DG,
即AD=3GD.
25.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
26.(1)证明:∵FG∥AE,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴AB∥CD.
(2)解:∵AB∥CD,
∴∠ABD+∠D=180°,
∵∠D=100°,
∴∠ABD=180°﹣∠D=80°,
∵BC平分∠ABD,
∴∠4=∠ABD=40°,
∵FG⊥BC,
∴∠1+∠4=90°,
∴∠1=90°﹣40°=50°.
27.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°﹣∠ABC﹣∠ACB)
=(180°+∠A)
=90°+∠A
∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
三角形的初步认识》单元测试卷
一.选择题
1.下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
A.
B.
C.
D.
2.如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确
B.①、②都不正确
C.①正确②不正确
D.①不正确,②正确
3.如图,在正方形ABCD中,BD=2,∠DCE是正方形ABCD的外角,P是∠DCE的角平分线CF上任意一点,则△PBD的面积等于( )
A.1
B.1.5
C.2
D.2.5
4.下列各组线段组成一个三角形的是( )
A.4cm,6cm,11cm
B.3cm,4cm,5cm
C.4cm,5cm,1cm
D.2cm,3cm,6cm
5.在△ABC中,∠A﹣∠C=∠B,那么△ABC是( )
A.等边三角形
B.锐角三角形
C.钝角三角形
D.直角三角形
6.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )
A.90°
B.110°
C.100°
D.120°
7.下列图形中,和所给图全等的图形是( )
A.
B.
C.
D.
8.如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )
A.1
B.3
C.4
D.5
9.下列图形中,不是运用三角形的稳定性的是( )
A.房屋顶支撑架
B.自行车三脚架
C.拉闸门
D.木门上钉一根木条
10.如图,已知在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E,如果CB=8,则线段GE的长为( )
A.
B.
C.
D.
二.填空题
11.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=
.
12.如图,如果图中的两个三角形全等,根据图中所标数据,可以推理得到∠α=
°.
13.如图,在△ABC中,AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是24,则△ABE的面积是
.
14.当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为
.
15.如图为4×4的正方形网格,图中的线段均为格点线段(线段的端点为格点),则∠1+∠2+∠3+∠4+∠5的度数为
.
16.如图,共有
个三角形.
17.如图,在△ABC中,D是AB上的一点,且AD=2BD,E是BC的中点,CD、AE相交于点F.若△EFC的面积为1,则△ABC的面积为
.
18.若a、b、c为三角形的三边,且a、b满足+(b﹣2)2=0,第三边c为偶数,则c=
.
19.木工师傅在做完门框后为防止变形,常如图所示那样钉上两条斜拉的木板条,这样做的数学依据是
.
20.如图,∠ACD是△ABC的一个外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠DCE的大小是
度.
三.解答题
21.已知△ABC的三边长分别为3、5、a,化简|a+1|﹣|a﹣8|﹣2|a﹣2|.
22.如图所示方格纸中,每个小正方形的边长均为1,点A,点B,点C在小正方形的顶点上.
(1)画出△ABC中边BC上的高AD;
(2)画出△ABC中边AC上的中线BE;
(3)直接写出△ABE的面积为
.
23.如图,正方形ABCD中,AB=2cm,M是CD的中点,点P从M点出发,以1cm/秒的速度沿折线MC﹣CB匀速运动,到B点停止运动,设△ADP的面积为ycm2,点P运动时间为t秒.
(1)点P运动到点C,t=
;点P运动到点B,t=
;
(2)请你用含t的式子表示y.
24.三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是△ABC的重心.求证:AD=3GD.
25.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
26.如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2.
(1)求证:AB∥CD;
(2)若FG⊥BC于点H,BC平分∠ABD,∠D=100°,求∠1的度数.
27.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案与试题解析
一.选择题
1.解:A、知道两个角,可以计算出第三个角的度数,因此可以判断出三角形类型;
B、露出的角是钝角,因此是钝角三角形;
C、露出的角是锐角,其他两角都不知道,因此不能判断出三角形类型;
D、露出的角是钝角,因此是钝角三角形;
故选:C.
2.解:AD是三角形ABC的角平分线,
则是∠BAC的角平分线,
所以AO是△ABE的角平分线,故①正确;
BE是三角形ABC的中线,
则E是AC是中点,而O不一定是AD的中点,故②错误.
故选:C.
3.解:过C点作CG⊥BD于G,
∵CF是∠DCE的平分线,
∴∠FCE=45°,
∵∠DBC=45°,
∴CF∥BD,
∴CG等于△PBD的高,
∵BD=2,
∴CG=1,
△PBD的面积等于=1.故选A.
4.解:A、4+6<11,不能组成三角形;
B、3+4>5,能组成三角形;
C、1+4=5,不能够组成三角形;
D、2+3<6,不能组成三角形.
故选:B.
5.解:∵∠A+∠B+∠C=180°,
∴∠C+∠B=180°﹣∠A,
而∠A﹣∠C=∠B,
∴∠C+∠B=∠A,
∴180°﹣∠A=∠A,解得∠A=90°,
∴△ABC为直角三角形.
故选:D.
6.解:设三个外角的度数分别为2k,3k,4k,
根据三角形外角和定理,可知2k°+3k°+4k°=360°,得k=40°,
所以最小的外角为2k=80°,
故最大的内角为180°﹣80°=100°.
故选:C.
7.解;如图所示:和左图全等的图形是选项D.
故选:D.
8.解:∵△OCA≌△OBD,
∴CO=BO=2,
∴AB=AO+BO=2+3=5,
故选:D.
9.解:伸缩的拉闸门是利用了四边形的不稳定性,A、B、D都是利用了三角形的稳定性,
故选:C.
10.解:延长AG交BC于D,如图,
∵点G是△ABC的重心,
∴CD=BD=BC=4,AG=2GD,
∵GE⊥AC,
∴∠AEG=90°,
而∠C=90°,
∴GE∥CD,
∴△AEG∽△ACD,
∴===,
∴EG=CD=×4=.
故选:C.
二.填空题
11.解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1﹣∠2=30°﹣20°=10°,
Rt△ABD中,∠B=90°﹣∠BAD
=90°﹣30°﹣10°=50°.
故答案为50°.
12.解:∵图中的两个三角形全等,
∴∠α=68°.
故答案为68.
13.解:∵AD是△ABC的中线,
∴S△ABD=S△ABC=12.
∵CE是△ABD的中线,
∴S△ABE=S△ABD=6.
故答案为:6
14.解:当108°的角是另一个内角的3倍时,最小角为180°﹣108°﹣108÷3°=36°,
当180°﹣108°=72°的角是另一个内角的3倍时,最小角为72°÷(1+3)=18°,
因此,这个“梦想三角形”的最小内角的度数为36°或18°.
故答案为:18°或36°.
15.解:在图中标上字母,如图所示.
∵四边形ABCD为4×4的正方形,
∴∠3=45°.
∵四边形ANPE为1×1的正方形,
∴AE=AN.
∵四边形CDEF和四边形BCMN均为4×3的长方形,
∴CE=CN.
在△ACE和△ACN中,,
∴△ACE≌△ACN(SSS),
∴∠AEC=∠ANC,
∴∠2+∠4+90°=180°,
∴∠2与∠4互余.
同理可得:∠1与∠5互余.
∴∠1+∠2+∠3+∠4+∠5=(∠1+∠5)+(∠2+∠4)+∠3=90°+90°+45°=225°.
故答案为:225°.
16.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
17.解:连接BF,如图,
∵AE为中线,
∴S△ABE=S△ACE,S△BEF=S△CEF=1,
∴S△ABF=S△ACF,
设△BDF的面积为S,则△ADF的面积为2S,△ACF的面积为3S,
∵S△ADC=2S△BCD,
∴2S+3S=2(S+1+1),解得S=,
∴△ABC的面积=2S+3S+S+1+1=6S+2=6×+2=10.
故答案为10.
18.解:∵a、b满足+(b﹣2)2=0,
∴a=10,b=2,
∵a、b、c为三角形的三边,
∴8<c<12,
∵第三边c为偶数,
∴c=10.
故答案为:10.
19.解:木工师傅在做完门框后为防止变形,常如图所示那样钉上两条斜拉的木板条,这样做的数学依据是三角形具有稳定性,
故答案为:三角形具有稳定性.
20.解:∵∠ACD是△ABC的一个外角,∠A=60°,∠B=40°,
∴∠ACD=60°+40°=100°,
∵CE平分∠ACD,
∴∠ACE=∠ECD=50°,
故答案为:50.
三.解答题
21.解:∵△ABC的三边长分别为3、5、a,
∴5﹣3<a<3+5,
解得:2<a<8,
故|a+1|﹣|a﹣8|﹣2|a﹣2|
=a+1﹣(8﹣a)﹣2(a﹣2)
=a+1﹣8+a﹣2a+4
=﹣3.
22.解:(1)如图所示,线段AD即为所求;
(2)如图所示,线段BE即为所求;
(3)S△ABC=BC?AD=4×4=8.
∴△ABE的面积=S△ABC=4,
故答案为:4.
23.解:(1)∵正方形ABCD中,AB=2cm,
∴CD=AB=BC=AD=2cm,
∵M是CD的中点,
∴MC=1cm,
∵点P从M点出发,以1cm/秒的速度沿折线MC﹣CB匀速运动,
∴点P运动到点C,t=1,点P运动到点B,t=3,
故答案为1;3;
(2)设△ADP的面积为ycm2,点P运动时间为t秒,
当P在MC上时,y=?DP==t+1(0≤t<1);
当P在BC上时,y=AD?DC==2(1≤t≤3).
综上,y=.
24.证明:连接DE,
∵点G是△ABC的重心,
∴点E和点D分别是AB和BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC且DE=AC,
∴△DEG∽△ACG,
∴,
∴,
∴,
∴AD=3DG,
即AD=3GD.
25.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
26.(1)证明:∵FG∥AE,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴AB∥CD.
(2)解:∵AB∥CD,
∴∠ABD+∠D=180°,
∵∠D=100°,
∴∠ABD=180°﹣∠D=80°,
∵BC平分∠ABD,
∴∠4=∠ABD=40°,
∵FG⊥BC,
∴∠1+∠4=90°,
∴∠1=90°﹣40°=50°.
27.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°﹣∠ABC﹣∠ACB)
=(180°+∠A)
=90°+∠A
∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
