5.5 平行四边形的判定

(共16张PPT)
平行四边形有哪些性质？
1.边:
2.角:
3. 对角线:
平行四边形两组对边分别平行.
平行四边形两组对边分别相等.
平行四边形两组对角分别相等.
平行四边形对角线互相平分.
温故知新
5.5 平行四边形的判定
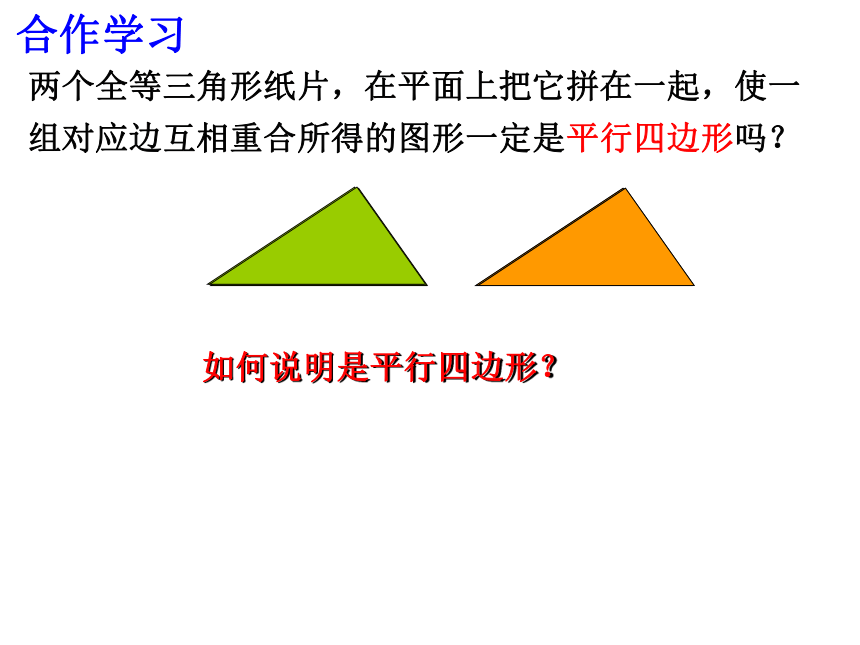
两个全等三角形纸片，在平面上把它拼在一起，使一
组对应边互相重合所得的图形一定是平行四边形吗？
如何说明是平行四边形？
合作学习
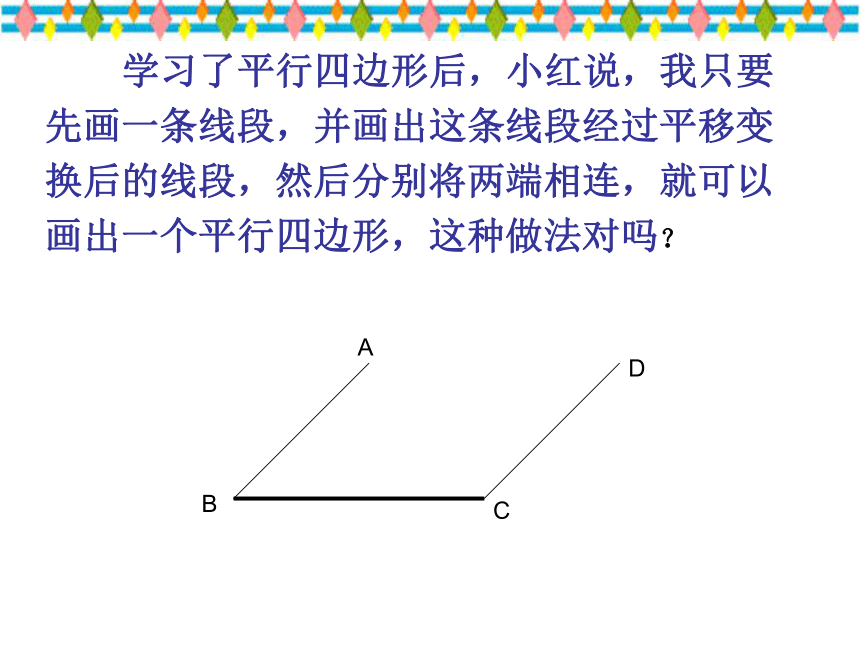
学行四边形后，小红说，我只要先画一条线段，并画出这条线段经过平移变换后的线段，然后分别将两端相连，就可以画出一个平行四边形，这种做法对吗？
A
B
C
D
证明:如图,连接BD.
∵AD∥BC
∴∠ADB=∠CBD（两直线平行，内错角相等）
又∵AD=BC,BD=BD
∴△ADB≌△CBD (SAS)
∴∠ABD=∠CDB（全等三角形的对应角相等）
∴AB∥DC（内错角相等，两直线平行）
∴四边形ABCD是平行四边形（两组对边分别平行的四边形是平行四边形）
A
B
C
D
一组对边平行且相等的四边形是平行四边形。
已知：在四边形ABCD中，AD＝BC，AD∥BC。
求证：四边形ABCD是平行四边形。
AD // BC
=
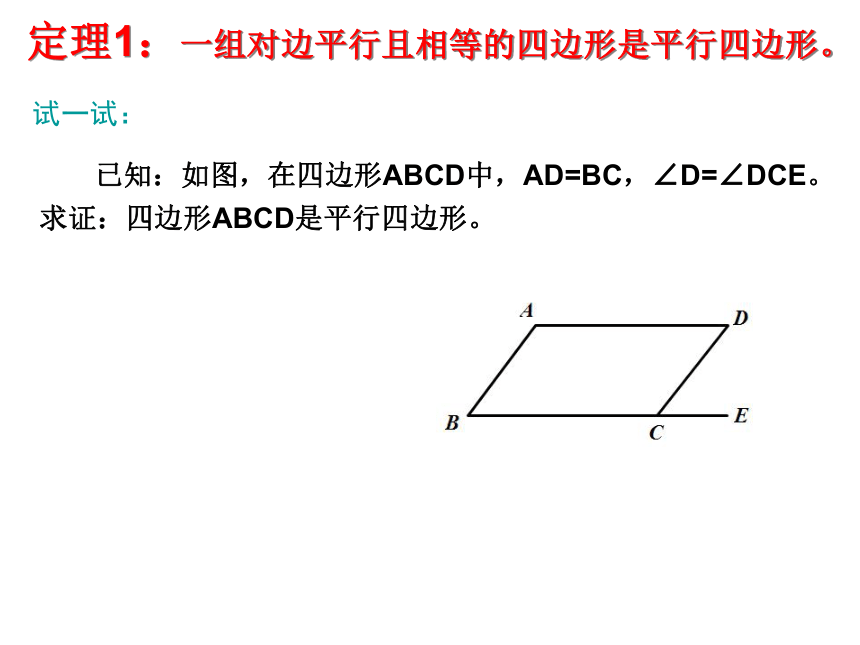
定理1：一组对边平行且相等的四边形是平行四边形。
试一试：
已知：如图，在四边形ABCD中，AD=BC，∠D=∠DCE。求证：四边形ABCD是平行四边形。
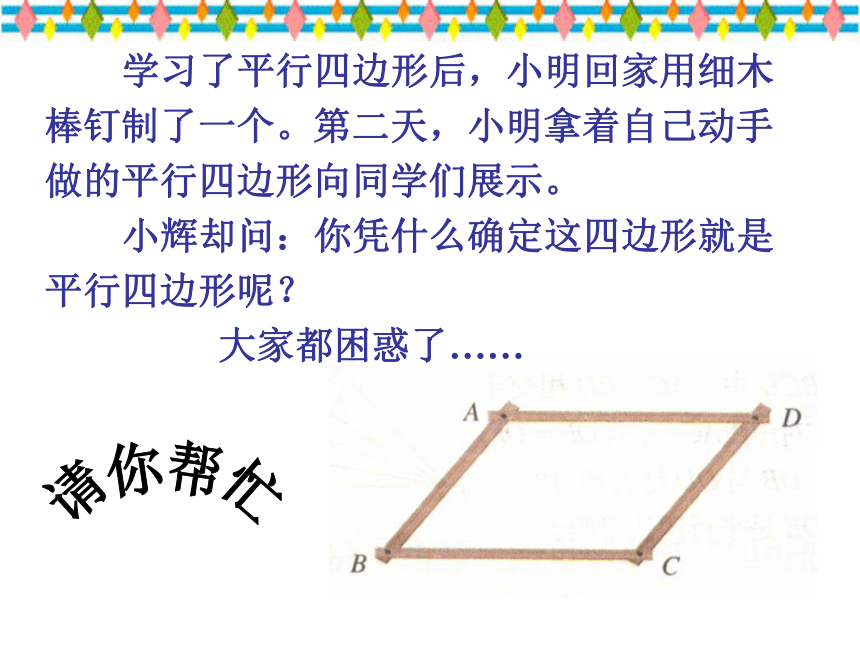
学行四边形后，小明回家用细木棒钉制了一个。第二天，小明拿着自己动手做的平行四边形向同学们展示。
小辉却问：你凭什么确定这四边形就是平行四边形呢？
大家都困惑了……
B
C
A
D
小明提出：只要测得AB=CD，AD=BC
就可以断定ABCD就是平行四边形。
已知AD=BC，AB=CD，求证:四边形ABCD是平行四边形
（内错角相等，两直线平行）
(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形
证明：如图，连结AC，
∵ AB=CD，AD=BC （已知）
又∵ AC=AC （公共边）
∴△ABC≌△CDA（SSS）
∴∠BAC=∠DCA，∠DAC=∠BCA
∴ AB∥CD，AD∥BC
∴四边形ABCD是平行四边形
C
B
D
A
（全等三角形的对应角相等）
1.AB=CD，AB∥CD （ ）
2.AB=CD，AD=BC （ ）
3.AB=BC，AD=DC （ ）
4.AB ∥ CD，AD ∥ BC （ ）
5.AB ∥ CD，AD=BC （ ）
6.∠A+∠B=180°,AD=BC ( )
定理2：两组对边分别相等的四边形是平行四边形
定理1：一组对边平行且相等的四边形是平行四边形
定义：两组对边分别平行 的四边形是平行四边形
满足下列条件的四边形ABCD是不是平行四边形，若是，在括号内打“√”，若不是，则打“×”。
√
√
√
×
×
√
A
B
C
D
A
B
C
D
定理2：两组对边分别相等的四边形是平行四边形
定理1：一组对边平行且相等的四边形是平行四边形
定义：两组对边分别平行 的四边形是平行四边形
例1：已知，如图，在 ABCD中，点E、F
分别是边AB、CD的中点。 求证：EF//AD//BC
A
B
C
D
E
F
定理2：两组对边分别相等的四边形是平行四边形
定理1：一组对边平行且相等的四边形是平行四边形
定义：两组对边分别平行 的四边形是平行四边形
试一试：
已知：如图，E,F分别是平行四边形ABCD 的边AD,BC的中点。求证：BE=DF.
D
F
E
C
B
A
定理2：两组对边分别相等的四边形是平行四边形
定理1：一组对边平行且相等的四边形是平行四边形
定义：两组对边分别平行 的四边形是平行四边形
试一试：
已知：四边形ABCD和AEFD都是平行四边形
求证：四边形BCFE是平行四边形
A
E
B
C
D
F
定理2：两组对边分别相等的四边形是平行四边形
定理1：一组对边平行且相等的四边形是平行四边形
定义：两组对边分别平行 的四边形是平行四边形
例2、已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF。
求证：四边形BFDE是平行四边形
D
A
B
C
E
F
定理2：两组对边分别相等的四边形是平行四边形
定理1：一组对边平行且相等的四边形是平行四边形
定义：两组对边分别平行 的四边形是平行四边形
如图，在平行四边形ABCD中，E、F、G、H分别是各边上的点，且AE=CG，AH=CF，
求证：四边形EFGH是平行四边形。
书本最后一题