1.5 三角形全等的判定 同步练习(含解析)
文档属性
| 名称 | 1.5 三角形全等的判定 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 11:31:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学浙教版八年级上册1.5 三角形全等的判定 同步练习
一、单选题
1.如图,在 和 中, ,添加一个条件,不能证明 和 全等的是(?? )
A.????????????????????B.????????????????????C.????????????????????D.?
2.如图,B、E、C、F在同一直线上,BE=CF,AB∥DE,请你添加一个合适的条件,使△ABC≌△DEF,其中不符合三角形全等的条件是(?? )
A.?AC=DF???????????????????????????B.?AB=DE???????????????????????????C.?∠A=∠D???????????????????????????D.?∠ACB=∠F
3.如图,用尺规作图作∠BAC的平分线AD , 第一步是以A为圆心,任意长为半径画弧,分别交AB , AC于点E , F;第二步是分别以E , F为圆心,以大于 EF长为半径画弧,两圆弧交于D点,连接AD , AD即为所求作,请说明△AFD≌△AED的依据是(??? )
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?AAS
4.如图,在 中, ,按以下步骤作图:①以点 为圆心,以小于 的长为半径作弧,分别交 , 于点 , ;②分别以点 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;③连接 ,交 于点 .若 , ,则 的长为(?? )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
5.如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是(? )
A.?∠ABC=∠ABD??????????????????B.?∠BAC=∠BAD??????????????????????C.?AC=AD??????????????????????D.?AC=BC
6.下列判定两个等腰三角形全等的方法中,正确的是(? )
A.?顶角对应相等????????????B.?底边对应相等????????????????C.?两腰对应相等????????????D.?一腰和底边对应相等
7.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件错误的是(? )
A.?BC=DC,∠A=∠D????????????????????????????????????????????B.?BC=EC,AC=DC
C.?∠B=∠E,∠BCE=∠ACD????????????????????????????????????D.?BC=EC,∠B=∠E
8.如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE≌△ACD的是(? )
A.?∠B=∠C????????????????????????B.?AD=AE??????????????????????????C.?∠BDC=∠CEB??????????????????????????D.?BE=CD
9.如图,已知 ,以 两点为圆心,大于 的长为半径画圆弧,两弧相交于点 ,连接 与 相交于点 ,则 的周长为(?? )
A.?8??????????????????????????????????????????B.?9??????????????????????????????????????????C.?11??????????????????????????????????????????D.?13
10.已知在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,下列条件中,不一定能得到△ABC≌△A′B′C′的是( )
A.?BC=B'C'????????????????????????B.?∠A=∠A′???????????????????????C.?∠C=∠C′????????????????????????D.?∠B=∠B′=90°
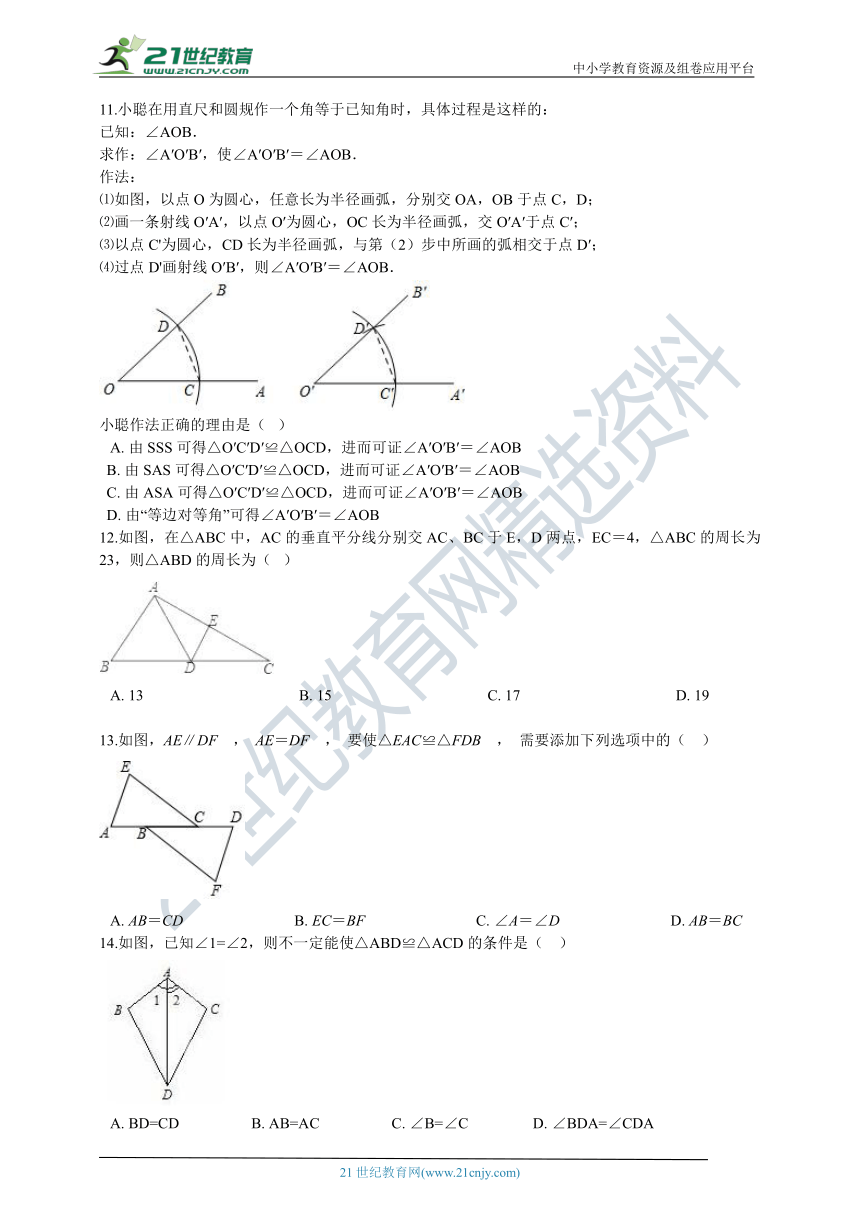
11.小聪在用直尺和圆规作一个角等于已知角时,具体过程是这样的:
已知:∠AOB.
求作:∠A′O′B′,使∠A′O′B′=∠AOB.
作法:
⑴如图,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
⑵画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
⑶以点C'为圆心,CD长为半径画弧,与第(2)步中所画的弧相交于点D′;
⑷过点D'画射线O′B′,则∠A′O′B′=∠AOB.
小聪作法正确的理由是(? )
A.?由SSS可得△O′C′D′≌△OCD,进而可证∠A′O′B′=∠AOB
B.?由SAS可得△O′C′D′≌△OCD,进而可证∠A′O′B′=∠AOB
C.?由ASA可得△O′C′D′≌△OCD,进而可证∠A′O′B′=∠AOB
D.?由“等边对等角”可得∠A′O′B′=∠AOB
12.如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为(? )
A.?13?????????????????????????????????????????B.?15?????????????????????????????????????????C.?17?????????????????????????????????????????D.?19
13.如图,AE∥DF , AE=DF , 要使△EAC≌△FDB , 需要添加下列选项中的(?? )
A.?AB=CD?????????????????????????????B.?EC=BF?????????????????????????????C.?∠A=∠D?????????????????????????????D.?AB=BC
14.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是(?? )
A.?BD=CD???????????????????B.?AB=AC???????????????????C.?∠B=∠C?????????????????D.?∠BDA=∠CDA
15.下列条件中,不能判定两个直角三角形全等的是(? )
A.?一个锐角和斜边对应相等????????????????????????????????????B.?两条直角边对应相等
C.?两个锐角对应相等??????????????????????????????????????????????D.?斜边和一直角边对应相等
二、填空题
16.如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是________.
17.在△ABC中,AD为∠BAC的角平分线.若添加一个条件:________,则△ABD≌△ACD.
18.如图,直线l为线段 的垂直平分线,垂足为C , 直线l上的两点E , F位于 异侧(E , F两点不与点C重合).只需添加一个条件即可证明 ,这个条件可以是________.
19.如图,点A,D,B,E在同一条直线上,AD=BE , AC=EF , 要使△ABC≌△EDF , 只需添加一个条件,这个条件可以是________ .
20.如图,点A,F,C,D在同一条直线上, , ,请你添加一个条件________,使得 .
21.如图, ,只需添加一个条件即可证明 ,这个条件可以是________(写出一个即可)
22.如图,点 , , 在同一条直线上, ,请你只添加一个条件,使得 .你添加的条件是________.(要求:不再添加辅助线,只需填一个答案即可)
23.如图,在 和 中, , ,只需添加一个条件即可证明 ,这个条件可以是________(写出一个即可).
24.如图, 平分 ,点B在射线 上,若使 ,则还需添加的一个条件是________(只填一个即可).
25.如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于________ cm.
三、计算题
26.如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.
27.如图,∠C=∠D=90°,DA=CB,∠CBA=28°,求∠DAC.
28.如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
四、解答题(共1题;共5分)
29.如图,已知 平分 , .求证: .
五、综合题
30.如图,点A,E,F在直线l上, , .
(1)请你只添加一个条件(不再加辅助线),使 ,你添加的条件是________;
(2)添加了条件后,证明 .
答案解析部分
一、单选题
1. B
考点:三角形全等的判定
解:选项A,添加 ,
在 和 中,
?,
∴ ≌ (ASA),
选项B,添加 ,
在 和 中, , , ,无法证明 ≌ ;
选项C,添加 ,
在 和 中,
?,
∴ ≌ (SAS);
选项D,添加 ,
在 和 中,
?,
∴ ≌ (AAS);
综上,只有选项B符合题意.
故答案为:B.
感悟:由图形可知:隐含条件为BC=CB,已知了∠ACB=∠DBC,可以添加另一组对应角相等或添加边AC=DB,再对各选项逐一判断.
2. A
考点:三角形全等的判定
解: ,
,
,
,即 ,
当 时,满足 ,无法判定 ,故A选项符合题意;
当 时,满足 ,可以判定 ,故B选项不合题意;
当 时,满足 ,可以判定 ,故C选项不合题意;
当 时,满足 ,可以判定 ,故D选项不合题意;
故答案为:A.
感悟:根据全等三角形的判定方法逐项判断即可.
3. A
考点:三角形全等的判定
解:由作法得AE=AF , DF=DE ,
而AD为公共边,
所以根据“SSS”可判断△AFD≌△AED .
故答案为:A .
感悟:利用基本作图得到AE=AF , DF=DE , 再根据全等三角形的判定方法进行判断。
4. C
考点:角平分线的性质
解:如图所示,过点D作DE⊥AB于点E ,
由作图知AP平分∠BAC ,
∵∠C=∠AED=90°,
∴CD=DE=3,
∵BD=5,
∴BE=4,
∵AD=AD , CD=DE ,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE ,
设AC=AE=x ,
由AC2+BC2=AB2得x2+82=(x+4)2 ,
解得:x=6,即AC=6,
故答案为:C.
感悟:作DE⊥AB , 由作图知AP平分∠BAC , 依据∠C=∠AED=90°知CD=DE=3,结合BD=5知BE=4,再证Rt△ACD≌Rt△AED得AC=AE , 设AC=AE=x , 由AC2+BC2=AB2得x2+82=(x+4)2 , 解之可得答案.
5. C
考点:三角形全等的判定
解:A.∵∠ABC=∠ABD,∠C=∠D=90°,AB=AB,
∴Rt△ABC≌Rt△ABD(AAS),故本选项不符合题意;
B.∵∠BAC=∠BAD,∠C=∠D=90°,AB=AB,
∴Rt△ABC≌Rt△ABD(AAS),故本选项不符合题意;
C.∵∠C=∠D=90°,AB=AB,AC=AD,
∴Rt△ABC≌Rt△ABD(HL),故本选项符合题意;
D.根据∠C=∠D=90°,AB=AB,AC=BC不能推出Rt△ABC≌Rt△ABD,故本选项不符合题意;
故答案为:C.
感悟:利用“HL”证明三角形全等的方法逐项判定即可。
6. D
考点:三角形全等的判定
解:A、顶角对应相等的两个等腰三角形是AAA,不符合全等的条件,故不能判定两三角形全等,故本选项不符合题意;
B、只有底边相等,别的边,角均不确定,不符合全等的条件,故不能判定两三角形全等,故本选项不符合题意;
C、两腰对应相等,第三边不一定对应相等,不符合全等的条件,故不能判定两三角形全等,故本选项不符合题意;
D、一腰和底边对应相等,相当于两腰和底边对应相等,利用SSS可以证得两个等腰三角形全等,故本选项符合题意.
故答案为:D.
感悟:根据全等三角形的判定定理求解即可。
7. A
考点:三角形全等的判定
解:A.AB=DE,BC=DC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,AB=DE,BC=EC,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
∵∠B=∠E,AB=DE,
∴△ABC≌△DEC(AAS),故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故答案为:A.
感悟:利用三角形全等的判定方法逐项判定即可。
8. D
考点:三角形全等的判定
解:A、根据ASA即可证明三角形全等,本选项不符合题意.
B、根据SAS即可证明三角形全等,本选项不符合题意.
C、根据AAS或ASA即可证明三角形全等,本选项不符合题意.
D、SSA不能判定三角形全等,本选项符合题意.
故答案为:D.
感悟:利用全等三角形的判定方法进行求解即可。
9. A
考点:线段垂直平分线的性质
解:由作法得 垂直平分
(线段垂直平分线的定义),
的周长 ,
故答案为::A.
感悟:利用线段垂直平分线的性质可证得DA=DB,再证明△BDC的周长=AC+BC,然后代入计算.
10. C
考点:三角形全等的判定
解:A、由AB=A′B′,AC=A′C′,BC=B'C'可以判定△ABC≌△A′B′C′(SSS),不符合题意.
B、由AB=A′B′,AC=A′C′,∠A=∠A′可以判定△ABC≌△A′B′C′(SAS),不符合题意.
C、由AB=A′B′,AC=A′C′,∠C=∠C′不可以判定△ABC≌△A′B′C′(SSA),符合题意.
D、由AB=A′B′,AC=A′C′,∠B=∠B′=90°可以判定Rt△ABC≌Rt△A′B′C′(HL),不符合题意.
故答案为:C .
感悟:三角形的判定方法有SSS、SAS、ASA、AAS、HL(直角三角形),据此逐一判断即可.
11. A
考点:三角形全等的判定
解:由作图得OD=OC=OD′=OC′,CD=C′D′,
则根据“SSS”可判断△C′O′D′≌△COD.
故答案为:A.
感悟:根据作图过程可知OD=OC=OD′=OC′,CD=C′D′,然后根据全等三角形的判定方法即可解答.
12. B
考点:线段垂直平分线的性质
∵DE垂直平分AC,
∴AD=CD,AC=2EC=8,
∵C△ABC=AC+BC+AB=23,
∴AB+BC=23-8=15,
∴C△ABD=AB+AD+BD=AB+DC+BD=AB+BC=15.
故答案为:B.
感悟:先求出AD=CD,AC=2EC=8,再求出AB+BC=15,最后求周长即可。
13. A
考点:三角形全等的判定
解:∵AE∥DF,
∴∠A=∠D,
添加AB=CD时,可得AC= DB,
在△AEC和△DFB中,
∴ ,
△AEC≌△DFB(SAS),
而添加EC=BF或∠A=∠D或AB=BC时,不能判定△EAC丰OFDB.
感悟:若已知一边和一角对应相等,则找这个角另一边相等,则添加AB=CD时,可得AC=DB,利用边角边定理判定△AEC≌△DFB.
14. A
考点:三角形全等的判定
解:A、当BD=CD,AD=AD,∠1=∠2时,SSA不能证明 △ABD≌△ACD ,故A符合题意;
B、在△ABD和△ACD中
∴△ABD≌△ACD(SAS)故B不符合题意;
C、在△ABD和△ACD中
∴△ABD≌△ACD(AAS)故C不符合题意;
D、在△ABD和△ACD中
∴△ABD≌△ACD(ASA)故D不符合题意;
故答案为:A.
感悟:图形中的隐含条件是:AD=AD;利用SSA不能证明两三角形全等,可对A作出判断,利用SAS,AAS,ASA可证明两三角形全等,可对B,C,D作出判断.
15. C
考点:三角形全等的判定
解:A、一个锐角和斜边对应相等,符合AAS的全等判定条件,故此选项不符合题意;
B、两条直角边对应相等,符合SAS的全等判定条件,故此选项不符合题意;
C、两个锐角对应相等,全等三角形的判定必须有边的参与,故此选项符合题意;
D、斜边和一条直角边对应相等,符合HL的全等判定条件,故此选项不符合题意.
故答案为:C.
感悟:利用全等三角形的判断方法,对各选项逐一判断.
二、填空题
16. 12
考点:线段垂直平分线的性质
解:∵直线DE垂直平分BC,
∴ ,
∴△ABD的周长 ,
故答案为:12.
感悟:利用线段垂直平分线的性质可证得DB=DC,由此可证得△ABD的周长就是AB+AC的值.
17.
考点:三角形全等的判定
当AD⊥BC时,∠ADB=∠ADC=90°,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD,
故答案为:AD⊥BC.
感悟:先求出∠BAD=∠CAD,再利用SAS证明△ABD≌△ACD即可。
18. CE=CF
考点:三角形全等的判定
证明:添加: ,理由如下:
∵直线l为线段 的垂直平分线
∴AC=CB,∠ACE=∠BCF
又
∴ (SAS)
故答案为:CE=CF
感悟:符合全等三角形的判定定理即可。
19. ∠A=∠E
考点:三角形全等的判定
解:增加一个条件:∠A=∠E ,
∵AD=BE ,
∴AB=DE ,
在△ABC和△FDE中, ,
∴△ABC≌△EDF(SAS).
故答案为:∠A=∠E(答案不唯一).
感悟:利用三角形的判定方法求解即可。
20. 或 或 (答案不唯一)
考点:三角形全等的判定
解: ,
,
若添加 ,且 ,由“ ”可证 ;
若添加 ,且 ,由“ ”可证 ;
若添加 ,且 ,由“ ”可证 ;
故答案为: 或 或 (答案不唯一).
感悟:由全等三角形的判定定理可求解.
21. AD=BC或∠D=∠C或∠DBA=∠CAB等(答案不唯一,填一个即可)
考点:三角形全等的判定
解:添加AD=BC , 可用SAS判断 ;
添加∠D=∠C , 可用AAS判断 ;
添加∠DBA=∠CAB , 可用ASA判断 ;
故答案为:AD=BC或∠D=∠C或∠DBA=∠CAB等(答案不唯一,填一个即可).
感悟:根据三角形全等的判定定理,添加边相等或角相等即可.
22. DA=BC
考点:三角形全等的判定
解:添加条件为:DA=BC
∵∠DBE=∠A=∠C=90°,
∴∠D+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠D=∠CBE,
在△DAB和△BCE中
∴△DAB≌△BCE(AAS)
故答案为:DA=BC.
感悟:利用余角的性质可证得∠D=∠CBE,有两组对应角相等,由此只需添加三组对应边中的任意一组对应边相等,都可得到△DAB≌△BCE.
23. (答案不唯一)
考点:三角形全等的判定
解:在 与 中,
= ,AC=AC,
若 ,
则由AAS可得 .
故答案为: (答案不唯一).
感悟:利用全等三角形的判定方法求解即可。
24. AC=AD或 或
考点:三角形全等的判定
解:因为AE平分∠CAD,
所以∠CAB=∠DAB,
又∵AB=AB,
已具备一边一角,
从边上考虑,只能添加AC=AD,
在△ABC和△ABD中,
,
,
从角上考虑,可添加 或 ,
添加
在△ABC和△ABD中,
,
,
添加 ,
在△ABC和△ABD中,
,
,
故答案为:AC=AD或 或 .
感悟:利用全等三角形的判定方法求解即可。
25. 10
考点:线段垂直平分线的性质
解:∵AB的垂直平分线交AB于点D
∴AE=BE
∴AE+CE=BE+CE
∵△BCE的周长等于18cm,BC=8cm
∴BE+CE+BC=18,
∴AE+CE+BC=18,
∴AC+BC=18,
∴AC+8=18,
∴AC=10cm
故答案为:10.
感悟:根据垂直平分线的性质可得AE=BE,再利用三角形的周长计算出AC的长即可。
三、计算题
26. 解:结论:DF=AE.理由:∵AB∥CD,∴∠C=∠B,∵CE=BF,∴CF=BE,∵CD=AB,∴△CDF≌△BAE,∴DF=AE.
考点:全等三角形的判定与性质
感悟:由AB∥CD,可证得∠C=∠B,再由CE=BF,可得出CF=BE,然后利用SAS证明△CDF≌△BAE,根据全等三角形的性质可证得结论。
27. 解:在Rt△ABC和Rt△BAD中, ,
∴Rt△ABC≌Rt△BAD(HL),
∴∠DAB=∠CBA=28°,
∵∠C=90°,
∴∠BAC=90°﹣∠CBA=90°﹣28°=62°,
∴∠DAC=∠BAC﹣∠DAB=62°﹣28°=34°
考点:全等三角形的判定与性质
感悟:利用“HL”证明Rt△ABC和Rt△BAD全等,根据全等三角形对应角相等可得∠DAB=∠CBA,根据直角三角形两锐角互余求出∠BAC,再根据∠DAC=∠BAC﹣∠DAB代入数据计算即可得解.
28. 解:如图,连接BE,
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,
又∵AC=BC,DC=EC,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∵AC=BC=6,
∴AB=6 ,
∵∠BAC=∠CAE=45°,
∴∠BAE=90°,
在Rt△BAE中,AB=6 ,AE=3,
∴BE= = = =9,
∴AD=9.
考点:全等三角形的判定与性质
感悟:连接BE,根据已知条件先证出∠BCE=∠ACD,根据SAS证出△ACD≌△BCE,得出AD=BE,再根据勾股定理求出AB,然后根据∠BAC=∠CAE=45°,求出∠BAE=90°,在Rt△BAE中,根据AB、AE的值,求出BE,从而得出AD.
四、解答题
29. 证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD与△CBD中,
,
∴△ABD≌△CBD(AAS).
考点:角平分线的性质
感悟:根据角平分线的性质,结合题意,证明三角形全等即可。
五、综合题
30. (1)∠CAF=∠DBE
(2)证明:∵AE=BF,
? ∴AF=BE,
在△ACF和△BDE中,
,
∴△ACF≌△BDE(SAS) .
考点:三角形全等的判定
感悟:(1)由AE=BF得出AF=BE,添加∠CAF=∠DBE,根据SAS可证?;
(2)由AE=BF得出AF=BE,添加∠CAF=∠DBE,根据SAS可证?.
_21?????????è?????(www.21cnjy.com)_
初中数学浙教版八年级上册1.5 三角形全等的判定 同步练习
一、单选题
1.如图,在 和 中, ,添加一个条件,不能证明 和 全等的是(?? )
A.????????????????????B.????????????????????C.????????????????????D.?
2.如图,B、E、C、F在同一直线上,BE=CF,AB∥DE,请你添加一个合适的条件,使△ABC≌△DEF,其中不符合三角形全等的条件是(?? )
A.?AC=DF???????????????????????????B.?AB=DE???????????????????????????C.?∠A=∠D???????????????????????????D.?∠ACB=∠F
3.如图,用尺规作图作∠BAC的平分线AD , 第一步是以A为圆心,任意长为半径画弧,分别交AB , AC于点E , F;第二步是分别以E , F为圆心,以大于 EF长为半径画弧,两圆弧交于D点,连接AD , AD即为所求作,请说明△AFD≌△AED的依据是(??? )
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?AAS
4.如图,在 中, ,按以下步骤作图:①以点 为圆心,以小于 的长为半径作弧,分别交 , 于点 , ;②分别以点 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;③连接 ,交 于点 .若 , ,则 的长为(?? )
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
5.如图,已知∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是(? )
A.?∠ABC=∠ABD??????????????????B.?∠BAC=∠BAD??????????????????????C.?AC=AD??????????????????????D.?AC=BC
6.下列判定两个等腰三角形全等的方法中,正确的是(? )
A.?顶角对应相等????????????B.?底边对应相等????????????????C.?两腰对应相等????????????D.?一腰和底边对应相等
7.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,添加的一组条件错误的是(? )
A.?BC=DC,∠A=∠D????????????????????????????????????????????B.?BC=EC,AC=DC
C.?∠B=∠E,∠BCE=∠ACD????????????????????????????????????D.?BC=EC,∠B=∠E
8.如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE≌△ACD的是(? )
A.?∠B=∠C????????????????????????B.?AD=AE??????????????????????????C.?∠BDC=∠CEB??????????????????????????D.?BE=CD
9.如图,已知 ,以 两点为圆心,大于 的长为半径画圆弧,两弧相交于点 ,连接 与 相交于点 ,则 的周长为(?? )
A.?8??????????????????????????????????????????B.?9??????????????????????????????????????????C.?11??????????????????????????????????????????D.?13
10.已知在△ABC和△A′B′C′中,AB=A′B′,AC=A′C′,下列条件中,不一定能得到△ABC≌△A′B′C′的是( )
A.?BC=B'C'????????????????????????B.?∠A=∠A′???????????????????????C.?∠C=∠C′????????????????????????D.?∠B=∠B′=90°
11.小聪在用直尺和圆规作一个角等于已知角时,具体过程是这样的:
已知:∠AOB.
求作:∠A′O′B′,使∠A′O′B′=∠AOB.
作法:
⑴如图,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
⑵画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;
⑶以点C'为圆心,CD长为半径画弧,与第(2)步中所画的弧相交于点D′;
⑷过点D'画射线O′B′,则∠A′O′B′=∠AOB.
小聪作法正确的理由是(? )
A.?由SSS可得△O′C′D′≌△OCD,进而可证∠A′O′B′=∠AOB
B.?由SAS可得△O′C′D′≌△OCD,进而可证∠A′O′B′=∠AOB
C.?由ASA可得△O′C′D′≌△OCD,进而可证∠A′O′B′=∠AOB
D.?由“等边对等角”可得∠A′O′B′=∠AOB
12.如图,在△ABC中,AC的垂直平分线分别交AC、BC于E,D两点,EC=4,△ABC的周长为23,则△ABD的周长为(? )
A.?13?????????????????????????????????????????B.?15?????????????????????????????????????????C.?17?????????????????????????????????????????D.?19
13.如图,AE∥DF , AE=DF , 要使△EAC≌△FDB , 需要添加下列选项中的(?? )
A.?AB=CD?????????????????????????????B.?EC=BF?????????????????????????????C.?∠A=∠D?????????????????????????????D.?AB=BC
14.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是(?? )
A.?BD=CD???????????????????B.?AB=AC???????????????????C.?∠B=∠C?????????????????D.?∠BDA=∠CDA
15.下列条件中,不能判定两个直角三角形全等的是(? )
A.?一个锐角和斜边对应相等????????????????????????????????????B.?两条直角边对应相等
C.?两个锐角对应相等??????????????????????????????????????????????D.?斜边和一直角边对应相等
二、填空题
16.如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是________.
17.在△ABC中,AD为∠BAC的角平分线.若添加一个条件:________,则△ABD≌△ACD.
18.如图,直线l为线段 的垂直平分线,垂足为C , 直线l上的两点E , F位于 异侧(E , F两点不与点C重合).只需添加一个条件即可证明 ,这个条件可以是________.
19.如图,点A,D,B,E在同一条直线上,AD=BE , AC=EF , 要使△ABC≌△EDF , 只需添加一个条件,这个条件可以是________ .
20.如图,点A,F,C,D在同一条直线上, , ,请你添加一个条件________,使得 .
21.如图, ,只需添加一个条件即可证明 ,这个条件可以是________(写出一个即可)
22.如图,点 , , 在同一条直线上, ,请你只添加一个条件,使得 .你添加的条件是________.(要求:不再添加辅助线,只需填一个答案即可)
23.如图,在 和 中, , ,只需添加一个条件即可证明 ,这个条件可以是________(写出一个即可).
24.如图, 平分 ,点B在射线 上,若使 ,则还需添加的一个条件是________(只填一个即可).
25.如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于________ cm.
三、计算题
26.如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.
27.如图,∠C=∠D=90°,DA=CB,∠CBA=28°,求∠DAC.
28.如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
四、解答题(共1题;共5分)
29.如图,已知 平分 , .求证: .
五、综合题
30.如图,点A,E,F在直线l上, , .
(1)请你只添加一个条件(不再加辅助线),使 ,你添加的条件是________;
(2)添加了条件后,证明 .
答案解析部分
一、单选题
1. B
考点:三角形全等的判定
解:选项A,添加 ,
在 和 中,
?,
∴ ≌ (ASA),
选项B,添加 ,
在 和 中, , , ,无法证明 ≌ ;
选项C,添加 ,
在 和 中,
?,
∴ ≌ (SAS);
选项D,添加 ,
在 和 中,
?,
∴ ≌ (AAS);
综上,只有选项B符合题意.
故答案为:B.
感悟:由图形可知:隐含条件为BC=CB,已知了∠ACB=∠DBC,可以添加另一组对应角相等或添加边AC=DB,再对各选项逐一判断.
2. A
考点:三角形全等的判定
解: ,
,
,
,即 ,
当 时,满足 ,无法判定 ,故A选项符合题意;
当 时,满足 ,可以判定 ,故B选项不合题意;
当 时,满足 ,可以判定 ,故C选项不合题意;
当 时,满足 ,可以判定 ,故D选项不合题意;
故答案为:A.
感悟:根据全等三角形的判定方法逐项判断即可.
3. A
考点:三角形全等的判定
解:由作法得AE=AF , DF=DE ,
而AD为公共边,
所以根据“SSS”可判断△AFD≌△AED .
故答案为:A .
感悟:利用基本作图得到AE=AF , DF=DE , 再根据全等三角形的判定方法进行判断。
4. C
考点:角平分线的性质
解:如图所示,过点D作DE⊥AB于点E ,
由作图知AP平分∠BAC ,
∵∠C=∠AED=90°,
∴CD=DE=3,
∵BD=5,
∴BE=4,
∵AD=AD , CD=DE ,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE ,
设AC=AE=x ,
由AC2+BC2=AB2得x2+82=(x+4)2 ,
解得:x=6,即AC=6,
故答案为:C.
感悟:作DE⊥AB , 由作图知AP平分∠BAC , 依据∠C=∠AED=90°知CD=DE=3,结合BD=5知BE=4,再证Rt△ACD≌Rt△AED得AC=AE , 设AC=AE=x , 由AC2+BC2=AB2得x2+82=(x+4)2 , 解之可得答案.
5. C
考点:三角形全等的判定
解:A.∵∠ABC=∠ABD,∠C=∠D=90°,AB=AB,
∴Rt△ABC≌Rt△ABD(AAS),故本选项不符合题意;
B.∵∠BAC=∠BAD,∠C=∠D=90°,AB=AB,
∴Rt△ABC≌Rt△ABD(AAS),故本选项不符合题意;
C.∵∠C=∠D=90°,AB=AB,AC=AD,
∴Rt△ABC≌Rt△ABD(HL),故本选项符合题意;
D.根据∠C=∠D=90°,AB=AB,AC=BC不能推出Rt△ABC≌Rt△ABD,故本选项不符合题意;
故答案为:C.
感悟:利用“HL”证明三角形全等的方法逐项判定即可。
6. D
考点:三角形全等的判定
解:A、顶角对应相等的两个等腰三角形是AAA,不符合全等的条件,故不能判定两三角形全等,故本选项不符合题意;
B、只有底边相等,别的边,角均不确定,不符合全等的条件,故不能判定两三角形全等,故本选项不符合题意;
C、两腰对应相等,第三边不一定对应相等,不符合全等的条件,故不能判定两三角形全等,故本选项不符合题意;
D、一腰和底边对应相等,相当于两腰和底边对应相等,利用SSS可以证得两个等腰三角形全等,故本选项符合题意.
故答案为:D.
感悟:根据全等三角形的判定定理求解即可。
7. A
考点:三角形全等的判定
解:A.AB=DE,BC=DC,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项符合题意;
B.AC=DC,AB=DE,BC=EC,符合全等三角形的判定定理SSS,能推出△ABC≌△DEC,故本选项不符合题意;
C.∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠ACB=∠DCE,
∵∠B=∠E,AB=DE,
∴△ABC≌△DEC(AAS),故本选项不符合题意;
D.AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项不符合题意;
故答案为:A.
感悟:利用三角形全等的判定方法逐项判定即可。
8. D
考点:三角形全等的判定
解:A、根据ASA即可证明三角形全等,本选项不符合题意.
B、根据SAS即可证明三角形全等,本选项不符合题意.
C、根据AAS或ASA即可证明三角形全等,本选项不符合题意.
D、SSA不能判定三角形全等,本选项符合题意.
故答案为:D.
感悟:利用全等三角形的判定方法进行求解即可。
9. A
考点:线段垂直平分线的性质
解:由作法得 垂直平分
(线段垂直平分线的定义),
的周长 ,
故答案为::A.
感悟:利用线段垂直平分线的性质可证得DA=DB,再证明△BDC的周长=AC+BC,然后代入计算.
10. C
考点:三角形全等的判定
解:A、由AB=A′B′,AC=A′C′,BC=B'C'可以判定△ABC≌△A′B′C′(SSS),不符合题意.
B、由AB=A′B′,AC=A′C′,∠A=∠A′可以判定△ABC≌△A′B′C′(SAS),不符合题意.
C、由AB=A′B′,AC=A′C′,∠C=∠C′不可以判定△ABC≌△A′B′C′(SSA),符合题意.
D、由AB=A′B′,AC=A′C′,∠B=∠B′=90°可以判定Rt△ABC≌Rt△A′B′C′(HL),不符合题意.
故答案为:C .
感悟:三角形的判定方法有SSS、SAS、ASA、AAS、HL(直角三角形),据此逐一判断即可.
11. A
考点:三角形全等的判定
解:由作图得OD=OC=OD′=OC′,CD=C′D′,
则根据“SSS”可判断△C′O′D′≌△COD.
故答案为:A.
感悟:根据作图过程可知OD=OC=OD′=OC′,CD=C′D′,然后根据全等三角形的判定方法即可解答.
12. B
考点:线段垂直平分线的性质
∵DE垂直平分AC,
∴AD=CD,AC=2EC=8,
∵C△ABC=AC+BC+AB=23,
∴AB+BC=23-8=15,
∴C△ABD=AB+AD+BD=AB+DC+BD=AB+BC=15.
故答案为:B.
感悟:先求出AD=CD,AC=2EC=8,再求出AB+BC=15,最后求周长即可。
13. A
考点:三角形全等的判定
解:∵AE∥DF,
∴∠A=∠D,
添加AB=CD时,可得AC= DB,
在△AEC和△DFB中,
∴ ,
△AEC≌△DFB(SAS),
而添加EC=BF或∠A=∠D或AB=BC时,不能判定△EAC丰OFDB.
感悟:若已知一边和一角对应相等,则找这个角另一边相等,则添加AB=CD时,可得AC=DB,利用边角边定理判定△AEC≌△DFB.
14. A
考点:三角形全等的判定
解:A、当BD=CD,AD=AD,∠1=∠2时,SSA不能证明 △ABD≌△ACD ,故A符合题意;
B、在△ABD和△ACD中
∴△ABD≌△ACD(SAS)故B不符合题意;
C、在△ABD和△ACD中
∴△ABD≌△ACD(AAS)故C不符合题意;
D、在△ABD和△ACD中
∴△ABD≌△ACD(ASA)故D不符合题意;
故答案为:A.
感悟:图形中的隐含条件是:AD=AD;利用SSA不能证明两三角形全等,可对A作出判断,利用SAS,AAS,ASA可证明两三角形全等,可对B,C,D作出判断.
15. C
考点:三角形全等的判定
解:A、一个锐角和斜边对应相等,符合AAS的全等判定条件,故此选项不符合题意;
B、两条直角边对应相等,符合SAS的全等判定条件,故此选项不符合题意;
C、两个锐角对应相等,全等三角形的判定必须有边的参与,故此选项符合题意;
D、斜边和一条直角边对应相等,符合HL的全等判定条件,故此选项不符合题意.
故答案为:C.
感悟:利用全等三角形的判断方法,对各选项逐一判断.
二、填空题
16. 12
考点:线段垂直平分线的性质
解:∵直线DE垂直平分BC,
∴ ,
∴△ABD的周长 ,
故答案为:12.
感悟:利用线段垂直平分线的性质可证得DB=DC,由此可证得△ABD的周长就是AB+AC的值.
17.
考点:三角形全等的判定
当AD⊥BC时,∠ADB=∠ADC=90°,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD,
故答案为:AD⊥BC.
感悟:先求出∠BAD=∠CAD,再利用SAS证明△ABD≌△ACD即可。
18. CE=CF
考点:三角形全等的判定
证明:添加: ,理由如下:
∵直线l为线段 的垂直平分线
∴AC=CB,∠ACE=∠BCF
又
∴ (SAS)
故答案为:CE=CF
感悟:符合全等三角形的判定定理即可。
19. ∠A=∠E
考点:三角形全等的判定
解:增加一个条件:∠A=∠E ,
∵AD=BE ,
∴AB=DE ,
在△ABC和△FDE中, ,
∴△ABC≌△EDF(SAS).
故答案为:∠A=∠E(答案不唯一).
感悟:利用三角形的判定方法求解即可。
20. 或 或 (答案不唯一)
考点:三角形全等的判定
解: ,
,
若添加 ,且 ,由“ ”可证 ;
若添加 ,且 ,由“ ”可证 ;
若添加 ,且 ,由“ ”可证 ;
故答案为: 或 或 (答案不唯一).
感悟:由全等三角形的判定定理可求解.
21. AD=BC或∠D=∠C或∠DBA=∠CAB等(答案不唯一,填一个即可)
考点:三角形全等的判定
解:添加AD=BC , 可用SAS判断 ;
添加∠D=∠C , 可用AAS判断 ;
添加∠DBA=∠CAB , 可用ASA判断 ;
故答案为:AD=BC或∠D=∠C或∠DBA=∠CAB等(答案不唯一,填一个即可).
感悟:根据三角形全等的判定定理,添加边相等或角相等即可.
22. DA=BC
考点:三角形全等的判定
解:添加条件为:DA=BC
∵∠DBE=∠A=∠C=90°,
∴∠D+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠D=∠CBE,
在△DAB和△BCE中
∴△DAB≌△BCE(AAS)
故答案为:DA=BC.
感悟:利用余角的性质可证得∠D=∠CBE,有两组对应角相等,由此只需添加三组对应边中的任意一组对应边相等,都可得到△DAB≌△BCE.
23. (答案不唯一)
考点:三角形全等的判定
解:在 与 中,
= ,AC=AC,
若 ,
则由AAS可得 .
故答案为: (答案不唯一).
感悟:利用全等三角形的判定方法求解即可。
24. AC=AD或 或
考点:三角形全等的判定
解:因为AE平分∠CAD,
所以∠CAB=∠DAB,
又∵AB=AB,
已具备一边一角,
从边上考虑,只能添加AC=AD,
在△ABC和△ABD中,
,
,
从角上考虑,可添加 或 ,
添加
在△ABC和△ABD中,
,
,
添加 ,
在△ABC和△ABD中,
,
,
故答案为:AC=AD或 或 .
感悟:利用全等三角形的判定方法求解即可。
25. 10
考点:线段垂直平分线的性质
解:∵AB的垂直平分线交AB于点D
∴AE=BE
∴AE+CE=BE+CE
∵△BCE的周长等于18cm,BC=8cm
∴BE+CE+BC=18,
∴AE+CE+BC=18,
∴AC+BC=18,
∴AC+8=18,
∴AC=10cm
故答案为:10.
感悟:根据垂直平分线的性质可得AE=BE,再利用三角形的周长计算出AC的长即可。
三、计算题
26. 解:结论:DF=AE.理由:∵AB∥CD,∴∠C=∠B,∵CE=BF,∴CF=BE,∵CD=AB,∴△CDF≌△BAE,∴DF=AE.
考点:全等三角形的判定与性质
感悟:由AB∥CD,可证得∠C=∠B,再由CE=BF,可得出CF=BE,然后利用SAS证明△CDF≌△BAE,根据全等三角形的性质可证得结论。
27. 解:在Rt△ABC和Rt△BAD中, ,
∴Rt△ABC≌Rt△BAD(HL),
∴∠DAB=∠CBA=28°,
∵∠C=90°,
∴∠BAC=90°﹣∠CBA=90°﹣28°=62°,
∴∠DAC=∠BAC﹣∠DAB=62°﹣28°=34°
考点:全等三角形的判定与性质
感悟:利用“HL”证明Rt△ABC和Rt△BAD全等,根据全等三角形对应角相等可得∠DAB=∠CBA,根据直角三角形两锐角互余求出∠BAC,再根据∠DAC=∠BAC﹣∠DAB代入数据计算即可得解.
28. 解:如图,连接BE,
∵∠ACB=∠DCE=90°,
∴∠ACB+∠ACE=∠DCE+∠ACE,
即∠BCE=∠ACD,
又∵AC=BC,DC=EC,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∵AC=BC=6,
∴AB=6 ,
∵∠BAC=∠CAE=45°,
∴∠BAE=90°,
在Rt△BAE中,AB=6 ,AE=3,
∴BE= = = =9,
∴AD=9.
考点:全等三角形的判定与性质
感悟:连接BE,根据已知条件先证出∠BCE=∠ACD,根据SAS证出△ACD≌△BCE,得出AD=BE,再根据勾股定理求出AB,然后根据∠BAC=∠CAE=45°,求出∠BAE=90°,在Rt△BAE中,根据AB、AE的值,求出BE,从而得出AD.
四、解答题
29. 证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD与△CBD中,
,
∴△ABD≌△CBD(AAS).
考点:角平分线的性质
感悟:根据角平分线的性质,结合题意,证明三角形全等即可。
五、综合题
30. (1)∠CAF=∠DBE
(2)证明:∵AE=BF,
? ∴AF=BE,
在△ACF和△BDE中,
,
∴△ACF≌△BDE(SAS) .
考点:三角形全等的判定
感悟:(1)由AE=BF得出AF=BE,添加∠CAF=∠DBE,根据SAS可证?;
(2)由AE=BF得出AF=BE,添加∠CAF=∠DBE,根据SAS可证?.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
