6.1 矩形

(共28张PPT)
矩 形
观察平行四边形的框架,回答下列问题:
(1) 为什么这个框架会任意”摇摆”
(2) 随着内角的变化情况,平行四边形的面积有没有发生变化 内角为何值时图形面积最大？这时是什么图形？
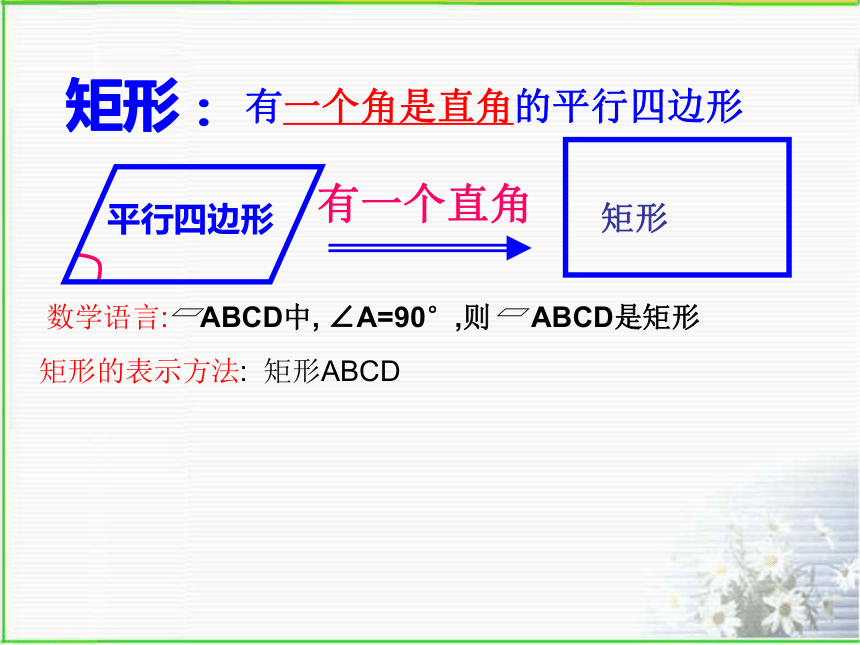
矩形：
有一个角是直角的平行四边形
矩形：
有一个直角
平行四边形
数学语言: ABCD中, ∠A=90°,则 ABCD是矩形
矩形的表示方法: 矩形ABCD
矩形
中心对称图形
对称性
对角线互相平分
对角线
对角相等，邻角互补
角
对边平行且相等
边
矩形的性质
平行四边形的性质
元素
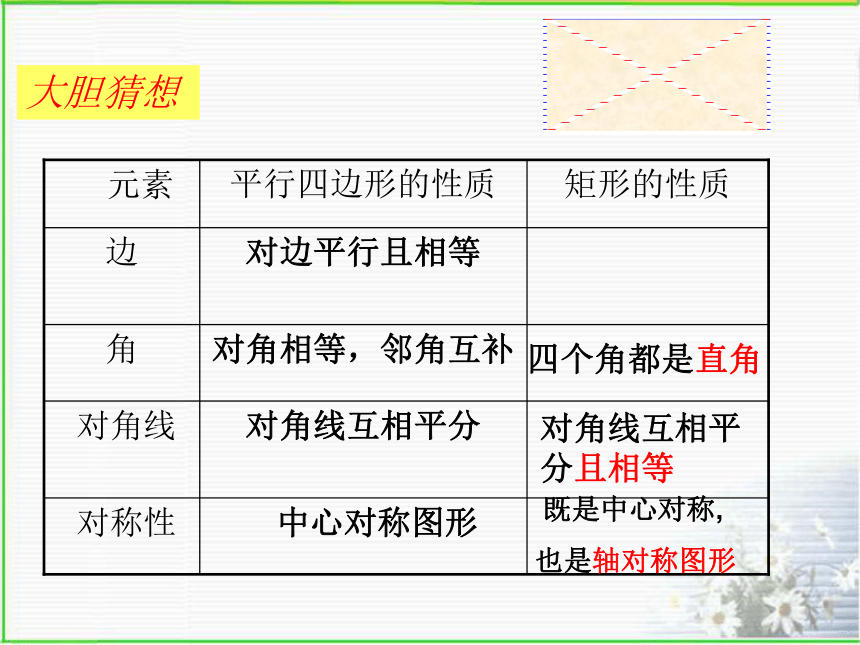
大胆猜想
四个角都是直角
对角线互相平
分且相等
既是中心对称,
也是轴对称图形
矩形的性质
A
B
C
D
已知：四边形ABCD是矩形，∠A＝900
求证：∠A= ∠B = ∠C=∠D=900
矩形的四个角都是直角
猜想1
矩形的性质定理1
A
B
C
D
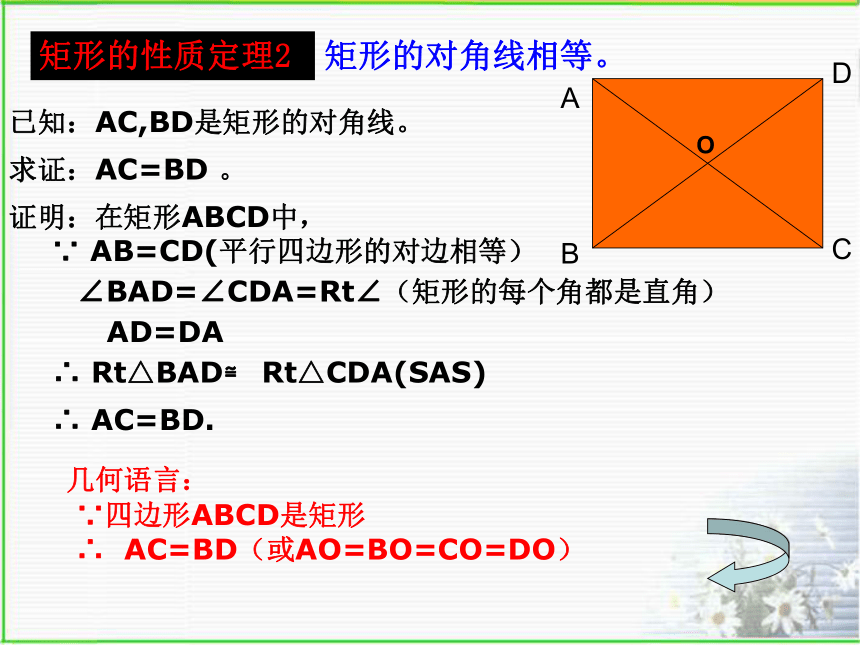
已知：AC,BD是矩形的对角线。
求证：AC=BD 。
证明：在矩形ABCD中，
∵ AB=CD(平行四边形的对边相等）
∠BAD=∠CDA=Rt∠（矩形的每个角都是直角）
AD=DA
∴ Rt△BAD≌ Rt△CDA(SAS)
∴ AC=BD.
猜想2： 矩形的对角线相等。
几何语言：
∵四边形ABCD是矩形
∴ AC=BD（或AO=BO=CO=DO）
O
矩形的性质定理2
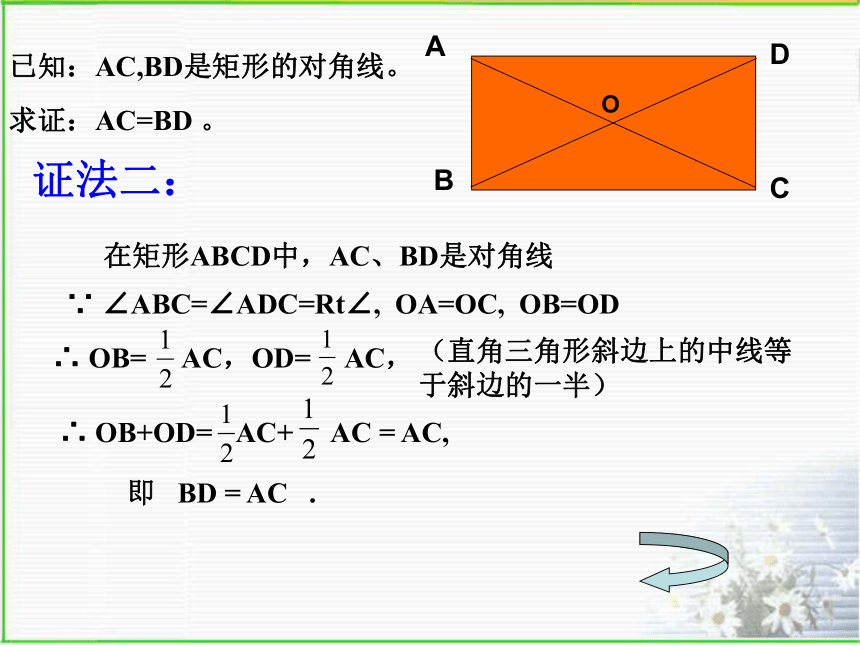
证法二：
A
B
C
D
O
已知：AC,BD是矩形的对角线。
求证：AC=BD 。
在矩形ABCD中，AC、BD是对角线
即 BD = AC .
∴ OB+OD=
AC+
AC = AC,
∴ OB=
AC，OD=
AC，
（直角三角形斜边上的中线等于斜边的一半）
∵ ∠ABC=∠ADC=Rt∠, OA=OC, OB=OD
A
B
C
D
O
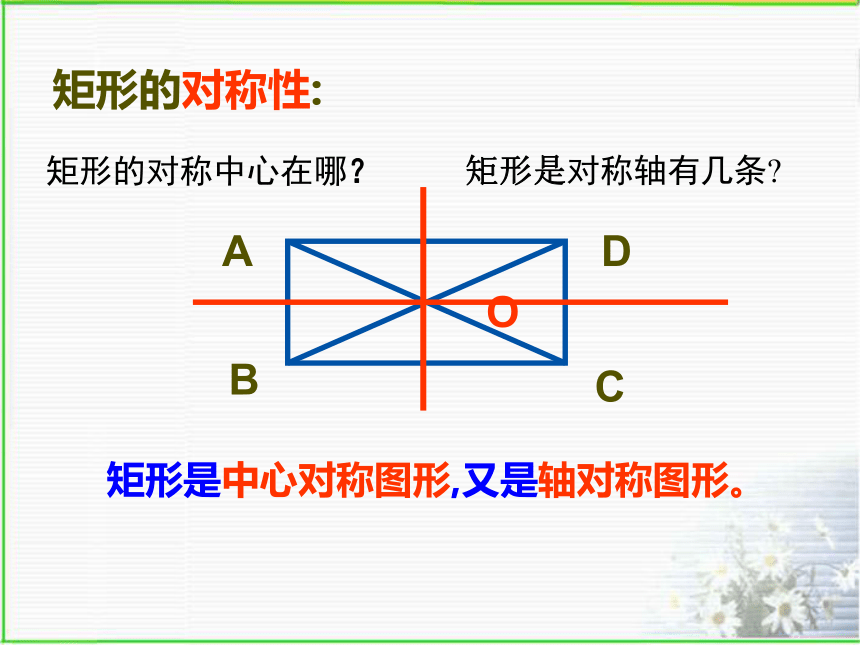
矩形的对称性:
矩形是中心对称图形,又是轴对称图形。
矩形的对称中心在哪？
矩形是对称轴有几条
已知: 在矩形ABCD中,E、F分别是AB、CD的中点.
求证：四边形AEFD是矩形.
（2）
分析: 矩形的定义是什么
先证 四边形AEFD是平行四边形,
再证 其有一个角是直角就可以得证
巩固新知
问题1
（1）由OA=OB=OC=OD可知图中有几
个等腰三角形？有几对全等三角形
O
A
B
C
D
E
巩固新知
（3）若∠AOD=120度，AB=4厘米，求矩形的对
角线长.
问题2：如图，矩形ABCD的两条对
角线相交于点O
O
A
B
C
D
（1）若∠AOD=120度，试判断
ΔAOB的形状。
（2）若要得到ΔAOB是等边三角形，你可以添加一
个什么条件？
巩固新知
1.在矩形ABCD中,AE⊥BD于E，若BE=OE=1，则
AC=_____,AB＝______∠AOB=_____________.
O
（1）
2
4
60度
E
D
B
A
C
运用性质，提高能力
变式：已知:如图,在矩形ABCD中, 对角线相交于点O,
∠AOB=60°,AE平分∠BAD,AE交BC于E,求∠BOE的度数.
O
D
C
B
A
E
75°
运用性质，提高能力
A
B
C
D
E
F
2、 矩形ABCD，折叠矩形的一边AD，使D点落在BC边上的点F处，已知AB=8，BC=10，求：EC的长
运用性质，提高能力
变式：已知如图，矩形OABC的长为 ，宽OC
为1，将⊿AOC沿AC翻折得⊿ APC．
求：（1）∠PCB的度数
（2）点P的坐标
挑战中考
E
F
翻折
全等
相等的边，相等的角
收获：
通过本节课的学习，
你有哪些收获拿出来
和大家分享吧！
QQ日志：他乡遇“故知”
今天，我与老朋友——矩形重逢.又得知了他的一些信息:
矩形是一个________________.所以他具有_________
的所有性质。
矩形区别于平行四边形的性质有三个：
①___________;②_________; ③______________
我还学会了用它来解题，在解题过程中，我发现：
矩形问题要分割成___________________来解决.
还应用到了直角三角形的两个“一半”：
①____________________________;
②____________________________;
……
特殊的平行四边形
平行四边形
四个角都是直角
对角线相等
它是一个轴对称图形
等腰三角形和直角三角形
直角三角形斜边上的中线等于斜边的一半
30°所对的直角边等于斜边的一半
收获 小结
1.一个定义：
2.二个定理:
3.二个结论:
(1)矩形的两条对角线被交点分成的四条线段相等
(2)矩形既是轴对称图形，又是中心对称图形
这节课你学到了什么 还有什么困惑吗？
送给大家的祝福:
忧愁是可减的！
快乐是可加的！
在未来趋于正无穷大的日子里，
幸福是连续的！
对你的祝福是正数的绝对值，
它一定是大于零的！
祝你每天的快乐和幸福是连续
上升的折线统计图
作业：
1、如图，在矩形ABCD中，M为BC的中点
求证：AM=DM
M
A
B
C
D
2、你还有其他的方法证明矩形对角线相等吗？
已知:如图,过矩形ABCD的顶点作CE//BD， 交AB的延长线于E。 求证：∠CAE=∠CEA
A
B
C
D
E
相信你,一定行
练习：
1、已知矩形的周长是14cm,相邻两边的差
是1cm, 那么这个矩形的面积是多少？
2、如图，在矩形ABCD中，对角线AC，BD相交
于点O，已知AB=2cm,AC=6cm,则BC= ？cm,
ΔBOC 的周长=？ cm.
O
A
B
C
D
收获
创设情境，引出课题
观察思考:
(1)当平行四边形的一个锐角变为钝角的过程中,得到的平行四边形有什么变与不变的量.
自主学习，发现新知：
A
B
C
D
E
A
B
C
D
（E）
(2)在这些平行四边形中,有没有面积最大的一个平行四边形 说出你的理由;
(3)这个面积最大的平行四边形的内角有什么特点 观察变化过程
中面积最大的平行四边形的特征,请给它下一个定义.
(1) 矩形是不是平行四边形
(2) 平行四边形是不是矩形
(3) 平行四边形的性质矩形具备吗
(4) 矩形是否有与平行四边形不同的性质
实质上：矩形是特殊的平行四边形。
合作学习，再探新知
既然矩形是特殊的平行四边形，那么它和平行四边形相比特殊在哪里？哪些性质改变了，哪些未性质改变？
对角相等，邻角互补
对边平行且相等
对角线互相平分
元素 平行四边形的性质
中心对称
角
边
对角线
对称性
四个角都是角
邻边互相垂直
对角线互相平
分且相等
元素 平行四边形的性质 矩形的性质
角 对角相等，邻角互补
边 对边平行且相等
对角线 对角线互相平分
对称性 中心对称图形
既是中心对称,
也是轴对称图形
大胆猜想
矩 形