7.5 一次函数的简单应用

(共21张PPT)
一次函数的应用
热身练习
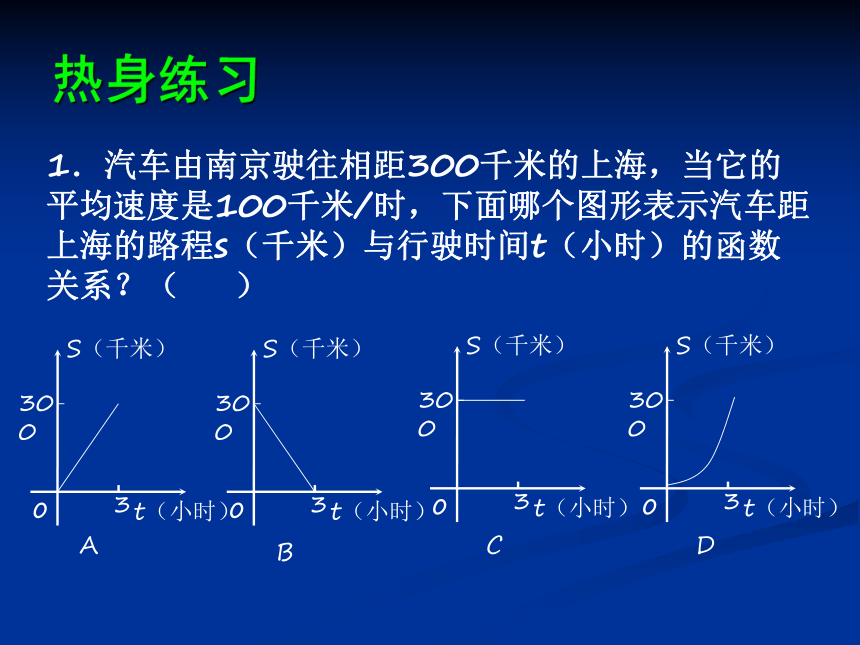
1．汽车由南京驶往相距300千米的上海，当它的平均速度是100千米/时，下面哪个图形表示汽车距上海的路程s（千米）与行驶时间t（小时）的函数关系？（ ）
S（千米）
t（小时）
o
300
3
S（千米）
t（小时）
o
300
3
S（千米）
t（小时）
o
300
3
S（千米）
t（小时）
o
300
3
A
B
C
D
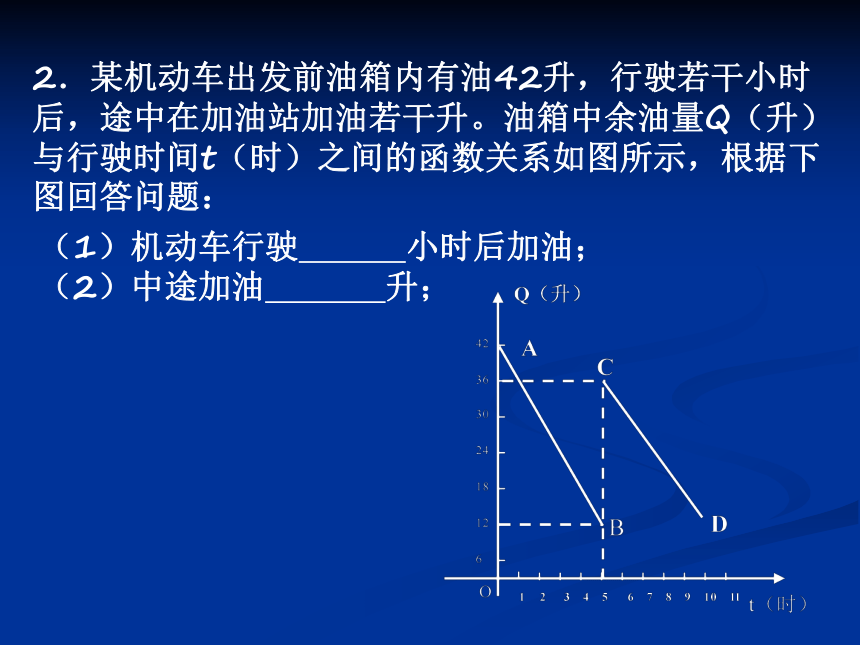
2．某机动车出发前油箱内有油42升，行驶若干小时后，途中在加油站加油若干升。油箱中余油量Q（升）与行驶时间t（时）之间的函数关系如图所示，根据下图回答问题：
（1）机动车行驶 小时后加油；
（2）中途加油 升；
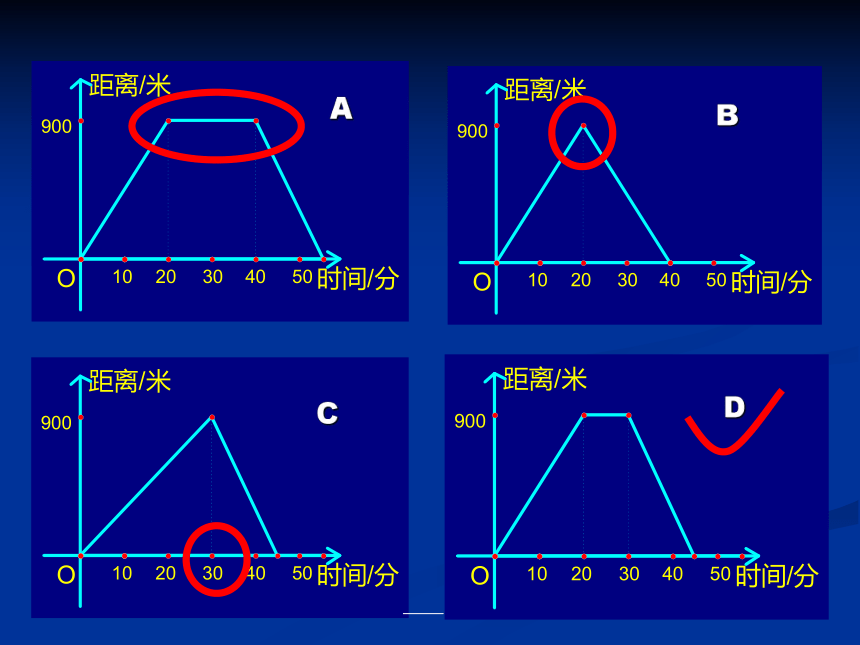
3、小明出去散步，从家走了20分钟， 到了一个离家900米的阅报亭，看了10分钟报纸后，用了15分钟返回到家。下面能够表示小明离家时间与离家距离之间的关系的是（ ）
从家走了20分钟，
到了一个离家900米的阅报亭，
看了10分钟报纸后，
用了15分钟返回到家。
A
D
C
B
D
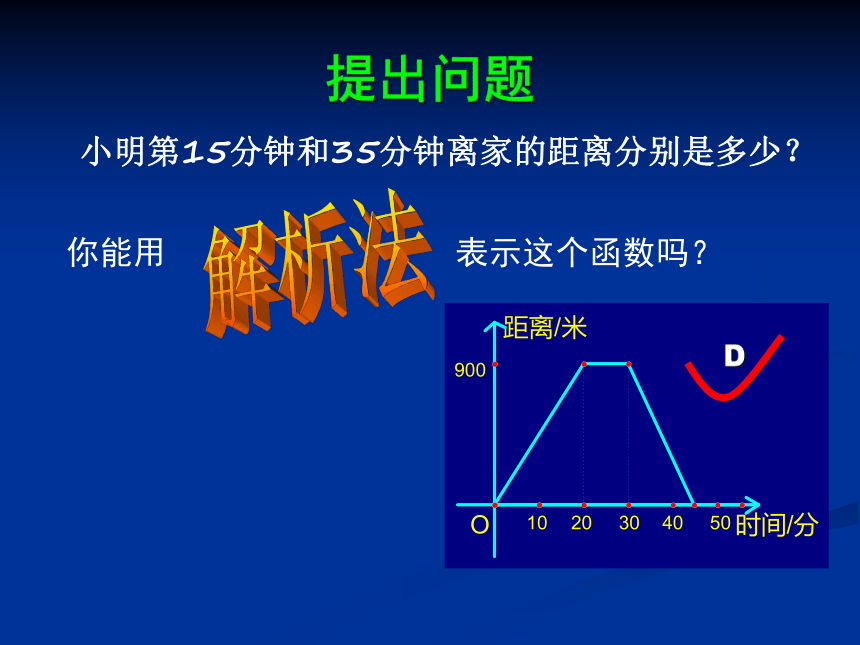
你能用 表示这个函数吗？
小明第15分钟和35分钟离家的距离分别是多少？
提出问题
变式训练
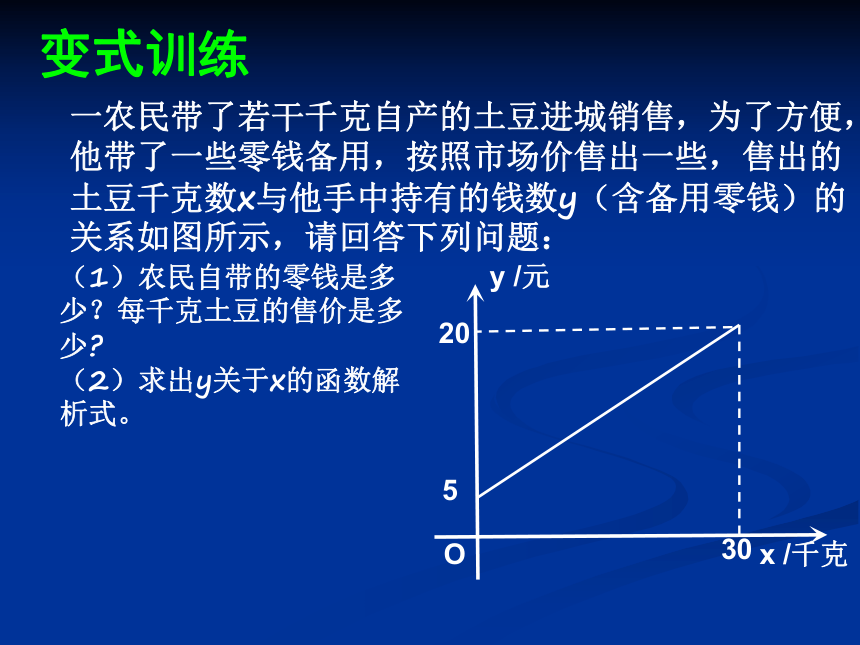
一农民带了若干千克自产的土豆进城销售，为了方便，他带了一些零钱备用，按照市场价售出一些，售出的土豆千克数x与他手中持有的钱数y（含备用零钱）的关系如图所示，请回答下列问题：
5
20
30
O
x /千克
y /元
（1）农民自带的零钱是多少？每千克土豆的售价是多少
（2）求出y关于x的函数解析式。
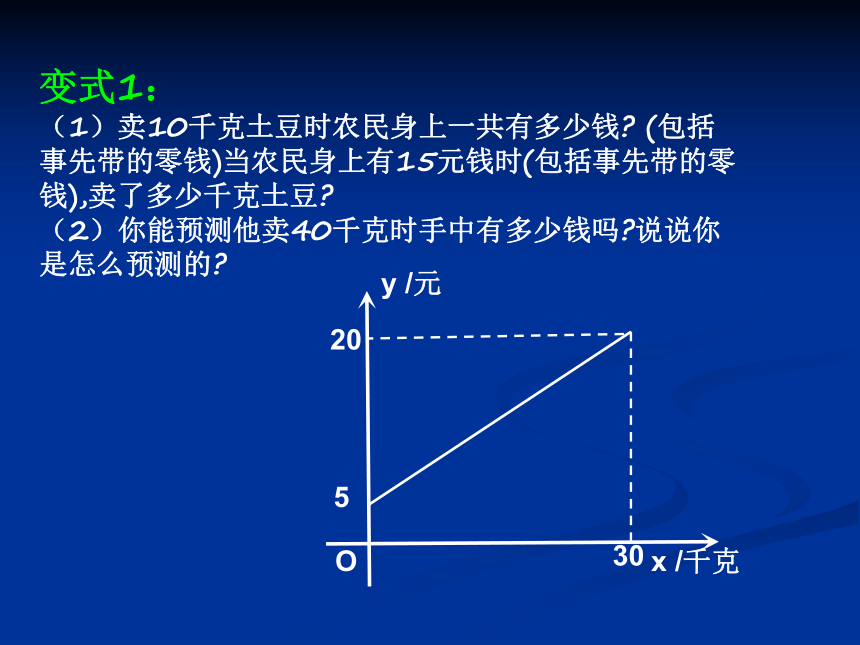
变式1：
（1）卖10千克土豆时农民身上一共有多少钱 (包括事先带的零钱)当农民身上有15元钱时(包括事先带的零钱),卖了多少千克土豆
（2）你能预测他卖40千克时手中有多少钱吗 说说你是怎么预测的
5
20
30
O
x /千克
y /元
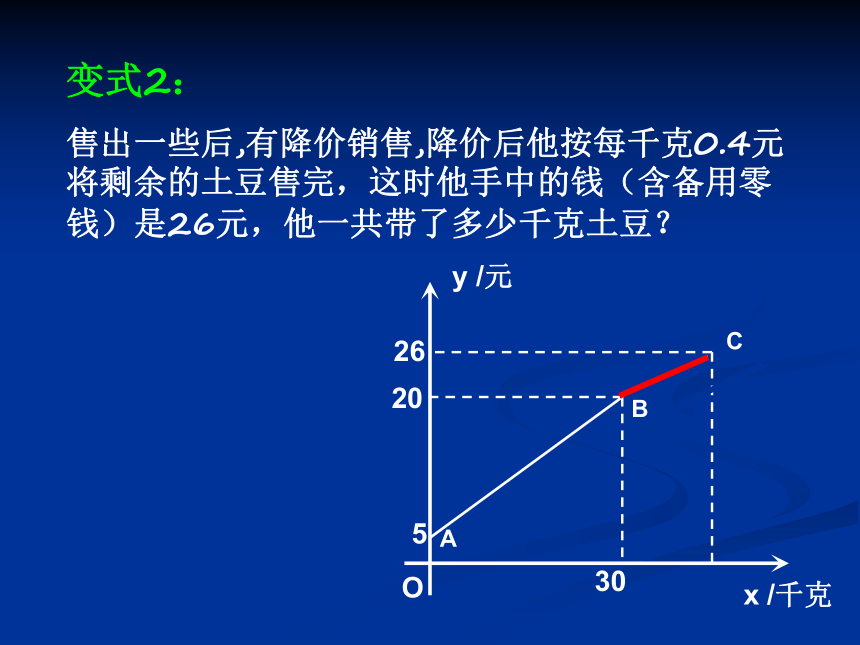
变式2：
售出一些后,有降价销售,降价后他按每千克0.4元将剩余的土豆售完，这时他手中的钱（含备用零钱）是26元，他一共带了多少千克土豆？
5
20
26
30
O
x /千克
y /元
A
B
C
分段函数
(1) 这个整体是一个函数。
(2) 函数y 在 x的某个范围内可能是特殊函数,如一次函数。
(3) 由于问题的不同，分段函数也可能在自变量某范围内不是一次函数而是其他形式的函数，在这里我们不予讨论。
议一议
我们周围的还存在哪些分段函数的实例。
如：出租车计费问题，
阶梯水费、电费，
个人所得税，
邮资等等
D
你能用 表示这个函数吗？
小明第15分钟和35分钟离家的距离分别是多少？
解决问题
测试
1. (如图)某产品的生产流水线每小时可以生产100件产品，生产前没有产品积压，生产3小时后，安排1人装箱,若每小时装产品150件，未装箱的产品数量（Y）是生产时间X的函数，那么，这个函数的大致图像只能是（ ）。
( A ) ( B ) ( C ) ( D )
2、为了缓解用电紧张矛盾，某电力公司特制定了新的用电收费标准，每月用电量x（度）与应付电费y（元）的关系如图所示。
（1）根据图象，请分别求出当0≤x≤50和x＞50时，y与x的函数解析式；
（2）请回答：当每月用电量不超过50度时， 收费标准是 __________；当每月用电量超过50度时，收费标准是_____________.
O
25
50
75
100
25
50
75
70
y（元）
x（度）
3、某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用后，那么服药后2小时血液中含药量最高，达每毫升6微克，（1微克=10-3毫克），接着逐步衰减，10小时时血液中含药量为每毫升3微克，每毫升血液中含药量y（微克）随时间x（小时）的变化如图所示。当成人按规定剂量服用后：
（1）分别求0≤x≤2和x≥2时，y与x之间的函数解析式；
（2）如果每毫升血液中含药量为4微克以 上时，在治疗疾病时是有效的，那么这个有效的时间是多长？
x/时
y/毫克
6
3
2
10
O
1
2
O
－1
－2
－1
1
2
x
y
（1）当y=0时，x＝
（2）直线对应的函数表达式是
（3）方程0.5x+1=0的解是
－2
y=0.5x+1
X=－2
1
2
O
－1
－2
－1
1
2
x
y
（4）方程0.5x+1=0与一次函数y=0.5x+1有什么联系？
结论：方程kx+b=0的解是一次函数y=kx+b的图象与x轴交点的横坐标。
师生共同小结
一个模型：分段函数
一个方法：数学模型方法
一种数学思想：分类讨论
一种意识：
数学“源于生活、寓于生活、用于生活”
课后作业
基础巩固：目标练习册P28.2，P30.2
能力提高：分小组选题，结合身边的生活实例调查、编写、分析一个分段函数的实例。