2.6 直角三角形 同步练习（含解析）

中小学教育资源及组卷应用平台
初中数学浙教版八年级上册2.6 直角三角形 同步练习
一、单选题
1.已知直角三角形中30°角所对的直角边为2cm，则斜边的长为（ ）
A.?2cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?6cm?????????????????????????????????????D.?8cm
2.如图，在 中， ， ， ，则 的度数为（?? ）
A.?12°???????????????????????????????????????B.?13°???????????????????????????????????????C.?14°???????????????????????????????????????D.?15°
3.一副三角板如图方式摆放，点D在直线EF上，且AB//EF，则∠ADE的度数是（?? ）
A.?105°??????????????????????????????????????B.?75°??????????????????????????????????????C.?60°??????????????????????????????????????D.?45°
4.如图所示，在正五边形 中，过顶点A作 ，垂足为点F，连接对角线 ，则 的度数是（?? ）
A.?16°???????????????????????????????????????B.?18°???????????????????????????????????????C.?24°???????????????????????????????????????D.?28°
5.如图，在Rt ABC中，∠C＝90°，∠A＝30°，AB+BC＝9cm，则AB的长为（　　）
A.?3cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?5cm?????????????????????????????????????D.?6cm
6.学校研究性学习小组的同学测量旗杆的高度．如图，在教学楼一楼地面C处测得旗杆顶部的仰角为 ，在教学楼三楼地面D处测得旗杆顶部的仰角为 ，旗杆底部与教学楼一楼在同一水平线上，已知教学楼每层楼的高度约为3.3米，则旗杆 的高度最接近（??? ）
A.?8米?????????????????????????????????????B.?9米?????????????????????????????????????C.?10米?????????????????????????????????????D.?11米
7.如图，在 中， ， ，DE垂直平分AB ， 交BC于点E ， ，则 （??? ）
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
8.如图，Rt△ABC中，∠C＝90°，∠B＝30°，∠BAC的平分线AD交BC于点D ， CD ，则BD的长是（?? ）
A.?2????????????????????????????????????????B.?2 ????????????????????????????????????????C.?3????????????????????????????????????????D.?3
9.如图，在 中，点O是边 和 的垂直平分线 、 的交点，若 ，则这两条垂直平分线相交所成锐角 的度数为（ ??）
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
10.如图： ．按下列步骤作图：①在射线 上取一点C ， 以点O为圆心， 长为半径作圆弧 ，交射线 于点F ． 连结 ；②以点F为圆心， 长为半径作圆弧，交弧 于点G；③连结 、 ．作射线 ．根据以上作图过程及所作图形，下列结论中错误的是（??? ）
A.??????????????????B.? 垂直平分 ?????????????????C.??????????????????D.?
11.如图，在等边△ABC中，点D和点B关于直线AC对称，连接CD，过D作DE⊥BC，交BC的延长线于点E，若CE＝5，则BE的长为（?? ）
A.?10?????????????????????????????????????B.?15?????????????????????????????????????C.??????????????????????????????????????D.?
12.如图， ，将一个含 角的直角三角尺按如图所示的方式放置，若 的度数为 ，则 的度数为（ ）
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
13.如图，Rt△ABC中， 于点D则下列结论不一定成立的是（?? ）
A.?????????????????????B.?????????????????????C.?????????????????????D.?
14.如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，则它们的公共部分的面积等于（? ）
A.?1﹣ ???????????????????????????????????B.?1﹣ ???????????????????????????????????C.????????????????????????????????????D.?
15.如图，在△ABC中，∠C＝60°，AD是BC边上的高，点E为AD的中点，连接BE并延长交AC于点F．若∠AFB＝90°，EF＝2，则BF长为（? ）
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
二、填空题
16.如图，在 中，点E在 上，且 平分 ，若 ， ，则 的面积为________.
17.如图，点D是∠ABC内一点，点B在射线BA上，且∠DBE=∠BDE=15°，DE∥BC，过点D作DF⊥BC，垂足为点F，若BE=10，则DF=________．
18.如图，已知直线a∥b，c⊥d，∠1=36°，则∠2的度数是________.
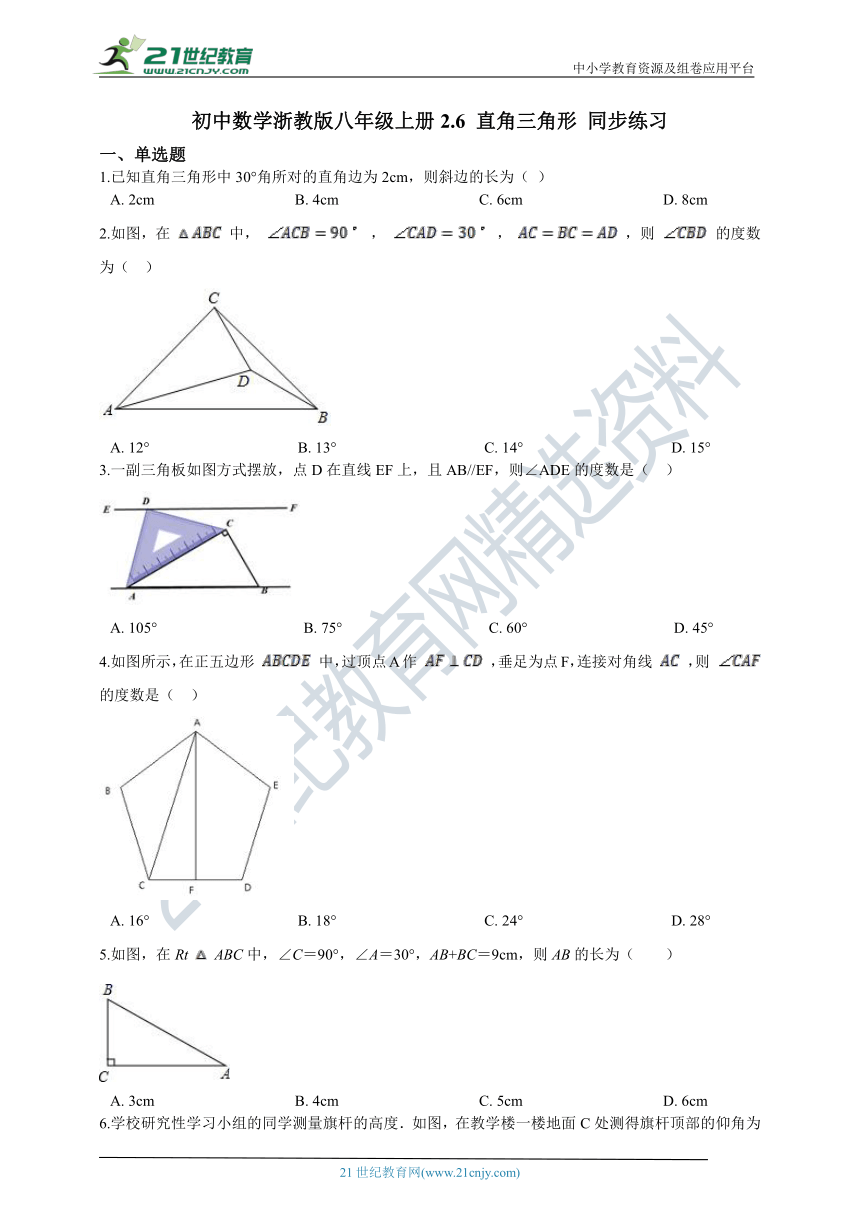
19.如图，在Rt△ABC中，∠C=90°，∠BAC=40°，将Rt△ABC绕点A旋转得到Rt△AB'C'，且点C'落在AB上，则∠B'BC的度数为________

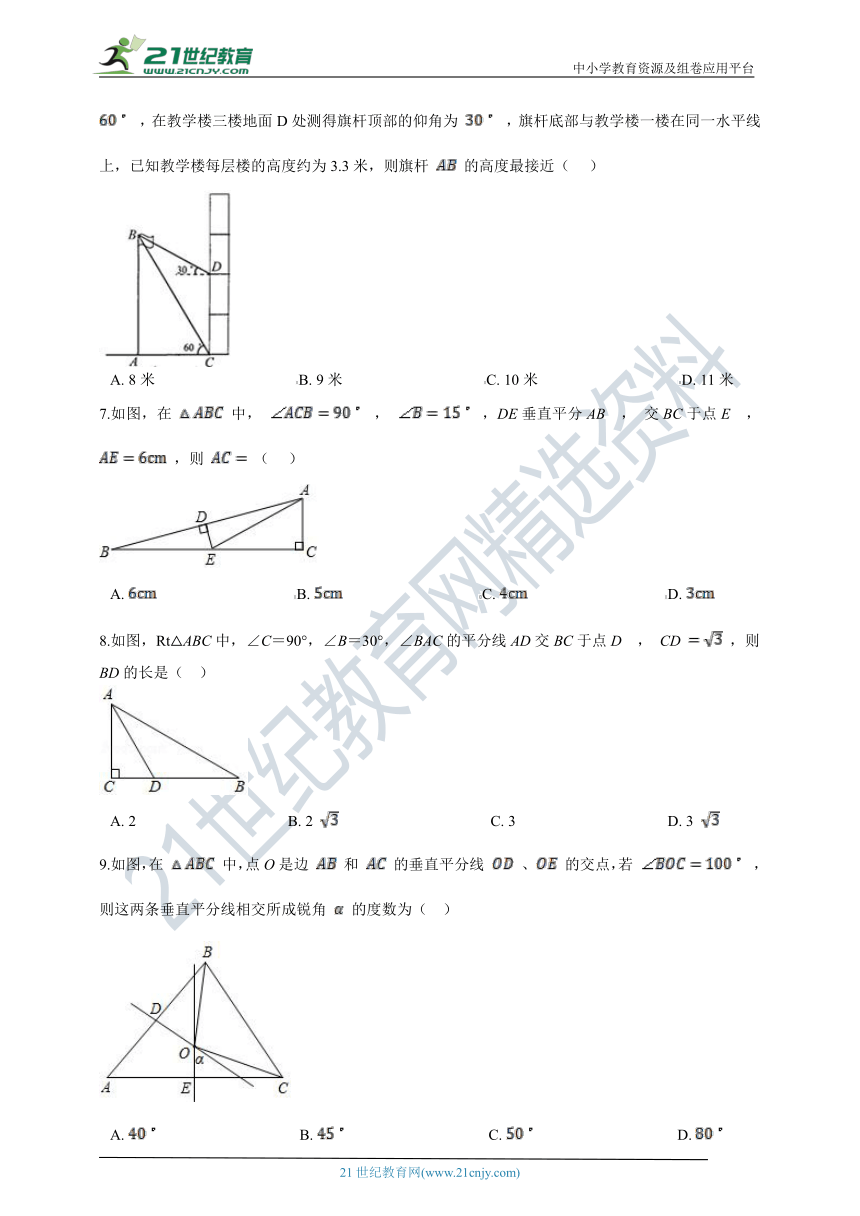
20.如图，AB是一座办公大楼，一架无人机从C处测得楼顶部B的仰角为60°，测得楼底部A的俯角为37°，测得与大楼的水平距离为40米，则该办公大楼的高度是________米．（结果保留整数，参考数据： ≈1.73，sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）
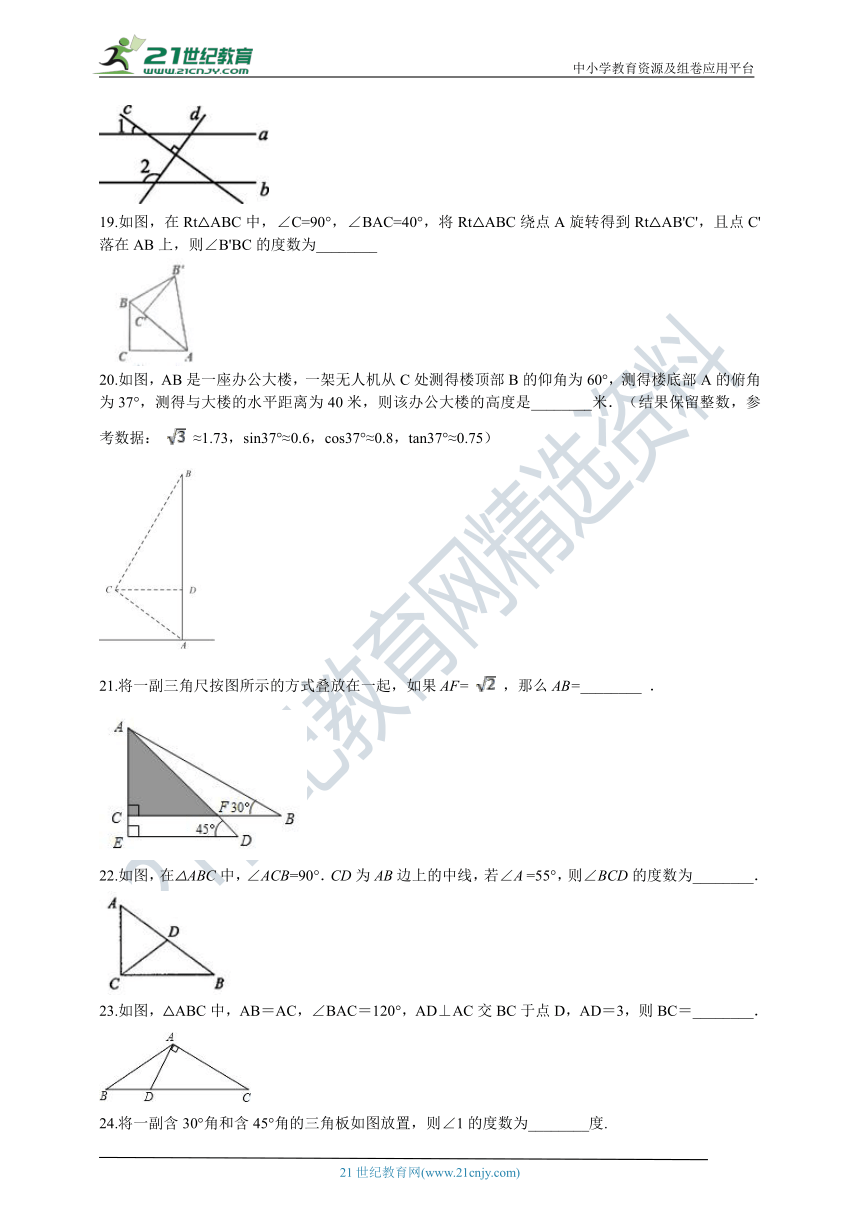
21.将一副三角尺按图所示的方式叠放在一起，如果AF= ，那么AB=________ ．
22.如图，在△ABC中，∠ACB=90°．CD为AB边上的中线，若∠A =55°，则∠BCD的度数为________．
23.如图，△ABC中，AB＝AC，∠BAC＝120°，AD⊥AC交BC于点D，AD＝3，则BC＝________．
24.将一副含30°角和含45°角的三角板如图放置，则∠1的度数为________度.
25.如图等边三角形ABC中，点O是△ABC的∠B和∠C的角平分线的交点，∠FOG=120°，绕点O旋转∠FOG，分别交线段AB、BC于点D、E两点，连接DE，若OA=2，则△ODE周长最小值为________.
三、计算题
26.如图，在△ABC中，AB=AC，AD⊥BC于点D.
（1）若∠C=42°，求∠BAD的度数；

（2）若点E在边AB上，EF∥AC交AD的延长线于点F. 求证：AE=FE.
四、解答题
27.如图，已知∠AGH=∠B, ∠CGH=∠BEF，EF⊥AB于F，试说明CG⊥AB.
28.在等边△ABC中，点D ， E分别在边BC ， AC上，若CD＝2，过点D作DE∥AB ， 过点E作EF⊥DE ， 交BC的延长线于点F ， 求EF的长．
29.如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AC＝3，AD是△ABC的角平分线，DE⊥AB于点E，连接CE.求CE的长；
五、综合题
30.等腰Rt△ABC，点D为斜边AB上的中点，点E在线段BD上，连结CD，CE，作AH⊥CE，垂足为H，交CD于点G，AH的延长线交BC于点F.
（1）求证：△ADG≌△CDE.
（2）若点H恰好为CE的中点，求证：∠CGF=∠CFG.
31.己知，△ABC是边长为3cm的等边三角形，动点P以1cm/s的速度从点A出发，沿线段AB向点B运动．请分别解决下面四种情况：

（1）如图1，设点P的运动时间为t(s)，那么t=________s时，△PBC是直角三角形；
（2）如图2，若另一动点Q从点B出发，沿线段BC向点C运动，如果动点P、Q都以1cm／s的速度同时出发，设运动时间为t(s)，那么t为何值时，△PBQ是直角三角形?
（3）如图3，若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D，如果动点P、Q都以1cm／s的速度同时出发，设运动时间为t(s)，那么t为何值时，△DCQ是等腰三角形?
（4）如图4，若另一动点Q从点C出发，沿射线BC方向运动，连接PQ交AC于D，连接PC，如果动点P、Q都以1cm/s的速度同时出发．请你猜想：在点P、Q的运动过程中，△PCD和△QCD的面积有什么关系?并说明理由．
答案解析部分
一、单选题
1. B
考点:含30°角的直角三角形
根据直角三角形30°角所对的直角边等于斜边的一半解答．
解∵直角三角形中30°角所对的直角边为2cm，
∴斜边的长为2×2=4cm．
故选B．
本题主要考查了直角三角形30°角所对的直角边等于斜边的一半的性质，是基础题，熟记性质是解题的关键．
2. D
考点:等腰三角形的性质，含30°角的直角三角形，三角形全等的判定（AAS）
解：如图，过C作CE⊥AD于E，过D作DF⊥BC于F.
∵∠CAD=30°，
∴∠ACE=60°，且CE= AC，
∵AC=AD，∠CAD=30°，
∴∠ACD=75°，
∴∠FCD=90°-∠ACD=15°，∠ECD=∠ACD-∠ACE=15°，
在△CED和△CFD中，
，
∴△CED≌△CFD（AAS），
∴CF=CE= AC= BC，
∴CF=BF，
∵DF⊥BC，
∴BD=CD，
∴∠DCB=∠CBD=15°，
故答案为：D.
可过C作CE⊥AD于E，过D作DE⊥BC于F，依据题意可得∠FCD=∠ECD，进而得到△CED≌△CFD，得到CF=BF，再利用等腰三角形的判定可得出结论.
3. B
考点:平行线的性质，直角三角形的性质
解：∠ADE=∠DAC+∠CAB=45°+30°=75°.
故答案为：B.
根据三角板自带角的度数以及平行的性质可得.
4. B
考点:等腰三角形的性质，正多边形的性质，直角三角形的性质
解： 五边形 是正五边形，
， ，
，
，
，
，
故答案为：B.
先根据正五边形的内角和公式可得 和 的度数，再根据等腰三角形的性质可得 的度数，从而可得 的度数，然后根据直角三角形的两锐角互余即可得.
5. D
考点:含30°角的直角三角形
解：在Rt ABC中， ， ，
设 ，由 ，得到 ，
则 ，即 ，
解得： ．
则 ．
故答案为： ．
先求出 ，再求出 ， 最后计算求解即可。
6. C
考点:矩形的性质，直角三角形的性质
解：过点D作DE⊥AB于E ， 如图所示：
则四边形ACDE为矩形，
∴AE＝CD＝2×3.3＝6.6（米），AC＝DE ，
设BE＝x米，
在Rt△BDE中，∠BED＝90°，∠BDE＝30°，
∴DE＝ BE＝ x（米），
∴AC＝DE＝ x（米），
在Rt△ABC中，
∵∠BAC＝90°，∠ACB＝60°，
∴AB＝ AC＝ × x＝3x（米），
∵AB﹣BE＝AE ，
∴3x﹣x＝6.6，
∴x＝3.3，
AB＝3×3.3＝9.9（米），
即旗杆AB的高度为9.9米，
∴旗杆AB的高度最接近10米，
故答案为：C．
根据矩形以及直角三角形的性质，计算得到答案即可。
7. D
考点:三角形的外角性质，线段垂直平分线的性质，含30°角的直角三角形
解： 垂直平分 ，
，
，
，
(cm) ，
故答案为：D．
根据垂直平分线的性质得出EB=EA，由等边对等角可得 ， 利用三角形外角的性质可得∠AEC=30°，根据含30°角的直角三角形的性质可得.
8. B
考点:等腰三角形的判定与性质，含30°角的直角三角形，角平分线的定义
解：
在Rt△ABC中，∠C＝90°，∠B＝30°，
∴∠BAC=60°
∵AD为∠BAC的角平分线
∴∠BAD=∠CAD=∠B=30°
∴AD=BD
在△ACD中，∠CAD=30°，CD=
∴AD=2CD=
∴BD=AD=
故答案为：B

本题考查角平分线的定义、含30°角的直角三角形的性质、等腰三角形的判定以及三角形内角和的计算，先利用三角形内角和与角平分线的定义确定∠B=∠BAD=30°，得到等腰三角形ABD，AD=BD ,再在△ACD中利用30°角所对的直角边是斜边的一半，计算出AD的长，从而得到BD的长。
9. C
考点:三角形内角和定理，线段垂直平分线的性质，等腰三角形的性质，直角三角形的性质
解：连结AO ， DO交AC于F ，
∵边 和 的垂直平分线 、 ，
∴AO=BO=OC ，
∴∠OBA=∠OAB ， ∠OAC=∠OCA ，
∴∠BAC=∠OBA+∠OAC =∠OAB+∠OCA ，
∵ ，
∴∠OBC+∠OCB=180°- ，
∴∠BAC+∠ABO+∠ACO=180°-（∠OBC+∠OCB）=180°-80°=100°，
∴∠BAC+∠ABO+∠ACO=∠BAC +∠BAC =2∠BAC =100°，
∴∠BAC=50° ，
∵OE⊥AC ， OD⊥AB ，
∴∠DAF+∠DFA=90°，∠EOF+∠OFE=90°，∠DFA=∠OFE ，
∴∠EOF=∠DAF=∠BAC=50°，
∴这两条垂直平分线相交所成锐角 =∠BAC=50°．
故答案为：C ．
连结AO，DO交AC于F，根据垂直平分线的性质及等腰三角形的性质，可求出∠BAC=∠OBA+∠OAC =∠OAB+∠OCA，由 ， 利用三角形的内角和可求出∠BAC=50°，由OE⊥AC，OD⊥AB，利用余角的性质可求出∠EOF=∠DAF=∠BAC=50°,从而得出结论.
10. D
考点:线段垂直平分线的性质，等边三角形的判定与性质，含30°角的直角三角形，轴对称的性质，线段垂直平分线的判定
解：由作法得OC=OF= OG ， FG= FC ， 则OF垂直平分CG ，
所以B选项的结论不符合题意；
∵C点与G点关于OF对称
∴∠FOG=∠FOC=30°，
∴∠AOG =60°，
所以A选项的结论不符合题意;
∴△OCG为等边三角形，
OG = CG ，
所以C选项的结论不符合题意;
在Rt△OCM中，∵∠COM =30°
∴OC = 2CM ，
∵CF > CM ， FC= FG ，
∴ OC ≠2FG ，
所以D选项的结论符合题意
故答案为：D.
由尺规作图可得OC=OF= OG，FG= FC，根据线段垂直平分线的判定可得OF垂直平分CG，据此判断B；由C点与G点关于OF对称，可得∠FOG=∠FOC=30°，据此判断A；可得△OCG是等边三角形，可得OG=CG，据此判断C；在Rt△OCM中，∠COM =30°，可得OC = 2CM，在Rt△CMF中，CF＞CM，据此判断D即可.
11. B
考点:等边三角形的性质，轴对称的性质，直角三角形的性质
∵ 点D和点B关于直线AC对称 ，△ABC是等边三角形，
∴BC=CD，∠ACB=∠ACD=60°，
∴∠DCE=60°，
∵DE⊥BC，CE=5，
∴∠CDE=90°-∠DCE=30°，
∴CD=2CE=10，
∴BC=10，
∴BE=BC+CE=10+5=15.
故答案为：B.
根据等边三角形及轴对称的性质得出BC=CD，∠ACB=∠ACD=60°，从而得出∠DCE=60°，根据垂直的定义及直角三角形的定义可求出∠CDE=30°，从而得出CD=2CE=10，即得BC=10，利用BE=BC+CE计算即得结论.
12. A
考点:平行线的判定与性质，含30°角的直角三角形
如图，过三角板60°角的顶点作直线EF∥AB，
∵AB∥CD，
∴EF∥CD，
∴∠3=∠1，∠4=∠2，
∵∠3+∠4=60°，
∴∠1+∠2=60°，
∵∠1=25°，
∴∠2=35°，
故答案为：A．

作直线EF∥AB，由AB∥CD，得EF∥CD，∠3=∠1，∠4=∠2，由∠3+∠4=60°，得∠1+∠2=60°，由此得出∠2的度数。
13. D
考点:三角形内角和定理，直角三角形的性质
解：∵ ，
∴∠3+∠4=90°，∠ADC=∠BDC=90°，
∴∠2+∠4=90°，
A.∵∠3+∠4=90°，∴∠1+∠2=90°，故A成立，不选A；
B.∵∠3+∠4=90°，∠2+∠4=90°，∴∠2=∠3， 故B成立，不选B；
C.∵∠2+∠4=90°，∠1+∠2=90°，∴ ，故C成立，不选C；
D.∵∠3+∠4=90°，∴∠1+∠2=90°，∠1=90°-∠2不一定等于30°，故D不一定成立.
故答案为：D.
先求出∠2+∠4=90°，再对每个选项一一判断求解即可。
14. D
考点:含30°角的直角三角形，旋转的性质
解：设CD与B′C′相交于点O，连接OA．
根据旋转的性质，得∠BAB′＝30°，则∠DAB′＝60°．
在Rt△ADO和Rt△AB′O中，AD＝AB′，AO＝AO，
∴Rt△ADO≌Rt△AB′O．
∴∠OAD＝∠OAB′＝30°．
又∵AD＝1，
∴OD＝AD?tan∠OAD＝ ．
∴公共部分的面积＝2× × ×1＝1× ＝ ．
故答案为：D．

只需把公共部分分割成两个三角形，根据旋转发现两个三角形全等，从而求得直角三角形的边，再进一步计算其面积。
15. D
考点:三角形内角和定理，含30°角的直角三角形
∵在△ABC中，∠C＝60°，AD是BC边上的高，
∴∠DAC＝180°﹣∠C﹣∠ADC＝180°﹣60°﹣90°＝30°，
∵∠AFB＝90°，EF＝2，
∴AE＝2EF＝4，
∵点E为AD的中点，
∴DE＝AE＝4，
∵∠C＝60°，∠BFC＝180°﹣90°＝90°，
∴∠EBD＝30°，
∴BE＝2DE＝8，
∴BF＝BE＋EF＝8＋2＝10，
故答案为：D．
根据三角形内角和定理求出∠DAC＝30°和∠EBD＝30°，根据含30°角的直角三角形的性质得出AE＝2EF，BE＝2DE，代入求出即可．
二、填空题
16. 50
考点:等腰三角形的性质，含30°角的直角三角形，平行四边形的性质，角平分线的定义
解：过点E作EF⊥BC，垂足为F，
∵∠EBC=30°，BE=10，
∴EF= BE=5，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DEC=∠BCE，
又EC平分∠BED，即∠BEC=∠DEC，
∴∠BCE=∠BEC，
∴BE=BC=10，
∴四边形ABCD的面积= = =50，
故答案为：50.
过点E作EF⊥BC，垂足为F，由含30°角的直角三角形的性质得出EF= BE=5，根据平行四边形的性质及角平分线的定义得出∠BCE=∠BEC，从而可得BE=BC=10，由平行四边形ABCD的面积= ， 据此计算即可.
17. 5
考点:角平分线的性质，含30°角的直角三角形
作DH⊥AB于H，
∠DEH=∠DBE+∠BDE=30°，
∴DH= DE=5，
∵DE∥BC，
∴∠DBF=∠BDE，
∴∠DBF=∠DBH，又DF⊥BC，DH⊥AB，
∴DF=DH=5，
故答案为：5．

作DH⊥AB于H，由△BED是等腰三角形可知DE=BE=10,∠DEA=30°，在△DEH中根据30°角直角三角形的性质可得DH=5，再根据平行+等腰可得BD是∠ABC的平分线，根据角平分线的性质可得DF=DE=5.
18. 126°
考点:平行线的性质，直角三角形的性质
解：∵a∥b，
∴∠3=∠1=36°，
∵c⊥d，
∴∠4=90°，
∵∠2=∠3+∠4，
∴∠2=126°，
故答案为：126°.
根据两直线平行，同位角相等，求得∠3=36°，根据垂直的定义，求得∠4=90°，利用∠2=∠3+∠4求解即可
19. 120
考点:等腰三角形的性质，轴对称的性质，直角三角形的性质
解：由折叠性质得： AB'=AB，∠B'AB=∠BAC=40°，
∴∠ABB'=∠AB'B= ，
∵ ∠C=90°，∠BAC=40°，
∴∠ABC=50°，
∴ ∠B'BC= ∠ABC+∠ABB'=50°+70°=120°.
根据折叠的性质得出AB'=AB，∠B'AB=∠BAC=40°，再根据等腰三角形的性质得出∠ABB'=70°，再根据直角三角形两个锐角互余得出∠ABC=50°，利用∠B'BC= ∠ABC+∠ABB'，即可得出答案.
20. 99
考点:直角三角形的性质
解：根据题意可得，∠BCD=60°，∠ACD=37°，CD⊥AB，CD=40
在直角三角形BCD中，tan∠BCD=
∴BD=CD×tan∠BCD=40≈69.2
在直角三角形ACD中tan∠ACD=
∴AD=CD×tan∠ACD≈40×0.75=30
∴AB=BD+AD≈69.2+30=99
根据直角三角形的性质以及应用，计算得到答案即可。
21. 2
考点:含30°角的直角三角形，等腰直角三角形
解：∵BC⊥AE，DE⊥AE
∴BC∥DE
∴∠AFC=∠D=45°
∴△AFC为等腰直角三角形
∴AC=FC
设AC=FC=x，则 ， 解得x=1，即AC=FC=1
在Rt△ABC中，∠B=30°
∴AB=2AC=2。
考查等腰直角三角形与含30°角的直角三角形的性质，先根据平行线的性质确定∠AFC为45°，判定△AFC为等腰直角三角形，然后利用勾股定理计算出AC，再在△ABC中利用30°的角所对的直角边是斜边的一半，计算出AB。
22. 35°
考点:等腰三角形的性质，直角三角形的性质
解：∵ 在△ABC中，∠ACB=90°．CD为AB边上的中线， ∠A?=55°
∴CD=AD=BD
∴∠DCA=∠A=55°
∴∠BCD=90°-55°=35°。
故答案为：35°.
考查直角三角形斜边中线的性质以及等腰三角形的性质，直角三角形斜边中线等于斜边的一半，判定出△ACD和△BCD都是等腰三角形，然后再利用三角形内角和计算即可。
23. 9
考点:等腰三角形的性质，含30°角的直角三角形
解：∵AB＝AC，∠BAC＝120°，
∴∠B＝∠C＝30°，
∵AD⊥AC，
∴∠DAC＝90°，又∠C＝30°，
∴CD＝2AD＝6，
∵∠BAC＝120°，∠DAC＝90°，
∴∠BAD＝30°，
∴∠DAB＝∠B，
∴BD＝AD＝3，
∴BC＝BD+CD＝9，
故答案为：9．
先求出∠B＝∠C＝30°，再求出∠DAB＝∠B，最后计算求解即可。
24. 75
考点:三角形的外角性质，直角三角形的性质，对顶角及其性质
解：如图，
∵∠2＝90°﹣45°＝45°（直角三角形两锐角互余），
∴∠3＝∠2＝45°，
∴∠1＝∠3+30°＝45°+30°＝75°.
故答案为：75。
根据学具的性质及直角三角形两锐角互余得出∠2=45°，进而根据对顶角相等得出∠3=45°，然后利用三角形的外角定理，由∠1=∠3+30°即可算出答案。
25.
考点:垂线段最短，等边三角形的性质，直角三角形的性质
如图，过点O作OM⊥AB，垂足为M，连接AO并延长交BC于点N，
∵点O是等边△ABC的∠B和∠C的角平分线的交点，
∴ON⊥BC，OM=ON，∠MAO=30°，∠MOA=60°，
∴∠DOM+∠DON=120°，
∵∠DOE=120°，
∴∠NOE+∠DON=120°，
∴∠DOM=∠NOE，
∴Rt△DOM≌Rt△NOE，
∴DO=OE，∠ODE=30°，
过点O作OH⊥DE，垂足为H，
∴OH= ，DH=HE= ，
∴△ODE的周长为2DO+ DO=（ ）DO，
∴△ODE的周长要想取最小值，只需DO最小，
根据垂线段最短，当OD=OM时，DO最小，周长最小，
∵∠MAO=30°，OA=2，
∴OM=1，
∴△ODE的周长最小为 .
故答案为： .

过点O作OM⊥AB，垂足为M，连接AO并延长交BC于点N，过点O作OH⊥DE，垂足为H，由已知易证Rt△DOM≌Rt△NOE，则DO=OE，∠ODE=30°，由30度角所对的直角边等于斜边的一半可得OH=OD，由等腰三角形三线合一可得DH=HE，因为△ODE的周长=DO+EO+DE=2DO+2DH=（2+）DO，所以要使三角形ODE的周长最小，只需DO最小即可，根据垂线段最短，当OD=OM时，DO最小，周长最小可求解.
三、计算题
26. （1）解：∵AB=AC，AD⊥BC于点D
∴∠BAD=∠CAD，∠ADC=90°，又∠C=42°.
∴∠BAD=∠CAD=90°-42°=48°
（2）证明：∵AB=AC，AD⊥BC于点D，
∴∠BAD=∠CAD
∵EF∥AC，
∴∠F=∠CAD
∴∠BAD=∠F，∴AE=FE
考点:等腰三角形的性质，直角三角形的性质
（1）根据等腰三角形的三线合一得到∠BAD＝∠CAD，再根据直角三角的两锐角互余即可得出∠BAD＝∠CAD＝90°﹣42°＝48°；
（2）根据等腰三角形的三线合一得到∠BAD＝∠CAD，根据二直线平行内错角相等得到∠F＝∠CAD，由等量代换得到∠BAD＝∠F，根据等角对等边得出结论。

?
四、解答题
27. 解：∵ EF⊥AB于F，
∴ ∠B+∠BEF=90°，
∵ ∠AGH=∠B， ∠CGH=∠BEF，
∴ ∠AGH+∠CGH =90°，
即∠CGA =90°，
∴ CG⊥AB.
考点:垂线，直角三角形的性质
根据垂直的定义得出∠B+∠BEF=90°，再根据题意得出∠AGH+∠CGH =90°，即可得出CG⊥AB.
28. 解：∵△ABC是等边三角形，
∴∠B=∠ACB= 60° ,
∵DE∥AB，
∴ ∠EDC=∠B= 60°,
∴△EDC是等边三角形，
∴DE= DC= 2 ，
在Rt△DEF中，∠DEF= 90° ,
∵DE=2，∠F= 30°,
∴DF= 2DE= 4，
∴ EF===?2 ，
故答案为：2.
考点:等边三角形的性质，含30°角的直角三角形
先证明△DEC为等边三角形，再在Rt△DEC中根据含30°角的等腰直角三角形的性质求出DF，最后由勾股定理求出EF即可.
29. 解：∵AD平分∠BAC，∴∠EAD＝∠CAD.
∵∠ACB＝90°，DE⊥AB，∴∠ACD＝∠AED.
又∵AD＝AD，∴△ACD≌△AED.
∴AE＝AC.
∵∠ACB＝90°，∠B＝30°，∴∠BAC＝60°.
∴△ACE为等边三角形，?? ∴CE＝AC＝3.
考点:含30°角的直角三角形，直角三角形斜边上的中线
只要证明 为特殊三角形，则 的长度可求，因为 ，猜测 为等边三角形，只要 即可，而通过已知条件可知 ，所以 ，则 为等边三角形， 的长度可求.
五、综合题
30. （1）证明：在等腰Rt△ABC中，
∵点D为斜边AB上的中点
∴CD= AB，CD⊥AB
∵AD= AB
∴AD=CD
∵CD⊥AB
∴∠ADG=∠CDE=90°
∵AH⊥CE
∴∠CGH+∠GCH=90°
∵∠AGD+∠GAD=90°
又∵∠AGD=∠CGH
∴∠GAD=∠GCH
在△△ADG和△CDE中
∵∠ADG=∠CDE=90°,AD=CD,∠GAD=∠GCH
∴△ADG≌△CDE
（2）解：∵AH⊥CE，点H为CE的中点
∴AC=AE
∴∠CAH=∠EAH
∵∠CAH+∠AFC=90°
∠EAH+∠AGD=90°
∴∠AFC=∠AGD
∵∠AGD=∠CGH
∴∠AFC=∠CGH
即∠CGF=∠CFG
考点:全等三角形的判定与性质，线段垂直平分线的性质，直角三角形斜边上的中线
（1）由于△ACB是等腰直角三角形，结合D是斜边BC的中点，可得AD和BD相等，AD垂直CD，再根据同角的余角相等可得 ∠GAD=∠GCH ，于是利用角角边定理可证△ADG≌△CDE.
（2）由垂直平分线的性质可得AC=AE ， 于是可得∠CAH=∠EAH，?再由等角的余角相等可知 ∠AFC=∠AGD，?再结合对顶角相等，最后等量代换即可证得∠CGF=∠CFG .
31. （1）1.5
（2）解：∵∠B=60°，
∴当∠PQB为直角时，PB=2QB，
则AB-AP=2BQ，
3-t=2t,
解得t=1,
当∠BPQ为直角时，
BQ=2PB，
则BQ=2(AB-AP)
即t=2(3-t),
解得x=2.
∴当t 为 2s 或 1s 时，△PBQ 为直角三角形.
（3）解：当△DCQ为等腰三角形时，
∵∠DCQ=120°，
∴CD=CQ，
∴∠CQD=∠ACB=30°，
∴∠BPQ=90°，
∴BQ=2BP，
∴3+t=2(3-t),
解得t=1.
（4）解：如图，过P作PE∥BC，
∵△ABC为等边三角形，
∴△APE为等边三角形，
∴PE=AP=t,
∵CQ=t,
∴PE=CQ，
∴四边形PCQE是平行四边形，
∴PD=QD，
∵△PCD和△QCD等底同高，
∴ S△PCD=S△QCD .

考点:三角形的面积，等边三角形的性质，含30°角的直角三角形
解：（1）∵△ABC是等边三角形，
∴当P为AB的中点时，CP⊥AB，
∴AP=1.5，
∴t=1.5÷1=1.5(s).
（1）根据等边三角形的性质，得出当P为AB的中点时，CP垂直AB，再用速度公式求时间即可；
（2） △PBQ是直角三角形有两种情况，因∠B=60°，当PQ垂直BC时，BP=2BQ，当QP垂直AB时，BQ=2BP，分别根据这两种情况列式求出时间即可；
（3）当△DCQ为等腰三角形时，由三角形的外角的性质，结合∠ACB等于60°，可得∠DQC为30°，从而根据30°角所对的直角边等于斜边的一半列式即可求解；
（4）过P作PE∥BC，由等边三角形的性质，结合AP=CQ，得出四边形PCQE是平行四边形，则对角线互相平分，可知PD=QD，然后由两个三角形等高同底得出其面积相等.
_21?????????è?????(www.21cnjy.com)_