直线与圆的位置关系1

(共14张PPT)
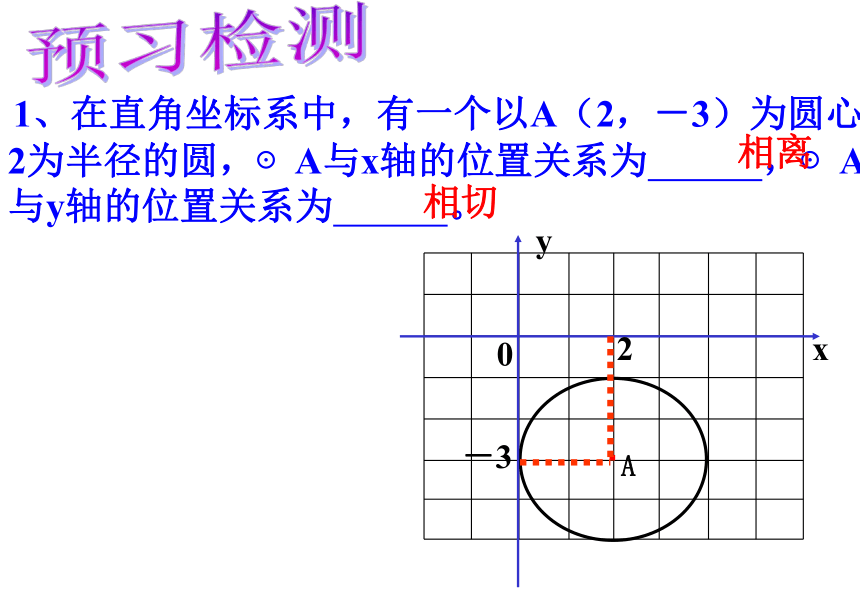
1、在直角坐标系中，有一个以A（2，－3）为圆心，2为半径的圆，⊙A与x轴的位置关系为 ，⊙A与y轴的位置关系为 。
相切
相离
　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　
　 　 　 　 　 　 　 　
·
－3
0
2
y
x
A
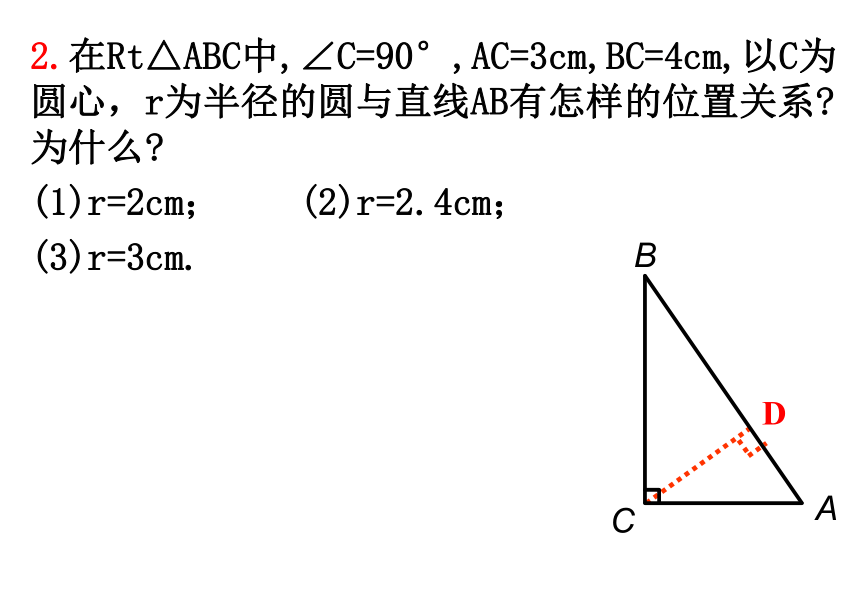
2.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心，r为半径的圆与直线AB有怎样的位置关系 为什么
(1)r=2cm； (2)r=2.4cm；
(3)r=3cm.
D
B
C
A
D
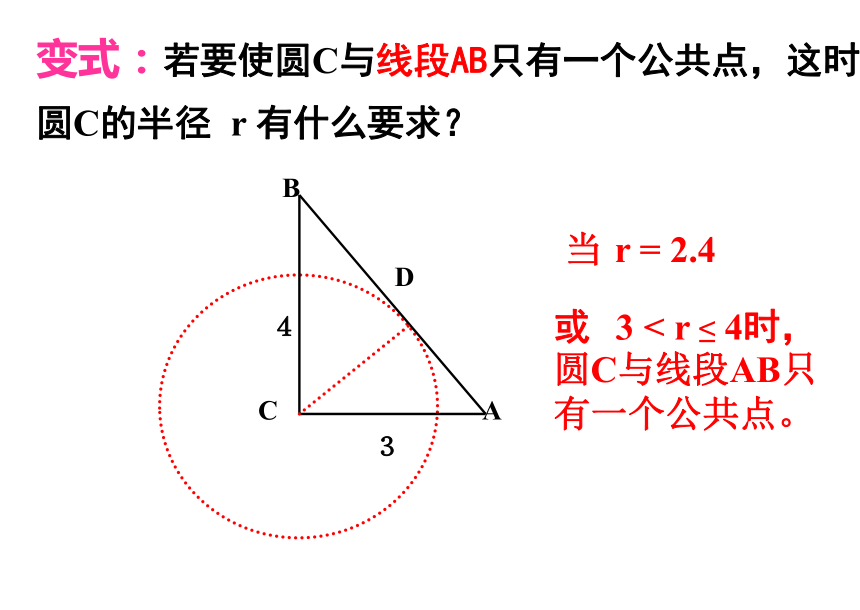
变式：若要使圆C与线段AB只有一个公共点，这时圆C的半径 r 有什么要求？
３
４
当 r = 2.4
或 3 < r ≤ 4时，圆C与线段AB只有一个公共点。
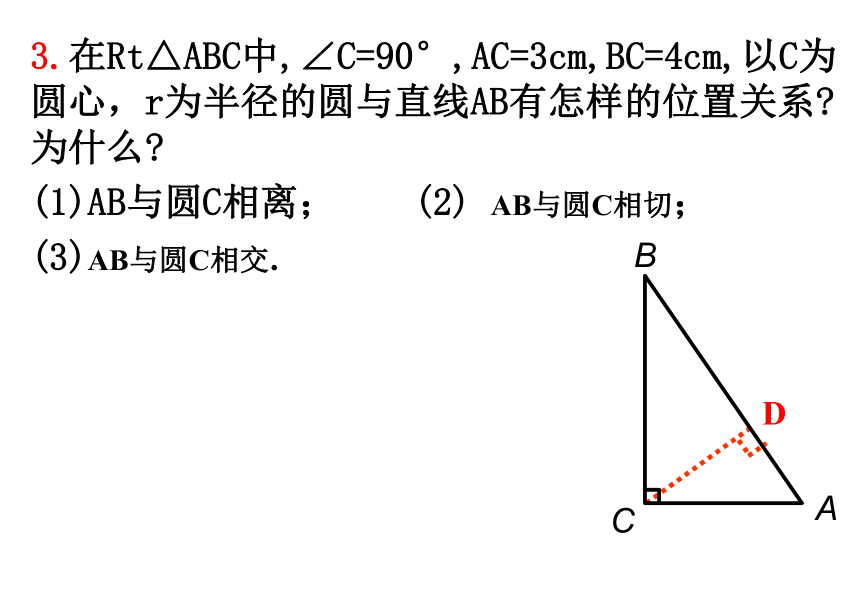
3.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心，r为半径的圆与直线AB有怎样的位置关系 为什么
(1)AB与圆C相离； (2) AB与圆C相切；
(3)AB与圆C相交.
D
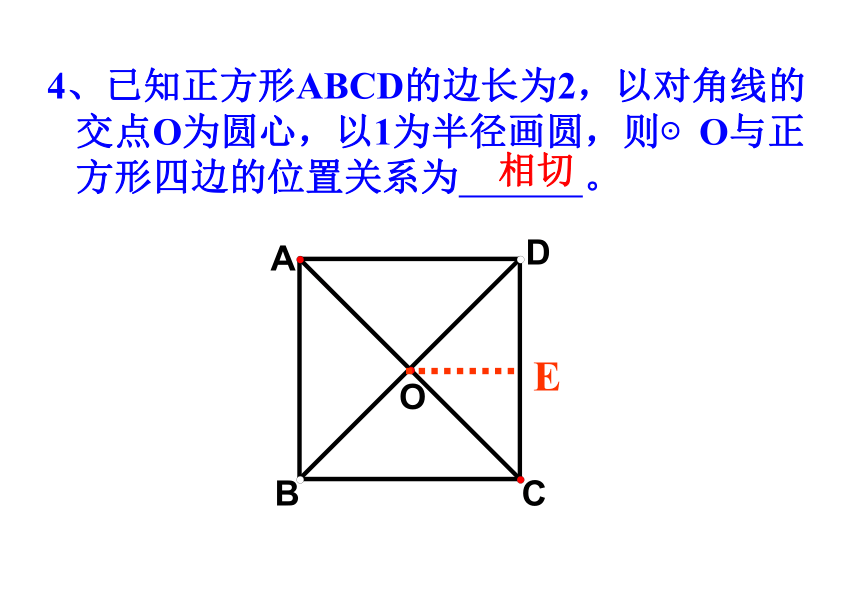
4、已知正方形ABCD的边长为2，以对角线的交点O为圆心，以1为半径画圆，则⊙O与正方形四边的位置关系为 。
相切
E
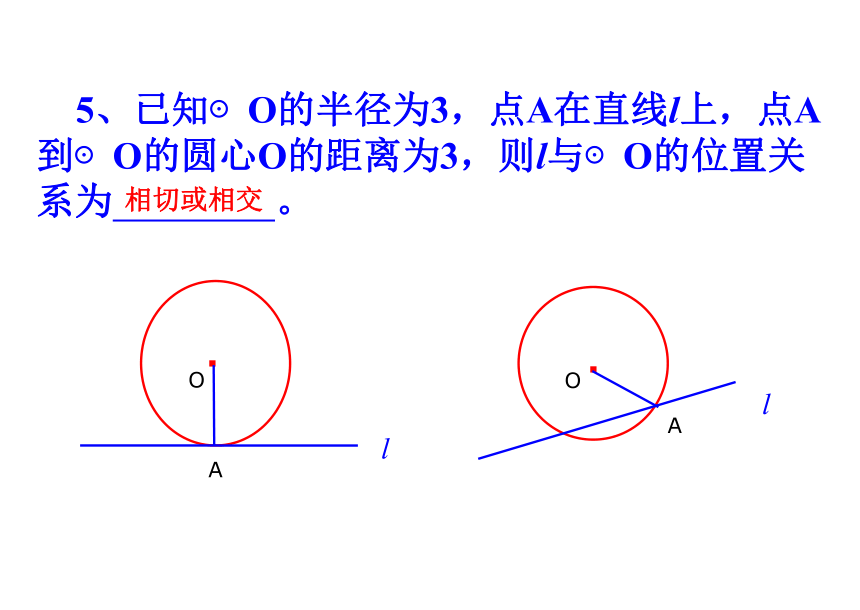
5、已知⊙O的半径为3，点A在直线l上，点A到⊙O的圆心O的距离为3，则l与⊙O的位置关系为 。
相切或相交
·
·
O
O
A
A
l
l
当堂练习
已知圆O的半径为r，点O到直线L的距离为d，且
|d-3|+(6-2r)2=0.试判断直线L与圆O的位置关系.
如图，直线AB，CD相交于点O，∠AOC=30°，半径为1cm的○P的圆心在 射线OA上，开始时，PO=6cm，若圆P以1cm/s的速度沿AB方向移动，则当圆P的运动时间t（s）满足_______条件时，圆P与直线CD相切.
P
O
A
B
C
D
直
相交
如图，一平面内，已知点O到直线L的距离是5，以点O为圆心，r为半径画圆.
（1）当r=______时，圆O上有且只有一个点到直线L的距离等于3；
（2）当r=______时，圆O上有且只有三个点到直线L的距离等于3；
（3）随着r的变化，圆O上到直线L的距离等于3的点的个数有哪些变化？求出相应的r值或取值范围（不必写出据算过程）。
O
L
思考：如图,公路MN和PQ在P处交汇, 且∠QPN=300 , 点A处有一所中学, AP=160米, 假设拖拉机沿PN行使时, 周围100米以内会受到噪音的影响, 已知拖拉机的速度为18千米／时, 那么学校会受到影响吗 如果会, 受到影响的时间多长
M
N
P
Q
A
3.如图，在码头A的北偏东60°方向有一个海岛，离该岛中心P的8海里范围内是一个暗礁区。货船从码头A由西向东方向航行，行驶了18海里到达B，这时岛中心P在北偏东30°方向。若货船不改变航向，问货船会不会进入暗礁区？
直线与圆的位置
公共点个数
d与r的关系
公共点名称
直线与圆的三种位置关系
2
1
0
dd=r
d>r
交点
切点
无
相交
相切
相离
布置作业：
1、必做题：教材P502、3
2、选做题：教材 P505
3、课后思考题。