圆心角的习题课

(共25张PPT)
习题目标:熟练运用圆心角定理及其逆定理
1.已知等边三角形ABC的边长为 cm,求它的外接圆的半径。
判断：
1、等弦所对的弧相等。 （ ）
2、等弧所对的弦相等。 （ ）
3、圆心角相等，所对的弦相等。( ）
4、弦相等，所对的圆心角相等。（ ）
×
×
×
√
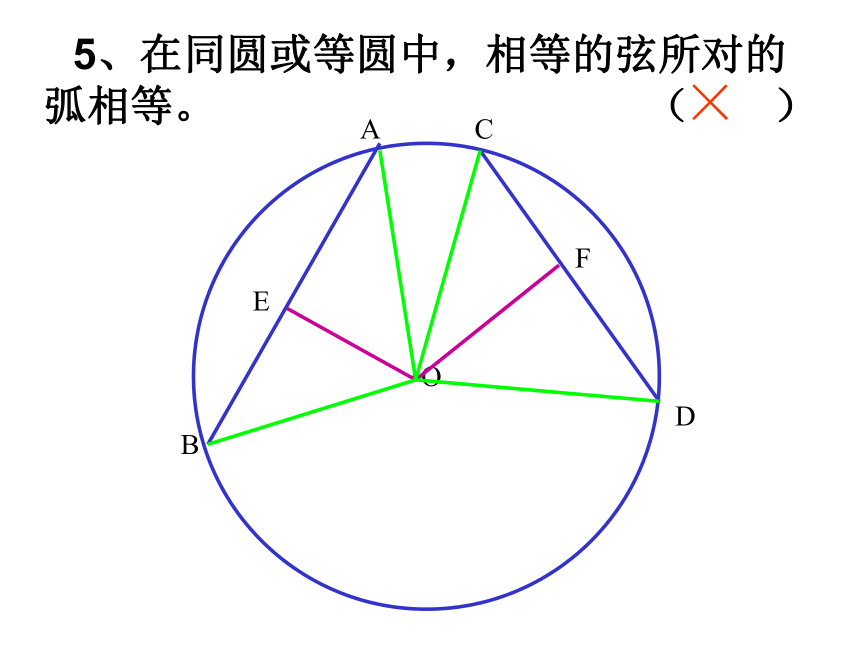
O
A
B
C
D
E
F
5、在同圆或等圆中，相等的弦所对的弧相等。 （ ）
×
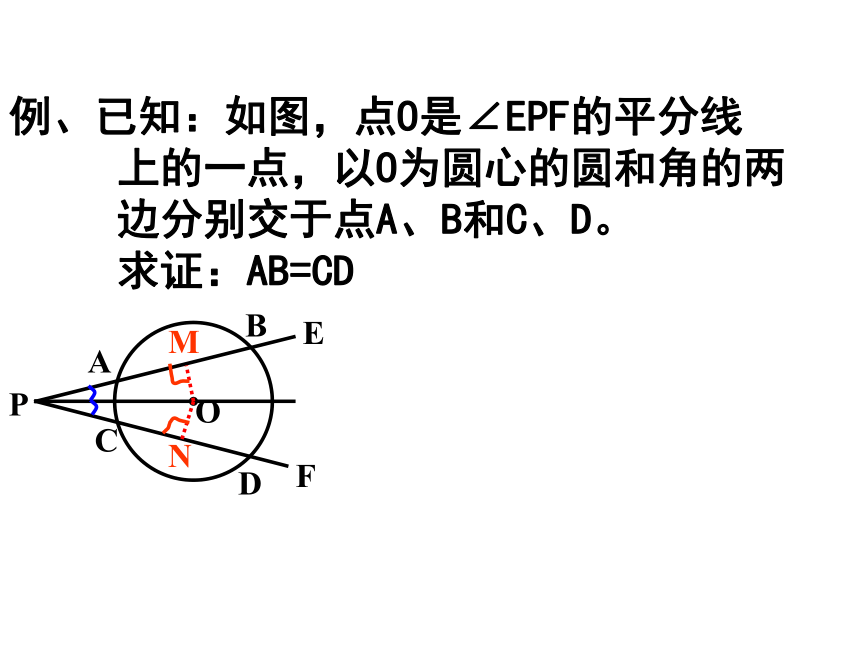
例、已知：如图，点O是∠EPF的平分线
上的一点，以O为圆心的圆和角的两
边分别交于点A、B和C、D。
求证：AB=CD
P
O
A
F
E
D
C
B
M
N
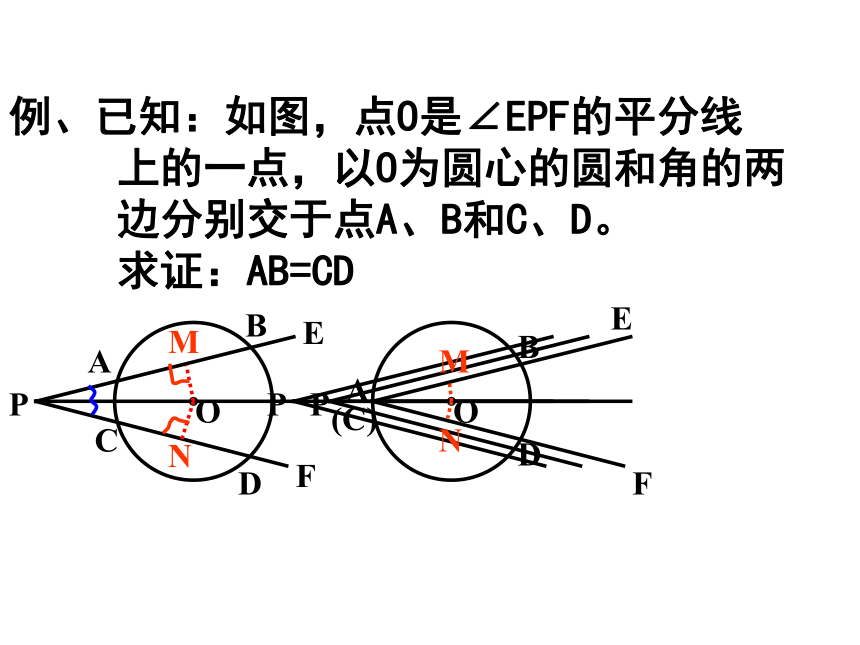
例、已知：如图，点O是∠EPF的平分线
上的一点，以O为圆心的圆和角的两
边分别交于点A、B和C、D。
求证：AB=CD
P
O
A
F
E
D
(C)
B
P
P
O
A
F
E
D
C
B
M
N
M
N
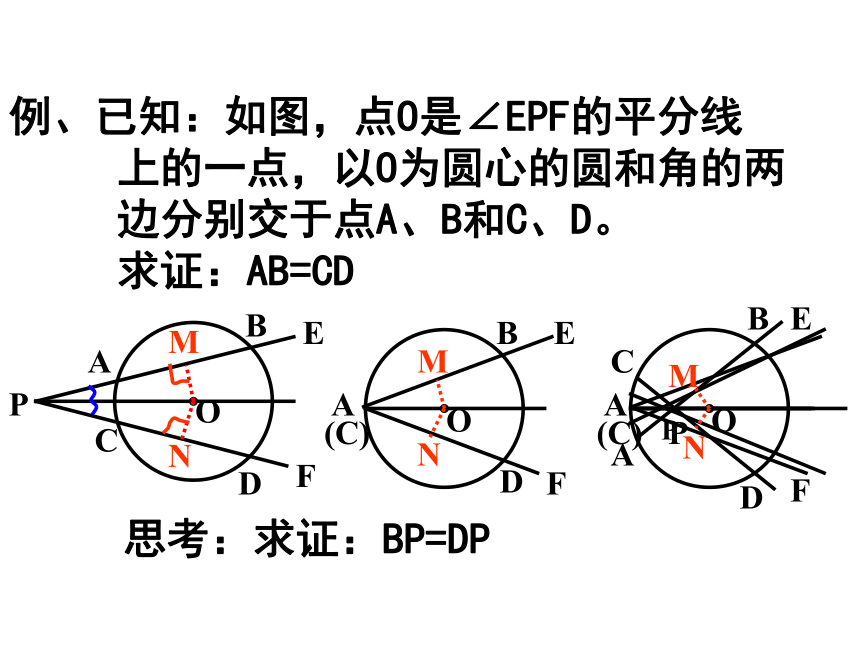
例、已知：如图，点O是∠EPF的平分线
上的一点，以O为圆心的圆和角的两
边分别交于点A、B和C、D。
求证：AB=CD
O
A
F
E
D
(C)
B
P
O
A
F
E
D
C
B
M
N
O
A
(C)
F
E
B
P
C
A
D
P
思考：求证：BP=DP
M
N
M
N
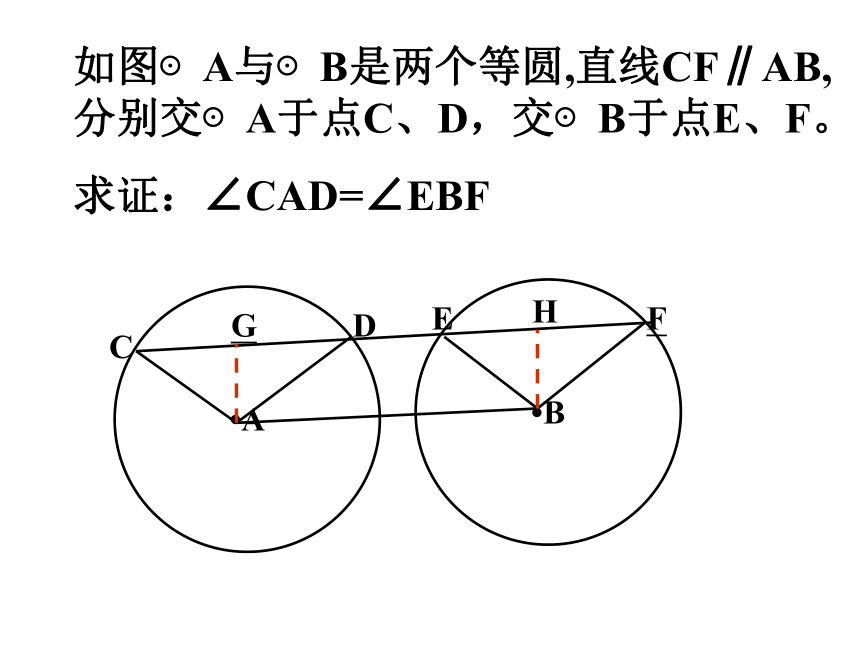
如图⊙A与⊙B是两个等圆,直线CF∥AB,分别交⊙A于点C、D，交⊙B于点E、F。
求证：∠CAD=∠EBF
A
B
C
D
E
F
G
H

A
B
C
D
M
N
O
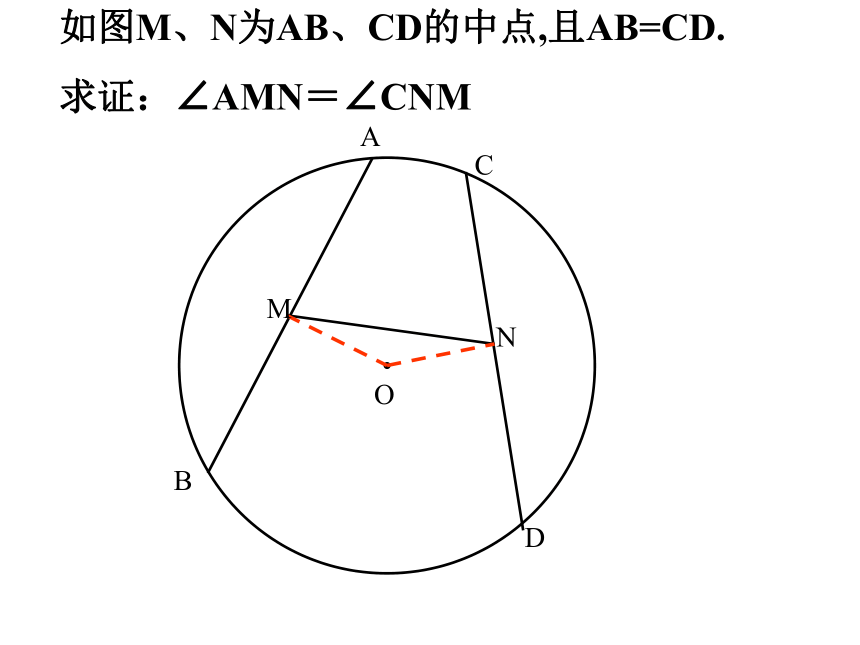
如图M、N为AB、CD的中点,且AB=CD.
求证：∠AMN＝∠CNM
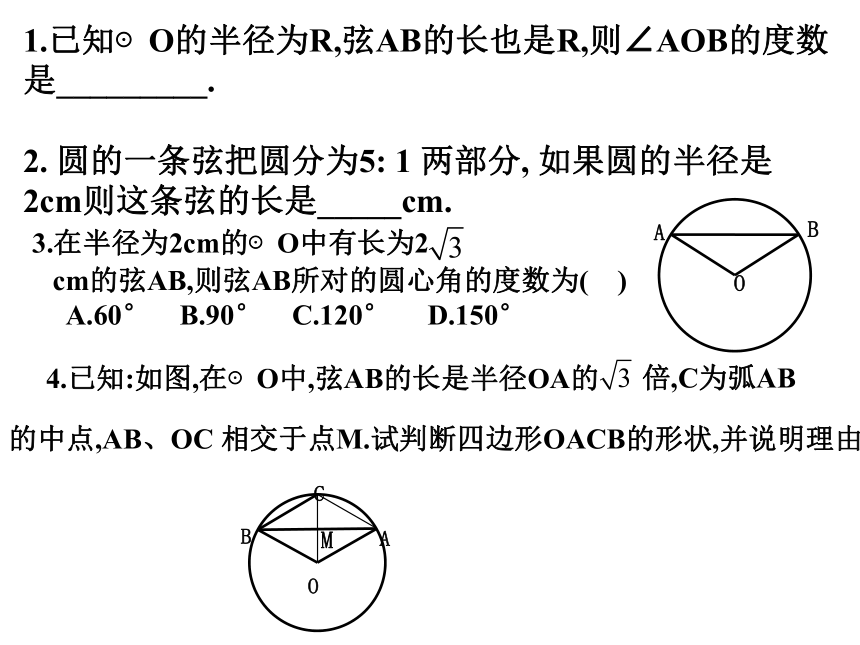
1.已知⊙O的半径为R,弦AB的长也是R,则∠AOB的度数是_________.
2. 圆的一条弦把圆分为5: 1 两部分, 如果圆的半径是2cm则这条弦的长是_____cm.
3.在半径为2cm的⊙O中有长为2
cm的弦AB,则弦AB所对的圆心角的度数为( )
A.60° B.90° C.120° D.150°
4.已知:如图,在⊙O中,弦AB的长是半径OA的
倍,C为弧AB
的中点,AB、OC 相交于点M.试判断四边形OACB的形状,并说明理由.
M
C
B
A
O
B
A
O
5.如图,AB是⊙O的直径,P是AB上一点,C、D分别是圆上的点,且∠CPB=∠DPB,弧
,试比较线段PC、PD的大小关系.
6点A是半圆上的三等分点,B是弧NA的中点,P是直径MN上一动点.⊙O的半径为1,问P在直线MN上什么位置时,AP+BP的值最小 并求出AP+BP的最小值.
N
M
B
P
A
O
D
C
B
P
A
O
垂径定理及逆定理
如图,在下列五个条件中:
只要具备其中两个条件,就可推出其余三个结论.
●O
A
B
C
D
M└
⌒
⌒
⑤AD=BD.
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC=BC,
回顾
垂直于弦的直径平分这条弦，并且平分弦所对的弧．
1、平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧.
2、平分弧的直径垂直平分弧所对的弦。
垂径定理的应用：作图；计算和证明．
（2）半径（r)、半弦、弦心距(d)组成的直角三角形是研究与圆有关问题的主要思路，它们之间的关系：
（1）画弦心距是圆中常见的辅助线；
．
O
A
B
C
r
d
1．已知⊙0的半径为13，一条弦的AB的弦心距为5，则这条弦的弦长等于 ．
24
2．如图，AB是⊙0的中直径，CD为弦，CD⊥AB于E，则下列结论中不一定成立的是（ ）
A．∠COE=∠DOE B．CE=DE
C．OE=BE D．BD=BC
⌒
⌒
C
．
A
B
C
O
D
E
练习：
3．过⊙O内一点M的最长弦长为10cm，最短弦长为8cm，那么OM长为（ ）
A．3 B．6cm C． cm D．9cm
4．如图，⊙O的直径为10，弦AB长为8，M是弦AB上的动点，则OM的长的取值范围是（ ）
A．3≤OM≤5 B．4≤OM≤5
C．3．
A
B
O
M
A
A
练习：
5． 已知⊙O的半径为10，弦AB∥CD，AB=12，CD=16，则AB和CD的距离为 ．
6．如图，已知AB、AC为弦，OM⊥AB于点M， ON⊥AC于点N ，BC=4，求MN的长．
2或14
．
A
C
O
M
N
B
思路：由垂径定理可得M、N分别是AB、AC的中点，所以MN= BC=2．
7.已知 ⊙O的半径为1,弦AB、AC的长分别是
和 ， 求∠BAC的度数.
船能过拱桥吗
2 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？
相信自己能独立完成解答.
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
在Rt△OAD中，由勾股定理，得
解得 R≈3.9（m）.
在Rt△ONH中，由勾股定理，得
∴此货船能顺利通过这座拱桥.
挑战自我画一画
如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
圆心角定理的推论
在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
┓
D
●O′
A′
B′
D′
┏
例1 如图，△ABC是等边三角形，以BC为直径画⊙O交AB，AC于点D，E，
求证：BD=CE
例2 如图，OA、OB、OC是⊙O的三条半径，AC=BC，M、N分别是OA、OB的中点，试问∠MCO和∠NCO有什么关系？说明理由。
例2 如图，∠AOB=2∠COD，则
AB=2CD吗？
⌒
AB=2CD吗？
⌒
.
A
B
C
P
O
例3、当BA=AC，∠CAB= 60° ，且当P为CB
的中点时，求证：PC=PB= PA
例4、 如图， ⊙O 的两条弦AB和CD相交于点P，且PD=PB，则AB=CD吗？
例1.如图,把Rt△ABC的斜边放在直线l上，按顺时针方向在l上转动２次，使它转到△A２B２C２的位置.设BC=1,AC=
求(1)点A所经过的路线长.
(2)点A所经过的路线与直线l所围成的面积．