3.4圆周角（1）

(共17张PPT)
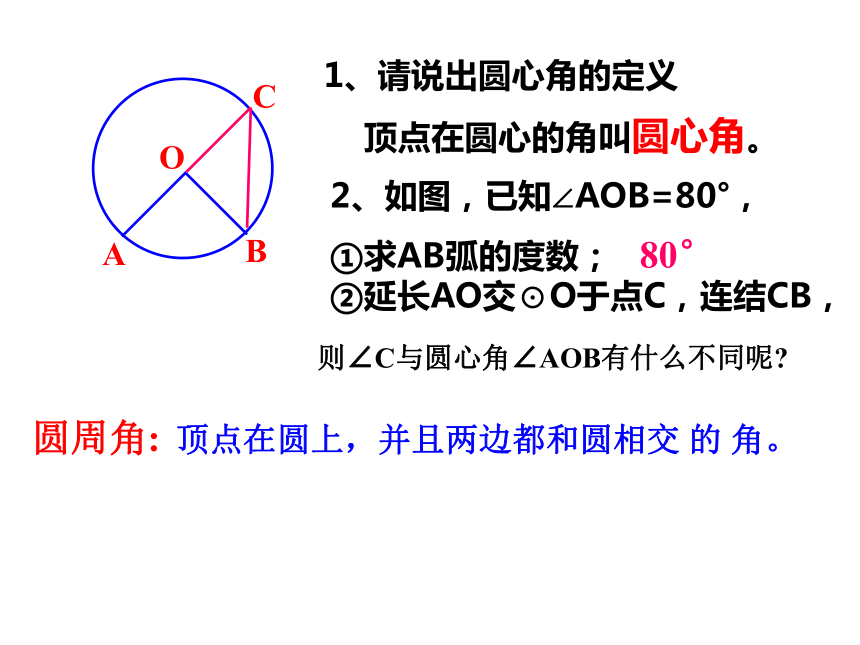
O
A
B
1、请说出圆心角的定义
顶点在圆心的角叫圆心角。
2、如图，已知∠AOB=80°，
①求AB弧的度数；
②延长AO交⊙O于点C，连结CB，
C
80°
顶点在圆上，并且两边都和圆相交 的 角。
圆周角:
则∠C与圆心角∠AOB有什么不同呢
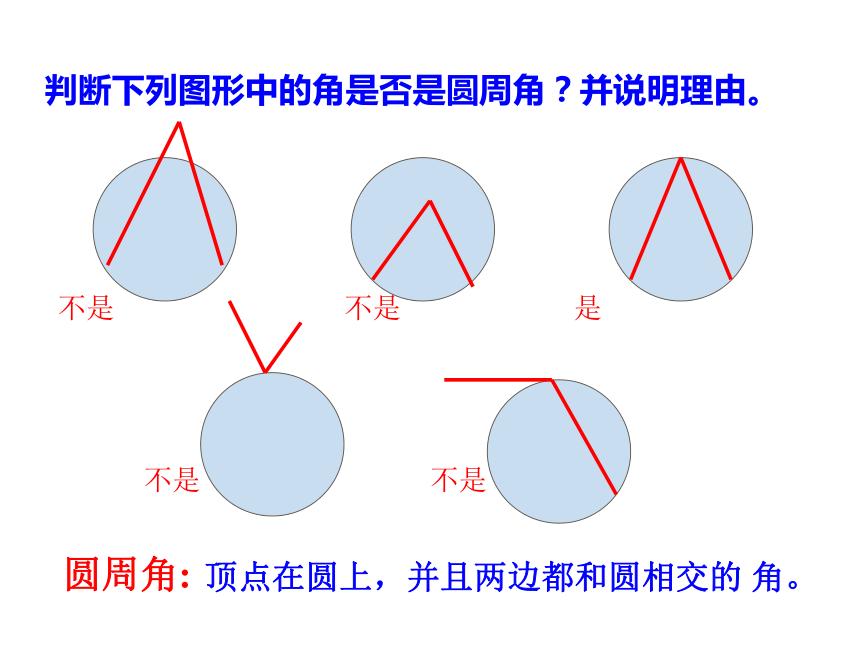
判断下列图形中的角是否是圆周角？并说明理由。
不是
不是
是
不是
不是
顶点在圆上，并且两边都和圆相交的 角。
圆周角:
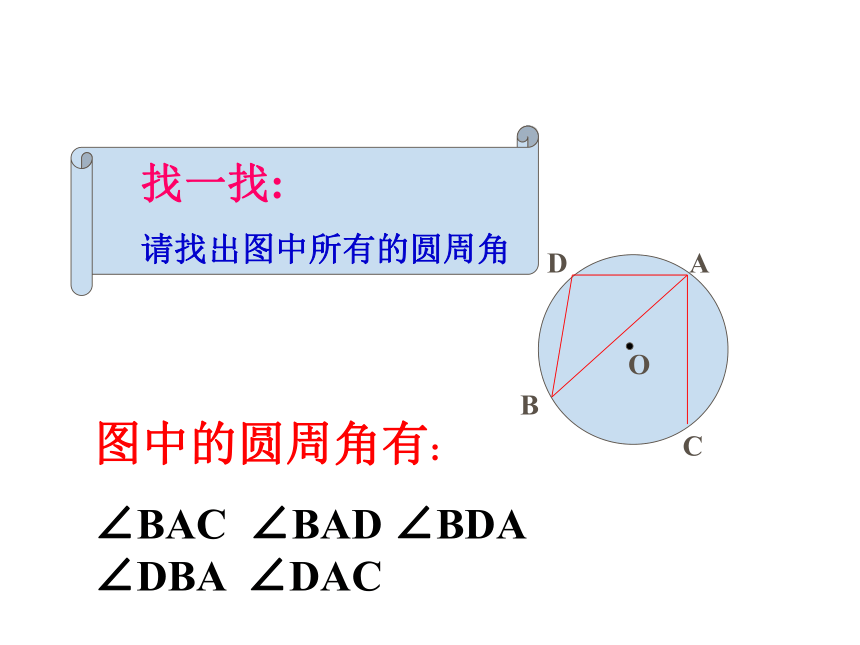
A
B
C
D
找一找:
请找出图中所有的圆周角
图中的圆周角有:
∠BAC ∠BAD ∠BDA ∠DBA ∠DAC
O
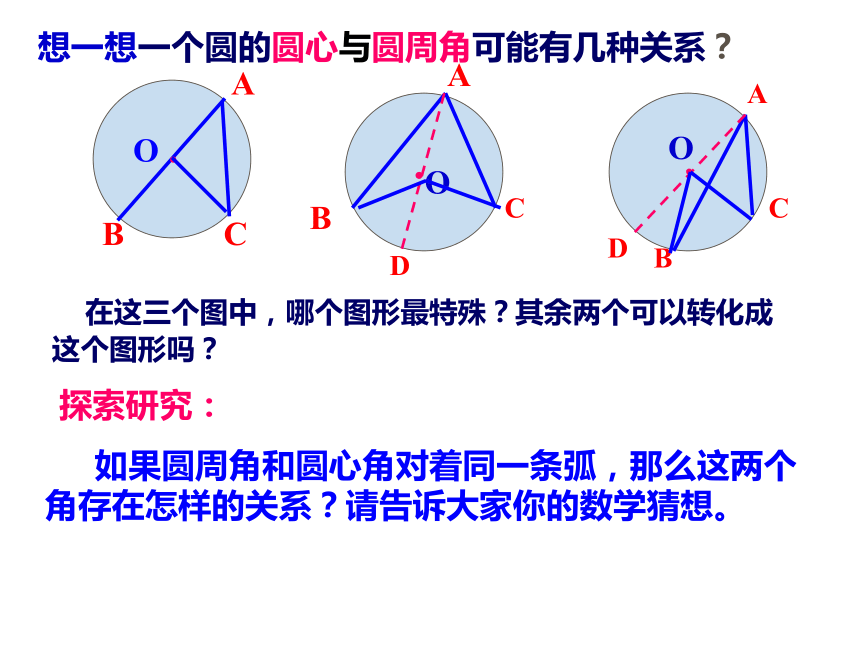
想一想；
一个圆的圆心与圆周角在位置上可能有几种关系？请大家在练习本上画一画.
A
B
C
O
想一想一个圆的圆心与圆周角可能有几种关系？
.
在这三个图中，哪个图形最特殊？其余两个可以转化成这个图形吗？
A
B
C
.
D
O
C
O
A
B
D
.
探索研究：
如果圆周角和圆心角对着同一条弧，那么这两个角存在怎样的关系？请告诉大家你的数学猜想。
C
A
B
O
A
B
C
O
D
B
C
O
A
D
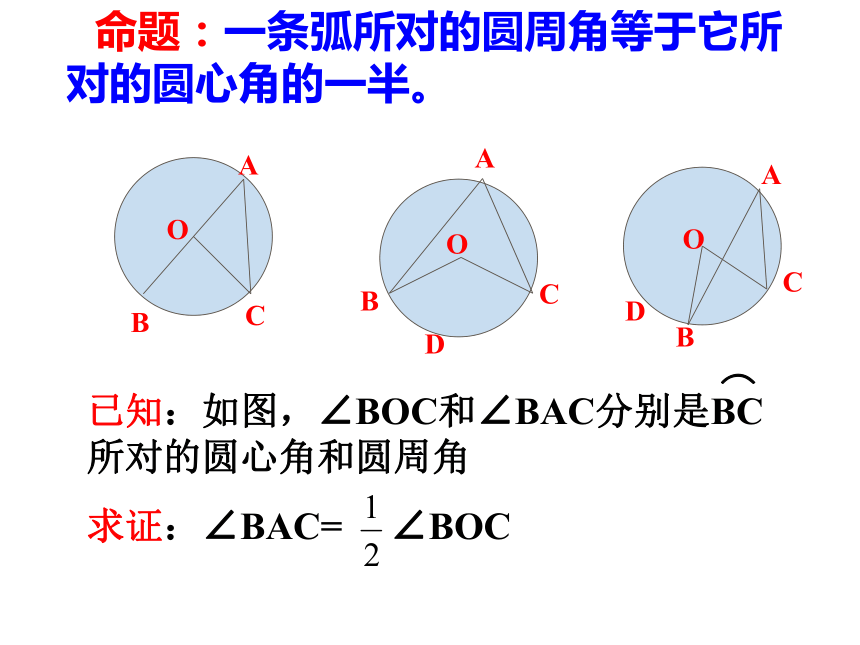
已知：如图，∠BOC和∠BAC分别是BC所对的圆心角和圆周角
求证：∠BAC= ∠BOC
⌒
命题：一条弧所对的圆周角等于它所对的圆心角的一半。
A
B
O
C
证明：（1）当圆心O在圆周角∠BAC的一边AB上时
∵OA=OC
∴∠BAC=∠C
∵∠BOC是△OAC的外角
∴∠BOC=∠C+∠BAC
=2∠BAC
∴∠BAC= ∠BOC
B
A
C
D
O
(2)当圆心O在圆周角∠BAC的内部时,过点A作直径AD
由(1)得∠BAD= ∠BOD
∠DAC= ∠DOC
∴ ∠BAD+ ∠DAC= (∠BOD + ∠DOC)
即: ∠BAC= ∠BOC
B
A
C
D
O
(3)当圆心O在∠BAC的外部时,过点A作直径AD,则由(1)得
∠DAC= ∠DOC ∠DAB= ∠DOB
∴ ∠DAC--∠DAB= (∠DOC -- ∠DOB)
即:∠BAC= ∠BOC
圆周角定理：
一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角的度数等于它所对弧的度数的一半。
A
B
C
O
∵∠BAC和∠BOC都对BC
∴∠BAC= ∠BOC
⌒
A
B
C
O
1、如图，已知在⊙ O 中，∠BOC =150°，求∠A
2、已知一条弧所对的圆周角等于500，则这条弧所对的圆心角是多少度？
3、已知一条弧的度数为400，求这条弧所对的圆心角和圆周角的度数。
4、一条弧所对的圆心角的度数为950，求这条弧的度数和它所对的圆周角的度数。
此图，弧ADB所对的圆心角是？几度？
圆周角又是谁？几度呢？
∠AOB
180°
圆周角定理的推论：
（或直径半圆）所对的圆周角是直角；90°的圆周角所对的弦是直径。
·
O
C
A B
D
∠ACB
90 °
O
A
C
B
想一想：
1、已知：∠AOB=100°，求∠ACB的度数
2、若圆中一条弦把圆周分成1︰5两部分,则这条弦所对的圆周角为多少度
A
B
C
D
E
若∠D=1200，则∠CBE是多少度？
例1： 已知，如图，四边形ABCD的四个顶点都在⊙O上。
求证：∠B+∠D=1800
O
课堂总结：
这节课我们都有什么收获？
1、圆周角的定义：
2、圆周角定理：
顶点在圆上，两边都与圆相交的角。
一条弧所对的圆周角等于它所对的圆心角的一半。
3、圆周角定理的推论：
半圆（或直径）所对的圆周角是直角；900的圆周角所对的弦是直径。