一元一次不等式全章复习课

(共24张PPT)
《一元一次不等式》复习
60
③
判断下列代数式哪些是不等式＿＿＿＿＿＿＿
哪些是一元一次不等式＿＿＿＿＿＿
⑥
⑧
①1>－3
②
④ 4+x
⑦
⑤
问题1解⑥号不等式 把解在数轴表示出来，
并求它的：
问题2：归纳出解（6）不等式的具体步骤及每步的依据？
正整数解
最大负整数解
①②③⑥⑦⑧
③⑥⑧
问题3：取③ ⑧ 再加⑨ x<4 ⑩ x>1
从中任取两个组合成不同的不等式组，并求它的解集（利用数轴或口诀）
含有不等号的数学式子叫不等式
含有一个未知数，不等号两边都为整式，且未知数次数为1次的不等式
叫一元一次不等式。
大大取大，小小取小，大小小大取中间，
大大小小则无解，如果有等号，等号跟着走 。
问题4：取⑥号
组成不等式组，求它的解集
2、根据实际问题列出不等量关系
P≤11
y2＋1＞0
a≥3
（1）在汽车行驶的公路上,我们会看到不同的交通标志,它们有着不同的意义,如图所示,如果汽车的速度为V(km/h),你会用不等式表示图中标志的意义吗？
60
v≤60
（2）
若用t表示今天（11月23日）的气温，则t的取值范围是
.
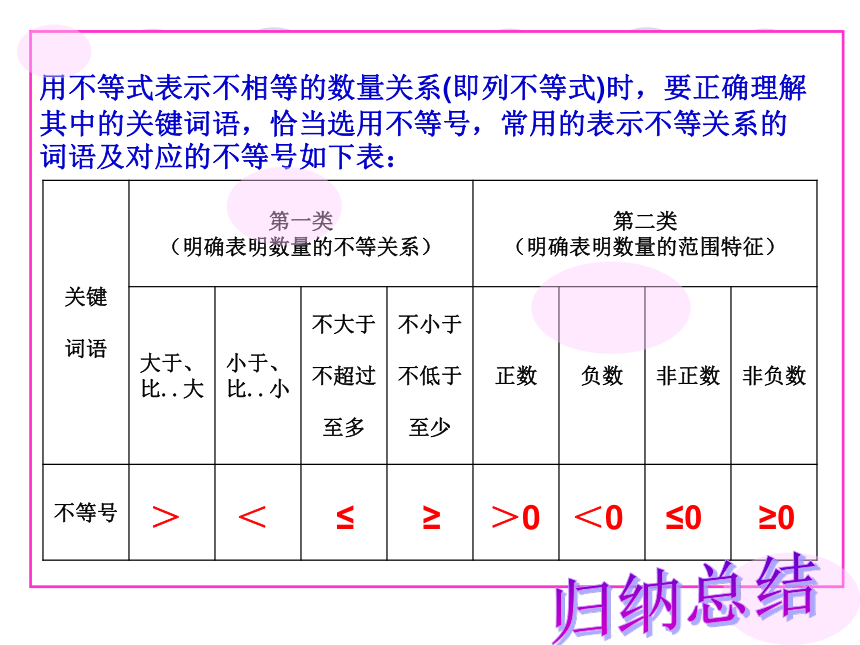
关键
词语 第一类
（明确表明数量的不等关系） 第二类
（明确表明数量的范围特征）
大于、
比..大 小于、
比..小 不大于
不超过
至多 不小于
不低于
至少 正数 负数 非正数 非负数
不等号
用不等式表示不相等的数量关系(即列不等式)时，要正确理解其中的关键词语，恰当选用不等号，常用的表示不等关系的词语及对应的不等号如下表：
＞
＜
≤
≥
＞0
＜0
≤0
≥0
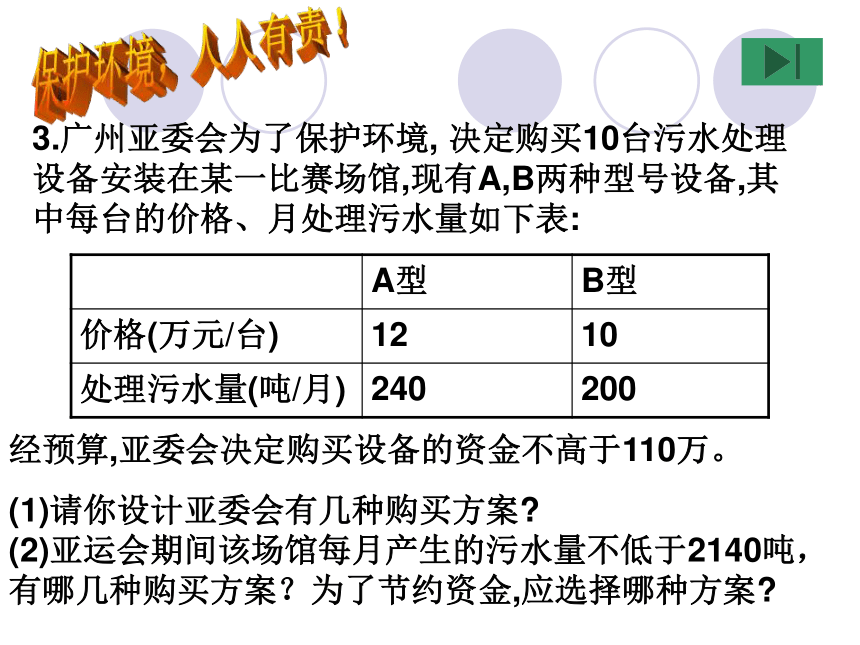
3.广州亚委会为了保护环境, 决定购买10台污水处理设备安装在某一比赛场馆,现有A,B两种型号设备,其中每台的价格、月处理污水量如下表:
A型 B型
价格(万元/台) 12 10
处理污水量(吨/月) 240 200
经预算,亚委会决定购买设备的资金不高于110万。
(1)请你设计亚委会有几种购买方案
(2)亚运会期间该场馆每月产生的污水量不低于2140吨，有哪几种购买方案？为了节约资金,应选择哪种方案
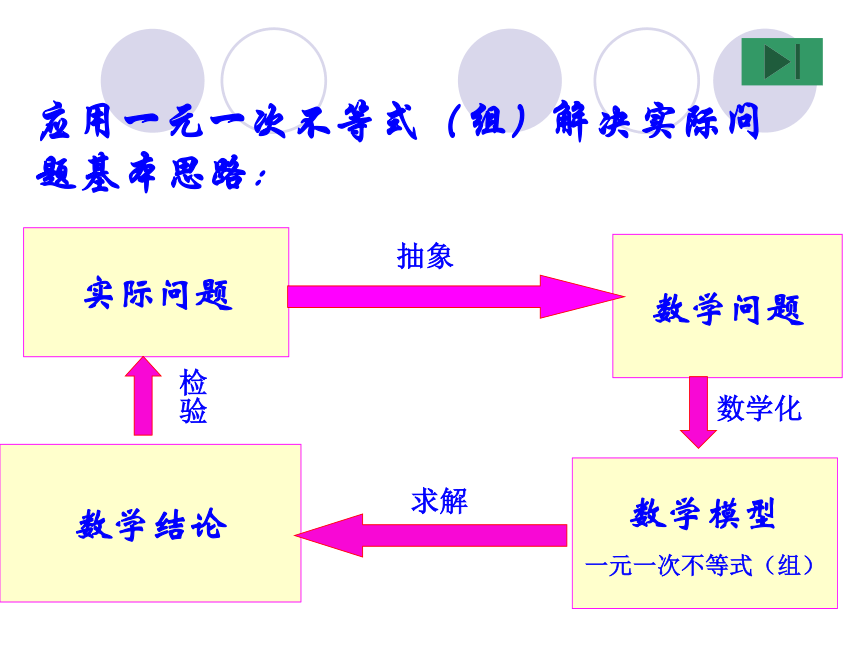
应用一元一次不等式（组）解决实际问题基本思路：
实际问题
数学问题
数学模型
一元一次不等式（组）
数学结论
抽象
求解
数学化
检验
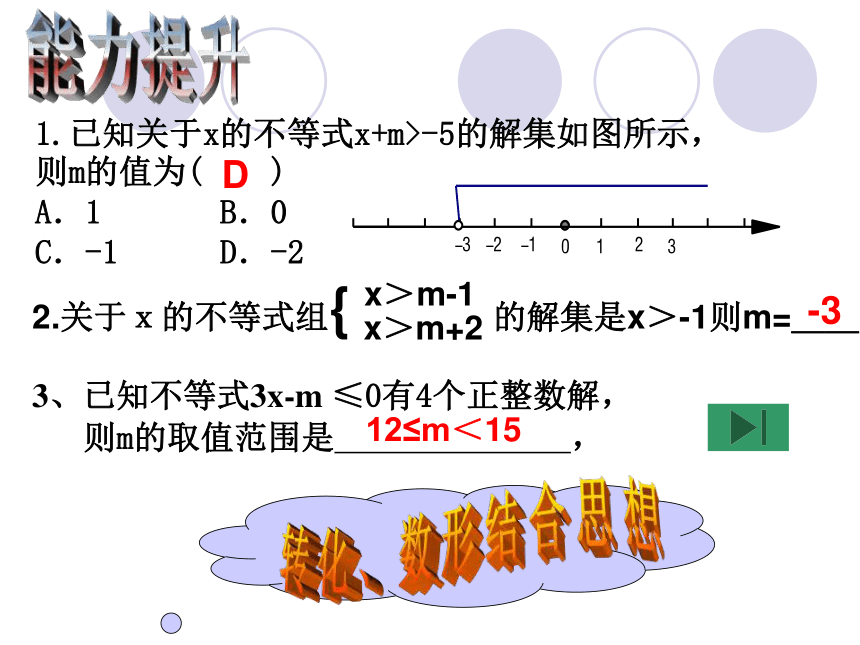
1.已知关于x的不等式x+m>-5的解集如图所示，
则m的值为( )
A．1 B．0
C．-1 D．-2
3、已知不等式3x-m ≤0有4个正整数解，
则m的取值范围是 ，
2.关于ｘ的不等式组{ 的解集是x＞-1则m=＿＿
x＞m-1
x＞m+2
D
-3
12≤m＜15
4．为了抓住广州亚运会商机，某商店决定购进A、B两种亚运会纪念品．若购进A种纪念品10件，B种纪念品5件，需要1000元；若购进A种纪念品5件，B种纪念品3件，需要550元．
（1）求购进A、B两种纪念品每件各需多少元？
（2）若该商店决定拿出1万元全部用来购进这两种纪念品，考虑市场需求，要求购进A种纪念品的数量不少于B种纪念品数量的6倍，且不超过B种纪念品数量的8倍，那么该商店共有几种进货方案？
（3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？
A 50元 B100元
5.在广州亚运会期间，某旅行社组织了一个“看亚运游广州活动”旅行团，共有253名老人报名参加．旅行前，旅行社承诺每车保证有一名随团医生，并为此次旅行请了7名医生．现打算选租甲、乙两种客车，其中甲种客车每辆载客40人，乙种客车载每辆载客30人．
(1)请帮助旅行社设计租车方案．
(2)若甲种客车租金为350元/辆，乙种客车租金为280元/辆，旅行社按哪种方案租车最省钱？此时租金是多少？
(3)旅行社在充分考虑团内老人的年龄结构特点后，为更好的照顾游客，决定同时租45座和30座的大小两种客车，大客车上至少配两名随团医生，小客车上至少配一名随团医生，为此旅行社又请了4名医生．出发时，旅行社先安排游客坐满大客车，再依次坐满小客车，最后一辆小客车即使坐不满也至少要有20座上座率．请直接写出旅行社的租车方案．
方案（1）45座4辆，30座3辆 （2）45座2辆30座6辆
6. A市和B市分别有库存污水处理设备12台和6台，现决定支援广州市10台、深圳市8台。已知从A市调运1台污水处理设备到广州市、深圳市的运费分别是400元和800元；从B市调运1台污水处理设备到广州市、深圳市的运费分别是300元和500元。若要求总运费不超过9000元，问共有几种调运方案？并求出总运费最低的调运方案，最低运费是多少？
（有三种调运方案：其中运费最低调运方案：从B市调6台机器到深圳市，从A市分别调10台、2台机器到广州市、深圳市. 最低运费为8600元）
1、求使不等式3(x-3)-1<2x成立的正整数解。
2、若不等式（a-2)x>a-2的解集为x<1，求a的取值范围( )。
A a < -2 B a < 2 C a >-2 D a >2
变式：已知不等式（a-2)x>3的解集为x< -1，则a的值是 。
B
－1
3.如果关于x的方程3x+a＝x+4的解是个非负数，则a的取值范围________
a≤4
3.学校举办“环保知识” 竞赛，设一、二、三等奖共30名，用于购买奖品的总费用， 其中奖品单价及发放方案如下表：
奖项 一等奖
二等奖 三等奖
奖品 钢笔1支
文具盒1个 迷你便签本
单价（元） 50 30 18
若本次活动设一等奖5名，则二等奖可设多少名？
不超过800元，但又不少于750元
计时制：3元/小时.
包月制：60元/月，另加1元/小时.
什么情况下采用计时制合算，什么情况下采用包月制合算呢？你能用一元一次不等式解决这个问题吗
解：设每月上网x小时。
3x< 60+x
解得 x<30
答： 若每月上网时间不足30小时则应该采用计时制，
若超过30小时则应采用包月制，
若等于30小时则两种收费制都可以.
计时制：3元/小时.
包月制：60元/月，另加1元/小时.
假设采用计时制合算.得：
假设采用包月制合算.得：
3x >60+x
解得 x>30
王海贷款5万元去做生意，贷款月利息10‰ .他决定在半年内利用赚来的钱一次性还清贷款的本息。问王海平均每个月至少要赚多少钱？（精确到元）
月利息=本金×利率
本息=本金+利息
解:设王海平均每月要赚x元钱。根据题意得
6x≥50000+50000×10‰×6
解得
答：王海平均每个月至少要赚8834元钱。
根据题意得取x=8834
某商品的零售价是每件50元，进价是每件35元。经核算，每天商店的各种费用（包括房租、售货员工资等）是120元，还需把商品售出价的10%上缴税款，问商店每天需要出售多少件这样的商品，才能保证商店每天获纯利润在100元以上（不包括100元）？
解:设商店每天出售该商品x件。根据题意得
（50-35-50×10%)x-120>100
解得
答：商店每天需要出售23件或23件以上这样的商品，才能保证商店每天获纯利润在100元以上（不包括100元）？
即 10x>220
x>22
1、当 x________时，代数式
的值是非正数。
≥
探索与思考
2、如果方程2x-1=1的解是不等式
的一个解，则 a 的取值范围是_______
a<-1
3、如果关于x的方程:3（ｘ－4）＝2ａ＋ｘ－18的解是个负数，若ａ是正整数，试确定ｘ的值。
请你来说说,你是怎样来理解不等式的
在下列数学表达式中找出不等式 :
一元一次不等式又如何理解
√
√
不等式的解集又如何理解
不等号的两边都是整式,而且只含有一个未知数,未知数的最高次数是一次,这样的不等式叫做一元一次不等式.
使不等式成立的未知数的值的全体叫不等式的解集
解不等式的依据是什么
练习:用不等号连接:
<
<
<
<
>
<
4.已知2x+y=0,且x+y+3>0.则x的取值范围_________
x＜3
1、解一元一次不等式,并把解在数轴上表示出来:
2、求使不等式3(x-3)-1<2x成立的正整数解。
挑战自我
3、若不等式（a-2)x>a-2的解集为x<1，求a的取值范围( )。
A a < -2 B a < 2 C a >-2 D a >2
变式：已知不等式（a-2)x>3的解集为x< -1，则a的值是 。
B
－1
这节课我们复习了哪些知识
你有什么收获
还有哪些疑惑