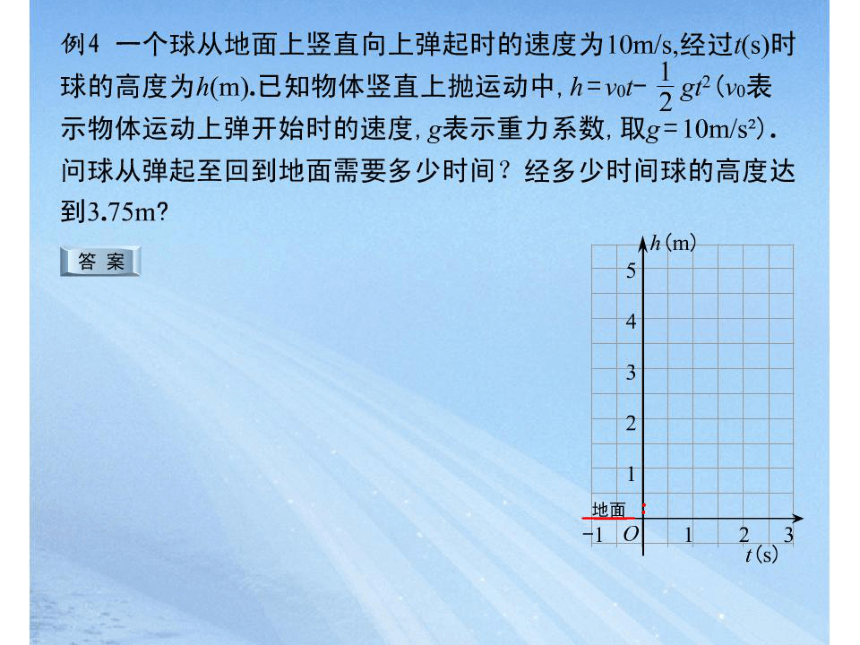
2.4二次函数的应用(3)

(共16张PPT)
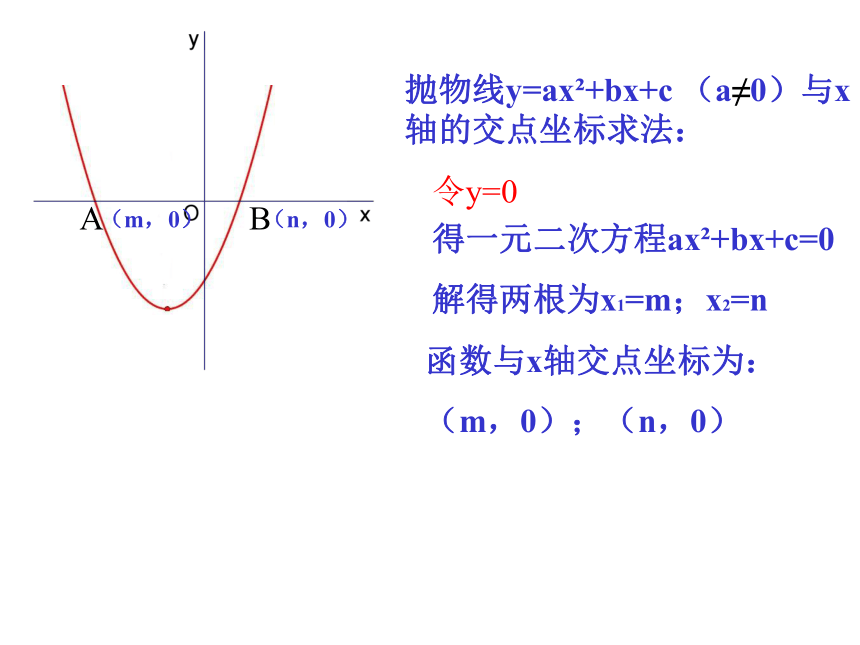
A
B
抛物线y=ax +bx+c （a≠0）与x轴的交点坐标求法：
令y=0
得一元二次方程ax +bx+c=0
解得两根为x1=m；x2=n
函数与x轴交点坐标为：
（m，0）；（n，0）
（m，0）
（n，0）
练习：求出下列二次函数和X轴的交点坐标：
y=x -2x+1 2. y=2x -4x+8
3. y=x -4x-8 4. y=3（x-4)（x+3)
1.y=X -4x+4
2.y=2X -x-1
3.y=3X -4x+6
看谁快
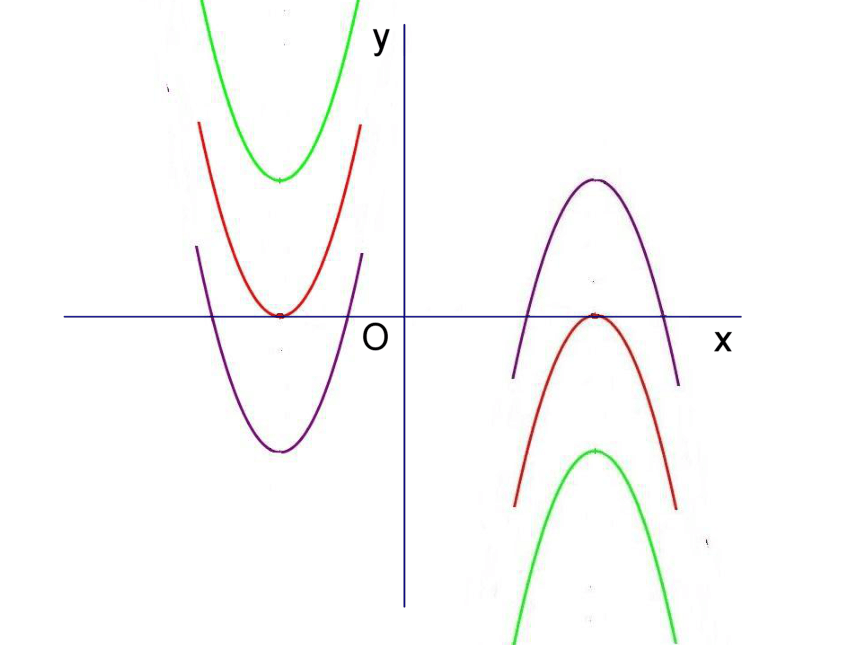
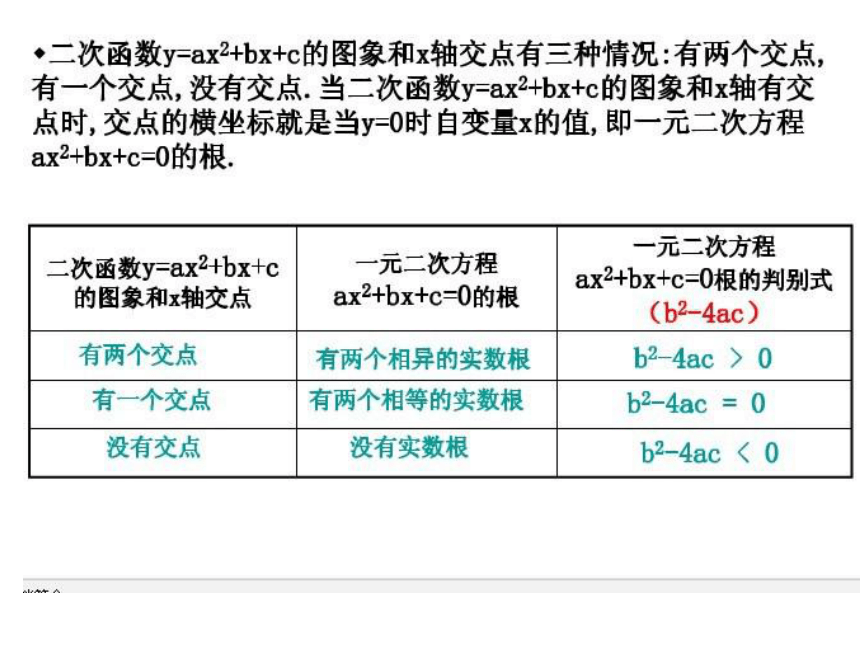
不用画图,试判断下列抛物线同x轴交点情况:
4.y=-9X -4x+3
一个交点
两个交点
没有交点
两个交点
b2-4ac的符号
二次函数y=ax +bx+c
归纳小结：
y=0
一元二次方程ax +bx+c=0
两根为x1=m；x2=n
函数与x轴交点坐标为：
（m，0）；（n，0）
反过来，也可利用二次函数的图象
求一元二次方程的解。
二次函数y=ax +bx+c
归纳小结：
y=0
一元二次方程ax +bx+c=0
两根为x1=m；x2=n
函数与x轴交点坐标为：
（m，0）；（n，0）
在本节的例5中，我们把一元二次方程X +X－1= 0 的解看做是抛物线y=x +x-1与x轴交点的横坐标，利用图象求出了方程的近似解。如果把方程x +x-1 = 0变形成 x = -x+1，那么方程的解也可以看成怎样的两个函数的交点的横坐标？用不同图象解法试一试，结果相同吗？在不使用计算机画图象的情况下，你认为哪一种方法较为方便？
探究活动：
1、通过这节课的学习活动你有哪些收获？
2、对这节课的学习，你还有什么想法吗？