1.1 认识三角形 课时达标检测(含解析)
文档属性
| 名称 | 1.1 认识三角形 课时达标检测(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 21:31:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2021年八年级上册数学同步练习卷
1.1 认识三角形
一、单选题
1.三角形一个外角小于与它相邻的内角,这个三角形( )
A.是钝角三角形 B.是锐角三角形 C.是直角三角形 D.属于哪一类不能确定.
2.已知,则为( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都有可能
3. 叫做三角形
A.连接任意三点组成的图形
B.由不在同一条直线上的三条线段首尾顺次相接所成的图形
C.由三条线段组成的图形
D.以上说法均不对
4.下列长度的三条线段能组成三角形的是( )
A.3,3,4 B.7,4,2 C.3,4,8 D.2,3,5
5.一幅三角板,如图所示叠放在一起,则图中∠的度数是( )
A.75° B.60° C.65° D.55°
6.在中,,与的平分线交于点,则的度数为( )
A. B. C. D.
7.如图,已知中,,若沿图中虚线剪去,则等于( )
A.90° B.135° C.270° D.315°
8.若a、b、c为三角形的三条边,则+|b-a-c|=( ).
A.2b-2c B.2a C.2 D.2a-2c
9.如图,D,E分别是的边AC,BC的中点,则下列说法错误的是( )
A.DE是的中线 B.BD是的中线
C. D.BD是的角平分线
10.如图,直线EF直线GH,Rt△ABC中,∠C=90°,顶点A在GH上,顶点B在EF上,且BA平分∠DBE,若∠CAD=26°,则∠BAD的度数为( )
A.26° B.32° C.34° D.45°
11.如图,,M,N分别是边上的定点,P,Q分别是边上的动点,记,当的值最小时,关于,的数量关系正确的是( )
A. B. C. D.
12.如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )
A.120° B.135° C.150° D.不能确定
二、填空题
13.如图,图中以BC为边的三角形的个数为_____.
14.一个多边形的内角和是1800°,这个多边形是_____边形.
15.若直角三角形的两个锐角的比是2:7,则这个直角三角形的较大的锐角是___________度.
16.如图,在△ABC中,E,D,F分别是AD,BF,CE的中点若△DEF的面积是1cm?,则S△ABC=_______.
17.若△ABC三条边长为a,b,c,化简:|a-b-c|-|a+c-b|=__________.
18.如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
三、解答题
19.在△ABC中,AB=9,AC=2,并且BC的长为偶数,求△ABC的周长.
20.如图,在中,点D在AC上,点P在BD上,求证:.
21.如图,在ABC中,AB=AC,AC边上的中线BD把ABC的周长分成12cm和15cm两部分,求ABC各边的长.
22.(1)如图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系: ;
(2)如图2,∠1+∠2+∠3+∠4+∠5+∠6+∠7= 度;
(3)如图3所示,已知∠1=∠2,∠3=∠4,猜想∠B,∠P,∠D之间的数量关系,并证明.
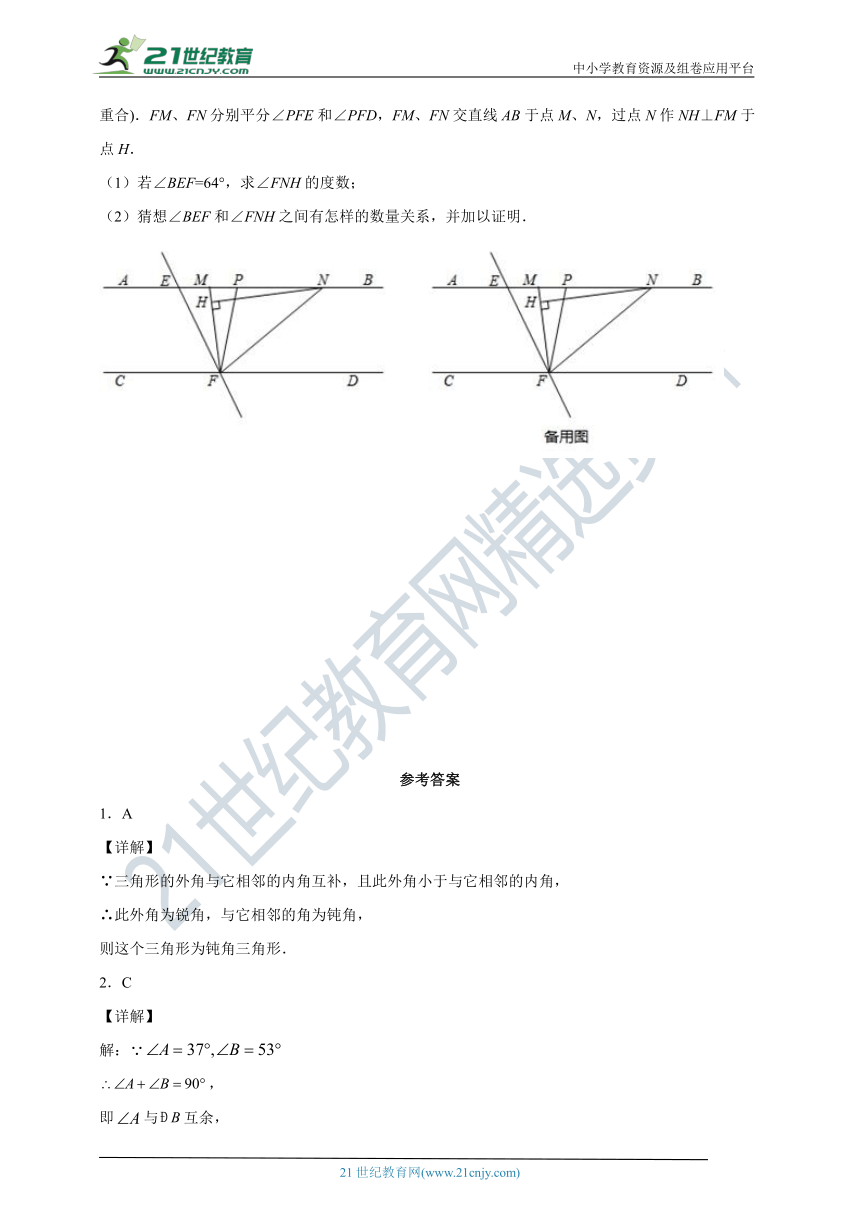
23.如图,已知,直线EF与AB、CD分别交于点E、F,点P是射线EB上一点(与点E不重合).FM、FN分别平分∠PFE和∠PFD,FM、FN交直线AB于点M、N,过点N作NH⊥FM于点H.
(1)若∠BEF=64°,求∠FNH的度数;
(2)猜想∠BEF和∠FNH之间有怎样的数量关系,并加以证明.
参考答案
1.A
【详解】
∵三角形的外角与它相邻的内角互补,且此外角小于与它相邻的内角,
∴此外角为锐角,与它相邻的角为钝角,
则这个三角形为钝角三角形.
2.C
【详解】
解:
,
即与互余,
则为直角三角形,
3.B
【详解】
因为三角形的定义是:由不在同一条直线上的三条线段首尾顺次相接所成的图形.
4.A
【详解】
解:A、3+3>4,能构成三角形,故此选项正确;
B、4+2<7,不能构成三角形,故此选项错误;
C、3+4<8,不能构成三角形,故此选项错误;
D、2+3=5,不能构成三角形,故此选项错误.
5.A
【详解】
根据题意有,
,
,
6.C
【详解】
解:
,
和的平分线交于点P,
,
7.C
【详解】
如图,由三角形的外角性质得:,
,
,
8.B
【详解】
根据三角形的三边关系可知,
∴
∴
9.D
【详解】
点D,E分别是的边AC,BC的中点,
,
是的边AC上的中线,DE是的边BC上的中线,
则选项A、B、C正确,
因为BD不一定平分,
所以选项D错误,
10.B
【详解】
∵∠C=90°,∠CAD=26°
∴∠ADC=90°-26°=64°
∵EF∥GH,
∴∠BAH=∠ABE,∠ADC=∠EBC=64°
∵BA平分∠DBE,
∴∠ABC=∠ABE=64°×=32°,
∴∠BAD=∠ABC=∠ABE=32°
11.B
【详解】
如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则此时的值最小.
易知,.
∵,,
∴.
12.B
【详解】
解:
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°-90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°-90°=45°,
∴∠F=180°-(∠FAD+∠FDA)=180-45°=135°.
13.4.
【详解】
解:∵以BC为公共边的三角形有△BCD,△BCE,△BCF,△ABC,
∴以BC为公共边的三角形的个数是4个.
14.十二.
【详解】
设这个多边形是n边形,
根据题意得:(n-2)×180°=1800°,
解得:n=12.
∴这个多边形是十二边形.
15.70
【详解】
∵直角三角形中的两个锐角互余,
∴较大的锐角=90°÷(2+7)×7=70°.
16.7
【详解】
连接AF,
∵E是AD的中点,
∴
∴,
∵点D是BF的中点,
∴,
∵点F是CE的中点,
∴,
同理可得:,
∴=1+2+2+2=7,
故答案为:7.
17.2b-2a
【详解】
根据三角形的三边关系得:a﹣b﹣c<0,c+a﹣b>0,
∴原式=﹣(a﹣b﹣c)﹣(a+c﹣b)=﹣a+b+c﹣a﹣c+b=2b﹣2a.
18.50°
【详解】
解:如图,设∠DAB=∠BAC=x,即∠1=∠2=x.∵EF∥GH,∴∠2=∠3.在△ABC内,∠4=180°﹣∠ACB﹣∠1﹣∠3=180°﹣∠ACB﹣2x=80°﹣2x.∵直线BD平分∠FBC,∴∠5=(180°﹣∠4)=(180°﹣80°+2x)=50°+x,∴∠DBA=180°﹣∠3﹣∠4﹣∠5
=180°﹣x﹣(80°﹣2x)﹣(50°+x)
=180°﹣x﹣80°+2x﹣50°﹣x
=50°.
故答案为50°.
19.21
【详解】
根据三角形的三边关系得:
9﹣2<BC<9+2,
即7<BC<11,
∵BC为偶数,
∴AC=8或10,
∴△ABC的周长为:9+2+8=19或9+2+10=21
20.见解析
【详解】
∵在中,,
在中,,
.
,
.
21.AB=AC=8cm,BC=11cm或AB=AC=10cm,BC=7cm
解答.
【详解】
解:设AB=xcm,BC=ycm.
则有以下两种情况:
(1)当AB+AD=12cm,BC+CD=15cm时,,解得 ,即AB=AC=8cm,BC=11cm,符合三边关系;
(2)当AB+AD=15cm,BC+CD=12cm时,,解得 ,即AB=AC=10cm,BC=7cm,符合三边关系.
22.(1)∠A+∠B=∠C+∠D;(2)540°;(3)2∠P=∠D+∠B.
【详解】
解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠B=∠C+∠D,
故答案为:∠A+∠B=∠C+∠D;
(2)如图,
∵∠6,∠7的和与∠8,∠9的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=540°;
(3)∠DAP+∠D=∠P+∠DCP,
①∠PCB+∠B=∠PAB+∠P,
②∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B.
23.(1)32°;(2),理由见解析
【详解】
解:(1),
,
,
,
、分别平分和,
,,
,
,
,
;
(2),
证明:设,
,
,
,
,
、分别平分和,
,,
,
,
,
,
即.
_21?????????è?????(www.21cnjy.com)_
浙教版2021年八年级上册数学同步练习卷
1.1 认识三角形
一、单选题
1.三角形一个外角小于与它相邻的内角,这个三角形( )
A.是钝角三角形 B.是锐角三角形 C.是直角三角形 D.属于哪一类不能确定.
2.已知,则为( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都有可能
3. 叫做三角形
A.连接任意三点组成的图形
B.由不在同一条直线上的三条线段首尾顺次相接所成的图形
C.由三条线段组成的图形
D.以上说法均不对
4.下列长度的三条线段能组成三角形的是( )
A.3,3,4 B.7,4,2 C.3,4,8 D.2,3,5
5.一幅三角板,如图所示叠放在一起,则图中∠的度数是( )
A.75° B.60° C.65° D.55°
6.在中,,与的平分线交于点,则的度数为( )
A. B. C. D.
7.如图,已知中,,若沿图中虚线剪去,则等于( )
A.90° B.135° C.270° D.315°
8.若a、b、c为三角形的三条边,则+|b-a-c|=( ).
A.2b-2c B.2a C.2 D.2a-2c
9.如图,D,E分别是的边AC,BC的中点,则下列说法错误的是( )
A.DE是的中线 B.BD是的中线
C. D.BD是的角平分线
10.如图,直线EF直线GH,Rt△ABC中,∠C=90°,顶点A在GH上,顶点B在EF上,且BA平分∠DBE,若∠CAD=26°,则∠BAD的度数为( )
A.26° B.32° C.34° D.45°
11.如图,,M,N分别是边上的定点,P,Q分别是边上的动点,记,当的值最小时,关于,的数量关系正确的是( )
A. B. C. D.
12.如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )
A.120° B.135° C.150° D.不能确定
二、填空题
13.如图,图中以BC为边的三角形的个数为_____.
14.一个多边形的内角和是1800°,这个多边形是_____边形.
15.若直角三角形的两个锐角的比是2:7,则这个直角三角形的较大的锐角是___________度.
16.如图,在△ABC中,E,D,F分别是AD,BF,CE的中点若△DEF的面积是1cm?,则S△ABC=_______.
17.若△ABC三条边长为a,b,c,化简:|a-b-c|-|a+c-b|=__________.
18.如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
三、解答题
19.在△ABC中,AB=9,AC=2,并且BC的长为偶数,求△ABC的周长.
20.如图,在中,点D在AC上,点P在BD上,求证:.
21.如图,在ABC中,AB=AC,AC边上的中线BD把ABC的周长分成12cm和15cm两部分,求ABC各边的长.
22.(1)如图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系: ;
(2)如图2,∠1+∠2+∠3+∠4+∠5+∠6+∠7= 度;
(3)如图3所示,已知∠1=∠2,∠3=∠4,猜想∠B,∠P,∠D之间的数量关系,并证明.
23.如图,已知,直线EF与AB、CD分别交于点E、F,点P是射线EB上一点(与点E不重合).FM、FN分别平分∠PFE和∠PFD,FM、FN交直线AB于点M、N,过点N作NH⊥FM于点H.
(1)若∠BEF=64°,求∠FNH的度数;
(2)猜想∠BEF和∠FNH之间有怎样的数量关系,并加以证明.
参考答案
1.A
【详解】
∵三角形的外角与它相邻的内角互补,且此外角小于与它相邻的内角,
∴此外角为锐角,与它相邻的角为钝角,
则这个三角形为钝角三角形.
2.C
【详解】
解:
,
即与互余,
则为直角三角形,
3.B
【详解】
因为三角形的定义是:由不在同一条直线上的三条线段首尾顺次相接所成的图形.
4.A
【详解】
解:A、3+3>4,能构成三角形,故此选项正确;
B、4+2<7,不能构成三角形,故此选项错误;
C、3+4<8,不能构成三角形,故此选项错误;
D、2+3=5,不能构成三角形,故此选项错误.
5.A
【详解】
根据题意有,
,
,
6.C
【详解】
解:
,
和的平分线交于点P,
,
7.C
【详解】
如图,由三角形的外角性质得:,
,
,
8.B
【详解】
根据三角形的三边关系可知,
∴
∴
9.D
【详解】
点D,E分别是的边AC,BC的中点,
,
是的边AC上的中线,DE是的边BC上的中线,
则选项A、B、C正确,
因为BD不一定平分,
所以选项D错误,
10.B
【详解】
∵∠C=90°,∠CAD=26°
∴∠ADC=90°-26°=64°
∵EF∥GH,
∴∠BAH=∠ABE,∠ADC=∠EBC=64°
∵BA平分∠DBE,
∴∠ABC=∠ABE=64°×=32°,
∴∠BAD=∠ABC=∠ABE=32°
11.B
【详解】
如图,作M关于的对称点,N关于的对称点,连接交于Q,交于P,则此时的值最小.
易知,.
∵,,
∴.
12.B
【详解】
解:
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°-90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°-90°=45°,
∴∠F=180°-(∠FAD+∠FDA)=180-45°=135°.
13.4.
【详解】
解:∵以BC为公共边的三角形有△BCD,△BCE,△BCF,△ABC,
∴以BC为公共边的三角形的个数是4个.
14.十二.
【详解】
设这个多边形是n边形,
根据题意得:(n-2)×180°=1800°,
解得:n=12.
∴这个多边形是十二边形.
15.70
【详解】
∵直角三角形中的两个锐角互余,
∴较大的锐角=90°÷(2+7)×7=70°.
16.7
【详解】
连接AF,
∵E是AD的中点,
∴
∴,
∵点D是BF的中点,
∴,
∵点F是CE的中点,
∴,
同理可得:,
∴=1+2+2+2=7,
故答案为:7.
17.2b-2a
【详解】
根据三角形的三边关系得:a﹣b﹣c<0,c+a﹣b>0,
∴原式=﹣(a﹣b﹣c)﹣(a+c﹣b)=﹣a+b+c﹣a﹣c+b=2b﹣2a.
18.50°
【详解】
解:如图,设∠DAB=∠BAC=x,即∠1=∠2=x.∵EF∥GH,∴∠2=∠3.在△ABC内,∠4=180°﹣∠ACB﹣∠1﹣∠3=180°﹣∠ACB﹣2x=80°﹣2x.∵直线BD平分∠FBC,∴∠5=(180°﹣∠4)=(180°﹣80°+2x)=50°+x,∴∠DBA=180°﹣∠3﹣∠4﹣∠5
=180°﹣x﹣(80°﹣2x)﹣(50°+x)
=180°﹣x﹣80°+2x﹣50°﹣x
=50°.
故答案为50°.
19.21
【详解】
根据三角形的三边关系得:
9﹣2<BC<9+2,
即7<BC<11,
∵BC为偶数,
∴AC=8或10,
∴△ABC的周长为:9+2+8=19或9+2+10=21
20.见解析
【详解】
∵在中,,
在中,,
.
,
.
21.AB=AC=8cm,BC=11cm或AB=AC=10cm,BC=7cm
解答.
【详解】
解:设AB=xcm,BC=ycm.
则有以下两种情况:
(1)当AB+AD=12cm,BC+CD=15cm时,,解得 ,即AB=AC=8cm,BC=11cm,符合三边关系;
(2)当AB+AD=15cm,BC+CD=12cm时,,解得 ,即AB=AC=10cm,BC=7cm,符合三边关系.
22.(1)∠A+∠B=∠C+∠D;(2)540°;(3)2∠P=∠D+∠B.
【详解】
解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠B=∠C+∠D,
故答案为:∠A+∠B=∠C+∠D;
(2)如图,
∵∠6,∠7的和与∠8,∠9的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=540°;
(3)∠DAP+∠D=∠P+∠DCP,
①∠PCB+∠B=∠PAB+∠P,
②∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B.
23.(1)32°;(2),理由见解析
【详解】
解:(1),
,
,
,
、分别平分和,
,,
,
,
,
;
(2),
证明:设,
,
,
,
,
、分别平分和,
,,
,
,
,
,
即.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
