第1章 三角形的初步知识课时达标检测题(含解析)
文档属性
| 名称 | 第1章 三角形的初步知识课时达标检测题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2021年八年级上册数学同步练习卷
第1章 本章复习与测试
一、单选题(共30分)
1.(本题3分)下列语句是命题的是( )
A.作直线AB的垂线 B.在线段AB上取点C
C.同旁内角互补 D.垂线段最短吗?
2.(本题3分)命题“垂直于同一条直线的两条直线互相平行”的条件是( )
A.垂直 B.两条直线 C.同一条直线 D.两条直线垂直于同一条直线
3.(本题3分)如果两个直角三角形的两条直角边对应相等,那么这两个直角三角形全等的依据是( )
A.SSS B.AAS C.SAS D.HL
4.(本题3分)下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4 B.5,7,7 C.5,6,12 D.6,8,10
5.(本题3分)如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )
A.50 B.62 C.65 D.68
6.(本题3分)如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C.下列结论错误的是( )
A.AD=CP B.△ABP≌△CBP C.△ABD≌△CBD D.∠ADB=∠CDB.
7.(本题3分)下列条件中,不能判定两个直角三角形全等的是( )
A.两条直角边对应相等 B.有两条边对应相等
C.斜边和一锐角对应相等 D.一条直角边和斜边对应相等
8.(本题3分)将一副三角板按如图放置,则下列结论①;②如果则有AC∥DE;③如果,则有BC∥AD;④如果,必有.其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
9.(本题3分)如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是( )
A.5cm B.6cm C.7cm D.8cm
10.(本题3分)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
二、填空题(共21分)
11.(本题3分)如图所示,AD=BC,AC=BD,用三角形全等的判定“边边边”可证明________≌ _______或________≌________.
12.(本题3分)中,,,则BC边上的中线的范围为______ .
13.(本题3分)如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,你所添加的条件是________(只添一个即可).
14.(本题3分)如图,AB,CD,EF相交于点O,且它们均被点O平分,则图中共有____对全等三角形.
15.(本题3分)如图,在△ABC中,∠B=∠C,BD=CE,BE=CF.若∠A=40°,则∠DEF的度数为____.
16.(本题3分)如图,在△ABC和△ADC中,下列论断:①AB=AD;②∠ABC=∠ADC=90°;③BC=DC.把其中两个论断作为条件,另一个论断作为结论,可以写出_个真命题.
17.(本题3分)如图,AD=CB,若利用“边边边”来判定△ABC≌△CDA,则需添加一个直接条件是__;若利用“边角边”来判定△ABC≌△CDA,则需添加一个直接条件是__.
三、解答题(共49分)
18.(本题7分)已知:如图,是的中点,,.
求证:.
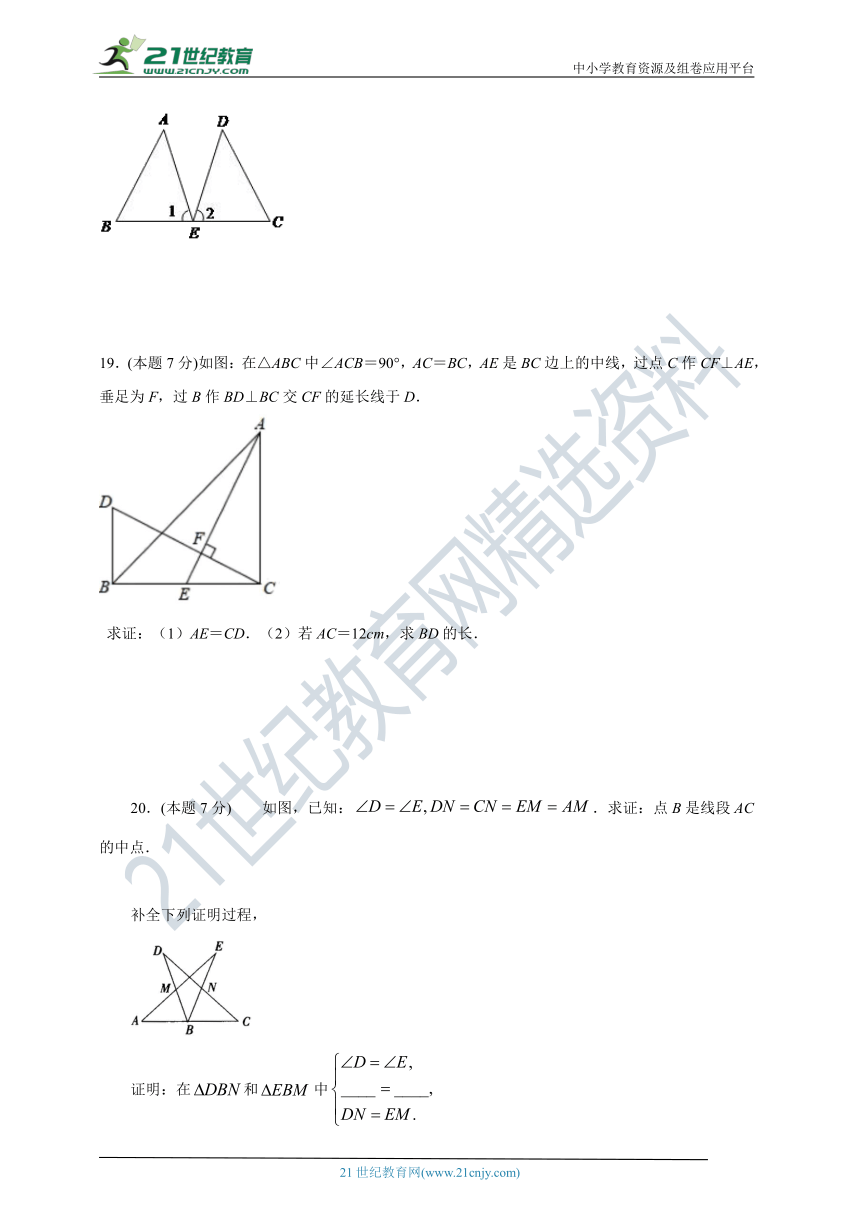
19.(本题7分)如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE, 垂足为F,过B作BD⊥BC交CF的延长线于D.
求证:(1)AE=CD.(2)若AC=12cm,求BD的长.
20.(本题7分) 如图,已知:.求证:点B是线段AC的中点.
补全下列证明过程,
证明:在和中
∴≌(______)
∴______=______.
在和中
∴≌(根据______) ∴
即点B是线段AC的中点.
21.(本题7分)如图,已知D为△ABC的BC边的中点,DE、DF分别平分∠ADB和∠ADC,
求证:BE+CF>EF.
22.(本题7分)为进一步打造“宜居重庆”,某区拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请在答题卷的原图上利用尺规作图作出音乐喷泉M的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
23.(本题7分)如图,已知,.
求证:;
若,问经过怎样的变换能与重合?
24.(本题7分)如图,在长方形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连结DE,动点P从点B出发,以每秒2个单位的速度沿BC→CD→DA向终点A运动,设点P的运动时间为t(s),当t为何值时,△ABP和△DCE全等?
参考答案
1.C
【详解】
A. 作直线AB的垂线为描叙性语言,不是命题,故错误;
B. 在线段AB上取点C为描叙性语言,不是命题,故错误;
C. 同旁内角互补为命题,故正确;
D. 垂线段最短吗为疑问句,不是命题,故错误.
2.D
【详解】
解:命题“垂直于同一条直线的两条直线互相平行”的条件是两条直线垂直于同一条直线,
3.C
【解析】解:两边及夹角对应相等的两个三角形全等,这为“边角边”定理,简写成“SAS”.故选C.
4.C
【详解】
A.∵2+3>4,∴能组成三角形,故A错误;
B.∵5+7>7,∴不能组成三角形,故B错误;
C.∵5+6<12,∴不能组成三角形,故C正确;
D.∵6+8>10,∴能组成三角形,故D错误;
5.A
【详解】
∵如图,AE⊥AB且AE=AB,EF⊥FH,BG⊥FH?∠EAB=∠EFA=∠BGA=90?,∠EAF+∠BAG=90?,∠ABG+∠BAG=90??∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG?△EFA≌△AGB,
∴AF=BG,AG=EF.
同理证得△BGC≌△CHD得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16
故S= (6+4)×16?3×4?6×3=50.
故选A.
6.A
【详解】
∵点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C.
∴PA=PC,
∴△ABP≌△CBP ,△ABD≌△CBD ,
∴∠ADB=∠CDB,
故选A.
7.B
【解析】
根据全等三角形的判定SAS,可知两条直角边对应相等的两个直角三角形全等,故A不正确;
根据一条直角边和斜边对应相等的两个直角三角形,符合全等三角形的判定定理HL,能判定全等;若两条直角边对应相等的两个直角三角形,符合全等三角形的判定定理SAS,也能判全等,但是有两边对应相等,没说明是什么边对应,故不能判定,故B正确.
根据全等三角形的判定AAS,可知斜边和一锐角对应相等的两直角三角形全等,故C不正确;
根据直角三角形的判定HL,可知一条直角边和斜边对应相等两直角三角形全等,故D不正确.
故选B.
8.B
【详解】
∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,①正确;
∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴AC∥DE,②正确;
∵∠2=30°,
∴∠1+∠2+∠3=150°,
又∵∠C=45°,
∴BC与AD不平行,③错误;
∵∠2=30°,
∴AC∥DE,
∴∠4=∠C,④正确.
9.B
【详解】
∵AD是∠CAB的角平分线,DE⊥AB,∠C=90°,
∴DC=DE,AC=AE,
∴△DEB的周长=DE+BE+BD=BE+DC+BD=BE+BC=BE+AE=AB=6cm,
10.C
【详解】
试题分析:如图,过点E作EF⊥BC交BC于点F,根据角平分线的性质可得DE=EF=2,所以△BCE的面积等于,故答案选C.
考点:角平分线的性质;三角形的面积公式.
11.△ADC, △BCD , △ADB, △BCA
【解析】
试题解析:在△ADC和△BCD中;
∴△ADC≌△BCD(SSS).
在△ADB和△BCA中;
∴△ADB≌△BCA(SSS).
故答案为:△ADC,△BCD;△ADB,△BCA.
点睛:三条边对应相等,两个三角形全等.
12.1【详解】
延长AD至E,使DE=AD,连接CE,
在△ABD与△ECD中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=10,
在△ACE中,CE-AC<AE<CE+AC,AC=8,
即2<2AD<18,
1<AD<9,
13.∠BAC=∠DAC(答案不唯一)
【解析】
添加的条件是:∠ACB=∠ACD,理由:∵ ∠ACB=∠ACD,∠B=∠D,AC=AC,∴ △ABC≌△ADC;添加的条件是:∠BAC=∠DAC,理由:∵ ∠BAC=∠DAC,∠B=∠D,AC=AC;∴ △ABC≌△ADC.
14.3
【详解】
根据对顶角相等和线段的中点的定义,运用SAS可得△AOE≌△BOF,△AOC≌△BOD,△COE≌△DOF,共3对.做题时从已知开始结合全等的判定方法由易到难逐个找寻.
故答案为3.
15.70°
【详解】
由等腰三角形的性质得出∠B=∠C=70°,再根据SAS证得△BDE≌△CEF,得出∠BDE=∠CEF,运用三角形的外角性质得出∠CEF+∠DEF=∠B+∠BDE,即可得出∠DEF=∠B=70°.
16.2
【详解】
根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为2.
17.AB=CD ∠DAC=∠BCA
【解析】
∵在△ABC和△CDA中,
∴△ABC≌△CDA(SSS);
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
故答案为AB=CD,∠DAC=∠BCA.
18.证明:是的中点
,
在和中,
,
,
,
(SAS),
.
19.(1)见解析;(2)6
【详解】
证明:(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,且BC=CA,
在△DBC和△ECA中,
∴△DBC≌△ECA(AAS).
∴AE=CD;
(2) 由(1)可得△DBC≌△ECA
∴CE=BD,
∵BC=AC=12cm AE是BC的中线,
∴,
∴BD=6cm.
20.
【详解】
证明:在和中
∴≌()
∴.
在和中
∴≌(根据)
∴
即点B是线段AC的中点.
21.证明见解析.
【解析】
试题分析:在 DA 上取一点 M ,使 DM=DB=DC ,连结 EM 、 MF ,实质上是将△DBE 及△DFC 分别沿 DE 、 DF 翻折 180° 得到△DEM 及△MFD ,从而使问题得到解决的 .
试题解析:在 DA 上取一点 M ,使 DM=DB=DC ,连结 EM 、 MF ,
∵ DE 平分∠ADB ,
∴ ∠BDE= ∠EDM.
又∵ DM=BD , DE=DE ,
∴ △BED ≌△MED.
同理可得△MFD ≌△CFD.
∴ BE=EM , CF=MF.
∵ 在△EMF 中, EM+MF>EF.
∴ BE+CF>EF.
22.解:作AB的垂直平分线,以点C为圆心,以AB的一半为半径画弧交AB的垂直平分线于点M即可.
【详解】
易得M在AB的垂直平分线上,且到C的距离等于AB的一半.
23.(1)见解析;(2)先将绕点逆时针旋转,再将沿直线对折,即可得与重合.或先将绕点顺时针旋转,再将沿直线对折,即可得与重合
【分析】
(1)要证明∠B=∠C,可以证明它们所在的三角形全等,即证明△ABE≌△ACD;已知两边和它们的夹角对应相等,由SAS即可判定两三角形全等.
(2)因为△ABE≌△ACD,公共点A,对应线段CD与BE相交,所以要通过旋转,翻折两次完成.
【详解】
在与中,,,;
∴,
∴.
先将绕点逆时针旋转,
再将沿直线对折,即可得与重合.
或先将绕点顺时针旋转,
再将沿直线对折,即可得与重合.
24.当t=1或7时,△ABP和△DCE全等
【详解】
试题分析:由条件可以知道BP=2t,当点P在线段BC上时,可以知道BP=CE,当点P在线段DA上时,有AD=CE,分别可得到关于t的方程,可求得t的值.
试题解析:∵AB=CD,∠A=∠B=∠DCE=90°,
∴△ABP≌△DCE或△BAP≌△DCE.
当△ABP≌△DCE时,BP=CE=2,
此时2t=2,解得t=1.
当△BAP≌△DCE时,AP=CE=2,
此时BC+CD+DP=BC+CD+(DA-AP)=6+4+(6-2)=14,即2t=14,解得t=7.
∴当t=1或7时,△ABP和△DCE全等.
_21?????????è?????(www.21cnjy.com)_
浙教版2021年八年级上册数学同步练习卷
第1章 本章复习与测试
一、单选题(共30分)
1.(本题3分)下列语句是命题的是( )
A.作直线AB的垂线 B.在线段AB上取点C
C.同旁内角互补 D.垂线段最短吗?
2.(本题3分)命题“垂直于同一条直线的两条直线互相平行”的条件是( )
A.垂直 B.两条直线 C.同一条直线 D.两条直线垂直于同一条直线
3.(本题3分)如果两个直角三角形的两条直角边对应相等,那么这两个直角三角形全等的依据是( )
A.SSS B.AAS C.SAS D.HL
4.(本题3分)下列各组数中,不可能成为一个三角形三边长的是( )
A.2,3,4 B.5,7,7 C.5,6,12 D.6,8,10
5.(本题3分)如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按图中所标注的数据,计算图中实线所围成的面积S是( )
A.50 B.62 C.65 D.68
6.(本题3分)如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C.下列结论错误的是( )
A.AD=CP B.△ABP≌△CBP C.△ABD≌△CBD D.∠ADB=∠CDB.
7.(本题3分)下列条件中,不能判定两个直角三角形全等的是( )
A.两条直角边对应相等 B.有两条边对应相等
C.斜边和一锐角对应相等 D.一条直角边和斜边对应相等
8.(本题3分)将一副三角板按如图放置,则下列结论①;②如果则有AC∥DE;③如果,则有BC∥AD;④如果,必有.其中正确的有( )
A.①②③ B.①②④ C.③④ D.①②③④
9.(本题3分)如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是( )
A.5cm B.6cm C.7cm D.8cm
10.(本题3分)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
二、填空题(共21分)
11.(本题3分)如图所示,AD=BC,AC=BD,用三角形全等的判定“边边边”可证明________≌ _______或________≌________.
12.(本题3分)中,,,则BC边上的中线的范围为______ .
13.(本题3分)如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,你所添加的条件是________(只添一个即可).
14.(本题3分)如图,AB,CD,EF相交于点O,且它们均被点O平分,则图中共有____对全等三角形.
15.(本题3分)如图,在△ABC中,∠B=∠C,BD=CE,BE=CF.若∠A=40°,则∠DEF的度数为____.
16.(本题3分)如图,在△ABC和△ADC中,下列论断:①AB=AD;②∠ABC=∠ADC=90°;③BC=DC.把其中两个论断作为条件,另一个论断作为结论,可以写出_个真命题.
17.(本题3分)如图,AD=CB,若利用“边边边”来判定△ABC≌△CDA,则需添加一个直接条件是__;若利用“边角边”来判定△ABC≌△CDA,则需添加一个直接条件是__.
三、解答题(共49分)
18.(本题7分)已知:如图,是的中点,,.
求证:.
19.(本题7分)如图:在△ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF⊥AE, 垂足为F,过B作BD⊥BC交CF的延长线于D.
求证:(1)AE=CD.(2)若AC=12cm,求BD的长.
20.(本题7分) 如图,已知:.求证:点B是线段AC的中点.
补全下列证明过程,
证明:在和中
∴≌(______)
∴______=______.
在和中
∴≌(根据______) ∴
即点B是线段AC的中点.
21.(本题7分)如图,已知D为△ABC的BC边的中点,DE、DF分别平分∠ADB和∠ADC,
求证:BE+CF>EF.
22.(本题7分)为进一步打造“宜居重庆”,某区拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请在答题卷的原图上利用尺规作图作出音乐喷泉M的位置.(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
23.(本题7分)如图,已知,.
求证:;
若,问经过怎样的变换能与重合?
24.(本题7分)如图,在长方形ABCD中,AB=4,AD=6,延长BC到点E,使CE=2,连结DE,动点P从点B出发,以每秒2个单位的速度沿BC→CD→DA向终点A运动,设点P的运动时间为t(s),当t为何值时,△ABP和△DCE全等?
参考答案
1.C
【详解】
A. 作直线AB的垂线为描叙性语言,不是命题,故错误;
B. 在线段AB上取点C为描叙性语言,不是命题,故错误;
C. 同旁内角互补为命题,故正确;
D. 垂线段最短吗为疑问句,不是命题,故错误.
2.D
【详解】
解:命题“垂直于同一条直线的两条直线互相平行”的条件是两条直线垂直于同一条直线,
3.C
【解析】解:两边及夹角对应相等的两个三角形全等,这为“边角边”定理,简写成“SAS”.故选C.
4.C
【详解】
A.∵2+3>4,∴能组成三角形,故A错误;
B.∵5+7>7,∴不能组成三角形,故B错误;
C.∵5+6<12,∴不能组成三角形,故C正确;
D.∵6+8>10,∴能组成三角形,故D错误;
5.A
【详解】
∵如图,AE⊥AB且AE=AB,EF⊥FH,BG⊥FH?∠EAB=∠EFA=∠BGA=90?,∠EAF+∠BAG=90?,∠ABG+∠BAG=90??∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG?△EFA≌△AGB,
∴AF=BG,AG=EF.
同理证得△BGC≌△CHD得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16
故S= (6+4)×16?3×4?6×3=50.
故选A.
6.A
【详解】
∵点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C.
∴PA=PC,
∴△ABP≌△CBP ,△ABD≌△CBD ,
∴∠ADB=∠CDB,
故选A.
7.B
【解析】
根据全等三角形的判定SAS,可知两条直角边对应相等的两个直角三角形全等,故A不正确;
根据一条直角边和斜边对应相等的两个直角三角形,符合全等三角形的判定定理HL,能判定全等;若两条直角边对应相等的两个直角三角形,符合全等三角形的判定定理SAS,也能判全等,但是有两边对应相等,没说明是什么边对应,故不能判定,故B正确.
根据全等三角形的判定AAS,可知斜边和一锐角对应相等的两直角三角形全等,故C不正确;
根据直角三角形的判定HL,可知一条直角边和斜边对应相等两直角三角形全等,故D不正确.
故选B.
8.B
【详解】
∵∠1+∠2=90°,∠3+∠2=90°,
∴∠1=∠3,①正确;
∵∠2=30°,
∴∠1=60°,
又∵∠E=60°,
∴∠1=∠E,
∴AC∥DE,②正确;
∵∠2=30°,
∴∠1+∠2+∠3=150°,
又∵∠C=45°,
∴BC与AD不平行,③错误;
∵∠2=30°,
∴AC∥DE,
∴∠4=∠C,④正确.
9.B
【详解】
∵AD是∠CAB的角平分线,DE⊥AB,∠C=90°,
∴DC=DE,AC=AE,
∴△DEB的周长=DE+BE+BD=BE+DC+BD=BE+BC=BE+AE=AB=6cm,
10.C
【详解】
试题分析:如图,过点E作EF⊥BC交BC于点F,根据角平分线的性质可得DE=EF=2,所以△BCE的面积等于,故答案选C.
考点:角平分线的性质;三角形的面积公式.
11.△ADC, △BCD , △ADB, △BCA
【解析】
试题解析:在△ADC和△BCD中;
∴△ADC≌△BCD(SSS).
在△ADB和△BCA中;
∴△ADB≌△BCA(SSS).
故答案为:△ADC,△BCD;△ADB,△BCA.
点睛:三条边对应相等,两个三角形全等.
12.1
延长AD至E,使DE=AD,连接CE,
在△ABD与△ECD中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=10,
在△ACE中,CE-AC<AE<CE+AC,AC=8,
即2<2AD<18,
1<AD<9,
13.∠BAC=∠DAC(答案不唯一)
【解析】
添加的条件是:∠ACB=∠ACD,理由:∵ ∠ACB=∠ACD,∠B=∠D,AC=AC,∴ △ABC≌△ADC;添加的条件是:∠BAC=∠DAC,理由:∵ ∠BAC=∠DAC,∠B=∠D,AC=AC;∴ △ABC≌△ADC.
14.3
【详解】
根据对顶角相等和线段的中点的定义,运用SAS可得△AOE≌△BOF,△AOC≌△BOD,△COE≌△DOF,共3对.做题时从已知开始结合全等的判定方法由易到难逐个找寻.
故答案为3.
15.70°
【详解】
由等腰三角形的性质得出∠B=∠C=70°,再根据SAS证得△BDE≌△CEF,得出∠BDE=∠CEF,运用三角形的外角性质得出∠CEF+∠DEF=∠B+∠BDE,即可得出∠DEF=∠B=70°.
16.2
【详解】
根据题意,可得三种命题,由①②③,根据直角三角形全等的判定HL可证明,是真命题;由①③②,能证明∠ABC=∠ADC,但是不能得出一定是90°,是假命题;由②③①,根据SAS可证明两三角形全等,再根据全等三角形的性质可证明,故是真命题.因此可知真命题有2个.
故答案为2.
17.AB=CD ∠DAC=∠BCA
【解析】
∵在△ABC和△CDA中,
∴△ABC≌△CDA(SSS);
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
故答案为AB=CD,∠DAC=∠BCA.
18.证明:是的中点
,
在和中,
,
,
,
(SAS),
.
19.(1)见解析;(2)6
【详解】
证明:(1)证明:∵DB⊥BC,CF⊥AE,
∴∠DCB+∠D=∠DCB+∠AEC=90°.
∴∠D=∠AEC.
又∵∠DBC=∠ECA=90°,且BC=CA,
在△DBC和△ECA中,
∴△DBC≌△ECA(AAS).
∴AE=CD;
(2) 由(1)可得△DBC≌△ECA
∴CE=BD,
∵BC=AC=12cm AE是BC的中线,
∴,
∴BD=6cm.
20.
【详解】
证明:在和中
∴≌()
∴.
在和中
∴≌(根据)
∴
即点B是线段AC的中点.
21.证明见解析.
【解析】
试题分析:在 DA 上取一点 M ,使 DM=DB=DC ,连结 EM 、 MF ,实质上是将△DBE 及△DFC 分别沿 DE 、 DF 翻折 180° 得到△DEM 及△MFD ,从而使问题得到解决的 .
试题解析:在 DA 上取一点 M ,使 DM=DB=DC ,连结 EM 、 MF ,
∵ DE 平分∠ADB ,
∴ ∠BDE= ∠EDM.
又∵ DM=BD , DE=DE ,
∴ △BED ≌△MED.
同理可得△MFD ≌△CFD.
∴ BE=EM , CF=MF.
∵ 在△EMF 中, EM+MF>EF.
∴ BE+CF>EF.
22.解:作AB的垂直平分线,以点C为圆心,以AB的一半为半径画弧交AB的垂直平分线于点M即可.
【详解】
易得M在AB的垂直平分线上,且到C的距离等于AB的一半.
23.(1)见解析;(2)先将绕点逆时针旋转,再将沿直线对折,即可得与重合.或先将绕点顺时针旋转,再将沿直线对折,即可得与重合
【分析】
(1)要证明∠B=∠C,可以证明它们所在的三角形全等,即证明△ABE≌△ACD;已知两边和它们的夹角对应相等,由SAS即可判定两三角形全等.
(2)因为△ABE≌△ACD,公共点A,对应线段CD与BE相交,所以要通过旋转,翻折两次完成.
【详解】
在与中,,,;
∴,
∴.
先将绕点逆时针旋转,
再将沿直线对折,即可得与重合.
或先将绕点顺时针旋转,
再将沿直线对折,即可得与重合.
24.当t=1或7时,△ABP和△DCE全等
【详解】
试题分析:由条件可以知道BP=2t,当点P在线段BC上时,可以知道BP=CE,当点P在线段DA上时,有AD=CE,分别可得到关于t的方程,可求得t的值.
试题解析:∵AB=CD,∠A=∠B=∠DCE=90°,
∴△ABP≌△DCE或△BAP≌△DCE.
当△ABP≌△DCE时,BP=CE=2,
此时2t=2,解得t=1.
当△BAP≌△DCE时,AP=CE=2,
此时BC+CD+DP=BC+CD+(DA-AP)=6+4+(6-2)=14,即2t=14,解得t=7.
∴当t=1或7时,△ABP和△DCE全等.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
