2.4 等腰三角形的判定定理 同步练习(含详解)
文档属性
| 名称 | 2.4 等腰三角形的判定定理 同步练习(含详解) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版八年级上2.4等腰三角形的判定定理同步练习
一.选择题
1.(2019秋?来宾期末)如图,△ABC中,∠ABC,∠ACB的平分线相交于O,MN过点O且与BC平行,△ABC的周长为20,△AMN的周长为12,则BC的长为( )
A.8
B.4
C.32
D.16
2.(2020秋?临沭县期中)下列给出的5个图中,能判定△ABC是等腰三角形的有( )
A.2个
B.3个
C.4个
D.5个
3.(2019秋?樊城区期中)上午8时,一条船从海岛A出发,以15n
mile/h(海里/时,1n
mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.则从海岛B到灯塔C的距离为( )
A.45n
mile
B.30n
mile
C.20n
mile
D.15n
mile
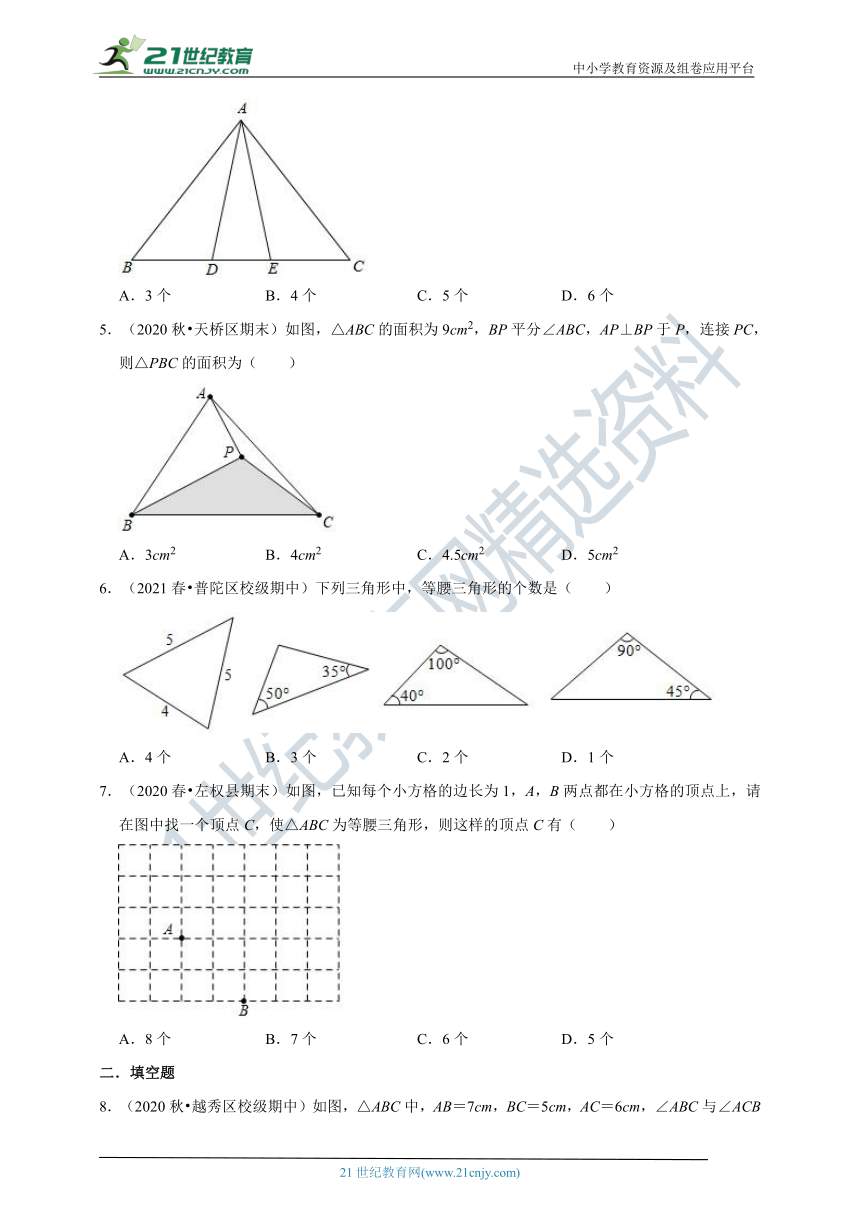
4.(2020秋?西湖区校级期中)如图,在△ABC中,AB=AC,∠BAC=108°,BD=AD=AE,则图中等腰三角形的个数为( )
A.3个
B.4个
C.5个
D.6个
5.(2020秋?天桥区期末)如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为( )
A.3cm2
B.4cm2
C.4.5cm2
D.5cm2
6.(2021春?普陀区校级期中)下列三角形中,等腰三角形的个数是( )
A.4个
B.3个
C.2个
D.1个
7.(2020春?左权县期末)如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
A.8个
B.7个
C.6个
D.5个
二.填空题
8.(2020秋?越秀区校级期中)如图,△ABC中,AB=7cm,BC=5cm,AC=6cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,则△ADE的周长=
cm.
9.(2020秋?南关区校级期末)如图,△PBC的面积为4cm2,AP垂直∠B的平分线BP于点P,则△ABC的面积为
cm2.
10.(2019春?乐清市期中)在△ABC中,∠BAC=126°,AD是BC边上的高,若AB+BD=DC,则∠C=
.
11.(2019?松北区二模)如图,在△ABC中,AE⊥BC于E,点D为BC边中点,AF⊥AB交BC边于点F,∠C=2∠B,若DE=4,CF=2,则CE=
.
12.如图,在△ABC中,∠CAB=120°,AB=AC=4,∠BAC的平分线交BC于D,DF∥AB交∠BAD的平分线于F,则DF=
.
三.解答题
13.(2020秋?盐池县期末)已知:如图,AC=AB,∠ACD=∠ABD,求证:CD=BD.
14.如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
15.(2020秋?下城区期末)如图,在△ABC中,AB=AC.过点A作BC的平行线交∠ABC的角平分线于点D,连接CD.
(1)求证:△ACD为等腰三角形.
(2)若∠BAD=140°,求∠BDC的度数.
16.(2018秋?如皋市期中)在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:
①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.
(1)上述4个条件中,由哪两个条件可以判定△AED是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
17.(2020秋?大安市期末)已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC﹣AB=2BE.
答案与解析
一.选择题
1.(2019秋?来宾期末)如图,△ABC中,∠ABC,∠ACB的平分线相交于O,MN过点O且与BC平行,△ABC的周长为20,△AMN的周长为12,则BC的长为( )
A.8
B.4
C.32
D.16
【解析】解:∵OB平分∠MBC,
∴∠MBO=∠OBC,
又MN∥BC,
∴∠MOB=∠OBC,
∴∠MOB=∠MBO,
∴MB=MO,同理可得∠NOC=∠NCO,
∴NO=NC,
∴(AB+AC+BC)﹣(AM+AN+MN)
=(AM+MB+AN+NC+BC)﹣(AM+AN+MN)
=(AM+MO+AN+NO+BC)﹣(AM+AN+MN)
=(AM+AN+MN+BC)﹣(AM+AN+MN)
=BC,
又∵△ABC的周长为20,△AMN的周长为12,即AB+AC+BC=20,AM+AN+MN=12,
则BC=20﹣12=8.
故选:A.
2.(2020秋?临沭县期中)下列给出的5个图中,能判定△ABC是等腰三角形的有( )
A.2个
B.3个
C.4个
D.5个
【解析】解:图①中,∵∠C=180°﹣∠A﹣∠B=180°﹣70°﹣66°=44°,
∴∠A≠∠B≠∠C,
∴△ABC不是等腰三角形;
图②中,∵∠B+∠C=140°,∠B=70°,
∴∠C=140°﹣70°=70°,
∴∠B=∠C,
∴△ABC是等腰三角形;
图③中,∵AD∥BC,
∴∠C=∠CAD=50°,
∵∠B=50°,
∴∠B=∠C,
∴△ABC是等腰三角形;
图④中,∵AD∥BC,
∴∠BCA=∠CAD=30°,∠BAD=180°﹣∠B=180°﹣120°=60°,
∴∠BAC=60°﹣30°=30°,
∴∠BAC=∠BCA,
∴△ABC是等腰三角形;
图⑤中,∵AB∥DE,
∴∠A=∠D=30°,
∵∠BCD=∠A+∠B=60°,
∴∠B=60°﹣∠A=30°,
∴∠B=∠A,
∴△ABC是等腰三角形;
能判定△ABC是等腰三角形的有4个,
故选:C.
3.(2019秋?樊城区期中)上午8时,一条船从海岛A出发,以15n
mile/h(海里/时,1n
mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.则从海岛B到灯塔C的距离为( )
A.45n
mile
B.30n
mile
C.20n
mile
D.15n
mile
【解析】解:∵∠NBC=84°,∠NAC=42°,
∴∠C=84°﹣42°=42°.
∴∠C=∠NAC,
∴BC=AB,
∵上午8时,一条船从海岛A出发,以150n
mile/h的速度向正北航行.10时到达海岛B处,
∴BC=AB=15×2=30n
mile.
故选:B.
4.(2020秋?西湖区校级期中)如图,在△ABC中,AB=AC,∠BAC=108°,BD=AD=AE,则图中等腰三角形的个数为( )
A.3个
B.4个
C.5个
D.6个
【解析】解:∵AB=AC,∠BAC=108°,
∴△ABC是等腰三角形,∠B=∠C=(180°﹣108°)=36°,
∵BD=AD=AE,
∴△ABD、△ADE是等腰三角形,∠DAB=∠B=36°,∠AED=∠ADE=∠B+∠DAB=72°,
∴∠EAC=∠AED﹣∠C=72°﹣36°=36°,
∴∠EAC=∠C,
∴△ACE是等腰三角形,AE=CE,
∵∠DAE=180°﹣∠ADE﹣∠AED=180°﹣72°﹣72°=36°,
∴∠BAE=∠DAB+∠DAE=72°,
∴∠BAE=∠AED,
∴△BAE是等腰三角形,BA=BE,
同理:△CAD是等腰三角形,
则图中等腰三角形的个数为6个,
故选:D.
5.(2020秋?天桥区期末)如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为( )
A.3cm2
B.4cm2
C.4.5cm2
D.5cm2
【解析】解:延长AP交BC于E,
∵BP平分∠ABC,
∴∠ABP=∠EBP,
∵AP⊥BP,
∴∠APB=∠EPB=90°,
在△ABP和△EBP中,,
∴△ABP≌△EBP(ASA),
∴AP=PE,
∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC=×9cm2=4.5cm2,
故选:C.
6.(2021春?普陀区校级期中)下列三角形中,等腰三角形的个数是( )
A.4个
B.3个
C.2个
D.1个
【解析】解:第一个图形中有两边相等,故第一个三角形是等腰三角形,
第二个图形中的三个角分别为50°,35°,95°,故第二个三角形不是等腰三角形;
第三个图形中的三个角分别为100°,40°,40°,故第三个三角形是等腰三角形;
第四个图形中的三个角分别为90°,45°,45°,故第四个三角形是等腰三角形;
故选:B.
7.(2020春?左权县期末)如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
A.8个
B.7个
C.6个
D.5个
【解析】解:当AB为底时,作AB的垂直平分线,可找出格点C的个数有5个,
当AB为腰时,分别以A、B点为顶点,以AB为半径作弧,可找出格点C的个数有3个;
∴这样的顶点C有8个.
故选:A.
二.填空题
8.(2020秋?越秀区校级期中)如图,△ABC中,AB=7cm,BC=5cm,AC=6cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,则△ADE的周长= 13 cm.
【解析】解:如图,
∵OB、OC分别平分∠ABC与∠ACB,
∴∠1=∠2,∠3=∠4,
而DE∥BC,
∴∠2=∠5,∠6=∠4,
∴∠1=∠5,∠6=∠3,
∴DO=DB,EO=EC,
∴△ADE的周长=AD+DO+AE+EO=AD+DB+AE+EC=AB+AC=7+6=13(cm).
故答案为13.
9.(2020秋?南关区校级期末)如图,△PBC的面积为4cm2,AP垂直∠B的平分线BP于点P,则△ABC的面积为 8 cm2.
【解析】解:如图,延长AP交BC于点Q,
∵AP垂直∠ABC的平分线BP于P,
∴AP=QP,
∴S△ABP=S△BQP,S△APC=S△PQC,
∴S△ABC=2S阴影=8(cm2),
故答案为:8.
10.(2019春?乐清市期中)在△ABC中,∠BAC=126°,AD是BC边上的高,若AB+BD=DC,则∠C= 18° .
【解析】解:在线段DC上取一点E,使DE=DB,连接AE,
∵AD⊥BC,
∴AD垂直平分BE,
∴AB=AE,
∴∠AEB=∠B,
∵AB+BD=DC,
∴AE=CE,
∴∠EAC=∠C,
∵∠AEB=∠EAC+∠C=2∠C,
∴∠B=2∠C,
∵∠BAC=126°,
∴∠B+∠C=180°﹣126°=54°,
∴∠C=18°,
故答案为:18°
11.(2019?松北区二模)如图,在△ABC中,AE⊥BC于E,点D为BC边中点,AF⊥AB交BC边于点F,∠C=2∠B,若DE=4,CF=2,则CE= 5 .
【解析】解:取BF的中点G,连接AG,如图所示:
则BG=FG,
∵AF⊥AB,
∴∠BAF=90°,
∴AG=BF=BG=FG,
∴∠B=∠GAB,
∵∠AGC=∠B+∠GAB=2∠B,∠C=2∠B,
∴∠AGC=∠C,
∴AG=AC,
∵AE⊥BC,
∴GE=CE,
∵点D为BC边中点,
∴BD=CD,
设EF=x,则GE=CE=EF+CF=x+2,BD=CD=DE+EF+CF=x+6,DG=GE﹣DE=x﹣2,
∴BG=FG=GE+EF=2x+2,
∵BD=CD,
∴2x+2+x﹣2=x+6,
解得:x=3,
∴EF=3,
∴CE=EF+CF=5;
故答案为:5.
12.如图,在△ABC中,∠CAB=120°,AB=AC=4,∠BAC的平分线交BC于D,DF∥AB交∠BAD的平分线于F,则DF= 2 .
【解析】解:∵△ABC是等腰三角形,D为底边的中点,
∴AD⊥BC,∠BAD=∠CAD,
∵∠BAC=120°,
∴∠BAD=60°,∠ADB=90°,
∵AE是∠BAD的角平分线,
∴∠DAE=∠EAB=30°.
∵DF∥AB,
∴∠F=∠BAE=30°.
∴∠DAF=∠F=30°,
∴AD=DF.
∵AB=4,∠B=30°,
∴AD=2,
∴DF=2.
故答案为:2.
三.解答题
13.(2020秋?盐池县期末)已知:如图,AC=AB,∠ACD=∠ABD,求证:CD=BD.
【解析】证明:连接BC,
∵AC=AB,
∴∠ACB=∠ABC;
∵∠DCB=∠ACD﹣∠ACB,
∠DBC=∠ABD﹣∠ABC,而∠ACD=∠ABD,
∴∠DCB=∠DBC,
∴CD=BD.
14.如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
【解析】证明:在△ABE和△ACD中,,
∴△ABE≌△ACD(AAS),
∴AB=AC,
∴∠ABC=∠ACB,
∴∠ABC﹣∠1=∠ACB﹣∠2,
即∠FBC=∠FCB,
∴BF=CF.
15.(2020秋?下城区期末)如图,在△ABC中,AB=AC.过点A作BC的平行线交∠ABC的角平分线于点D,连接CD.
(1)求证:△ACD为等腰三角形.
(2)若∠BAD=140°,求∠BDC的度数.
【解析】(1)证明:∵BD平分∠ABC,
∴∠1=∠2.
∵AD∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴AB=AD.
∵AB=AC,
∴AC=AD,
∴△ACD为等腰三角形;
(2)解:由(1)知,∠1=∠2=∠3,
∵∠BAD=140°,∠BAD+∠1+∠3=180°,
∴∠1=∠2=∠3=(180°﹣∠BAD)=20°,
∠ABC=40°,
∵AB=AC,
∴∠ACB=∠ABC=40°,
由(1)知,AD=AC,
∴∠ACD=∠ADC=∠BDC+∠3=∠BDC+20°,
∵AD∥BC,
∴∠ADC+∠ACD=180°,
∴40°+(∠BDC+20°)+(∠BDC+20°)=180°,
∴∠BDC=50°.
16.(2018秋?如皋市期中)在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:
①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.
(1)上述4个条件中,由哪两个条件可以判定△AED是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
【解析】解:(1)①③、①④、②③、②④都可以证明△ABE≌△DCE,可得到AE=DE,可判定△AED为等腰三角形;
(2)选择①③,证明如下:
在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AE=DE,
∴△AED为等腰三角形.
17.(2020秋?大安市期末)已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC﹣AB=2BE.
【解析】证明:延长BE交AC于M
∵BE⊥AE,
∴∠AEB=∠AEM=90°
在△ABE中,
∵∠1+∠3+∠AEB=180°,
∴∠3=90°﹣∠1
同理,∠4=90°﹣∠2
∵∠1=∠2,
∴∠3=∠4,
∴AB=AM
∵BE⊥AE,
∴BM=2BE,
∴AC﹣AB=AC﹣AM=CM,
∵∠4是△BCM的外角
∴∠4=∠5+∠C
∵∠ABC=3∠C,∴∠ABC=∠3+∠5=∠4+∠5
∴3∠C=∠4+∠5=2∠5+∠C
∴∠5=∠C
∴CM=BM
∴AC﹣AB=BM=2BE
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版八年级上2.4等腰三角形的判定定理同步练习
一.选择题
1.(2019秋?来宾期末)如图,△ABC中,∠ABC,∠ACB的平分线相交于O,MN过点O且与BC平行,△ABC的周长为20,△AMN的周长为12,则BC的长为( )
A.8
B.4
C.32
D.16
2.(2020秋?临沭县期中)下列给出的5个图中,能判定△ABC是等腰三角形的有( )
A.2个
B.3个
C.4个
D.5个
3.(2019秋?樊城区期中)上午8时,一条船从海岛A出发,以15n
mile/h(海里/时,1n
mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.则从海岛B到灯塔C的距离为( )
A.45n
mile
B.30n
mile
C.20n
mile
D.15n
mile
4.(2020秋?西湖区校级期中)如图,在△ABC中,AB=AC,∠BAC=108°,BD=AD=AE,则图中等腰三角形的个数为( )
A.3个
B.4个
C.5个
D.6个
5.(2020秋?天桥区期末)如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为( )
A.3cm2
B.4cm2
C.4.5cm2
D.5cm2
6.(2021春?普陀区校级期中)下列三角形中,等腰三角形的个数是( )
A.4个
B.3个
C.2个
D.1个
7.(2020春?左权县期末)如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
A.8个
B.7个
C.6个
D.5个
二.填空题
8.(2020秋?越秀区校级期中)如图,△ABC中,AB=7cm,BC=5cm,AC=6cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,则△ADE的周长=
cm.
9.(2020秋?南关区校级期末)如图,△PBC的面积为4cm2,AP垂直∠B的平分线BP于点P,则△ABC的面积为
cm2.
10.(2019春?乐清市期中)在△ABC中,∠BAC=126°,AD是BC边上的高,若AB+BD=DC,则∠C=
.
11.(2019?松北区二模)如图,在△ABC中,AE⊥BC于E,点D为BC边中点,AF⊥AB交BC边于点F,∠C=2∠B,若DE=4,CF=2,则CE=
.
12.如图,在△ABC中,∠CAB=120°,AB=AC=4,∠BAC的平分线交BC于D,DF∥AB交∠BAD的平分线于F,则DF=
.
三.解答题
13.(2020秋?盐池县期末)已知:如图,AC=AB,∠ACD=∠ABD,求证:CD=BD.
14.如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
15.(2020秋?下城区期末)如图,在△ABC中,AB=AC.过点A作BC的平行线交∠ABC的角平分线于点D,连接CD.
(1)求证:△ACD为等腰三角形.
(2)若∠BAD=140°,求∠BDC的度数.
16.(2018秋?如皋市期中)在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:
①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.
(1)上述4个条件中,由哪两个条件可以判定△AED是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
17.(2020秋?大安市期末)已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC﹣AB=2BE.
答案与解析
一.选择题
1.(2019秋?来宾期末)如图,△ABC中,∠ABC,∠ACB的平分线相交于O,MN过点O且与BC平行,△ABC的周长为20,△AMN的周长为12,则BC的长为( )
A.8
B.4
C.32
D.16
【解析】解:∵OB平分∠MBC,
∴∠MBO=∠OBC,
又MN∥BC,
∴∠MOB=∠OBC,
∴∠MOB=∠MBO,
∴MB=MO,同理可得∠NOC=∠NCO,
∴NO=NC,
∴(AB+AC+BC)﹣(AM+AN+MN)
=(AM+MB+AN+NC+BC)﹣(AM+AN+MN)
=(AM+MO+AN+NO+BC)﹣(AM+AN+MN)
=(AM+AN+MN+BC)﹣(AM+AN+MN)
=BC,
又∵△ABC的周长为20,△AMN的周长为12,即AB+AC+BC=20,AM+AN+MN=12,
则BC=20﹣12=8.
故选:A.
2.(2020秋?临沭县期中)下列给出的5个图中,能判定△ABC是等腰三角形的有( )
A.2个
B.3个
C.4个
D.5个
【解析】解:图①中,∵∠C=180°﹣∠A﹣∠B=180°﹣70°﹣66°=44°,
∴∠A≠∠B≠∠C,
∴△ABC不是等腰三角形;
图②中,∵∠B+∠C=140°,∠B=70°,
∴∠C=140°﹣70°=70°,
∴∠B=∠C,
∴△ABC是等腰三角形;
图③中,∵AD∥BC,
∴∠C=∠CAD=50°,
∵∠B=50°,
∴∠B=∠C,
∴△ABC是等腰三角形;
图④中,∵AD∥BC,
∴∠BCA=∠CAD=30°,∠BAD=180°﹣∠B=180°﹣120°=60°,
∴∠BAC=60°﹣30°=30°,
∴∠BAC=∠BCA,
∴△ABC是等腰三角形;
图⑤中,∵AB∥DE,
∴∠A=∠D=30°,
∵∠BCD=∠A+∠B=60°,
∴∠B=60°﹣∠A=30°,
∴∠B=∠A,
∴△ABC是等腰三角形;
能判定△ABC是等腰三角形的有4个,
故选:C.
3.(2019秋?樊城区期中)上午8时,一条船从海岛A出发,以15n
mile/h(海里/时,1n
mile=1852m)的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得NAC=42°,NBC=84°.则从海岛B到灯塔C的距离为( )
A.45n
mile
B.30n
mile
C.20n
mile
D.15n
mile
【解析】解:∵∠NBC=84°,∠NAC=42°,
∴∠C=84°﹣42°=42°.
∴∠C=∠NAC,
∴BC=AB,
∵上午8时,一条船从海岛A出发,以150n
mile/h的速度向正北航行.10时到达海岛B处,
∴BC=AB=15×2=30n
mile.
故选:B.
4.(2020秋?西湖区校级期中)如图,在△ABC中,AB=AC,∠BAC=108°,BD=AD=AE,则图中等腰三角形的个数为( )
A.3个
B.4个
C.5个
D.6个
【解析】解:∵AB=AC,∠BAC=108°,
∴△ABC是等腰三角形,∠B=∠C=(180°﹣108°)=36°,
∵BD=AD=AE,
∴△ABD、△ADE是等腰三角形,∠DAB=∠B=36°,∠AED=∠ADE=∠B+∠DAB=72°,
∴∠EAC=∠AED﹣∠C=72°﹣36°=36°,
∴∠EAC=∠C,
∴△ACE是等腰三角形,AE=CE,
∵∠DAE=180°﹣∠ADE﹣∠AED=180°﹣72°﹣72°=36°,
∴∠BAE=∠DAB+∠DAE=72°,
∴∠BAE=∠AED,
∴△BAE是等腰三角形,BA=BE,
同理:△CAD是等腰三角形,
则图中等腰三角形的个数为6个,
故选:D.
5.(2020秋?天桥区期末)如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为( )
A.3cm2
B.4cm2
C.4.5cm2
D.5cm2
【解析】解:延长AP交BC于E,
∵BP平分∠ABC,
∴∠ABP=∠EBP,
∵AP⊥BP,
∴∠APB=∠EPB=90°,
在△ABP和△EBP中,,
∴△ABP≌△EBP(ASA),
∴AP=PE,
∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC=×9cm2=4.5cm2,
故选:C.
6.(2021春?普陀区校级期中)下列三角形中,等腰三角形的个数是( )
A.4个
B.3个
C.2个
D.1个
【解析】解:第一个图形中有两边相等,故第一个三角形是等腰三角形,
第二个图形中的三个角分别为50°,35°,95°,故第二个三角形不是等腰三角形;
第三个图形中的三个角分别为100°,40°,40°,故第三个三角形是等腰三角形;
第四个图形中的三个角分别为90°,45°,45°,故第四个三角形是等腰三角形;
故选:B.
7.(2020春?左权县期末)如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
A.8个
B.7个
C.6个
D.5个
【解析】解:当AB为底时,作AB的垂直平分线,可找出格点C的个数有5个,
当AB为腰时,分别以A、B点为顶点,以AB为半径作弧,可找出格点C的个数有3个;
∴这样的顶点C有8个.
故选:A.
二.填空题
8.(2020秋?越秀区校级期中)如图,△ABC中,AB=7cm,BC=5cm,AC=6cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB、AC于点D、E,则△ADE的周长= 13 cm.
【解析】解:如图,
∵OB、OC分别平分∠ABC与∠ACB,
∴∠1=∠2,∠3=∠4,
而DE∥BC,
∴∠2=∠5,∠6=∠4,
∴∠1=∠5,∠6=∠3,
∴DO=DB,EO=EC,
∴△ADE的周长=AD+DO+AE+EO=AD+DB+AE+EC=AB+AC=7+6=13(cm).
故答案为13.
9.(2020秋?南关区校级期末)如图,△PBC的面积为4cm2,AP垂直∠B的平分线BP于点P,则△ABC的面积为 8 cm2.
【解析】解:如图,延长AP交BC于点Q,
∵AP垂直∠ABC的平分线BP于P,
∴AP=QP,
∴S△ABP=S△BQP,S△APC=S△PQC,
∴S△ABC=2S阴影=8(cm2),
故答案为:8.
10.(2019春?乐清市期中)在△ABC中,∠BAC=126°,AD是BC边上的高,若AB+BD=DC,则∠C= 18° .
【解析】解:在线段DC上取一点E,使DE=DB,连接AE,
∵AD⊥BC,
∴AD垂直平分BE,
∴AB=AE,
∴∠AEB=∠B,
∵AB+BD=DC,
∴AE=CE,
∴∠EAC=∠C,
∵∠AEB=∠EAC+∠C=2∠C,
∴∠B=2∠C,
∵∠BAC=126°,
∴∠B+∠C=180°﹣126°=54°,
∴∠C=18°,
故答案为:18°
11.(2019?松北区二模)如图,在△ABC中,AE⊥BC于E,点D为BC边中点,AF⊥AB交BC边于点F,∠C=2∠B,若DE=4,CF=2,则CE= 5 .
【解析】解:取BF的中点G,连接AG,如图所示:
则BG=FG,
∵AF⊥AB,
∴∠BAF=90°,
∴AG=BF=BG=FG,
∴∠B=∠GAB,
∵∠AGC=∠B+∠GAB=2∠B,∠C=2∠B,
∴∠AGC=∠C,
∴AG=AC,
∵AE⊥BC,
∴GE=CE,
∵点D为BC边中点,
∴BD=CD,
设EF=x,则GE=CE=EF+CF=x+2,BD=CD=DE+EF+CF=x+6,DG=GE﹣DE=x﹣2,
∴BG=FG=GE+EF=2x+2,
∵BD=CD,
∴2x+2+x﹣2=x+6,
解得:x=3,
∴EF=3,
∴CE=EF+CF=5;
故答案为:5.
12.如图,在△ABC中,∠CAB=120°,AB=AC=4,∠BAC的平分线交BC于D,DF∥AB交∠BAD的平分线于F,则DF= 2 .
【解析】解:∵△ABC是等腰三角形,D为底边的中点,
∴AD⊥BC,∠BAD=∠CAD,
∵∠BAC=120°,
∴∠BAD=60°,∠ADB=90°,
∵AE是∠BAD的角平分线,
∴∠DAE=∠EAB=30°.
∵DF∥AB,
∴∠F=∠BAE=30°.
∴∠DAF=∠F=30°,
∴AD=DF.
∵AB=4,∠B=30°,
∴AD=2,
∴DF=2.
故答案为:2.
三.解答题
13.(2020秋?盐池县期末)已知:如图,AC=AB,∠ACD=∠ABD,求证:CD=BD.
【解析】证明:连接BC,
∵AC=AB,
∴∠ACB=∠ABC;
∵∠DCB=∠ACD﹣∠ACB,
∠DBC=∠ABD﹣∠ABC,而∠ACD=∠ABD,
∴∠DCB=∠DBC,
∴CD=BD.
14.如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
【解析】证明:在△ABE和△ACD中,,
∴△ABE≌△ACD(AAS),
∴AB=AC,
∴∠ABC=∠ACB,
∴∠ABC﹣∠1=∠ACB﹣∠2,
即∠FBC=∠FCB,
∴BF=CF.
15.(2020秋?下城区期末)如图,在△ABC中,AB=AC.过点A作BC的平行线交∠ABC的角平分线于点D,连接CD.
(1)求证:△ACD为等腰三角形.
(2)若∠BAD=140°,求∠BDC的度数.
【解析】(1)证明:∵BD平分∠ABC,
∴∠1=∠2.
∵AD∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴AB=AD.
∵AB=AC,
∴AC=AD,
∴△ACD为等腰三角形;
(2)解:由(1)知,∠1=∠2=∠3,
∵∠BAD=140°,∠BAD+∠1+∠3=180°,
∴∠1=∠2=∠3=(180°﹣∠BAD)=20°,
∠ABC=40°,
∵AB=AC,
∴∠ACB=∠ABC=40°,
由(1)知,AD=AC,
∴∠ACD=∠ADC=∠BDC+∠3=∠BDC+20°,
∵AD∥BC,
∴∠ADC+∠ACD=180°,
∴40°+(∠BDC+20°)+(∠BDC+20°)=180°,
∴∠BDC=50°.
16.(2018秋?如皋市期中)在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:
①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.
(1)上述4个条件中,由哪两个条件可以判定△AED是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
【解析】解:(1)①③、①④、②③、②④都可以证明△ABE≌△DCE,可得到AE=DE,可判定△AED为等腰三角形;
(2)选择①③,证明如下:
在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AE=DE,
∴△AED为等腰三角形.
17.(2020秋?大安市期末)已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC﹣AB=2BE.
【解析】证明:延长BE交AC于M
∵BE⊥AE,
∴∠AEB=∠AEM=90°
在△ABE中,
∵∠1+∠3+∠AEB=180°,
∴∠3=90°﹣∠1
同理,∠4=90°﹣∠2
∵∠1=∠2,
∴∠3=∠4,
∴AB=AM
∵BE⊥AE,
∴BM=2BE,
∴AC﹣AB=AC﹣AM=CM,
∵∠4是△BCM的外角
∴∠4=∠5+∠C
∵∠ABC=3∠C,∴∠ABC=∠3+∠5=∠4+∠5
∴3∠C=∠4+∠5=2∠5+∠C
∴∠5=∠C
∴CM=BM
∴AC﹣AB=BM=2BE
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
