1.2 二次函数的图像 培优强化 2021-2022学年浙教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 1.2 二次函数的图像 培优强化 2021-2022学年浙教版九年级数学上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 183.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 10:29:07 | ||
图片预览



文档简介
1.2 二次函数的图象
1.已知二次函数y=ax2的图象过点(-1,3),则a的值为( )
A.-3 B.3 C. D.-
2.若抛物线y=(2m-1)x2的开口向下,则m的取值范围是( )
A.m<0 B.m<
C.m> D.m>-
3.已知正方形的边长为x(cm),则它的面积y(cm2)与边长x(cm)的函数关系可表示为图中的( )
4.将函数y=kx2与y=kx+k的图象画在同一直角坐标系中,可能的是( )
5.抛物线y=(x+3)2+1的顶点坐标是( )
A.(-3,1) B.(-3,-1)
C.(3,-1) D.(3,1)
6.在同一坐标平面内,图象不可能由函数y=2x2+1的图象通过平移变换或轴对称变换得到的函数是( )
A.y=2(x+1)2-1 B.y=2x2+3
C.y=-2x2-1
D.y=x2-1
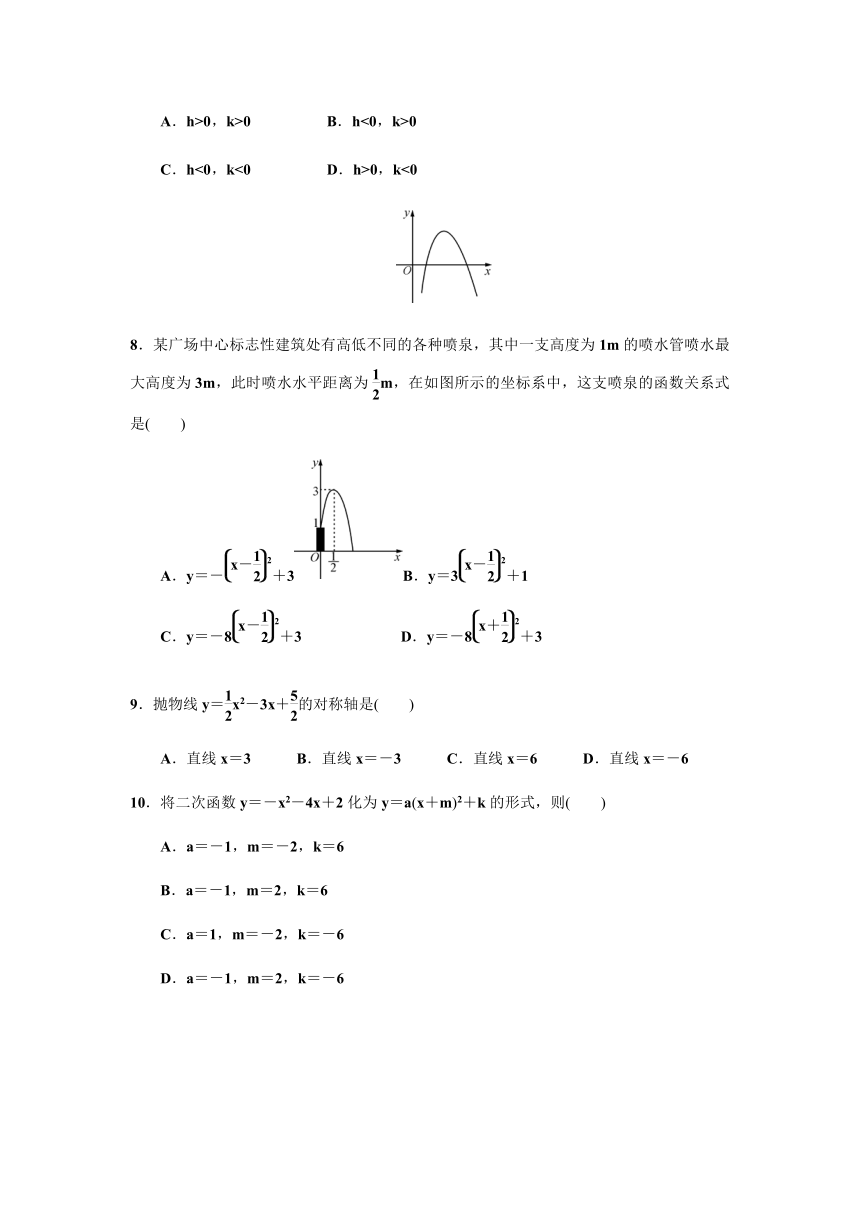
7.如图,在平面直角坐标系中,抛物线所表示的函数解析式为y=-2(x-h)2+k,则下列结论正确的是( )
A.h>0,k>0
B.h<0,k>0
C.h<0,k<0
D.h>0,k<0
8.某广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为1m的喷水管喷水最大高度为3m,此时喷水水平距离为m,在如图所示的坐标系中,这支喷泉的函数关系式是( )
A.y=-+3B.y=3+1
C.y=-8+3
D.y=-8+3
9.抛物线y=x2-3x+的对称轴是( )
A.直线x=3 B.直线x=-3
C.直线x=6 D.直线x=-6
10.将二次函数y=-x2-4x+2化为y=a(x+m)2+k的形式,则( )
A.a=-1,m=-2,k=6
B.a=-1,m=2,k=6
C.a=1,m=-2,k=-6
D.a=-1,m=2,k=-6
11.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A.a>0,b<0,c>0
B.a<0,b<0,c>0
C.a<0,b>0,c<0
D.a<0,b>0,c>0
12.二次函数y=ax2+bx+a2-2(a,b为常数)的图象如图所示,则a的值为( )
A.-2 B.
C.1
D.±
13.如图,在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )
二.填空题
14.抛物线y=ax2与y=2x2形状相同,则a=________.
15.如图,四个函数图象对应的解析式分别是:①y=ax2,②y=bx2,③y=cx2,④y=dx2,则a,b,c,d的大小关系是_____________.
16.若抛物线y=x2+bx-c的图象经过点(1,2),则b-c的值为________.
17.抛物线y=-x2开口________,顶点坐标是________,当x________0时,y<0.
18.抛物线y=3(x+2)2可由抛物线y=3x2向______平移2个单位得到,它的顶点坐标为______________.
19.二次函数图象的顶点坐标为(2,1),它的形状与抛物线y=-2x2相同,则这个二次函数的解析式为__________________________________________.
20.将抛物线y=ax2+bx+c向左平移2个单位,再向下平移3个单位后得到抛物线y=2x2,则原抛物线是__________________________________________.
21.如图,由抛物线y=(x+2)2,y=(x+2)2+3和直线x=1,x=-2所围阴影部分的面积为________.
22.抛物线y=-2x2+bx+c的对称轴为直线x=1,则b=________.
23.抛物线y=x2-2x-8的对称轴为直线________,顶点坐标为________.
24.已知抛物线y=x2+2bx-4的顶点在y轴的右侧,则b的取值范围是________.
25.如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=-(x-6)2+4,则选取点B为坐标原点时的抛物线解析式是________________________________________________________________________.
26.已知抛物线y=x2+(m-2)x-2m,当m=________时,顶点在y轴上;当m=________时,顶点在x轴上;无论m取何值,抛物线必经过定点________.
三.解答题
27.已知抛物线y=ax2经过点(-2,-8).
(1)求此抛物线的解析式;
(2)判断点B(-1,-4)是否在此抛物线上;
(3)求出此抛物线上纵坐标为-4的点的坐标.
28.抛物线y=ax2(a≠0)与直线y=4x-3交于点A(m,1).
(1)求点A的坐标及抛物线的解析式;
(2)写出抛物线的开口方向、顶点坐标和对称轴;
(3)写出抛物线y=ax2与直线y=4x-3的另一个交点B的坐标.
29.某公园要建造一个圆形喷水池,在水池中央垂直于水面竖一根柱子,连喷头在内柱高为1m,水流在各个方向上沿形状相同的抛物线路径落下,如图1所示.根据设计图纸已知:在图2中,抛物线的最高点M距离柱子OA为1m,距离地面OB为1.8m.
(1)求图2中抛物线的解析式(不必求x的取值范围);
(2)如果不计其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
30.如图1是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如图2).
(1)求抛物线的解析式;
(2)求两盏景观灯之间的水平距离.
31.如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连结OA.
(1)求△OAB的面积;
(2)若抛物线y=-x2-2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).
1-5.BBCCA
6-10DACAB
10-13DBB
14.±2
15.a>b
>c>d
16.1
17.向下 (0,0)
≠
18.左 (-2,0)
19.y=-2(x-2)2+1或y=2(x-2)2+1
20.y=2(x-2)2+3(或y=2x2-8x+11)
21.9
22.4
23.x=1 (1,-9)
24.b<0
25.y=-(x+6)2+4
26.2 -2 (2,0) 【点拨】顶点在y轴上,可得对称轴直线x=-=0,即b=0,∴m=2时,顶点在y轴上;顶点在x轴上,可得顶点纵坐标y==0,即b2-4ac=0,∴m=-2时,顶点在x轴上;“无论m取何值,抛物线必经过定点”说明此点的坐标与m的取值无关,将原解析式变形为y=x2+(x-2)m-2x,令x=2,此时无论m取何值,得y=0,∴此定点为(2,0).
27.(1)y=-2x2; (2)点B(-1,-4)不在此抛物线上; (3)(,-4)或(-,-4).
28.(1)A(1,1),y=x2; (2)开口向上,顶点(0,0),对称轴为y轴;
(3)B(3,9).由得∴B(3,9).
29.(1)∵顶点为(1,1.8),∴设y=a(x-1)2+1.8,把A(0,1)代入得a=-,∴y=-(x-1)2+1.8; (2)当y=0时,-(x-1)2+1.8=0,x1=2.5,x2=-0.5(舍去),∴水池半径至少为2.5m.
30.(1)抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1),设抛物线的解析式是y=a(x-5)2+5,把(0,1)代入y=a(x-5)2+5得a=-,∴y=-(x-5)2+5(0≤x≤10); (2)由已知得两景观灯的纵坐标都是4,∴4=-(x-5)2+5,∴(x-5)2=1,∴x1=,x2=,∴两景观灯间的距离为-=5米.
31.(1)∵点A的坐标是(-2,4),AB⊥y轴,∴AB=2,OB=4,∴S△OAB=AB·OB=×2×4=4;
(2)①把点A的坐标(-2,4)代入y=-x2-2x+c,得-(-2)2-2×(-2)+c=4,∴c=4; ②∵y=-x2-2x+4=-(x+1)2+5,∴抛物线顶点D的坐标是(-1,5).∵OA的中点F的坐标是(-1,2),AB的中点E的坐标是(-1,4),∴m的取值范围为1
1.已知二次函数y=ax2的图象过点(-1,3),则a的值为( )
A.-3 B.3 C. D.-
2.若抛物线y=(2m-1)x2的开口向下,则m的取值范围是( )
A.m<0 B.m<
C.m> D.m>-
3.已知正方形的边长为x(cm),则它的面积y(cm2)与边长x(cm)的函数关系可表示为图中的( )
4.将函数y=kx2与y=kx+k的图象画在同一直角坐标系中,可能的是( )
5.抛物线y=(x+3)2+1的顶点坐标是( )
A.(-3,1) B.(-3,-1)
C.(3,-1) D.(3,1)
6.在同一坐标平面内,图象不可能由函数y=2x2+1的图象通过平移变换或轴对称变换得到的函数是( )
A.y=2(x+1)2-1 B.y=2x2+3
C.y=-2x2-1
D.y=x2-1
7.如图,在平面直角坐标系中,抛物线所表示的函数解析式为y=-2(x-h)2+k,则下列结论正确的是( )
A.h>0,k>0
B.h<0,k>0
C.h<0,k<0
D.h>0,k<0
8.某广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为1m的喷水管喷水最大高度为3m,此时喷水水平距离为m,在如图所示的坐标系中,这支喷泉的函数关系式是( )
A.y=-+3B.y=3+1
C.y=-8+3
D.y=-8+3
9.抛物线y=x2-3x+的对称轴是( )
A.直线x=3 B.直线x=-3
C.直线x=6 D.直线x=-6
10.将二次函数y=-x2-4x+2化为y=a(x+m)2+k的形式,则( )
A.a=-1,m=-2,k=6
B.a=-1,m=2,k=6
C.a=1,m=-2,k=-6
D.a=-1,m=2,k=-6
11.二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A.a>0,b<0,c>0
B.a<0,b<0,c>0
C.a<0,b>0,c<0
D.a<0,b>0,c>0
12.二次函数y=ax2+bx+a2-2(a,b为常数)的图象如图所示,则a的值为( )
A.-2 B.
C.1
D.±
13.如图,在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )
二.填空题
14.抛物线y=ax2与y=2x2形状相同,则a=________.
15.如图,四个函数图象对应的解析式分别是:①y=ax2,②y=bx2,③y=cx2,④y=dx2,则a,b,c,d的大小关系是_____________.
16.若抛物线y=x2+bx-c的图象经过点(1,2),则b-c的值为________.
17.抛物线y=-x2开口________,顶点坐标是________,当x________0时,y<0.
18.抛物线y=3(x+2)2可由抛物线y=3x2向______平移2个单位得到,它的顶点坐标为______________.
19.二次函数图象的顶点坐标为(2,1),它的形状与抛物线y=-2x2相同,则这个二次函数的解析式为__________________________________________.
20.将抛物线y=ax2+bx+c向左平移2个单位,再向下平移3个单位后得到抛物线y=2x2,则原抛物线是__________________________________________.
21.如图,由抛物线y=(x+2)2,y=(x+2)2+3和直线x=1,x=-2所围阴影部分的面积为________.
22.抛物线y=-2x2+bx+c的对称轴为直线x=1,则b=________.
23.抛物线y=x2-2x-8的对称轴为直线________,顶点坐标为________.
24.已知抛物线y=x2+2bx-4的顶点在y轴的右侧,则b的取值范围是________.
25.如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=-(x-6)2+4,则选取点B为坐标原点时的抛物线解析式是________________________________________________________________________.
26.已知抛物线y=x2+(m-2)x-2m,当m=________时,顶点在y轴上;当m=________时,顶点在x轴上;无论m取何值,抛物线必经过定点________.
三.解答题
27.已知抛物线y=ax2经过点(-2,-8).
(1)求此抛物线的解析式;
(2)判断点B(-1,-4)是否在此抛物线上;
(3)求出此抛物线上纵坐标为-4的点的坐标.
28.抛物线y=ax2(a≠0)与直线y=4x-3交于点A(m,1).
(1)求点A的坐标及抛物线的解析式;
(2)写出抛物线的开口方向、顶点坐标和对称轴;
(3)写出抛物线y=ax2与直线y=4x-3的另一个交点B的坐标.
29.某公园要建造一个圆形喷水池,在水池中央垂直于水面竖一根柱子,连喷头在内柱高为1m,水流在各个方向上沿形状相同的抛物线路径落下,如图1所示.根据设计图纸已知:在图2中,抛物线的最高点M距离柱子OA为1m,距离地面OB为1.8m.
(1)求图2中抛物线的解析式(不必求x的取值范围);
(2)如果不计其他因素,那么水池的半径至少为多少时,才能使喷出的水流都落在水池内?
30.如图1是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的截面图放在平面直角坐标系中(如图2).
(1)求抛物线的解析式;
(2)求两盏景观灯之间的水平距离.
31.如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连结OA.
(1)求△OAB的面积;
(2)若抛物线y=-x2-2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).
1-5.BBCCA
6-10DACAB
10-13DBB
14.±2
15.a>b
>c>d
16.1
17.向下 (0,0)
≠
18.左 (-2,0)
19.y=-2(x-2)2+1或y=2(x-2)2+1
20.y=2(x-2)2+3(或y=2x2-8x+11)
21.9
22.4
23.x=1 (1,-9)
24.b<0
25.y=-(x+6)2+4
26.2 -2 (2,0) 【点拨】顶点在y轴上,可得对称轴直线x=-=0,即b=0,∴m=2时,顶点在y轴上;顶点在x轴上,可得顶点纵坐标y==0,即b2-4ac=0,∴m=-2时,顶点在x轴上;“无论m取何值,抛物线必经过定点”说明此点的坐标与m的取值无关,将原解析式变形为y=x2+(x-2)m-2x,令x=2,此时无论m取何值,得y=0,∴此定点为(2,0).
27.(1)y=-2x2; (2)点B(-1,-4)不在此抛物线上; (3)(,-4)或(-,-4).
28.(1)A(1,1),y=x2; (2)开口向上,顶点(0,0),对称轴为y轴;
(3)B(3,9).由得∴B(3,9).
29.(1)∵顶点为(1,1.8),∴设y=a(x-1)2+1.8,把A(0,1)代入得a=-,∴y=-(x-1)2+1.8; (2)当y=0时,-(x-1)2+1.8=0,x1=2.5,x2=-0.5(舍去),∴水池半径至少为2.5m.
30.(1)抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1),设抛物线的解析式是y=a(x-5)2+5,把(0,1)代入y=a(x-5)2+5得a=-,∴y=-(x-5)2+5(0≤x≤10); (2)由已知得两景观灯的纵坐标都是4,∴4=-(x-5)2+5,∴(x-5)2=1,∴x1=,x2=,∴两景观灯间的距离为-=5米.
31.(1)∵点A的坐标是(-2,4),AB⊥y轴,∴AB=2,OB=4,∴S△OAB=AB·OB=×2×4=4;
(2)①把点A的坐标(-2,4)代入y=-x2-2x+c,得-(-2)2-2×(-2)+c=4,∴c=4; ②∵y=-x2-2x+4=-(x+1)2+5,∴抛物线顶点D的坐标是(-1,5).∵OA的中点F的坐标是(-1,2),AB的中点E的坐标是(-1,4),∴m的取值范围为1
同课章节目录
