2.4 等腰三角形的判定定理课时达标检测(含解析)
文档属性
| 名称 | 2.4 等腰三角形的判定定理课时达标检测(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 11:41:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2021年八年级上册数学同步练习卷
2.4 等腰三角形的判定定理
一、单选题
1.在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50 B.∠A=40°,∠B=60°
C.∠A=40°,∠B=70 D.∠A=40°,∠B=80°
2.已知下列各组数据,能构成等腰三角形三边边长的是( )
A.2 , 2 , 1 B.1 , 2 , 1 C.1 , 3 , 1 D.2 , 2 , 5
3.下列两个三角形中,一定全等的是( )
A.有一个角是 40°,腰相等的两个等腰三角形
B.两个等边三角形
C.有一个角是 100°,底相等的两个等腰三角形
D.有一条边相等,有一个内角相等的两个等腰三角形
4.如图,是等边三角形,D,E,F为各边中点,则图中的等边三角形有( )
A.2个 B.3个 C.4个 D.5个
5.如图,△ABC是等边三角形,DE∥BC,若AB=10,BD=6,则△ADE的周长为( )
A.4 B.30 C.18 D.12
6.若△ABC三条边的长度分别为m,n,p,且,则这个三角形为
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
7.已知等腰三角形的一边长为6,一个内角为60°,则它的周长是( )
A.12 B.15 C.18 D.20
8.△ABC中AB=AC,∠A=36°,BD平分∠ABC交AC于D,则图中的等腰三角形有( )
A.1个 B.2个 C.3个 D.4个
9.在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )
A.4个 B.3个 C.2个 D.1个
10.如图,等腰中,分别为上的点,且,则的度数为( )
A. B. C. D.
11.如图,AB=AC,∠A=36°,AB的垂直平分线交AC于点D,有下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ABD是等腰三角形;④△BCD是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如下图,△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是( )
A.8+2a B.8+a C.6+a D.6+2a
二、填空题
13.等腰三角形的一个内角是,则它的顶角度数是_______________.
14.在△ABC中,∠A=40°,∠C=70°,则△ABC是______________三角形.
15.已知:如图所示,点在的延长线上,,则的形状为___________
16.在△ABC中,高AD和BE所在直线交于点H,且BH=AC,则∠ABC=____.
17.如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是 ______cm.
18.如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为__.
三、解答题
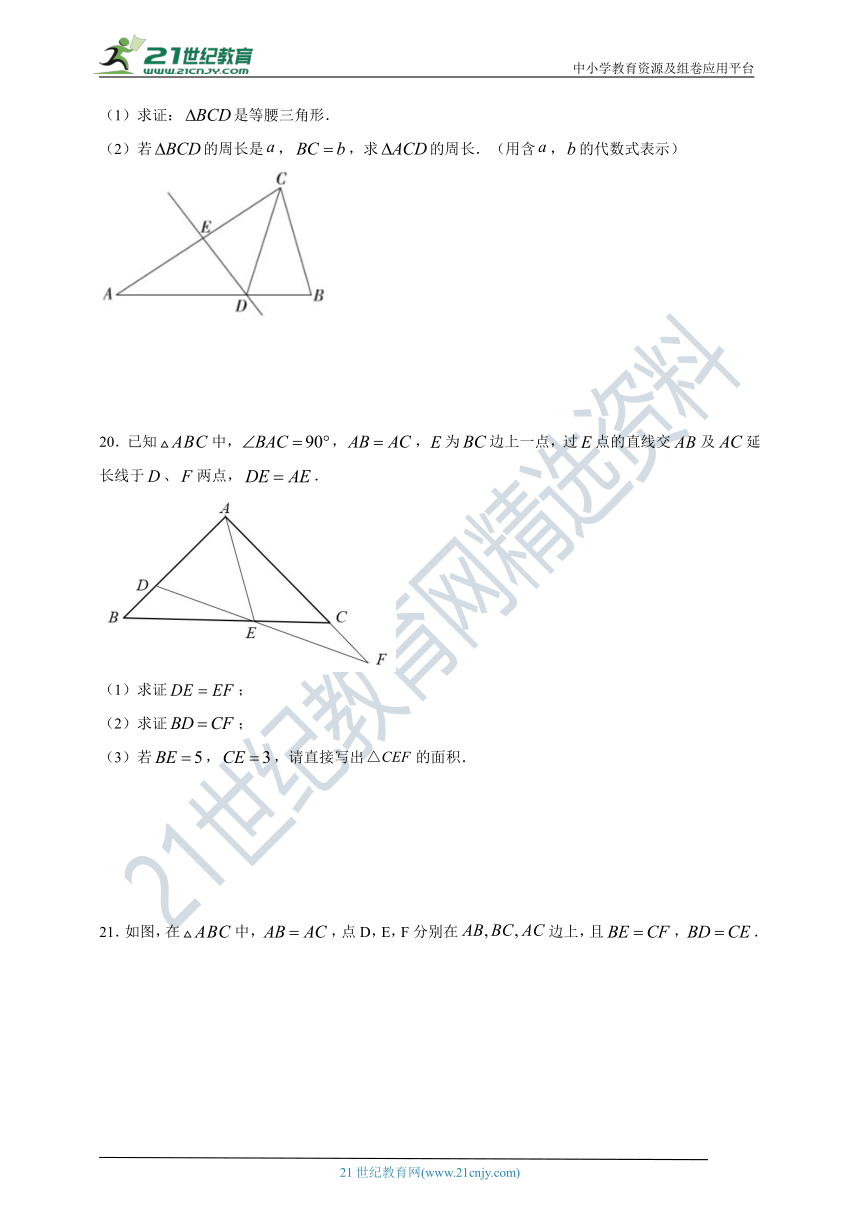
19.如图,在中,,,是的垂直平分线.
(1)求证:是等腰三角形.
(2)若的周长是,,求的周长.(用含,的代数式表示)
20.已知中,,,为边上一点,过点的直线交及延长线于、两点,.
(1)求证;
(2)求证;
(3)若,,请直接写出的面积.
21.如图,在中,,点D,E,F分别在边上,且,.
(1)求证:是等腰三角形;
(2)求证:;
(3)当时,求的度数.
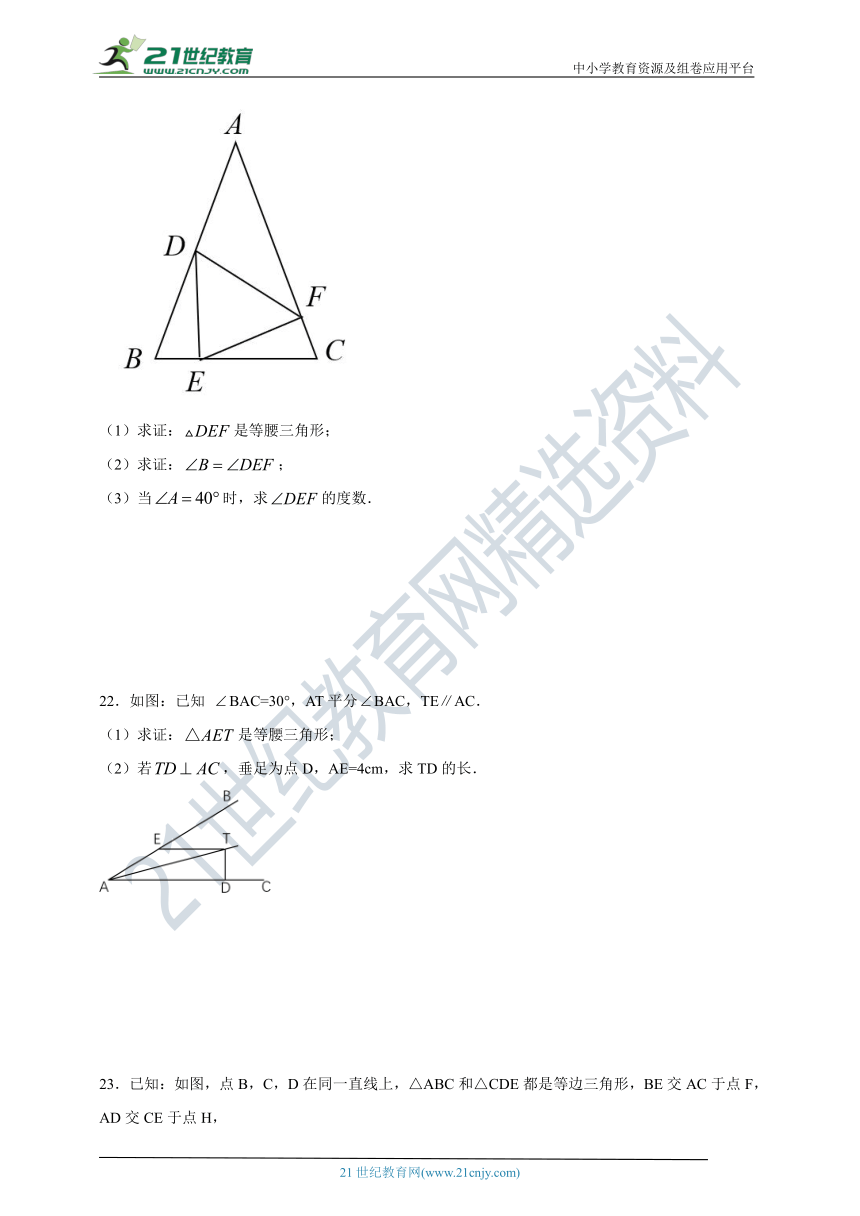
22.如图:已知 BAC=30°,AT平分BAC,TE∥AC.
(1)求证:是等腰三角形;
(2)若,垂足为点D,AE=4cm,求TD的长.
23.已知:如图,点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
(1)求证:△BCE≌△ACD;
(2)求证:CF=CH;
(3)判断△CFH的形状并说明理由.
参考答案
1.C
【详解】
当顶角为∠A=40°时,∠C=70°≠∠B,当顶角为∠B=50°时,∠C=65°≠∠A,故A项错误;当顶角为∠A=40°时,∠C=70°≠∠B,当顶角为∠B=60°时,∠C=60°≠∠A,故B选项错误;当顶角为∠A=40°时,∠C=70°=∠B,故C选项正确;当顶角为∠A=40°时,∠C=70°≠∠B,当顶角为∠B=80°时,∠C=50°≠∠A,故D项错误.因此选C.
2.A
【详解】
解:A选项:2+1>2,能构成三角形,且有两边相等,故是正确的;
B选项:1+1=2,不能构成三角形,故是错误的;
C选项:1+1<3,不能构成三角形,故是错误的;
D选项:2+2<5,不能构成三角形,故是错误的;
3.C
【详解】
解:A、不正确,没有指明该角是顶角还是底角;
B、不正确,虽然其角相等,但边不一定相等; SAS;
C、正确,分析得该角不顶角,符合判定
D、不正确,没有指明边与角具体是腰还是底边,是顶角还是底角.
4.D
【详解】
∵为等边三角形,
∴.
∵D,E,F为各边中点,
∴,
∴为等边三角形,
∴,
∴为等边三角形,
∴题图中的等边三角形共有5个.
5.D
【详解】
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∵DE∥BC,
∴∠ADE=∠AED=∠B=∠C=60°,
∴△ADE为等边三角形,
∵AB=10,BD=6,
∴AD=AB﹣BD=10﹣6=4,
∴△ADE的周长为12.
6.B
【详解】
∵|m-n|+(n-p)2=0,
∴|m-n|=0,(n-p)2=0,
∴m=n,n=p,
∴m=n=p,
∴△ABC为等边三角形.
7.C
【详解】
解:∵等腰三角形的一个内角为60°,
∴此等腰三角形是等边三角形.
∵一边长为6,
∴它的周长为18.
8.C
【解析】
试题分析:∵AB=AC,
∴△ABC是等腰三角形.
∵∠A=36°,
∴∠C=∠ABC=72°.
BD平分∠ABC交AC于D,
∴∠ABD=∠DBC=36°,
∵∠A=∠ABD=36°,
∴△ABD是等腰三角形.
∠BDC=∠A+∠ABD=36°+36°=72°=∠C,
∴△BDC是等腰三角形.
∴共有3个等腰三角形.
9.C
【详解】
解:①因为外角和与其对应的内角的和是180°,已知有一个外角是120°,即是有一个内角是60°,有一个内角为60°的等腰三角形是等边三角形.该结论正确;
②两个外角相等说明该三角形中两个内角相等,而等腰三角形的两个底角是相等的,故不能确定该三角形是等边三角形.该结论错误;
③等腰三角形的底边上的高和中线本来就是重合的,“有一边”可能是底边,故不能保证该三角形是等边三角形.该结论错误;
④三个外角都相等的三角形是等边三角形,说法正确,
正确的命题有2个,
10.A
【详解】
如图,在上取点D,使,连接.设,则.
,
.
又,
,
,
,
,
为等边三角形,
,
,,
,
.
11.D
【解析】
已知∠A=36°,AB=AC,根据等腰三角形的性质和三角形的内角和定理可得∠ABC=∠C=72°,①正确;由DM是AB的垂直平分线,可得DA=DB,所以∠DBA=∠A=36°,即可得∠DBC=∠ABC-∠DBA=36°,所以BD是∠ABC的平分线,②正确;由②的过程可知:△ABD是等腰三角形,△BCD是等腰三角形,③④都正确,所以①②③④正确,共4个.故选D.
12.D
【解析】
试题分析:由∠P=60°,MN=NP,可得△MNP是等边三角形,再根据等边三角形的“三线合一”的性质以及等腰三角形的判定,即可求得结果.
∵∠P=60°,MN=NP
∴△MNP是等边三角形.
又∵MQ⊥PN,垂足为Q,
∴PM=PN=MN=4,NQ=NG=2,MQ=a,∠QMN=30°,∠PNM=60°,
∵NG=NQ,
∴∠G=∠QMN,
∴QG=MQ=a,
∵△MNP的周长为12,
∴MN=4,NG=2,
∴△MGQ周长是6+2a.
故选D.
13.20度或80度
【详解】
当80°是等腰三角形的顶角时,则顶角就是80°;
当80°是等腰三角形的底角时,则顶角是180°?80°×2=20°.
故答案为:80°或20°.
14.等腰
【详解】
解:∵在△ABC中,∠A=40°,∠C=70°,
∴∠B=180°-∠A-∠C=70°
∴∠B=∠C
∴△ABC为等腰三角形
15.等边三角形
【详解】
解:∵点在的延长线上,,
∴,
∵,
∴△ABC的形状为等边三角形.
故答案为:等边三角形.
16.45°或135°
【详解】
解:分为三种情况:
①如图1,
、是的高,
,,
,,
,
在和中
,
,
,
,
,
②如图2,
,,
,
,
,
在和中,
,
,
,
,
,
,
;
③高和所在的直线交于点,
,
,,
,
在和中
,
,
,
,
17.8.
【详解】
解:延长DE交BC于M,延长AE交BC于N,作EF∥BC于F,
∵AB=AC,AE平分∠BAC,
∴AN⊥BC,BN=CN,
∵∠DBC=∠D=60°,
∴△BDM为等边三角形,
∴△EFD为等边三角形,
∵BD=5,DE=3,
∴EM=2,
∵△BDM为等边三角形,
∴∠DMB=60°,
∵AN⊥BC,
∴∠ENM=90°,
∴∠NEM=30°,
∴NM=1,
∴BN=4,
∴BC=2BN=8(cm),
故答案为8.
18.6
【详解】
解:
在AD上截取AF=AE,连接BF,如图所示:
AB=AC,∠FAB=∠EAC,
,
BF=EC,∠BFA=∠E,
∠D+∠E=180°,∠BFA+∠DFB=180°,
∠DFB=∠D,
BF=BD,
BD=6,
CE=6.
19.(1)详见解析;(2)a+b
【详解】
(1)∵,
∴
∵是的垂直平分线
∴
∴
∵是的外角
∴
∴
∴
∴是等腰三角形;
(2)∵,的周长是
∴
∵
∴
∴的周长.
20.(1)证明见解析;(2)证明见解析;(3)
【详解】
证明:(1)
(2)如图,过作交于,
,,
,
,
,
,
在与中,
(3)过作于,
,
,
,
,
,
,
,
,
21.(1)证明见解析;(2)证明见解析;(3)70°
【详解】
(1)∵,
∴,
在和中
∴,
∴,
∴是等腰三角形;
(2)∵,
∴,
∴;
(3)由(2)知,
∵,
∴.
22.(1)见解析;(2)2cm
【详解】
解:(1)∵AT平分BAC.
∴∠EAT=∠TAD.
∵TE∥AC.
∴∠TAD=∠ETA.
∴∠EAT=∠ETA.
∴是等腰三角形.
(2)过点T作TFAB,垂足点F,
∵AT平分BAC,TFAB,.
∴据角平分线定理可得DT=TF.
∵在RT△TFE中,ET=4cm,∠FET=30°,则TF=2cm,
∴TD=2cm.
23.(1)证明见解析;(2)证明见解析;(3)△CFH是等边三角形,理由见解析.
【详解】
解:(1)∵∠BCA=∠DCE=60°,
∴∠BCE=∠ACD.
又BC=AC、CE=CD,
∴△BCE≌△ACD.
(2)∵△BCE≌△ACD,
∴∠CBF=∠CAH.
∵∠ACB=∠DCE=60°,
∴∠ACH=60°.
∴∠BCF=∠ACH.
又BC=AC,
∴△BCF≌△ACH.
∴CF=CH.
(3)∵CF=CH,∠ACH=60°,
∴△CFH是等边三角形.
_21?????????è?????(www.21cnjy.com)_
浙教版2021年八年级上册数学同步练习卷
2.4 等腰三角形的判定定理
一、单选题
1.在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50 B.∠A=40°,∠B=60°
C.∠A=40°,∠B=70 D.∠A=40°,∠B=80°
2.已知下列各组数据,能构成等腰三角形三边边长的是( )
A.2 , 2 , 1 B.1 , 2 , 1 C.1 , 3 , 1 D.2 , 2 , 5
3.下列两个三角形中,一定全等的是( )
A.有一个角是 40°,腰相等的两个等腰三角形
B.两个等边三角形
C.有一个角是 100°,底相等的两个等腰三角形
D.有一条边相等,有一个内角相等的两个等腰三角形
4.如图,是等边三角形,D,E,F为各边中点,则图中的等边三角形有( )
A.2个 B.3个 C.4个 D.5个
5.如图,△ABC是等边三角形,DE∥BC,若AB=10,BD=6,则△ADE的周长为( )
A.4 B.30 C.18 D.12
6.若△ABC三条边的长度分别为m,n,p,且,则这个三角形为
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
7.已知等腰三角形的一边长为6,一个内角为60°,则它的周长是( )
A.12 B.15 C.18 D.20
8.△ABC中AB=AC,∠A=36°,BD平分∠ABC交AC于D,则图中的等腰三角形有( )
A.1个 B.2个 C.3个 D.4个
9.在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )
A.4个 B.3个 C.2个 D.1个
10.如图,等腰中,分别为上的点,且,则的度数为( )
A. B. C. D.
11.如图,AB=AC,∠A=36°,AB的垂直平分线交AC于点D,有下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ABD是等腰三角形;④△BCD是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如下图,△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是( )
A.8+2a B.8+a C.6+a D.6+2a
二、填空题
13.等腰三角形的一个内角是,则它的顶角度数是_______________.
14.在△ABC中,∠A=40°,∠C=70°,则△ABC是______________三角形.
15.已知:如图所示,点在的延长线上,,则的形状为___________
16.在△ABC中,高AD和BE所在直线交于点H,且BH=AC,则∠ABC=____.
17.如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是 ______cm.
18.如图,△ABC中,AB=AC,D、E分别在CA、BA的延长线上,连接BD、CE,且∠D+∠E=180°,若BD=6,则CE的长为__.
三、解答题
19.如图,在中,,,是的垂直平分线.
(1)求证:是等腰三角形.
(2)若的周长是,,求的周长.(用含,的代数式表示)
20.已知中,,,为边上一点,过点的直线交及延长线于、两点,.
(1)求证;
(2)求证;
(3)若,,请直接写出的面积.
21.如图,在中,,点D,E,F分别在边上,且,.
(1)求证:是等腰三角形;
(2)求证:;
(3)当时,求的度数.
22.如图:已知 BAC=30°,AT平分BAC,TE∥AC.
(1)求证:是等腰三角形;
(2)若,垂足为点D,AE=4cm,求TD的长.
23.已知:如图,点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
(1)求证:△BCE≌△ACD;
(2)求证:CF=CH;
(3)判断△CFH的形状并说明理由.
参考答案
1.C
【详解】
当顶角为∠A=40°时,∠C=70°≠∠B,当顶角为∠B=50°时,∠C=65°≠∠A,故A项错误;当顶角为∠A=40°时,∠C=70°≠∠B,当顶角为∠B=60°时,∠C=60°≠∠A,故B选项错误;当顶角为∠A=40°时,∠C=70°=∠B,故C选项正确;当顶角为∠A=40°时,∠C=70°≠∠B,当顶角为∠B=80°时,∠C=50°≠∠A,故D项错误.因此选C.
2.A
【详解】
解:A选项:2+1>2,能构成三角形,且有两边相等,故是正确的;
B选项:1+1=2,不能构成三角形,故是错误的;
C选项:1+1<3,不能构成三角形,故是错误的;
D选项:2+2<5,不能构成三角形,故是错误的;
3.C
【详解】
解:A、不正确,没有指明该角是顶角还是底角;
B、不正确,虽然其角相等,但边不一定相等; SAS;
C、正确,分析得该角不顶角,符合判定
D、不正确,没有指明边与角具体是腰还是底边,是顶角还是底角.
4.D
【详解】
∵为等边三角形,
∴.
∵D,E,F为各边中点,
∴,
∴为等边三角形,
∴,
∴为等边三角形,
∴题图中的等边三角形共有5个.
5.D
【详解】
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,
∵DE∥BC,
∴∠ADE=∠AED=∠B=∠C=60°,
∴△ADE为等边三角形,
∵AB=10,BD=6,
∴AD=AB﹣BD=10﹣6=4,
∴△ADE的周长为12.
6.B
【详解】
∵|m-n|+(n-p)2=0,
∴|m-n|=0,(n-p)2=0,
∴m=n,n=p,
∴m=n=p,
∴△ABC为等边三角形.
7.C
【详解】
解:∵等腰三角形的一个内角为60°,
∴此等腰三角形是等边三角形.
∵一边长为6,
∴它的周长为18.
8.C
【解析】
试题分析:∵AB=AC,
∴△ABC是等腰三角形.
∵∠A=36°,
∴∠C=∠ABC=72°.
BD平分∠ABC交AC于D,
∴∠ABD=∠DBC=36°,
∵∠A=∠ABD=36°,
∴△ABD是等腰三角形.
∠BDC=∠A+∠ABD=36°+36°=72°=∠C,
∴△BDC是等腰三角形.
∴共有3个等腰三角形.
9.C
【详解】
解:①因为外角和与其对应的内角的和是180°,已知有一个外角是120°,即是有一个内角是60°,有一个内角为60°的等腰三角形是等边三角形.该结论正确;
②两个外角相等说明该三角形中两个内角相等,而等腰三角形的两个底角是相等的,故不能确定该三角形是等边三角形.该结论错误;
③等腰三角形的底边上的高和中线本来就是重合的,“有一边”可能是底边,故不能保证该三角形是等边三角形.该结论错误;
④三个外角都相等的三角形是等边三角形,说法正确,
正确的命题有2个,
10.A
【详解】
如图,在上取点D,使,连接.设,则.
,
.
又,
,
,
,
,
为等边三角形,
,
,,
,
.
11.D
【解析】
已知∠A=36°,AB=AC,根据等腰三角形的性质和三角形的内角和定理可得∠ABC=∠C=72°,①正确;由DM是AB的垂直平分线,可得DA=DB,所以∠DBA=∠A=36°,即可得∠DBC=∠ABC-∠DBA=36°,所以BD是∠ABC的平分线,②正确;由②的过程可知:△ABD是等腰三角形,△BCD是等腰三角形,③④都正确,所以①②③④正确,共4个.故选D.
12.D
【解析】
试题分析:由∠P=60°,MN=NP,可得△MNP是等边三角形,再根据等边三角形的“三线合一”的性质以及等腰三角形的判定,即可求得结果.
∵∠P=60°,MN=NP
∴△MNP是等边三角形.
又∵MQ⊥PN,垂足为Q,
∴PM=PN=MN=4,NQ=NG=2,MQ=a,∠QMN=30°,∠PNM=60°,
∵NG=NQ,
∴∠G=∠QMN,
∴QG=MQ=a,
∵△MNP的周长为12,
∴MN=4,NG=2,
∴△MGQ周长是6+2a.
故选D.
13.20度或80度
【详解】
当80°是等腰三角形的顶角时,则顶角就是80°;
当80°是等腰三角形的底角时,则顶角是180°?80°×2=20°.
故答案为:80°或20°.
14.等腰
【详解】
解:∵在△ABC中,∠A=40°,∠C=70°,
∴∠B=180°-∠A-∠C=70°
∴∠B=∠C
∴△ABC为等腰三角形
15.等边三角形
【详解】
解:∵点在的延长线上,,
∴,
∵,
∴△ABC的形状为等边三角形.
故答案为:等边三角形.
16.45°或135°
【详解】
解:分为三种情况:
①如图1,
、是的高,
,,
,,
,
在和中
,
,
,
,
,
②如图2,
,,
,
,
,
在和中,
,
,
,
,
,
,
;
③高和所在的直线交于点,
,
,,
,
在和中
,
,
,
,
17.8.
【详解】
解:延长DE交BC于M,延长AE交BC于N,作EF∥BC于F,
∵AB=AC,AE平分∠BAC,
∴AN⊥BC,BN=CN,
∵∠DBC=∠D=60°,
∴△BDM为等边三角形,
∴△EFD为等边三角形,
∵BD=5,DE=3,
∴EM=2,
∵△BDM为等边三角形,
∴∠DMB=60°,
∵AN⊥BC,
∴∠ENM=90°,
∴∠NEM=30°,
∴NM=1,
∴BN=4,
∴BC=2BN=8(cm),
故答案为8.
18.6
【详解】
解:
在AD上截取AF=AE,连接BF,如图所示:
AB=AC,∠FAB=∠EAC,
,
BF=EC,∠BFA=∠E,
∠D+∠E=180°,∠BFA+∠DFB=180°,
∠DFB=∠D,
BF=BD,
BD=6,
CE=6.
19.(1)详见解析;(2)a+b
【详解】
(1)∵,
∴
∵是的垂直平分线
∴
∴
∵是的外角
∴
∴
∴
∴是等腰三角形;
(2)∵,的周长是
∴
∵
∴
∴的周长.
20.(1)证明见解析;(2)证明见解析;(3)
【详解】
证明:(1)
(2)如图,过作交于,
,,
,
,
,
,
在与中,
(3)过作于,
,
,
,
,
,
,
,
,
21.(1)证明见解析;(2)证明见解析;(3)70°
【详解】
(1)∵,
∴,
在和中
∴,
∴,
∴是等腰三角形;
(2)∵,
∴,
∴;
(3)由(2)知,
∵,
∴.
22.(1)见解析;(2)2cm
【详解】
解:(1)∵AT平分BAC.
∴∠EAT=∠TAD.
∵TE∥AC.
∴∠TAD=∠ETA.
∴∠EAT=∠ETA.
∴是等腰三角形.
(2)过点T作TFAB,垂足点F,
∵AT平分BAC,TFAB,.
∴据角平分线定理可得DT=TF.
∵在RT△TFE中,ET=4cm,∠FET=30°,则TF=2cm,
∴TD=2cm.
23.(1)证明见解析;(2)证明见解析;(3)△CFH是等边三角形,理由见解析.
【详解】
解:(1)∵∠BCA=∠DCE=60°,
∴∠BCE=∠ACD.
又BC=AC、CE=CD,
∴△BCE≌△ACD.
(2)∵△BCE≌△ACD,
∴∠CBF=∠CAH.
∵∠ACB=∠DCE=60°,
∴∠ACH=60°.
∴∠BCF=∠ACH.
又BC=AC,
∴△BCF≌△ACH.
∴CF=CH.
(3)∵CF=CH,∠ACH=60°,
∴△CFH是等边三角形.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
