高中信息技术浙教版(2019)必修1 第二章2.2算法结构 算法解决问题 课件(16张)
文档属性
| 名称 | 高中信息技术浙教版(2019)必修1 第二章2.2算法结构 算法解决问题 课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 798.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览



文档简介
算法控制结构
算法解决问题
上节回顾
1.算法的概念
解决问题或完成任务的一系列步骤
为了解决问题而需要让计算机有序执行的、无歧义的、有限步骤的集合
2.算法的特征
有穷性;可行性;确定性;0个或多个输入;1个或多个输出;
3.算法的要素
数据,运算,控制转移
4.算法的描述
自然语言、流程图、伪代码、计算机程序设计语言
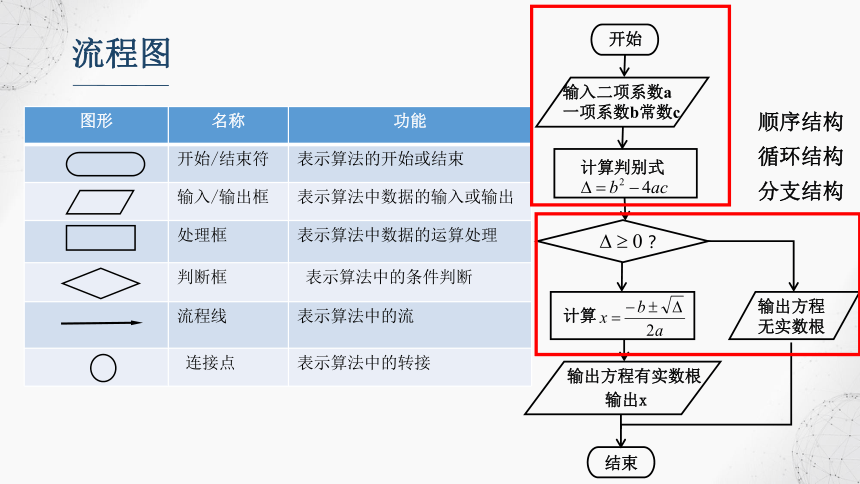
流程图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形
名称
功能
开始/结束符
表示算法的开始或结束
输入/输出框
表示算法中数据的输入或输出
处理框
表示算法中数据的运算处理
判断框
表示算法中的条件判断
流程线
表示算法中的流
连接点
表示算法中的转接
开始
输入二项系数a
一项系数b常数c
计算判别式
?
计算
输出方程
无实数根
输出方程有实数根
输出x
结束
顺序结构
分支结构
循环结构
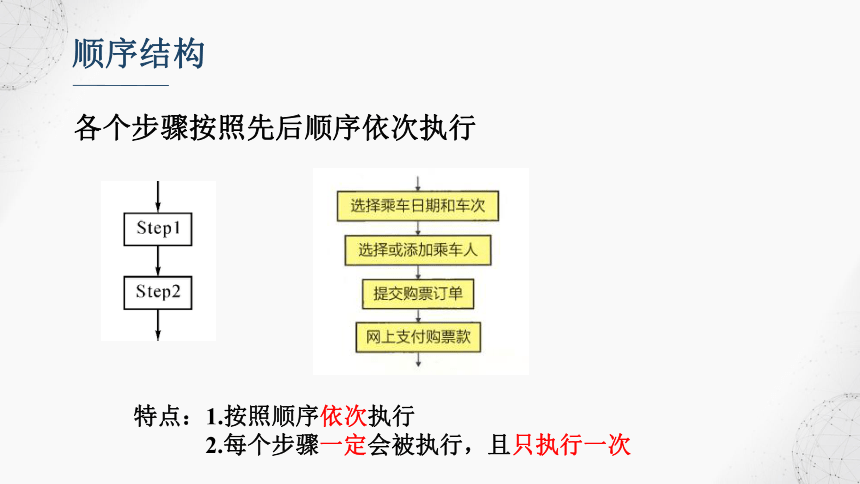
顺序结构
各个步骤按照先后顺序依次执行
特点:1.按照顺序依次执行
2.每个步骤一定会被执行,且只执行一次
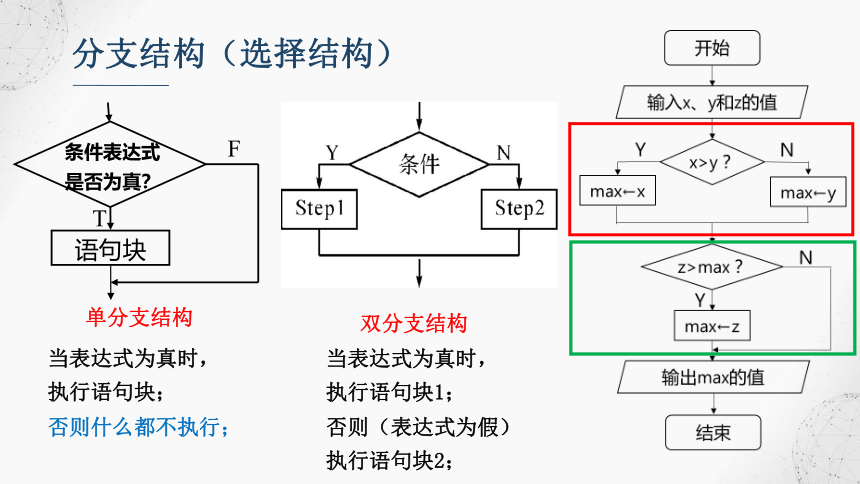
分支结构(选择结构)
根据条件判断选择不同的分支执行:
条件为真时执行Y指向的语句,否则执行N指向的语句。
选择结构中,必有一个分支被执行,其余分支不执行。
分支结构(选择结构)
语句块
T
F
条件表达式是否为真?
当表达式为真时,
执行语句块;
否则什么都不执行;
当表达式为真时,
执行语句块1;
否则(表达式为假)
执行语句块2;
单分支结构
双分支结构
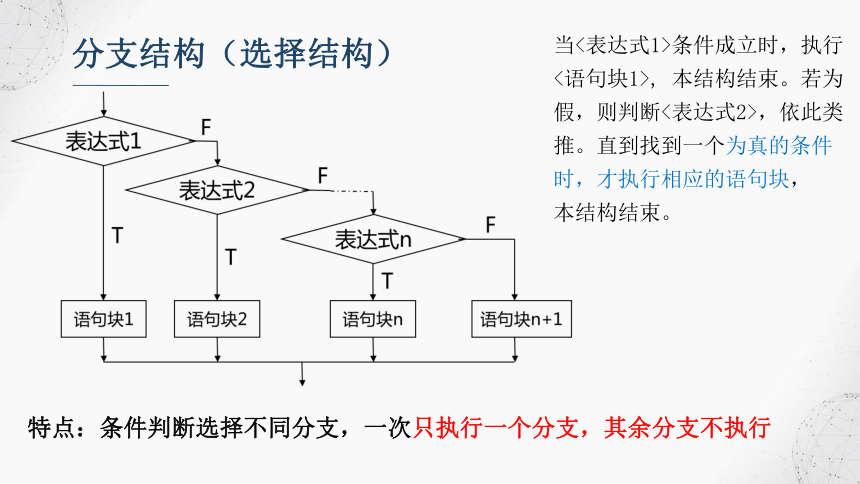
分支结构(选择结构)
特点:条件判断选择不同分支,一次只执行一个分支,其余分支不执行
当<表达式1>条件成立时,执行<语句块1>, 本结构结束。若为假,则判断<表达式2>,依此类推。直到找到一个为真的条件时,才执行相应的语句块,
本结构结束。
循环结构
对某个条件进行判断,当符合条件时,执行Y指向的语句(循环体),然后返回重新判断这个条件,当符合条件时,再次执行循环体。重复上述过程,直到不符合条件,则跳出循环,执行循环体后面的指令。
若循环条件始终满足?
算法无限循环,违背有穷性
分支or循环
判断依据:分支结构:条件是否成立只判断1次
循环结构:条件是否成立往往判断多次
分支结构
循环结构
分支结构
循环结构
累加器
False
True
i=i+2
i>0?
开始
s←0, i←100
s←s+i
输出n
结束
如图所示,该流程图所表示的算法违背了算法的
有穷性,下列修改方法中,可以改正错误的是( )
A.1处改为i←1
B.2处改为s>=0?
C.3处改为i←i-2
D.1处改为s←s-i
1
2
3
C
累加器 :s←s+i
计数器
s←0,n←0
x<0?
Y
s←s+x,n←n+1
N
开始
输入x
输出n
结束
依次输入x的值为 3 、2 、1、-1
n=1
n=2
n=3
i←1
c=0
i<=10?
Y
i←i+1
N
输出c
i能被3整除?
Y
c←c+1
N
计数器:n←n+1
100?
c=c+1
统计10以内能被3整除的个数
用算法解决问题
用算法求解圆的面积,已知圆的半径r,圆的面积s
明确要素:
r s
明确数学函数:
具体算法设计:
1.输入半径r
2.s←
3.输出面积s
描述算法:
输入r
s←
输出s
用算法解决问题
1.抽象与建模
a.提炼核心要素并加以确定或假设
b.用数学符号描述解决问题的计算模型
2.设计算法
a.输入数据
b.处理数据
c.输出处理结果
3.描述算法
自然语言、流程图、伪代码、计算机程序设计语言
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
用算法解决问题
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
明确要素:
明确数学函数:
具体算法设计:
描述算法:
里程数x 费用f
1.输入里程数x
2.若0 若3 若x>=10,f=10+7*2+3(x-10)
3.输出费用f
用算法解决问题
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
x<=3?
Y
f=10
N
开始
输入里程数x
输出费用f
结束
f=10+2(x-3)
x<=10?
f=10+2*7+3(x-10)
Y
N
判定一个正整数a是否是素数
a>2?
Y
N
开始
输入a
结束
iY
N
i=2
输出a不符合要求
a % i =0
输出a是素数
输出a不是素数
i=i+1
2~a-1都无法被a整除
算法解决问题
上节回顾
1.算法的概念
解决问题或完成任务的一系列步骤
为了解决问题而需要让计算机有序执行的、无歧义的、有限步骤的集合
2.算法的特征
有穷性;可行性;确定性;0个或多个输入;1个或多个输出;
3.算法的要素
数据,运算,控制转移
4.算法的描述
自然语言、流程图、伪代码、计算机程序设计语言
流程图
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形
名称
功能
开始/结束符
表示算法的开始或结束
输入/输出框
表示算法中数据的输入或输出
处理框
表示算法中数据的运算处理
判断框
表示算法中的条件判断
流程线
表示算法中的流
连接点
表示算法中的转接
开始
输入二项系数a
一项系数b常数c
计算判别式
?
计算
输出方程
无实数根
输出方程有实数根
输出x
结束
顺序结构
分支结构
循环结构
顺序结构
各个步骤按照先后顺序依次执行
特点:1.按照顺序依次执行
2.每个步骤一定会被执行,且只执行一次
分支结构(选择结构)
根据条件判断选择不同的分支执行:
条件为真时执行Y指向的语句,否则执行N指向的语句。
选择结构中,必有一个分支被执行,其余分支不执行。
分支结构(选择结构)
语句块
T
F
条件表达式是否为真?
当表达式为真时,
执行语句块;
否则什么都不执行;
当表达式为真时,
执行语句块1;
否则(表达式为假)
执行语句块2;
单分支结构
双分支结构
分支结构(选择结构)
特点:条件判断选择不同分支,一次只执行一个分支,其余分支不执行
当<表达式1>条件成立时,执行<语句块1>, 本结构结束。若为假,则判断<表达式2>,依此类推。直到找到一个为真的条件时,才执行相应的语句块,
本结构结束。
循环结构
对某个条件进行判断,当符合条件时,执行Y指向的语句(循环体),然后返回重新判断这个条件,当符合条件时,再次执行循环体。重复上述过程,直到不符合条件,则跳出循环,执行循环体后面的指令。
若循环条件始终满足?
算法无限循环,违背有穷性
分支or循环
判断依据:分支结构:条件是否成立只判断1次
循环结构:条件是否成立往往判断多次
分支结构
循环结构
分支结构
循环结构
累加器
False
True
i=i+2
i>0?
开始
s←0, i←100
s←s+i
输出n
结束
如图所示,该流程图所表示的算法违背了算法的
有穷性,下列修改方法中,可以改正错误的是( )
A.1处改为i←1
B.2处改为s>=0?
C.3处改为i←i-2
D.1处改为s←s-i
1
2
3
C
累加器 :s←s+i
计数器
s←0,n←0
x<0?
Y
s←s+x,n←n+1
N
开始
输入x
输出n
结束
依次输入x的值为 3 、2 、1、-1
n=1
n=2
n=3
i←1
c=0
i<=10?
Y
i←i+1
N
输出c
i能被3整除?
Y
c←c+1
N
计数器:n←n+1
100?
c=c+1
统计10以内能被3整除的个数
用算法解决问题
用算法求解圆的面积,已知圆的半径r,圆的面积s
明确要素:
r s
明确数学函数:
具体算法设计:
1.输入半径r
2.s←
3.输出面积s
描述算法:
输入r
s←
输出s
用算法解决问题
1.抽象与建模
a.提炼核心要素并加以确定或假设
b.用数学符号描述解决问题的计算模型
2.设计算法
a.输入数据
b.处理数据
c.输出处理结果
3.描述算法
自然语言、流程图、伪代码、计算机程序设计语言
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
用算法解决问题
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
明确要素:
明确数学函数:
具体算法设计:
描述算法:
里程数x 费用f
1.输入里程数x
2.若0
3.输出费用f
用算法解决问题
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
x<=3?
Y
f=10
N
开始
输入里程数x
输出费用f
结束
f=10+2(x-3)
x<=10?
f=10+2*7+3(x-10)
Y
N
判定一个正整数a是否是素数
a>2?
Y
N
开始
输入a
结束
i
N
i=2
输出a不符合要求
a % i =0
输出a是素数
输出a不是素数
i=i+1
2~a-1都无法被a整除
