2021-2022学年浙教版数学八年级上册 1.4《全等三角形》课时练习(word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版数学八年级上册 1.4《全等三角形》课时练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 108.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览


文档简介
浙教版数学八年级上册1.4
《全等三角形》课时练习
一、选择题
1.下列说法不正确的是(??? )
A.如果两个图形全等,那么它们的形状和大小一定相同。
B.图形全等,只与形状、大小有关,而与它们的位置无关。
C.全等图形的面积相等,面积相等的两个图形是全等形。
D.全等三角形的对应边相等,对应角相等。
2.下列命题中:
⑴形状相同的两个三角形是全等形;
⑵在两个三角形中,相等的角是对应角,相等的边是对应边;
⑶全等三角形对应边上的高、中线及对应角平分线分别相等.
其中真命题的个数有(???? )
A.3个????? B.2个????? C.1个????? D.0个
3.边长都为整数的△ABC≌△DEF,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则 DF的取值为( )
A.3 B.4 C.5 D.3或4或5
4.如图,AB=AD,∠BAO=∠DAO,由此可以得出的全等三角形是(??? )
A.△ABC≌△ADE?? ? B.△ABO≌△ADO C.△AEO≌△ACO?? D.△ABC≌△ADO
5.如图,点E,F在线段BC上,△ABF≌△DCE,AF与DE交于点M.若∠DEC=36°,
则∠AME=( )
A.54° B.60° C.72° D.75°
6.如图,△ABC≌△EFD,则下列说法错误的是( )
A.FC=BD B.EF平行且等于AB C.AC平行且等于DE D.CD=ED
7.有下列说法:
①用同一张底片冲洗出来的两张1寸照片是全等图形;
②所有的正方形是全等图形;
③全等图形的周长相等;
④面积相等的图形一定是全等图形.
其中正确的是( )
A.①②③ B.①③④ C.①③ D.③
8.如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
A.90° B.108° C.110° D.126°
二、填空题
9.如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .
10.如图,△AOB≌△COD,∠AOB=∠COD,∠A=∠C,则∠D的对应角是__________,
图中相等的线段有__________.
11.如图,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠DEF的度数为________.
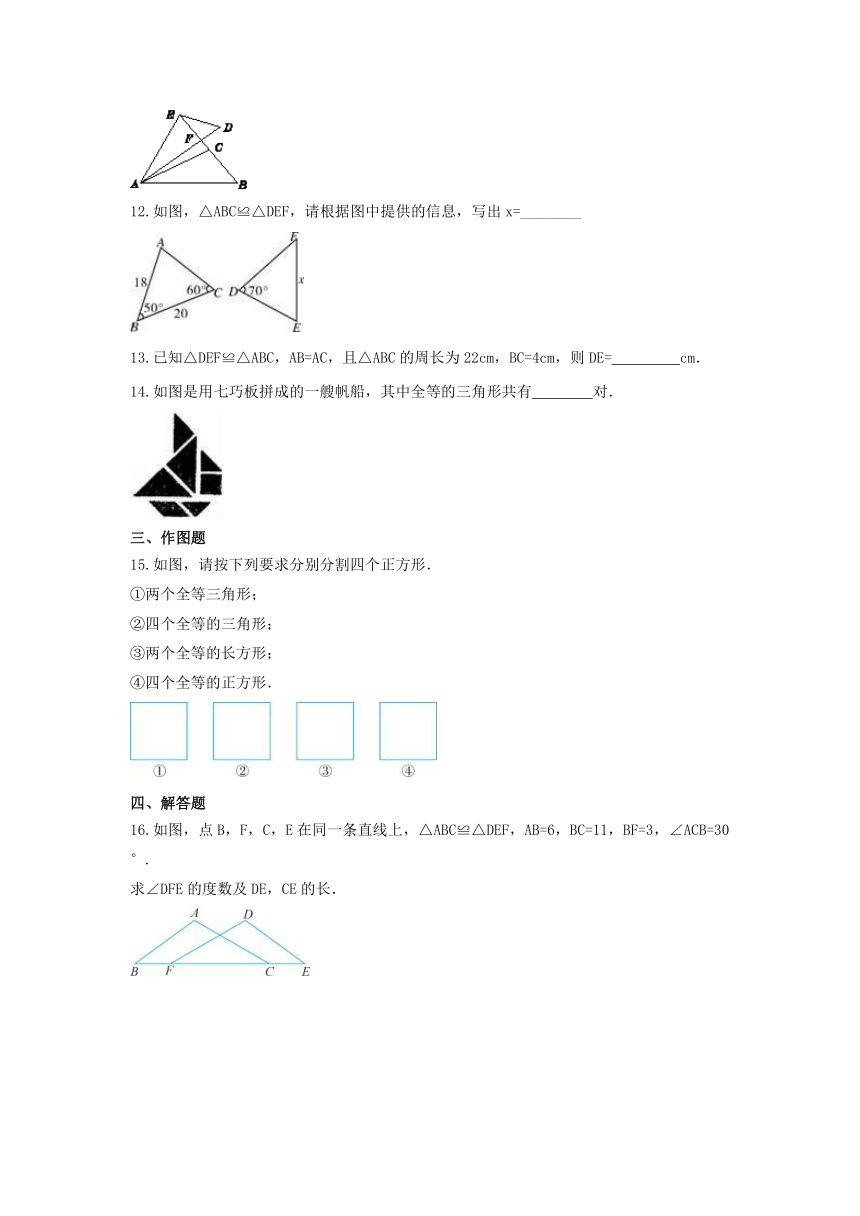
12.如图,△ABC≌△DEF,请根据图中提供的信息,写出x=________
???
13.已知△DEF≌△ABC,AB=AC,且△ABC的周长为22cm,BC=4cm,则DE= cm.
14.如图是用七巧板拼成的一艘帆船,其中全等的三角形共有 对.
三、作图题
15.如图,请按下列要求分别分割四个正方形.
①两个全等三角形;
②四个全等的三角形;
③两个全等的长方形;
④四个全等的正方形.
四、解答题
16.如图,点B,F,C,E在同一条直线上,△ABC≌△DEF,AB=6,BC=11,BF=3,∠ACB=30°.
求∠DFE的度数及DE,CE的长.
17.如图,△ABC≌△ADE,BC延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°.求∠DFB和∠DGB的度数.
18.如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ全等?请说明理由.
参考答案
1.C
2.C
3.B
4.B
5.C.
6.D.
7.C.
8.B
9.答案为:20.
10.答案为:∠OBA,OA=OC、OB=OD、AB=CD
11.答案为:35°.
12.答案为:20
13.答案为:9;
14.答案为:2对
15.解:如解图所示.
16.解:∵△ABC≌△DEF,
∴DE=AB=6,EF=BC=11,∠DFE=∠ACB=30°.
又∵CE=EF-CF,BF=BC-CF,
∴CE=BF=3.
17.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE.
∵∠EAB=∠BAC+∠DAC+∠DAE,∠DAC=10°,∠EAB=120°,
∴∠BAC=∠DAE=55°,
∴∠BAD=∠CAD+∠BAC=65°.
∵∠DFB是△ABF的一个外角,
∴∠DFB=∠BAF+∠B=65°+25°=90°.
∵∠DFB是△DFG的一个外角,
∴∠DFB=∠D+∠DGB,
∴∠DGB=∠DFB-∠D=90°-25°=65°.
18.解:设运动时间为t(s)时,△PEC与△CFQ全等.
∵△PEC与△CFQ全等,∴斜边CP=QC.
当0当6≤t≤14时,点P在BC上.
当0<t<时,点Q在BC上;
当≤t≤时,点Q在AC上.
有三种情况:①当点P在AC上,点Q在BC上时(0易得CP=6-t,QC=8-3t,
∴6-t=8-3t,解得t=1.
②当点P,Q都在AC上时(≤,此时点P,Q重合,如解图②.
易得CP=6-t=3t-8,解得t=3.5.
③当点Q与点A重合,点P在BC上时(6<t≤14),如解图③.
易得CP=t-6,QC=6,∴t-6=6,解得t=12.
综上所述,当点P运动1 s或3.5 s或12s时,△PEC与△CFQ全等.
《全等三角形》课时练习
一、选择题
1.下列说法不正确的是(??? )
A.如果两个图形全等,那么它们的形状和大小一定相同。
B.图形全等,只与形状、大小有关,而与它们的位置无关。
C.全等图形的面积相等,面积相等的两个图形是全等形。
D.全等三角形的对应边相等,对应角相等。
2.下列命题中:
⑴形状相同的两个三角形是全等形;
⑵在两个三角形中,相等的角是对应角,相等的边是对应边;
⑶全等三角形对应边上的高、中线及对应角平分线分别相等.
其中真命题的个数有(???? )
A.3个????? B.2个????? C.1个????? D.0个
3.边长都为整数的△ABC≌△DEF,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则 DF的取值为( )
A.3 B.4 C.5 D.3或4或5
4.如图,AB=AD,∠BAO=∠DAO,由此可以得出的全等三角形是(??? )
A.△ABC≌△ADE?? ? B.△ABO≌△ADO C.△AEO≌△ACO?? D.△ABC≌△ADO
5.如图,点E,F在线段BC上,△ABF≌△DCE,AF与DE交于点M.若∠DEC=36°,
则∠AME=( )
A.54° B.60° C.72° D.75°
6.如图,△ABC≌△EFD,则下列说法错误的是( )
A.FC=BD B.EF平行且等于AB C.AC平行且等于DE D.CD=ED
7.有下列说法:
①用同一张底片冲洗出来的两张1寸照片是全等图形;
②所有的正方形是全等图形;
③全等图形的周长相等;
④面积相等的图形一定是全等图形.
其中正确的是( )
A.①②③ B.①③④ C.①③ D.③
8.如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
A.90° B.108° C.110° D.126°
二、填空题
9.如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .
10.如图,△AOB≌△COD,∠AOB=∠COD,∠A=∠C,则∠D的对应角是__________,
图中相等的线段有__________.
11.如图,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠DEF的度数为________.
12.如图,△ABC≌△DEF,请根据图中提供的信息,写出x=________
???
13.已知△DEF≌△ABC,AB=AC,且△ABC的周长为22cm,BC=4cm,则DE= cm.
14.如图是用七巧板拼成的一艘帆船,其中全等的三角形共有 对.
三、作图题
15.如图,请按下列要求分别分割四个正方形.
①两个全等三角形;
②四个全等的三角形;
③两个全等的长方形;
④四个全等的正方形.
四、解答题
16.如图,点B,F,C,E在同一条直线上,△ABC≌△DEF,AB=6,BC=11,BF=3,∠ACB=30°.
求∠DFE的度数及DE,CE的长.
17.如图,△ABC≌△ADE,BC延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°.求∠DFB和∠DGB的度数.
18.如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ全等?请说明理由.
参考答案
1.C
2.C
3.B
4.B
5.C.
6.D.
7.C.
8.B
9.答案为:20.
10.答案为:∠OBA,OA=OC、OB=OD、AB=CD
11.答案为:35°.
12.答案为:20
13.答案为:9;
14.答案为:2对
15.解:如解图所示.
16.解:∵△ABC≌△DEF,
∴DE=AB=6,EF=BC=11,∠DFE=∠ACB=30°.
又∵CE=EF-CF,BF=BC-CF,
∴CE=BF=3.
17.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE.
∵∠EAB=∠BAC+∠DAC+∠DAE,∠DAC=10°,∠EAB=120°,
∴∠BAC=∠DAE=55°,
∴∠BAD=∠CAD+∠BAC=65°.
∵∠DFB是△ABF的一个外角,
∴∠DFB=∠BAF+∠B=65°+25°=90°.
∵∠DFB是△DFG的一个外角,
∴∠DFB=∠D+∠DGB,
∴∠DGB=∠DFB-∠D=90°-25°=65°.
18.解:设运动时间为t(s)时,△PEC与△CFQ全等.
∵△PEC与△CFQ全等,∴斜边CP=QC.
当0
当0<t<时,点Q在BC上;
当≤t≤时,点Q在AC上.
有三种情况:①当点P在AC上,点Q在BC上时(0
∴6-t=8-3t,解得t=1.
②当点P,Q都在AC上时(≤,此时点P,Q重合,如解图②.
易得CP=6-t=3t-8,解得t=3.5.
③当点Q与点A重合,点P在BC上时(6<t≤14),如解图③.
易得CP=t-6,QC=6,∴t-6=6,解得t=12.
综上所述,当点P运动1 s或3.5 s或12s时,△PEC与△CFQ全等.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
