第三章一元一次不等式 知识梳理及单元检测 2021—2022学年浙教版数学八年级上册(无答案)
文档属性
| 名称 | 第三章一元一次不等式 知识梳理及单元检测 2021—2022学年浙教版数学八年级上册(无答案) | 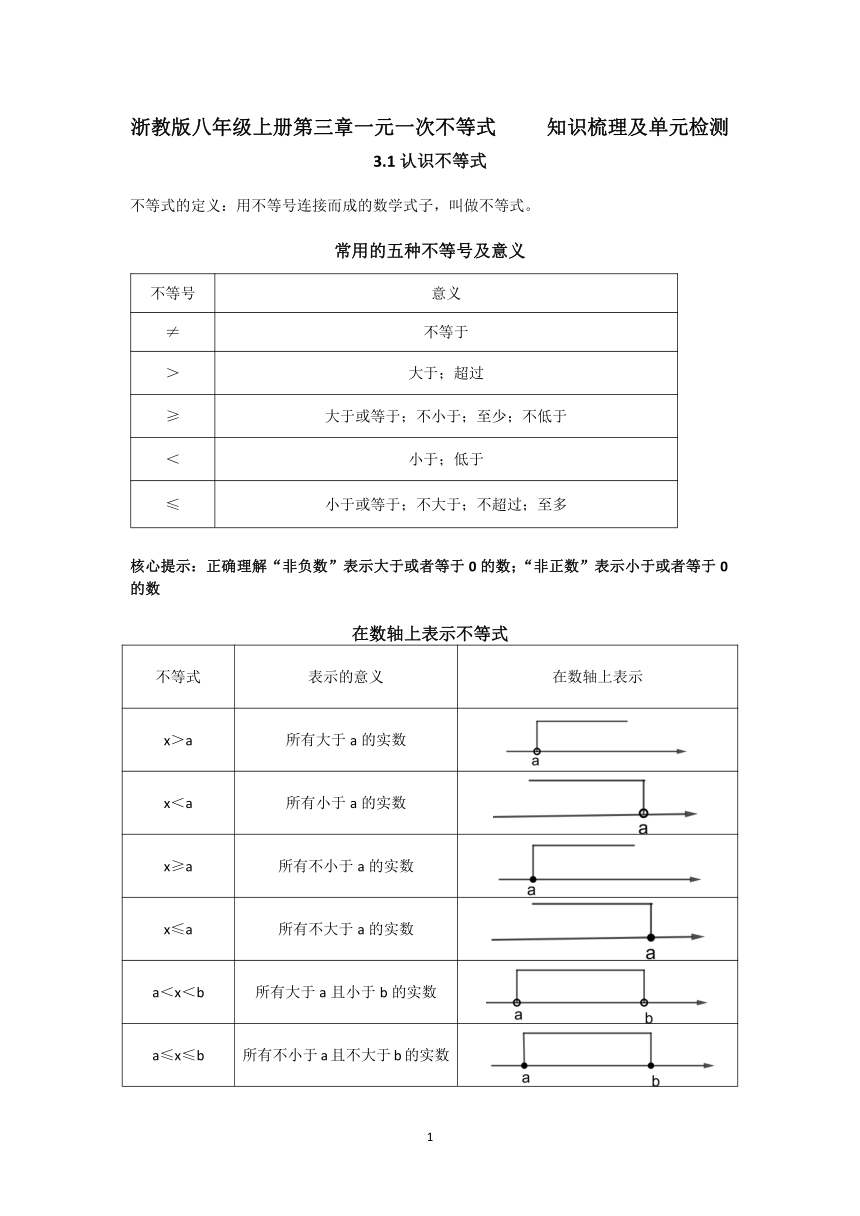 | |
| 格式 | doc | ||
| 文件大小 | 230.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 09:40:02 | ||
图片预览



文档简介
浙教版八年级上册第三章一元一次不等式 知识梳理及单元检测
3.1认识不等式
不等式的定义:用不等号连接而成的数学式子,叫做不等式。
常用的五种不等号及意义
不等号 意义
≠ 不等于
> 大于;超过
≥ 大于或等于;不小于;至少;不低于
< 小于;低于
≤ 小于或等于;不大于;不超过;至多
核心提示:正确理解“非负数”表示大于或者等于0的数;“非正数”表示小于或者等于0的数
在数轴上表示不等式
不等式 表示的意义 在数轴上表示
x>a 所有大于a的实数
x<a 所有小于a的实数
x≥a 所有不小于a的实数
x≤a 所有不大于a的实数
a<x<b 所有大于a且小于b的实数
a≤x≤b 所有不小于a且不大于b的实数
a<x≤b 所有大于a且不大于b的实数
a≤x<b 所有不小于a且小于b的实数
核心提示:大于向右,小于向左;有等号用实心点,无等号用空心点。
3.2不等式的基本性质
性质名称 内容 数学式子表示
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
核心提示:在进行性质的应用时,必须对不等式左右两边同时进行,对不等式两边运算必须是同一个(即必须同时加、减、乘、除同一个数)
在进行同时乘除一个负数时需要对不等式符号改变方向
3.3一元一次不等式解法
解一元一次不等式
序号 步骤 依据
1 去分母 不等式的基本性质3
2 去括号 去括号法则和单项式乘多项式法则
3 移项 不等式的性质2
4 合并同类型 合并同类型法则
5 系数化为1 不等式的基本性质3
列一元一次不等式解决实际问题
审 找出题目中所给出的不等关系
设 设适当的未知数,表示出相关的量
列 根据不等式关系列出一元一次不等式
解 解出一元一次不等式的解
答 检验解是否符合实际问题
3.4一元一次不等式组
最简不等式组 各个一元一次不等式的解在数轴上的表示 不等式组的解 记忆口诀
x>a
x>b
x<a
x<b
x<a
x>b
x>a
x<b
浙教版八年级上册第三章一元一次不等式 单元检测卷
选择题(每题3分,共30分)
1.不等式组的解集在数轴上表示为( )
A. B. C. D.
2.已知a,b为实数,则下列结论正确的是( )
A、若a>b,则a﹣c<b﹣c B、若a>b,则﹣a+c>﹣b+c
C、若a>b,则ac2>bc2 D、若ac2>bc2 , 则a>b
3.不等式组的解集是………………………………………………………( )
A.x>-1 B.x<2
C.2<x<3 D.无解
4.不等式组的解集是x>﹣1,则m的值是( )
A.﹣1 B.﹣2 C.1 D.2
5.若不等式x≤m的解都是不等式x≤2的解,则m的取值范围是( )
A.m≤2 B.m≥2 C.m<2 D.m>2
6.某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过95分,他至少要答对( )道题.
A. 12 B. 13 C. 14 D. 15
7.不等式-3≥2(x-3)的非负整数解有( )
A.4个 B.3个 C.2个 D.1个
8.如果不等式组只有一个整数解,那么a的取值范围是( )
A. 39.若a>1,则M=a,N=,P=的大小关系为( )
A.P>N>M B.M>N>P C.N>P>M D.M>P>N
10.某市某化工厂现有A种原料52 kg,B种原料64 kg,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3 kg,B种原料2 kg;生产1件乙种产品需要A种原料2 kg,B种原料4 kg,则生产方案的种数为( )
A. 4 B. 5
C. 6 D. 6
二、填空题(每题4分,共24分)
11.用不等式表示:y与x的和小于x的2倍,________
12.若a>b,则1-a__________1-b
13.若(m﹣1)x≥m﹣1的解集是x≤1,则m的取值范围是________
14.若关于x的一元一次不等式组有2个负整数解,则a的取值范围是
15.乐乐用100元需购笔记本和钢笔共30件,若每本笔记本2元,每支钢笔5元,那么乐乐最多能买???? ???????支钢笔
16.若关于x的不等式x﹣b>0恰有两个负整数解,则b的取值范围为________
某班有48名学生会下象棋或围棋,会下象棋的人数比会下围棋的人数的2倍少3人,两种棋都会下的至多有9人,但不少于5人,则会下围棋的有___________人.
三、解答题
17.(6分)解不等式(组),并把解集在数轴上表示出来.
(1)1->; (2)
18.(6分)阅读如图所示的计算程序:
(1)当x=1000时,输出的y的值是多少
(2)若经过二次输入才能输出y的值,求x的取值范围.
19.(6分)试确定实数a的取值范围,使不等式组恰好有两个整数解.
20.(8分)已知关于x,y的二元一次方程组的解中,x为非正数,y为负数.
(1)求a的取值范围.
(2)化简:|a-3|+|a+2|.
(3)在a的取值范围中,当a为何整数时,不等式2ax+x<2a+1的解为x>1
21.(6分)当k满足条件时,关于x的一元二次方程kx2+(k﹣1)x+k2+3k=0是否存在实数根x=0?若存在求出k值,若不存在请说明理由.
22.(6分)绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王灿如何安排甲、乙两种货车可一次性地运到销售地有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?
23.(8分)我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用〈a〉表示大于a的最小整数,例如:〈2.5〉=3,〈4〉=5,〈-1.5〉=-1.解决下列问题:
(1)[-4.5]=_________,〈3.5〉=___________.
(2)若[x]=2,则x的取值范围是____________;若〈y〉=-1,则y的取值范围是_________
(3)已知x,y满足方程组求x,y的取值范围
3.1认识不等式
不等式的定义:用不等号连接而成的数学式子,叫做不等式。
常用的五种不等号及意义
不等号 意义
≠ 不等于
> 大于;超过
≥ 大于或等于;不小于;至少;不低于
< 小于;低于
≤ 小于或等于;不大于;不超过;至多
核心提示:正确理解“非负数”表示大于或者等于0的数;“非正数”表示小于或者等于0的数
在数轴上表示不等式
不等式 表示的意义 在数轴上表示
x>a 所有大于a的实数
x<a 所有小于a的实数
x≥a 所有不小于a的实数
x≤a 所有不大于a的实数
a<x<b 所有大于a且小于b的实数
a≤x≤b 所有不小于a且不大于b的实数
a<x≤b 所有大于a且不大于b的实数
a≤x<b 所有不小于a且小于b的实数
核心提示:大于向右,小于向左;有等号用实心点,无等号用空心点。
3.2不等式的基本性质
性质名称 内容 数学式子表示
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
核心提示:在进行性质的应用时,必须对不等式左右两边同时进行,对不等式两边运算必须是同一个(即必须同时加、减、乘、除同一个数)
在进行同时乘除一个负数时需要对不等式符号改变方向
3.3一元一次不等式解法
解一元一次不等式
序号 步骤 依据
1 去分母 不等式的基本性质3
2 去括号 去括号法则和单项式乘多项式法则
3 移项 不等式的性质2
4 合并同类型 合并同类型法则
5 系数化为1 不等式的基本性质3
列一元一次不等式解决实际问题
审 找出题目中所给出的不等关系
设 设适当的未知数,表示出相关的量
列 根据不等式关系列出一元一次不等式
解 解出一元一次不等式的解
答 检验解是否符合实际问题
3.4一元一次不等式组
最简不等式组 各个一元一次不等式的解在数轴上的表示 不等式组的解 记忆口诀
x>a
x>b
x<a
x<b
x<a
x>b
x>a
x<b
浙教版八年级上册第三章一元一次不等式 单元检测卷
选择题(每题3分,共30分)
1.不等式组的解集在数轴上表示为( )
A. B. C. D.
2.已知a,b为实数,则下列结论正确的是( )
A、若a>b,则a﹣c<b﹣c B、若a>b,则﹣a+c>﹣b+c
C、若a>b,则ac2>bc2 D、若ac2>bc2 , 则a>b
3.不等式组的解集是………………………………………………………( )
A.x>-1 B.x<2
C.2<x<3 D.无解
4.不等式组的解集是x>﹣1,则m的值是( )
A.﹣1 B.﹣2 C.1 D.2
5.若不等式x≤m的解都是不等式x≤2的解,则m的取值范围是( )
A.m≤2 B.m≥2 C.m<2 D.m>2
6.某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过95分,他至少要答对( )道题.
A. 12 B. 13 C. 14 D. 15
7.不等式-3≥2(x-3)的非负整数解有( )
A.4个 B.3个 C.2个 D.1个
8.如果不等式组只有一个整数解,那么a的取值范围是( )
A. 3
A.P>N>M B.M>N>P C.N>P>M D.M>P>N
10.某市某化工厂现有A种原料52 kg,B种原料64 kg,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3 kg,B种原料2 kg;生产1件乙种产品需要A种原料2 kg,B种原料4 kg,则生产方案的种数为( )
A. 4 B. 5
C. 6 D. 6
二、填空题(每题4分,共24分)
11.用不等式表示:y与x的和小于x的2倍,________
12.若a>b,则1-a__________1-b
13.若(m﹣1)x≥m﹣1的解集是x≤1,则m的取值范围是________
14.若关于x的一元一次不等式组有2个负整数解,则a的取值范围是
15.乐乐用100元需购笔记本和钢笔共30件,若每本笔记本2元,每支钢笔5元,那么乐乐最多能买???? ???????支钢笔
16.若关于x的不等式x﹣b>0恰有两个负整数解,则b的取值范围为________
某班有48名学生会下象棋或围棋,会下象棋的人数比会下围棋的人数的2倍少3人,两种棋都会下的至多有9人,但不少于5人,则会下围棋的有___________人.
三、解答题
17.(6分)解不等式(组),并把解集在数轴上表示出来.
(1)1->; (2)
18.(6分)阅读如图所示的计算程序:
(1)当x=1000时,输出的y的值是多少
(2)若经过二次输入才能输出y的值,求x的取值范围.
19.(6分)试确定实数a的取值范围,使不等式组恰好有两个整数解.
20.(8分)已知关于x,y的二元一次方程组的解中,x为非正数,y为负数.
(1)求a的取值范围.
(2)化简:|a-3|+|a+2|.
(3)在a的取值范围中,当a为何整数时,不等式2ax+x<2a+1的解为x>1
21.(6分)当k满足条件时,关于x的一元二次方程kx2+(k﹣1)x+k2+3k=0是否存在实数根x=0?若存在求出k值,若不存在请说明理由.
22.(6分)绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王灿如何安排甲、乙两种货车可一次性地运到销售地有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?
23.(8分)我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3;用〈a〉表示大于a的最小整数,例如:〈2.5〉=3,〈4〉=5,〈-1.5〉=-1.解决下列问题:
(1)[-4.5]=_________,〈3.5〉=___________.
(2)若[x]=2,则x的取值范围是____________;若〈y〉=-1,则y的取值范围是_________
(3)已知x,y满足方程组求x,y的取值范围
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
