第1章 三角形的初步知识(含解析)-2021年暑假浙教版八年级数学上册预习自学测试卷
文档属性
| 名称 | 第1章 三角形的初步知识(含解析)-2021年暑假浙教版八年级数学上册预习自学测试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 188.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 17:46:09 | ||
图片预览




文档简介
第1章 三角形的初步知识-2021年暑假浙教版八年级数学上册预习自学测试卷
一、选择题
1.有下列命题:①对顶角相等;②同位角相等,两直线平行;③若a=b,则|a|=|b|;④全等三角形的对应角相等.它们的逆命题一定成立的有(????? )
A.?①②③④????????????????????????B.?①④???????????????C.?②④????????????????????????D.?②
2.如图,点D,E在△ABC的边BC上,△ABD≌△ACE,其中B,C为对应顶点,D,E为对应顶点,下列结论不一定成立的是(?? )
A.?AC=CD????????B.?BE=CD??????????C.?∠ADE=∠AED?????D.?∠BAE=∠CAD
3.如图,△ABC≌△DEF,BC=7,EC=4,则CF的长为(?? )
A.?2??????????????????????????B.?3?????????????????????C.?5??????????????????????????D.?7
4.如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是(??? )
A.?∠1=∠2??????????????B.?CA=AC????????????????????????C.?∠D=∠B????????????D.?AC=BC
5.如图,在 △ABC 中, ∠C=90°. 用直尺和圆规在边BC上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是(?? )
A.?????B.?????C.????????D.?
6.如图所示,∠A0B = 40°,OC平分∠AOB,直尺与OC垂直,则∠1等于(?? )
A.?60°???????????????????????B.?70°?????????????????C.?50°??????????????????????????????D.?40°
7.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为(?? )
A.?1cm?????????????????????????????????????B.?2cm?????????????????????????????????????C.?5cm?????????????????????????????????????D.?8cm
8.如图所示,在△ABC中,∠C = 90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC = ∠BDE;③DE平分∠ADB;④若AC = 4BE,则S△ABC = 8S△BDE.其中正确的有(?? )
A.?1个???????????????????B.?2个???????????????????????C.?3个?????????????????????????D.?4个
9.在 △ABC 中,已知 AC:BC:AB=5:12:13 ,AD是 △ABC 的角平分线, DE⊥AB 于点E.若 △ABC 的面积为S,则 △ACD 的面积为(?? )
A.?14S?????????????????????????B.?518S?????????????????????????C.?625S????????????????????D.?725S
10.如图所示,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角平分线与∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点.若∠BOC = 120°,则∠D的度数为(?????? )
A.?15°????????????????????????B.?20°?????????????????C.?25°?????????????????????????????D.?30°
二、填空题
11.一张小凳子的结构如图所示, ∠1=∠2 ,若 ∠3=120° ,则 ∠1 的度数为________.
12.如图,在△ABC中,点E在AB上,D为AC的中点,过点C作CF∥AB交ED的延长线于点F.若AB=15cm,CF=10cm,则BE=________cm.
13.如图所示,在Rt△ABC中,∠C = 90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 12 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD = 6,AB = 20,则△ABD的面积是 ________ .
14.如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=52°,则∠1+∠2的度数为________.
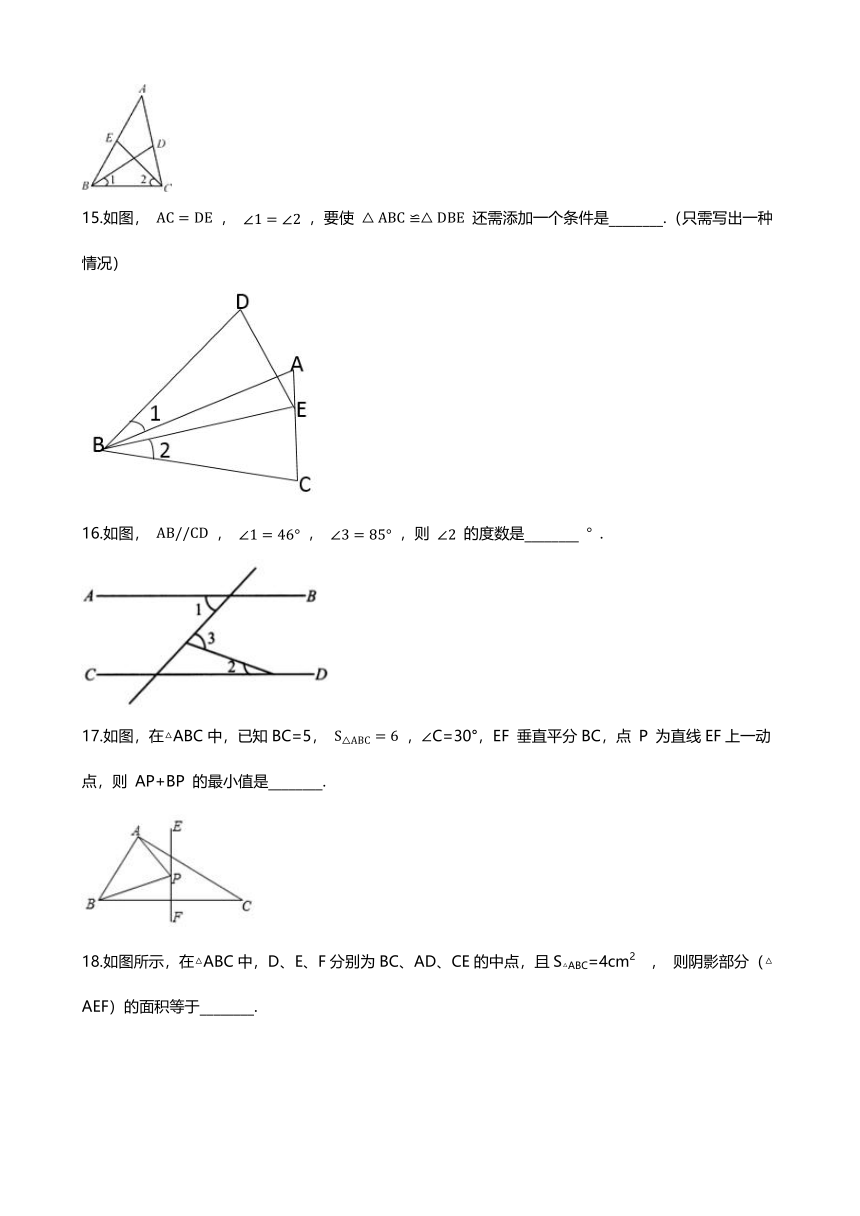
15.如图, AC=DE , ∠1=∠2 ,要使 △ABC≌△DBE 还需添加一个条件是________.(只需写出一种情况)
16.如图, AB//CD , ∠1=46° , ∠3=85° ,则 ∠2 的度数是________ ° .
17.如图,在△ABC中,已知BC=5, S△ABC=6 ,∠C=30°,EF 垂直平分BC,点 P 为直线EF上一动点,则 AP+BP 的最小值是________.
18.如图所示,在△ABC中,D、E、F分别为BC、AD、CE的中点,且S△ABC=4cm2 , 则阴影部分(△AEF)的面积等于________.
三、解答题
19.在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.
请你从这四个条件中选出三个作为题设,另一个作为结论,
组成一个真命题,并给予证明.
题设:________;结论:________.(均填写序号)
证明:
20.??? 已知:如图, CD=BE , CD//BE , ∠D=∠E. 求证:点C是线段AB的中点.
21.如图, AB=AC , AD=AE , ∠BAD=∠CAE ,求证: ∠D=∠E .
22.如图,点G在CA的延长线上,AF= AG,AD⊥BC,GE⊥BC
求证:AD平分∠BAC,
证明:AF=AG(已知),
∴∠AGF=∠AFG(________),
∵AD⊥BC,GE⊥BC(已知) ,
∴∠ADC=∠GEC=90°(________?),
∴AD∥GE (________),
∴∠CAD=________(两直线平行,同位角相等)
∠BAD=∠AFG (________),
∴∠CAD=∠BAD(等量代换)
∴AD平分∠BAC (________)
?
23.如图,在△ABC中,∠C=90°,∠A=40°.
(1)在AC边上确定点D , 使点D到边AB的距离等于DC的长(用尺规作图,保留作图痕迹,不要求写作法);
?
(2)在(1)的条件下,连结BD , 求∠ADB的度数.
24.如图,AC与BD相交于点O,且 OA=OC , OB=OD .
(1)求证: AB//CD ;
(2)直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.
25.如图1,AD平分∠BAC,AE⊥BC,∠B=30°,∠C=70°。
(1)∠BAC=________°, ∠DAE=________°;
(2)如图2,若把“AE⊥BC"变成“点F在AD的延长线上,FE⊥BC“,其它条件不变,求∠DFE的度数;
(3)如图3,AD平分∠BAC,AE平分∠BEC,∠C-∠B=40°,求∠DAE的度数。
答案
一、选择题
1.解: ①逆命题是:相等的角是对顶角,错误; ②逆命题是:两直线平行,同位角相等,正确; ③逆命题是:若|a|=|b|,则a=b,如-2=2 , 错误; ④逆命题是:对应角相等的两个三角形是全等三角形,如两个三角形相似,对应角相等,但不全等.?错误;
综上,正确的是②?.
故答案为:D.
2.解:∵△ABD≌△ACE,
∴BD=CE,
∴BE=CD,B成立,不符合题意;
∵△ABD≌△ACE,
∴∠ADB=∠AEC,
∴∠ADE=∠AED,C成立,不符合题意;
∵△ABD≌△ACE,
∴∠BAD=∠CAE,
∴∠BAE=∠CAD,D成立,不符合题意;
AC不一定等于CD,A不成立,符合题意,
故答案为:A.
3.解:∵△ABC≌△DEF,
∴EF=BC=7,
∵EC=4,
∴CF=3,
故答案为:B.
4.解:∵△ABC≌△CDA,AB=CD,
∴∠1和∠2,∠D和∠B是对应角,
∴∠1=∠2,∠D=∠B,
∴AC和CA是对应边,而不是BC,
∴A、B、C正确,D、AC=BC错误.
故答案为:D.
5.解: ∵ 点P到点A、点B的距离相等,
∴ 点P在线段AB的垂直平分线上,
故答案为:C.
6.解:如图,取∠2,
∵OC平分∠AOB,
∴∠AOC=20°,
∴∠2=90°-∠AOC=70°,
∴∠3=∠2=70°,
∵直尺对边平行,
∴∠1=∠3=70°.
故答案为:B.
7.解:设第三边长xcm.
根据三角形的三边关系,得2<x<8.
∵5cm在第三边长的取值范围内,所以此三角形的第三边长可能为5cm.
故答案为:C.
8.解:∵ AD平分∠BAC,
∴∠DAC=∠DAE.
∵∠C=90°, DE⊥AB,
∴∠C=∠E=90°.
∵AD=AD,∠DAC=∠DAE,∠C=∠E=90°,
∴△DAC≌△DAE,
∴∠CDA=∠EDA,
∴① AD平分∠CDE ,正确.
无法证明∠BDE=60°,
∴③ DE平分∠ADB错误.
∵BE+AE=AB,AE=AC,AC=4BE,
∴AB=5BE,AE=4BE,
∴S△ADB=5S△BDE , S△ADC=4S△BDE ,
∴S△ABC=9S△BDE , ④错误.
∵∠BDE=90°-∠B,∠BAC=90°-∠B,
∴∠BDE=∠BAC,
∴②∠BAC=∠BDE正确.
故答案为:B.
9.解:
∵ AC:BC:AB=5:12:13 ,
∵AD是 △ABC 的角平分线, DE⊥AB ,
∴∠CAD=∠BAD,∠C=∠AED =90°,
∵AD=AD,
∴ △ACD?△AED ,
∴ S△ACD=S△AED ,AE=AC=5k,
∴BE=13k-5k=8k,
∵ △AED 和 △BED 同高,
∴ S△BED:S△AED=8:5 ,
∵ △ABC 的面积为S,
∴ S△ACD=518S .
故答案为:B.
10.解:对图形进行点标注,如图所示:
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB.
∵∠ABC+∠ACB+∠A=180°,
∴2∠OBC+2∠OBC+∠A=180°,
∴∠OCB+∠OBC=90°-12∠A.
∵∠OCB+∠OBC+∠BOC=180°,
∴90°-12∠A+∠BOC=180°,
∴∠BOC=90°+12∠A.
而∠BOC=120°,
∴∠A=60°.
∵∠DCF=∠D+∠DBC,∠ACF=∠ABC+∠A,BD平分∠ABC,DC平分∠ACF,
∴∠ACF=2∠DCF,∠ABC=2∠DBC,
∴2∠D+2∠DBC=∠ABC+∠A,
∴2∠D=∠A,即∠D=12∠A.
∵∠A=60°,
∴∠D=30°.
故答案为:D.
二、填空题
11.解:∵∠3=∠1+∠2,∠1=∠2,∠3=120°,
∴ ∠1=12∠3=60° ,
故答案为:60°.
12.解:∵D为AC的中点
∴ AD=CD
∵CF∥AB
∴ ∠AED=∠F,∠A=∠FCD
在 △AED 和 △CFD 中{AD=CD∠AED=∠F∠A=∠FCD
∴ △AED≌△CFD (AAS)
∴ AE=CF
∵AB=15cm,CF=10cm,
BE=AB-AE=AB-CF=15-10=5cm
故答案为:5.
13.解:由作图步骤可知:AP为∠CAB的角平分线.
过点D作DE⊥AB于点E,则CD=DE=6.
∵DE=6,AB=20,
∴△ABD的面积=12×DE×AB=12×6×20=60.
故答案为:60.
14.解:∵∠A=52°,∴∠ABC+∠ACB=128°.
∵BD和CE是△ABC的两条角平分线,
∴∠1= 12 ∠ABC,∠2= 12 ∠ACB,
∴∠1+∠2= 12 (∠ABC+∠ACB)=64°.
故答案为:64°.
15.解:添加条件为∠A=∠D,理由是:
∵ ∠1=∠2 ,
∴∠ABC=∠DBE,
在△ABC和△DBE中,
{∠A=∠DAC=DE∠ABC=∠DBE ,
∴ △ABC≌△DBE (AAS),
故答案为:∠A=∠D.
16.解:如图所示:
∵AB∥CD,∠1=46°,
∴∠4=∠1=46°,
∵∠3=85°,
∴∠2=∠3-∠4=39°;
故答案为39.
17.解:过点A作AD⊥BC于点D,
∵EF 垂直平分BC,
∴当点P与EF和AC的交点重合时,BP=CP???
∴AP+BP=AC
两点之间线段最短,此时AP+BP的值最小,
∵S△ABC=12BC·AD=6
解之:AD=125
在Rt△ADC中,∠C=30°
∴AC=2AD=245.
故答案为:245.
18.解:∵ D、E、F分别为BC、AD、CE的中点, S△ABC=4cm2 ,
∴S△AEF=12S△ACE=12×12S△ACD=12×12×12S△ABC=18×4=12=0.5(cm2).
故答案为:0.5cm2.
三、解答题
19.解:情况一:题设①②③,结论④;
∵BF=EC,
∴ BF+CF=EC+CF ,
即 BC=EF ,
在△ABC和△DEF中,
{AB=DE∠B=∠EBC=EF ,
∴ △ABC?△DEF ,
∴ ∠1=∠2 ;
情况二:题设①③④,结论③;
在△ABC和△DEF中,
{∠1=∠2∠B=∠EAB=DE ,
∴ △ABC?△DEF ,
∴ BC=EF ,
∴ BC-FC=EF-FC ,即 BF=EC ;
情况三:题设②③④,结论①;
∵ BF=EC ,
∴ BF+CF=EC+CF ,
即 BC=EF ,
在△ABC和△DEF中,
{∠1=∠2BC=EF∠B=∠E ,
∴ △ABC?△DEF ,
∴ AB=DE ;
故答案为:①②③;④.
20. 证明: ∵CD//BE ,
∴∠ACD=∠B ,
在 △ACD 和 △CBE 中,
{∠ACD=∠BCD=BE∠D=∠E ,
∴△ACD ≌ △CBE(ASA) ,
∴AC=BC ,
则点C是线段AB的中点.
21. 证明:
∵ ∠BAD=∠CAE
∴ ∠BAD+∠BAC=∠CAE+∠BAC
即 ∠CAD=∠BAE
∴在 △ADC 与 △AEB 中
{AD=AE∠CAD=∠BAEAC=AB
∴ △ADC≌△AEB(SAS)
∴ ∠D=∠E
22. 等边对等角;垂直的定义;同位角相等,两直线平行;∠AGE;两直线平行,内错角相等;角平分线定义
求证:AD平分∠BAC,
证明:AF=AG(已知),
∴∠AGF=∠AFG(等边对等角),
∵AD⊥BC,GE⊥BC(已知) ,
∴∠ADC=∠GEC=90°(垂直的定义),
∴AD∥GE (同位角相等,两直线平行),
∴∠CAD=∠AGE(两直线平行,同位角相等)
∠BAD=∠AFG (两直线平行,内错角相等),
∴∠CAD=∠BAD(等量代换)
∴AD平分∠BAC (角平分线定义).
23. (1)解:如图,点D即为所求,
?(2)解:∵∠A=40°,∠C=90°,
∴∠ABC=90°-40°=50°,
∵BD平分∠ABC,
∴∠ABD=12∠ABC=25°,
∴∠ADB=180°-40°-25°=115°.
24. (1)证明:由题可知,
在△AOB与△COD中,
{AO=OC∠AOB=∠CODOB=OD ,
∵ΔAOB≌ΔCOD(SAS) ,
∴∠B=∠D ,
∴AB//CD ;
(2)OE=OF,理由如下:
由(1)可知: ΔAOB?ΔCOD ,
∴∠A=∠C,
在△AOE于△COF中,{∠A=∠CAO=CO∠AOE=∠COF
∴ΔAOE≌ΔCOF(ASA) ,
∴OE=OF .
25. (1)80;20
(2)解:20°
(3)解:20°
解:(1)∠BAC=180°-∠B-∠C=180°-30°-70°=80°;
∵AD平分∠BAC,
∴∠DAC=12∠BAC=40°,
∵AE⊥BC,
∴∠CAE=90°-∠C=90°-70°=20°,
∴∠DAE=∠DAC-∠CAE=40°-20°=20°.
(2)∵∠ADC=180°-∠C-∠DAC=180°-70°-40°=70°,
∴∠EDF=∠ADC=70°,
∵FE⊥BC,
∴∠DFE=90°-∠EDF=90°-70°=20°;
(3)∵∠B+∠BEA+∠BAE=180°,∠C+∠CEA+∠CAE=180°,
∵AE平分∠BEC,即∠BEA=∠CEA,
∴∠C-∠B=∠BAE-∠CAE=40°,
∴∠BAD+∠DAE-(∠CAD-∠DAE)=40°,
∵AE平分∠BAC,即∠BAD=∠CAD,
∴2∠DAE=40°,
∴∠DAE=20°.
一、选择题
1.有下列命题:①对顶角相等;②同位角相等,两直线平行;③若a=b,则|a|=|b|;④全等三角形的对应角相等.它们的逆命题一定成立的有(????? )
A.?①②③④????????????????????????B.?①④???????????????C.?②④????????????????????????D.?②
2.如图,点D,E在△ABC的边BC上,△ABD≌△ACE,其中B,C为对应顶点,D,E为对应顶点,下列结论不一定成立的是(?? )
A.?AC=CD????????B.?BE=CD??????????C.?∠ADE=∠AED?????D.?∠BAE=∠CAD
3.如图,△ABC≌△DEF,BC=7,EC=4,则CF的长为(?? )
A.?2??????????????????????????B.?3?????????????????????C.?5??????????????????????????D.?7
4.如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是(??? )
A.?∠1=∠2??????????????B.?CA=AC????????????????????????C.?∠D=∠B????????????D.?AC=BC
5.如图,在 △ABC 中, ∠C=90°. 用直尺和圆规在边BC上确定一点P,使点P到点A、点B的距离相等,则符合要求的作图痕迹是(?? )
A.?????B.?????C.????????D.?
6.如图所示,∠A0B = 40°,OC平分∠AOB,直尺与OC垂直,则∠1等于(?? )
A.?60°???????????????????????B.?70°?????????????????C.?50°??????????????????????????????D.?40°
7.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为(?? )
A.?1cm?????????????????????????????????????B.?2cm?????????????????????????????????????C.?5cm?????????????????????????????????????D.?8cm
8.如图所示,在△ABC中,∠C = 90°,AD平分∠BAC交BC于点D,DE⊥AB于点E,则下列结论:①AD平分∠CDE;②∠BAC = ∠BDE;③DE平分∠ADB;④若AC = 4BE,则S△ABC = 8S△BDE.其中正确的有(?? )
A.?1个???????????????????B.?2个???????????????????????C.?3个?????????????????????????D.?4个
9.在 △ABC 中,已知 AC:BC:AB=5:12:13 ,AD是 △ABC 的角平分线, DE⊥AB 于点E.若 △ABC 的面积为S,则 △ACD 的面积为(?? )
A.?14S?????????????????????????B.?518S?????????????????????????C.?625S????????????????????D.?725S
10.如图所示,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角平分线与∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点.若∠BOC = 120°,则∠D的度数为(?????? )
A.?15°????????????????????????B.?20°?????????????????C.?25°?????????????????????????????D.?30°
二、填空题
11.一张小凳子的结构如图所示, ∠1=∠2 ,若 ∠3=120° ,则 ∠1 的度数为________.
12.如图,在△ABC中,点E在AB上,D为AC的中点,过点C作CF∥AB交ED的延长线于点F.若AB=15cm,CF=10cm,则BE=________cm.
13.如图所示,在Rt△ABC中,∠C = 90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 12 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD = 6,AB = 20,则△ABD的面积是 ________ .
14.如图,在△ABC中,BD和CE是△ABC的两条角平分线.若∠A=52°,则∠1+∠2的度数为________.
15.如图, AC=DE , ∠1=∠2 ,要使 △ABC≌△DBE 还需添加一个条件是________.(只需写出一种情况)
16.如图, AB//CD , ∠1=46° , ∠3=85° ,则 ∠2 的度数是________ ° .
17.如图,在△ABC中,已知BC=5, S△ABC=6 ,∠C=30°,EF 垂直平分BC,点 P 为直线EF上一动点,则 AP+BP 的最小值是________.
18.如图所示,在△ABC中,D、E、F分别为BC、AD、CE的中点,且S△ABC=4cm2 , 则阴影部分(△AEF)的面积等于________.
三、解答题
19.在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.
请你从这四个条件中选出三个作为题设,另一个作为结论,
组成一个真命题,并给予证明.
题设:________;结论:________.(均填写序号)
证明:
20.??? 已知:如图, CD=BE , CD//BE , ∠D=∠E. 求证:点C是线段AB的中点.
21.如图, AB=AC , AD=AE , ∠BAD=∠CAE ,求证: ∠D=∠E .
22.如图,点G在CA的延长线上,AF= AG,AD⊥BC,GE⊥BC
求证:AD平分∠BAC,
证明:AF=AG(已知),
∴∠AGF=∠AFG(________),
∵AD⊥BC,GE⊥BC(已知) ,
∴∠ADC=∠GEC=90°(________?),
∴AD∥GE (________),
∴∠CAD=________(两直线平行,同位角相等)
∠BAD=∠AFG (________),
∴∠CAD=∠BAD(等量代换)
∴AD平分∠BAC (________)
?
23.如图,在△ABC中,∠C=90°,∠A=40°.
(1)在AC边上确定点D , 使点D到边AB的距离等于DC的长(用尺规作图,保留作图痕迹,不要求写作法);
?
(2)在(1)的条件下,连结BD , 求∠ADB的度数.
24.如图,AC与BD相交于点O,且 OA=OC , OB=OD .
(1)求证: AB//CD ;
(2)直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.
25.如图1,AD平分∠BAC,AE⊥BC,∠B=30°,∠C=70°。
(1)∠BAC=________°, ∠DAE=________°;
(2)如图2,若把“AE⊥BC"变成“点F在AD的延长线上,FE⊥BC“,其它条件不变,求∠DFE的度数;
(3)如图3,AD平分∠BAC,AE平分∠BEC,∠C-∠B=40°,求∠DAE的度数。
答案
一、选择题
1.解: ①逆命题是:相等的角是对顶角,错误; ②逆命题是:两直线平行,同位角相等,正确; ③逆命题是:若|a|=|b|,则a=b,如-2=2 , 错误; ④逆命题是:对应角相等的两个三角形是全等三角形,如两个三角形相似,对应角相等,但不全等.?错误;
综上,正确的是②?.
故答案为:D.
2.解:∵△ABD≌△ACE,
∴BD=CE,
∴BE=CD,B成立,不符合题意;
∵△ABD≌△ACE,
∴∠ADB=∠AEC,
∴∠ADE=∠AED,C成立,不符合题意;
∵△ABD≌△ACE,
∴∠BAD=∠CAE,
∴∠BAE=∠CAD,D成立,不符合题意;
AC不一定等于CD,A不成立,符合题意,
故答案为:A.
3.解:∵△ABC≌△DEF,
∴EF=BC=7,
∵EC=4,
∴CF=3,
故答案为:B.
4.解:∵△ABC≌△CDA,AB=CD,
∴∠1和∠2,∠D和∠B是对应角,
∴∠1=∠2,∠D=∠B,
∴AC和CA是对应边,而不是BC,
∴A、B、C正确,D、AC=BC错误.
故答案为:D.
5.解: ∵ 点P到点A、点B的距离相等,
∴ 点P在线段AB的垂直平分线上,
故答案为:C.
6.解:如图,取∠2,
∵OC平分∠AOB,
∴∠AOC=20°,
∴∠2=90°-∠AOC=70°,
∴∠3=∠2=70°,
∵直尺对边平行,
∴∠1=∠3=70°.
故答案为:B.
7.解:设第三边长xcm.
根据三角形的三边关系,得2<x<8.
∵5cm在第三边长的取值范围内,所以此三角形的第三边长可能为5cm.
故答案为:C.
8.解:∵ AD平分∠BAC,
∴∠DAC=∠DAE.
∵∠C=90°, DE⊥AB,
∴∠C=∠E=90°.
∵AD=AD,∠DAC=∠DAE,∠C=∠E=90°,
∴△DAC≌△DAE,
∴∠CDA=∠EDA,
∴① AD平分∠CDE ,正确.
无法证明∠BDE=60°,
∴③ DE平分∠ADB错误.
∵BE+AE=AB,AE=AC,AC=4BE,
∴AB=5BE,AE=4BE,
∴S△ADB=5S△BDE , S△ADC=4S△BDE ,
∴S△ABC=9S△BDE , ④错误.
∵∠BDE=90°-∠B,∠BAC=90°-∠B,
∴∠BDE=∠BAC,
∴②∠BAC=∠BDE正确.
故答案为:B.
9.解:
∵ AC:BC:AB=5:12:13 ,
∵AD是 △ABC 的角平分线, DE⊥AB ,
∴∠CAD=∠BAD,∠C=∠AED =90°,
∵AD=AD,
∴ △ACD?△AED ,
∴ S△ACD=S△AED ,AE=AC=5k,
∴BE=13k-5k=8k,
∵ △AED 和 △BED 同高,
∴ S△BED:S△AED=8:5 ,
∵ △ABC 的面积为S,
∴ S△ACD=518S .
故答案为:B.
10.解:对图形进行点标注,如图所示:
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB.
∵∠ABC+∠ACB+∠A=180°,
∴2∠OBC+2∠OBC+∠A=180°,
∴∠OCB+∠OBC=90°-12∠A.
∵∠OCB+∠OBC+∠BOC=180°,
∴90°-12∠A+∠BOC=180°,
∴∠BOC=90°+12∠A.
而∠BOC=120°,
∴∠A=60°.
∵∠DCF=∠D+∠DBC,∠ACF=∠ABC+∠A,BD平分∠ABC,DC平分∠ACF,
∴∠ACF=2∠DCF,∠ABC=2∠DBC,
∴2∠D+2∠DBC=∠ABC+∠A,
∴2∠D=∠A,即∠D=12∠A.
∵∠A=60°,
∴∠D=30°.
故答案为:D.
二、填空题
11.解:∵∠3=∠1+∠2,∠1=∠2,∠3=120°,
∴ ∠1=12∠3=60° ,
故答案为:60°.
12.解:∵D为AC的中点
∴ AD=CD
∵CF∥AB
∴ ∠AED=∠F,∠A=∠FCD
在 △AED 和 △CFD 中{AD=CD∠AED=∠F∠A=∠FCD
∴ △AED≌△CFD (AAS)
∴ AE=CF
∵AB=15cm,CF=10cm,
BE=AB-AE=AB-CF=15-10=5cm
故答案为:5.
13.解:由作图步骤可知:AP为∠CAB的角平分线.
过点D作DE⊥AB于点E,则CD=DE=6.
∵DE=6,AB=20,
∴△ABD的面积=12×DE×AB=12×6×20=60.
故答案为:60.
14.解:∵∠A=52°,∴∠ABC+∠ACB=128°.
∵BD和CE是△ABC的两条角平分线,
∴∠1= 12 ∠ABC,∠2= 12 ∠ACB,
∴∠1+∠2= 12 (∠ABC+∠ACB)=64°.
故答案为:64°.
15.解:添加条件为∠A=∠D,理由是:
∵ ∠1=∠2 ,
∴∠ABC=∠DBE,
在△ABC和△DBE中,
{∠A=∠DAC=DE∠ABC=∠DBE ,
∴ △ABC≌△DBE (AAS),
故答案为:∠A=∠D.
16.解:如图所示:
∵AB∥CD,∠1=46°,
∴∠4=∠1=46°,
∵∠3=85°,
∴∠2=∠3-∠4=39°;
故答案为39.
17.解:过点A作AD⊥BC于点D,
∵EF 垂直平分BC,
∴当点P与EF和AC的交点重合时,BP=CP???
∴AP+BP=AC
两点之间线段最短,此时AP+BP的值最小,
∵S△ABC=12BC·AD=6
解之:AD=125
在Rt△ADC中,∠C=30°
∴AC=2AD=245.
故答案为:245.
18.解:∵ D、E、F分别为BC、AD、CE的中点, S△ABC=4cm2 ,
∴S△AEF=12S△ACE=12×12S△ACD=12×12×12S△ABC=18×4=12=0.5(cm2).
故答案为:0.5cm2.
三、解答题
19.解:情况一:题设①②③,结论④;
∵BF=EC,
∴ BF+CF=EC+CF ,
即 BC=EF ,
在△ABC和△DEF中,
{AB=DE∠B=∠EBC=EF ,
∴ △ABC?△DEF ,
∴ ∠1=∠2 ;
情况二:题设①③④,结论③;
在△ABC和△DEF中,
{∠1=∠2∠B=∠EAB=DE ,
∴ △ABC?△DEF ,
∴ BC=EF ,
∴ BC-FC=EF-FC ,即 BF=EC ;
情况三:题设②③④,结论①;
∵ BF=EC ,
∴ BF+CF=EC+CF ,
即 BC=EF ,
在△ABC和△DEF中,
{∠1=∠2BC=EF∠B=∠E ,
∴ △ABC?△DEF ,
∴ AB=DE ;
故答案为:①②③;④.
20. 证明: ∵CD//BE ,
∴∠ACD=∠B ,
在 △ACD 和 △CBE 中,
{∠ACD=∠BCD=BE∠D=∠E ,
∴△ACD ≌ △CBE(ASA) ,
∴AC=BC ,
则点C是线段AB的中点.
21. 证明:
∵ ∠BAD=∠CAE
∴ ∠BAD+∠BAC=∠CAE+∠BAC
即 ∠CAD=∠BAE
∴在 △ADC 与 △AEB 中
{AD=AE∠CAD=∠BAEAC=AB
∴ △ADC≌△AEB(SAS)
∴ ∠D=∠E
22. 等边对等角;垂直的定义;同位角相等,两直线平行;∠AGE;两直线平行,内错角相等;角平分线定义
求证:AD平分∠BAC,
证明:AF=AG(已知),
∴∠AGF=∠AFG(等边对等角),
∵AD⊥BC,GE⊥BC(已知) ,
∴∠ADC=∠GEC=90°(垂直的定义),
∴AD∥GE (同位角相等,两直线平行),
∴∠CAD=∠AGE(两直线平行,同位角相等)
∠BAD=∠AFG (两直线平行,内错角相等),
∴∠CAD=∠BAD(等量代换)
∴AD平分∠BAC (角平分线定义).
23. (1)解:如图,点D即为所求,
?(2)解:∵∠A=40°,∠C=90°,
∴∠ABC=90°-40°=50°,
∵BD平分∠ABC,
∴∠ABD=12∠ABC=25°,
∴∠ADB=180°-40°-25°=115°.
24. (1)证明:由题可知,
在△AOB与△COD中,
{AO=OC∠AOB=∠CODOB=OD ,
∵ΔAOB≌ΔCOD(SAS) ,
∴∠B=∠D ,
∴AB//CD ;
(2)OE=OF,理由如下:
由(1)可知: ΔAOB?ΔCOD ,
∴∠A=∠C,
在△AOE于△COF中,{∠A=∠CAO=CO∠AOE=∠COF
∴ΔAOE≌ΔCOF(ASA) ,
∴OE=OF .
25. (1)80;20
(2)解:20°
(3)解:20°
解:(1)∠BAC=180°-∠B-∠C=180°-30°-70°=80°;
∵AD平分∠BAC,
∴∠DAC=12∠BAC=40°,
∵AE⊥BC,
∴∠CAE=90°-∠C=90°-70°=20°,
∴∠DAE=∠DAC-∠CAE=40°-20°=20°.
(2)∵∠ADC=180°-∠C-∠DAC=180°-70°-40°=70°,
∴∠EDF=∠ADC=70°,
∵FE⊥BC,
∴∠DFE=90°-∠EDF=90°-70°=20°;
(3)∵∠B+∠BEA+∠BAE=180°,∠C+∠CEA+∠CAE=180°,
∵AE平分∠BEC,即∠BEA=∠CEA,
∴∠C-∠B=∠BAE-∠CAE=40°,
∴∠BAD+∠DAE-(∠CAD-∠DAE)=40°,
∵AE平分∠BAC,即∠BAD=∠CAD,
∴2∠DAE=40°,
∴∠DAE=20°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
