3. 7正多边形 同步练习（含解析）

中小学教育资源及组卷应用平台
浙教版九年级上
3.7正多边形同步练习
一．选择题
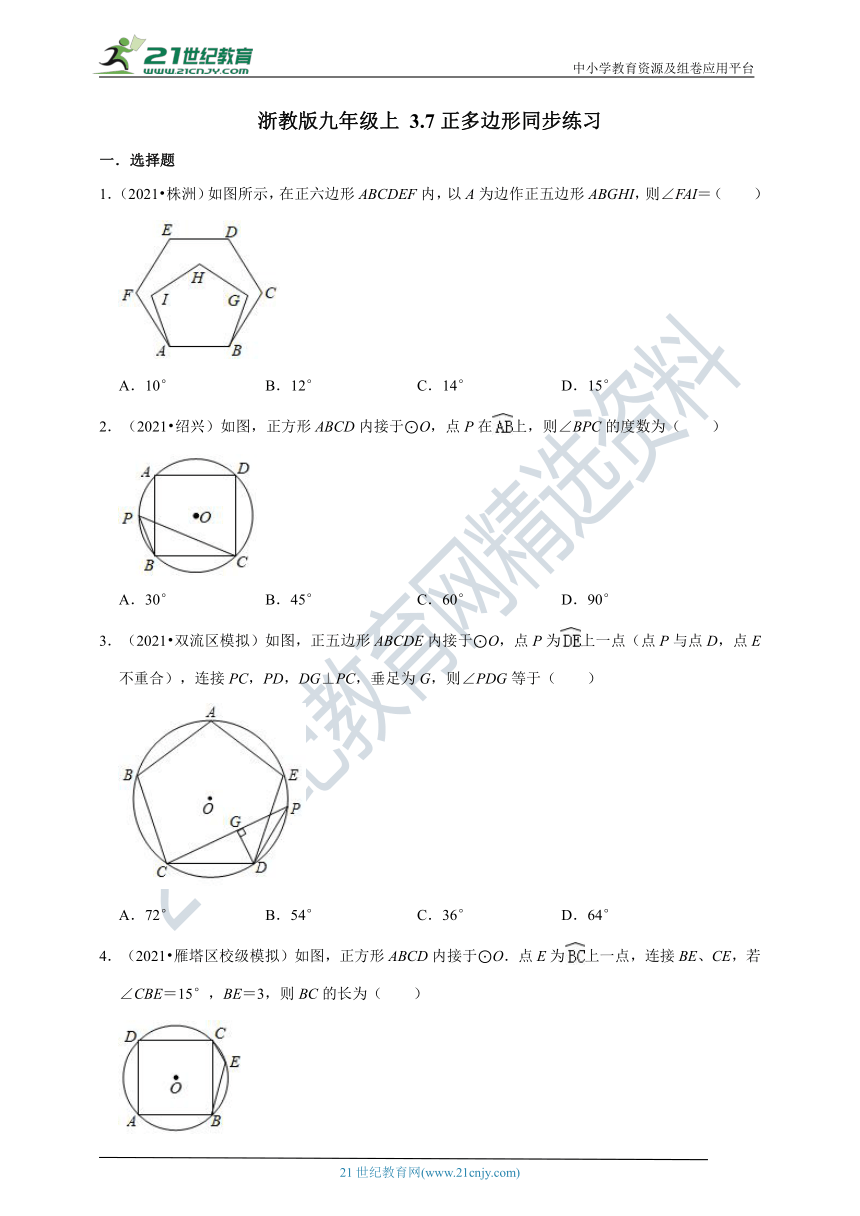
1．（2021?株洲）如图所示，在正六边形ABCDEF内，以A为边作正五边形ABGHI，则∠FAI＝（　　）
A．10°
B．12°
C．14°
D．15°
2．（2021?绍兴）如图，正方形ABCD内接于⊙O，点P在上，则∠BPC的度数为（　　）
A．30°
B．45°
C．60°
D．90°
3．（2021?双流区模拟）如图，正五边形ABCDE内接于⊙O，点P为上一点（点P与点D，点E不重合），连接PC，PD，DG⊥PC，垂足为G，则∠PDG等于（　　）
A．72°
B．54°
C．36°
D．64°
4．（2021?雁塔区校级模拟）如图，正方形ABCD内接于⊙O．点E为上一点，连接BE、CE，若∠CBE＝15°，BE＝3，则BC的长为（　　）
A．
B．
C．
D．
5．（2021?山西模拟）如图，在正五边形ABCDE中，连接AC，BE，BD，AC与BE，BD分别交于点F，G，若AB＝2，则FG的长为（　　）
A．3﹣
B．﹣1
C．
D．2﹣3
6．（2020秋?兴隆台区期末）如图，AB，BC和AC分别为⊙O内接正方形，正六边形和正n边形的一边，则n是（　　）
A．六
B．八
C．十
D．十二
7．（2020秋?东丽区期末）半径为3的正六边形的周长为（　　）
A．18
B．
C．
D．
8．（2020秋?余姚市期末）一个圆的内接正六边形与内接正方形的边长之比为（　　）
A．3：2
B．1：
C．1：
D．：
二．填空题
9．（2021?金山区二模）已知在正六边形ABCDEF中，AB＝6，那么正六边形ABCDEF的面积等于　
　．
10．（2021?碑林区校级模拟）如图，若正六边形ABCDEF边长为2，G为DE中点，连接对角线BG，则线段BG的长为　
　．
11．（2021?碑林区校级模拟）如图，在边长为6cm的正六边形中，点P在边AB上，连接PD、PE．则△PDE的面积为　
　cm2．
12．（2021?建邺区一模）如图，AD是正五边形ABCDE的一条对角线，以C为圆心，CB为半径画弧交AD于点F，连接CF，则∠CFD＝　
　°．
13．（2021?奉贤区二模）如图，⊙O的半径为6，如果弦AB是⊙O内接正方形的一边，弦AC是⊙O内接正十二边形的一边，那么弦BC的长为　
　．
三．解答题
14．（2021?武汉模拟）如图，正方形ABCD内接于⊙O，E是的中点，连接AE，DE，CE．
（1）求证：AE＝DE；
（2）若CE＝1，求四边形AECD的面积．
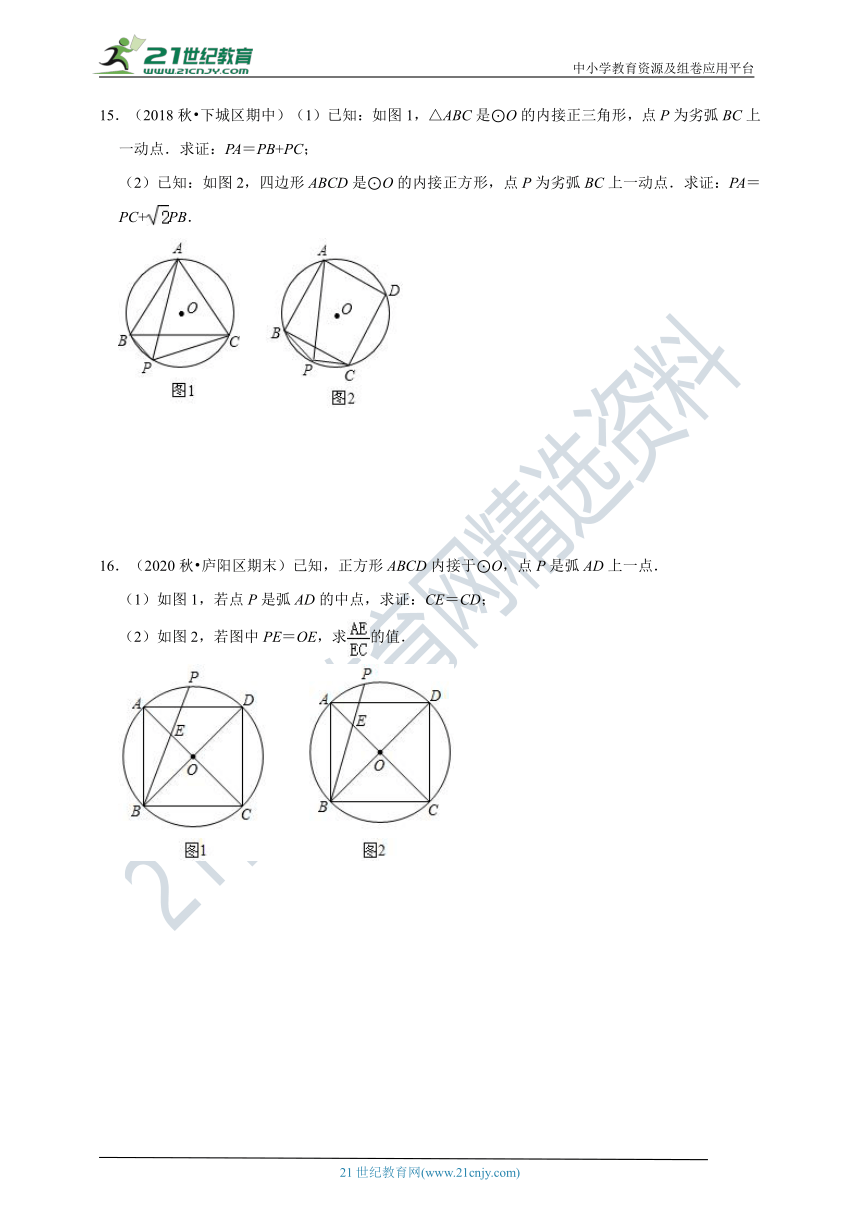
15．（2018秋?下城区期中）（1）已知：如图1，△ABC是⊙O的内接正三角形，点P为劣弧BC上一动点．求证：PA＝PB+PC；
（2）已知：如图2，四边形ABCD是⊙O的内接正方形，点P为劣弧BC上一动点．求证：PA＝PC+PB．
16．（2020秋?庐阳区期末）已知，正方形ABCD内接于⊙O，点P是弧AD上一点．
（1）如图1，若点P是弧AD的中点，求证：CE＝CD；
（2）如图2，若图中PE＝OE，求的值．
答案与解析
一．选择题（共8小题）
1．（2021?株洲）如图所示，在正六边形ABCDEF内，以A为边作正五边形ABGHI，则∠FAI＝（　　）
A．10°
B．12°
C．14°
D．15°
【解析】解：在正六边形ABCDEF内，正五边形ABGHI中，∠FAB＝120°,∠IAB＝108°,
∴∠FAI＝∠FAB﹣∠IAB＝120°﹣108°＝12°,
故选：B．
2．（2021?绍兴）如图，正方形ABCD内接于⊙O，点P在上，则∠BPC的度数为（　　）
A．30°
B．45°
C．60°
D．90°
【解析】解：连接OB、OC，如图，
∵正方形ABCD内接于⊙O，
∴BC弧所对的圆心角为90°，
∴∠BOC＝90°，
∴∠BPC＝∠BOC＝45°．
故选：B．
3．（2021?双流区模拟）如图，正五边形ABCDE内接于⊙O，点P为上一点（点P与点D，点E不重合），连接PC，PD，DG⊥PC，垂足为G，则∠PDG等于（　　）
A．72°
B．54°
C．36°
D．64°
【解析】解：连接OC，OD．
在正五边形ABCDE中，∠COD＝＝72°，
∴∠CPD＝∠COD＝36°，
∵DG⊥PC，
∴∠PGD＝90°，
∴∠PDG＝90°﹣36°＝54°，
故选：B．
4．（2021?雁塔区校级模拟）如图，正方形ABCD内接于⊙O．点E为上一点，连接BE、CE，若∠CBE＝15°，BE＝3，则BC的长为（　　）
A．
B．
C．
D．
【解析】解：连接OA，OB，OE，
∵正方形ABCD内接于⊙O，
∴OA＝OB＝OE，∠AOB＝＝90°，AB＝BC，∠ABC＝90°，
∴∠OAB＝∠OBA＝（180°﹣∠AOB）＝45°，
∴∠OBC＝∠ABC﹣∠OBA＝45°，
∵∠CBE＝15°，
∴∠OBE＝∠OBC+∠CBE＝60°，
∴△OBE是等边三角形，
∴OB＝BE＝3，
∴OA＝3，
∴AB＝＝3，
∴BC＝3，
故选：D．
5．（2021?山西模拟）如图，在正五边形ABCDE中，连接AC，BE，BD，AC与BE，BD分别交于点F，G，若AB＝2，则FG的长为（　　）
A．3﹣
B．﹣1
C．
D．2﹣3
【解析】解：∵五边形ABCDE是正五边形，
∴∠BAF＝∠ABF＝∠DBE＝36°，
∴FA＝FB，
∴∠ABG＝∠AGB＝∠BFG＝72°，
∴AB＝AG＝2，BG＝BF，
设AF＝BF＝BG＝x，
∵∠BGF＝∠AGB，∠GBF＝∠GAB，
∴△BGF∽△AGB，
∴BG2＝GF?GA，
∴x2＝（2﹣x）×2，
∴x2+2x﹣4＝0，
∴x＝﹣1+或﹣1﹣（舍弃），
∴FG＝AG﹣AF＝2﹣（﹣1+）＝3﹣，
故选：A．
6．（2020秋?兴隆台区期末）如图，AB，BC和AC分别为⊙O内接正方形，正六边形和正n边形的一边，则n是（　　）
A．六
B．八
C．十
D．十二
【解析】解：连接OA，OB，OC．
由题意，∠AOB＝＝90°，∠BOC＝＝60°，
∴∠AOC＝∠AOB﹣∠BOC＝30°，
∴n＝＝12，
故选：D．
7．（2020秋?东丽区期末）半径为3的正六边形的周长为（　　）
A．18
B．
C．
D．
【解析】解：∵正六边形的半径等于边长，
∴正六边形的边长a＝3，
正六边形的周长l＝6a＝18，
故选：A．
8．（2020秋?余姚市期末）一个圆的内接正六边形与内接正方形的边长之比为（　　）
A．3：2
B．1：
C．1：
D．：
【解析】解：设此圆的半径为R，
它的内接正六边形的边长为R，
则它的内接正方形的边长为R，
内接正六边形和内接四边形的边长比为R：R＝1：．
故选：C．
二．填空题
9．（2021?金山区二模）已知在正六边形ABCDEF中，AB＝6，那么正六边形ABCDEF的面积等于　54　．
【解析】解：连接OE、OD，如图所示：
∵六边形ABCDEF是正六边形，
∴∠DEF＝120°，
∴∠OED＝60°，
∵OE＝OD＝6，
∴△ODE是等边三角形，
作OH⊥ED于H，则OH＝OE?sin∠OED＝6×＝3，
∴S△ODE＝DE?OH＝×6×3＝9，
∴S正六边形ABCDEF＝6S△ODE＝54．
故答案为：54．
10．（2021?碑林区校级模拟）如图，若正六边形ABCDEF边长为2，G为DE中点，连接对角线BG，则线段BG的长为　　．
【解析】解：连接BE，过A作AM⊥BE于M，过F作FN⊥BE于N，过G作GH⊥BE于H，
则AF∥BE，
∴四边形AMNF是矩形，
∴MN＝AF＝2，∠FAM＝90°，
∵∠BAF＝＝120°，
∴∠BAM＝30°，
∴BM＝AB＝1，
同理：EN＝1，
∴BE＝4，EH＝，GH＝，
∴BH＝BE﹣EH＝4﹣＝，
∴BG＝＝＝，
方法二：连接BD，
∵正六边形ABCDEF边长为2，G为DE中点，
∴BC＝CD＝2，DG＝DE＝1，∠C＝∠CDG＝120°，
∴∠CDB＝30°，
∴∠BDG＝90°，
过C作CH⊥BD于H，
∴∠CHD＝90°，
∴DH＝CD＝，
∴BD＝2，
∴BG＝＝，
故答案为：．
11．（2021?碑林区校级模拟）如图，在边长为6cm的正六边形中，点P在边AB上，连接PD、PE．则△PDE的面积为　18　cm2．
【解析】解：如图所示，连接OD、OE，
此正六边形中DE＝6，
则∠DOE＝60°；
∵OD＝OE，
∴△ODE是等边三角形，
∵OG⊥DE，
∴∠DOG＝30°，
∴OG＝OD?cos30°＝6×＝3（cm），
∴△PDE边DE上的高为2OG＝6（cm），
∴S△PDE＝×6×6＝18（cm2），
故答案为18．
12．（2021?建邺区一模）如图，AD是正五边形ABCDE的一条对角线，以C为圆心，CB为半径画弧交AD于点F，连接CF，则∠CFD＝　72　°．
【解析】解：∵五边形ABCDE是正五边形，
∴∠CDE＝∠E＝＝108°，AE＝DE，
∴∠EDA＝∠EAD＝（180°﹣∠E）＝54°，
∴∠CDF＝∠CDE﹣∠EDA＝108°﹣36°＝72°，
∵CF＝CD，
∴∠CFD＝∠CDF＝72°，
故答案为：72．
13．（2021?奉贤区二模）如图，⊙O的半径为6，如果弦AB是⊙O内接正方形的一边，弦AC是⊙O内接正十二边形的一边，那么弦BC的长为　6　．
【解析】解：连接OA、OB、OC，作OD⊥BC于点D，
∵AB是⊙O内接正方形的一边，弦AC是⊙O内接正十二边形的一边，
∴∠AOB＝＝90°，∠AOC＝＝30°，
∴∠BOC＝∠AOB+∠AOC＝90°+30°＝120°，
∵OC＝OB，
∴∠OCD＝∠OBC＝30°，
∵OC＝6，
∴CD＝OCcos30°＝3，
∴BC＝2CD＝6，
故答案为：6．
三．解答题
14．（2021?武汉模拟）如图，正方形ABCD内接于⊙O，E是的中点，连接AE，DE，CE．
（1）求证：AE＝DE；
（2）若CE＝1，求四边形AECD的面积．
【解析】（1）证明：∵四边形ABCD是正方形，
∴AB＝CD，
∴＝，
∵E是的中点，
∴＝，
∴＝，
∴AE＝DE．
（2）解：连接BD，过点D作DF⊥DE交EC的延长线于F．
∵四边形ABCD是正方形，
∴∠DBC＝∠DEC＝45°，DA＝DC，
∵∠EDF＝90°，
∴∠F＝90°﹣45°＝45°，
∴DE＝DF，
∵∠ADC＝∠EDF＝90°，
∴∠ADE＝∠CDF，
在△ADE和△CDF中，
，
∴△ADE≌△CDF（AAS），
∴AE＝CF，
∴S△ADE＝S△CDF，
∴S四边形AECD＝S△DEF，
∵EF＝DE＝EC+DE，EC＝1，
∴1+DE＝DE，
∴DE＝+1，
∴S△DEF＝DE2＝+．
15．（2018秋?下城区期中）（1）已知：如图1，△ABC是⊙O的内接正三角形，点P为劣弧BC上一动点．求证：PA＝PB+PC；
（2）已知：如图2，四边形ABCD是⊙O的内接正方形，点P为劣弧BC上一动点．求证：PA＝PC+PB．
【解析】证明：（1）延长BP至E，使PE＝PC，连接CE，如图1，
∵A、B、P、C四点共圆，
∴∠BAC+∠BPC＝180°，
∵∠BPC+∠EPC＝180°，
∴∠BAC＝∠CPE＝60°，
∵PE＝PC，
∴△PCE是等边三角形，
∴CE＝PC，∠E＝60°；
又∵∠BCE＝60°+∠BCP，∠ACP＝60°+∠BCP，
∴∠BCE＝∠ACP，
∵△ABC、△ECP为等边三角形，
∴CE＝PC，AC＝BC，
在△BEC和△APC中，
，
∴△BEC≌△APC（SAS），
∴PA＝BE＝PB+PC；
（2）过点B作BE⊥PB交PA于E，连接OA，OB．如图2，
∵∠1+∠2＝∠2+∠3＝90°
∴∠1＝∠3，
∵∠APB＝∠AOB＝45°，
∴BP＝BE，
∴PE＝PB，
在△ABE和△CBP中，
，
∴△ABE≌△CBP（SAS），
∴PC＝AE，
∴PA＝AE+PE＝PC+PB；
16．（2020秋?庐阳区期末）已知，正方形ABCD内接于⊙O，点P是弧AD上一点．
（1）如图1，若点P是弧AD的中点，求证：CE＝CD；
（2）如图2，若图中PE＝OE，求的值．
【解析】（1）证明：如图1，连接DE，
∵四边形ABCD是正方形，
∴AC⊥BD，OB＝OD＝OC，
∴EB＝ED，∠ODC＝∠OCD＝45°，
∴∠EBD＝∠EDB，
∵点P是弧AD的中点，
∴∠PBD＝∠ABD＝×∠AOD＝22.5°，
∴∠EDC＝45°+22.5°＝67.5°，
∴∠CED＝180°﹣45°﹣67.5°＝67.5°，
∴∠CED＝∠EDC，
∴CE＝CD；
（2）解：如图2，连接DE，DP，
∵四边形ABCD是正方形，
∴∠BAD＝∠EOD＝90°，OA＝OD，
∴∠P＝∠BAD＝90°，
∵PE＝OE，
∴∠PDE＝∠2，由（1）知∠1＝∠2，
∴∠1＝∠2＝∠PDE，
∴∠1+∠2+∠PDE＝90°，
∴∠2＝30°，
∴OE＝DE，
∴DE＝2OE，
∴OD＝＝OE，
∴＝，
∴OD＝OA＝OE，
∴AE＝OA﹣OE＝（﹣1）OE，EC＝OE+OC＝（+1）OE，
∴＝＝2﹣．
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)