3.8 弧长及扇形的面积 同步练习(含解析)
文档属性
| 名称 | 3.8 弧长及扇形的面积 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 21:20:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级上
3.8弧长及扇形的面积同步练习
一.选择题
1.(2021?衢州)已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π
B.3π
C.5π
D.15π
2.(2021?平房区三模)一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为( )
A.30°
B.40°
C.80°
D.120°
3.(2021?南岗区校级一模)某扇形的圆心角为150°,其弧长为20πcm,则此扇形的面积是( )
A.120πcm
B.480πcm2
C.240πcm2
D.240cm2
4.(2021?连云港二模)如图,一扇形纸扇完全打开后,两竹条外侧OA和OB的夹角为120°,OA长为10cm,贴纸部分的CA长为5cm,则贴纸部分的面积为( )
A.cm2
B.25πcm2
C.48πcm2
D.75πcm2
5.(2021?德城区二模)一个滑轮起重装置如图所示,滑轮的半径是10cm,OA是滑轮的一条半径,当OA绕轴心O按逆时针方向旋转180°时,重物上升的高度为( )
A.10cm
B.10πcm
C.5cm
D.5πcm
6.(2021?上城区校级一模)如图,在矩形ABCD中,AB=3,BC=2,以点A为圆心,AD长为半径画弧交边BC于点E,连接AE,则的长为( )
A.π
B.π
C.π
D.π
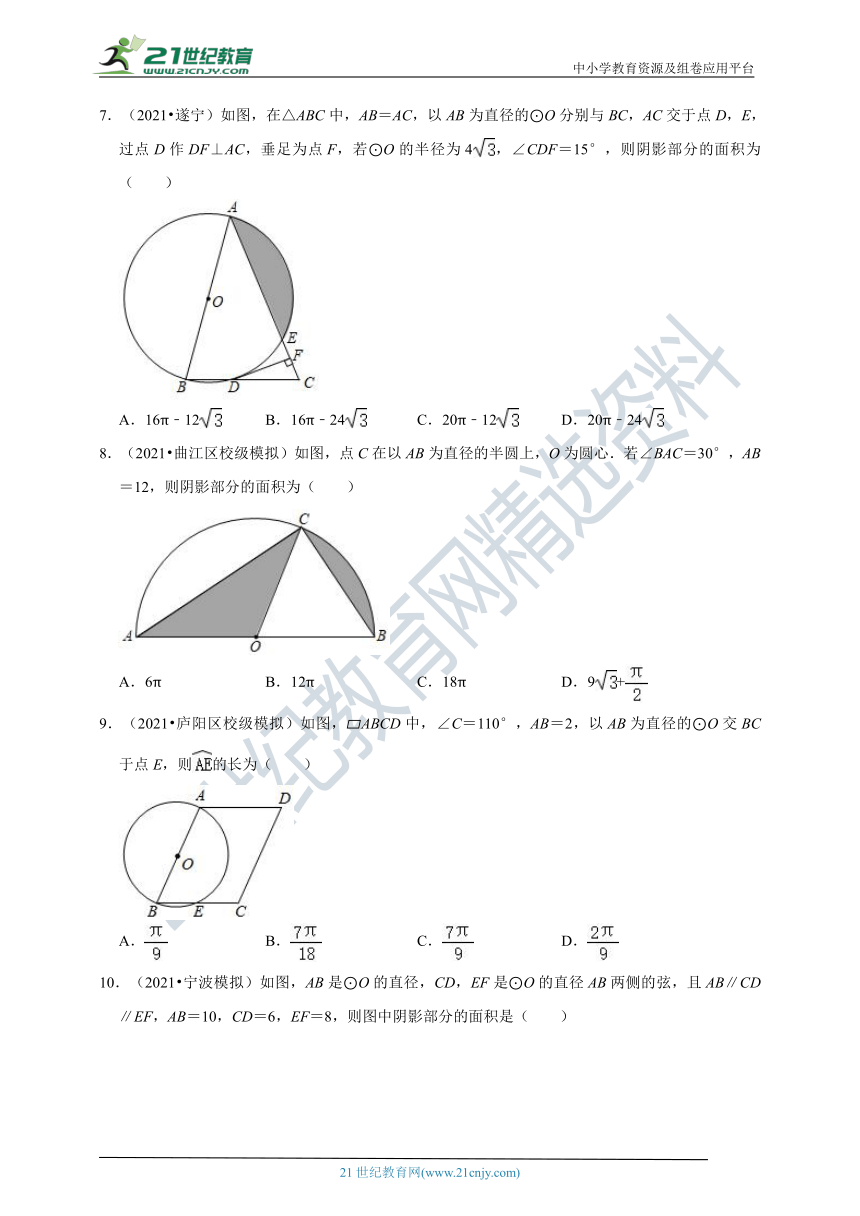
7.(2021?遂宁)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为4,∠CDF=15°,则阴影部分的面积为( )
A.16π﹣12
B.16π﹣24
C.20π﹣12
D.20π﹣24
8.(2021?曲江区校级模拟)如图,点C在以AB为直径的半圆上,O为圆心.若∠BAC=30°,AB=12,则阴影部分的面积为( )
A.6π
B.12π
C.18π
D.9+
9.(2021?庐阳区校级模拟)如图,?ABCD中,∠C=110°,AB=2,以AB为直径的⊙O交BC于点E,则的长为( )
A.
B.
C.
D.
10.(2021?宁波模拟)如图,AB是⊙O的直径,CD,EF是⊙O的直径AB两侧的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是( )
A.π
B.10π
C.24+4π
D.24+5π
二.填空题
11.(2021?南岗区校级二模)一个扇形的弧长是6πcm,面积是15πcm2,则此扇形的圆心角为
度.
12.(2021?道外区三模)某扇形的圆心角为45°,面积为9π,该扇形的弧长为
.
13.(2021?龙湾区二模)如图是一个由三条等弧围成的莱洛三角形,其中的圆心为点A,∠BAC=60°.若AB=1cm,则该莱洛三角形的周长是
cm.
14.(2021?铁锋区一模)如图,CD是以AB为直径的⊙O的一条弦,CD∥AB,∠CAD=40°,若⊙O的半径为9cm,则阴影部分的面积为
cm2.
15.(2021?凉山州)如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,BC=2,则线段AB扫过的图形(阴影部分)的面积为
.
16.(2021?碑林区校级模拟)如图Rt△ABC中,∠ACB=90°,BC=AC,将Rt△ABC绕点A逆时针旋转45°后,到Rt△AED,点B经过的路径为弧BE,已知AC=2,则图中阴影部分的面积为
.
三.解答题
17.(2021春?瓯海区月考)如图,∠EAD是⊙O内接四边形ABCD的一个外角,且∠EAD=75°,DB=DC.
(1)求∠BDC的度数.
(2)若⊙O的半径为2,求的长.
18.(2021?海陵区一模)已知:如图,在⊙O中,弦AB与CD相交于点E,∠ACD=60°,给出下列信息:
①∠ADC=50°;②AB是⊙O的直径;③∠CEB=100°.
(1)请在上述3条信息中选择其中两条作为条件,剩下的一条作为结论.你选择的条件是
,结论是
(只要填写序号).判断此命题是否正确,并说明理由;
(2)在(1)的情况下,若AD=2,求的长度.
19.(2019秋?青龙县期末)如图,⊙O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长.
(2)若点E为OC的中点,
①求劣弧CD的长度;
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
20.(2020春?朝阳区校级月考)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD、AC于点F、G.
(1)证明:FA=FB;
(2)若BD=DO=2,求的长度.
21.(2020秋?东莞市期末)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠ABC=30°,求图中阴影部分的面积.
22.(2020秋?海曙区校级期中)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
(1)求∠EBC的大小;
(2)若⊙O的半径为2.求图中阴影部分的面积.
答案与解析
一.选择题
1.(2021?衢州)已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π
B.3π
C.5π
D.15π
【解析】解:扇形面积=,
故选:D.
2.(2021?平房区三模)一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为( )
A.30°
B.40°
C.80°
D.120°
【解析】解:设扇形的圆心角是n°,
根据题意可知:S==π,
解得n=40°,
故选:B.
3.(2021?南岗区校级一模)某扇形的圆心角为150°,其弧长为20πcm,则此扇形的面积是( )
A.120πcm
B.480πcm2
C.240πcm2
D.240cm2
【解析】解:设扇形的半径为rcm,
∵扇形的圆心角为150°,它所对应的弧长为20πcm,
∴=20π,解得r=24
cm,
∴S扇形=×20π×24=240πcm2.
故选:C.
4.(2021?连云港二模)如图,一扇形纸扇完全打开后,两竹条外侧OA和OB的夹角为120°,OA长为10cm,贴纸部分的CA长为5cm,则贴纸部分的面积为( )
A.cm2
B.25πcm2
C.48πcm2
D.75πcm2
【解析】解:S=S扇形OAB﹣S扇形OCD=﹣=25π(cm2),
故选:B.
5.(2021?德城区二模)一个滑轮起重装置如图所示,滑轮的半径是10cm,OA是滑轮的一条半径,当OA绕轴心O按逆时针方向旋转180°时,重物上升的高度为( )
A.10cm
B.10πcm
C.5cm
D.5πcm
【解析】解:根据题意得,重物上升的高度==10π(cm).
故选:B.
6.(2021?上城区校级一模)如图,在矩形ABCD中,AB=3,BC=2,以点A为圆心,AD长为半径画弧交边BC于点E,连接AE,则的长为( )
A.π
B.π
C.π
D.π
【解析】解:由题意可知:AE=AD=BC=2,
在Rt△ABE中,sin∠AEB===,
∴∠AEB=60°,
∵AD∥BC,
∴∠AEB=∠DAE=60°,
l===,
故A、B、D错误,
故选:C.
7.(2021?遂宁)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为4,∠CDF=15°,则阴影部分的面积为( )
A.16π﹣12
B.16π﹣24
C.20π﹣12
D.20π﹣24
【解析】解:连接AD,OE
∵AB为直径,
∴∠ADB=∠ADC=90°,
∴∠ADF+∠CDF=90°,
∵DF⊥AC,
∴∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠CDF=∠DAC,
∵∠CDF=15°,
∴∠DAC=15°,
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=30°,
∵OA=OE,
∴∠OAE=∠OEA=30°,
∴∠AOE=120°,
作OH⊥AE于H,
在Rt△AOH中,OA=4,
∴OH=sin30°×OA=2,
AH=cos30°×OA=6,
∴AE=2AH=12,
∴S阴影=S扇形OAE﹣S△AOE==16.
故选:A.
8.(2021?曲江区校级模拟)如图,点C在以AB为直径的半圆上,O为圆心.若∠BAC=30°,AB=12,则阴影部分的面积为( )
A.6π
B.12π
C.18π
D.9+
【解析】解:∵直径AB=12,点C在半圆上,∠BAC=30°,
∴OA=OB=6,∠ACB=90°,∠COB=60°,
∴S△AOC=S△BOC,
∴阴影部分的面积=S扇形BCO==6π,
故选:A.
9.(2021?庐阳区校级模拟)如图,?ABCD中,∠C=110°,AB=2,以AB为直径的⊙O交BC于点E,则的长为( )
A.
B.
C.
D.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=110°,
∴∠B=70°,
∵OB=OE,
∴∠B=∠OEB,
∴∠OEB=70°,
∴∠AOE=∠B+∠OEB=70°+70°=140°,
∵AB=2,AB为⊙O的直径,
∴OA=OB=OE=1,
∴的长为:=,
故选:C.
10.(2021?宁波模拟)如图,AB是⊙O的直径,CD,EF是⊙O的直径AB两侧的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是( )
A.π
B.10π
C.24+4π
D.24+5π
【解析】解:连接OC、OD、OE、OF,作直径CM,连接DM,如图,
∵AB∥CD∥EF,
∴S△ACD=S△OCD,S△AEF=S△OEF,
∴图中阴影部分的面积=S扇形COD+S扇形EOF,
∵CM为直径,
∴∠CDM=90°,
∴DM==8,
∵EF=8,
∴DM=EF,
∴S扇形EOF=S扇形DOM,
∴图中阴影部分的面积=S扇形COD+S扇形DOM
=S半圆CM
=
=π.
故选:A.
二.填空题
11.(2021?南岗区校级二模)一个扇形的弧长是6πcm,面积是15πcm2,则此扇形的圆心角为
216 度.
【解析】解:∵一个扇形的弧长是6πcm,面积是15πcm2,S=lr,
∴15π=×6πr,
解得r=5,
∵l=,
∴6π=,
解得n=216,
即该扇形的圆心角为216°,
故答案为:216.
12.(2021?道外区三模)某扇形的圆心角为45°,面积为9π,该扇形的弧长为
π .
【解析】解:∵扇形的圆心角为45°,面积为
9π,
∴9π=,
∴r=6,
∵l=,
∴l==π,
故答案为π.
13.(2021?龙湾区二模)如图是一个由三条等弧围成的莱洛三角形,其中的圆心为点A,∠BAC=60°.若AB=1cm,则该莱洛三角形的周长是 π cm.
【解析】解:图中所在的圆的半径AB=1cm,相应的圆心角的度数为60°,
∴的长为=(cm),
∴该莱洛三角形的周长是×3=π(cm),
故答案为:π.
14.(2021?铁锋区一模)如图,CD是以AB为直径的⊙O的一条弦,CD∥AB,∠CAD=40°,若⊙O的半径为9cm,则阴影部分的面积为 18π cm2.
【解析】解:连接OC,OD,
∵∠CAD=40°,
∴∠COD=80°,
∵AB∥CD,
∴△ACD的面积=△COD的面积,
∴阴影部分的面积=扇形OCD的面积==18π.
故答案为:18π.
15.(2021?凉山州)如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,BC=2,则线段AB扫过的图形(阴影部分)的面积为 .
【解析】解:∵△ABC绕点C旋转60°得到△A′B′C,
∴△ABC≌△A′B′C,
∴S△ABC=S△A′B′C,∠BCB′=∠ACA′=120°.
∵AB扫过的图形的面积=S扇形ACA′+S△ABC﹣S扇形BCB′﹣S△A′B′C,
∴AB扫过的图形的面积=S扇形ACA′﹣S扇形BCB′,
∴AB扫过的图形的面积=﹣=.
故答案为:。
16.(2021?碑林区校级模拟)如图Rt△ABC中,∠ACB=90°,BC=AC,将Rt△ABC绕点A逆时针旋转45°后,到Rt△AED,点B经过的路径为弧BE,已知AC=2,则图中阴影部分的面积为 2π .
【解析】解:在Rt△ABC中,∠ACB=90°,BC=AC,
∴tan∠BAC==,
∴∠CAB=60°,
∴∠ABC=30°
∴AB=2AC=2×2=4,
由题意得,△ACB≌△ADE,∠BAE=45°,
则图中阴影部分的面积=S△AED+S扇形EAB﹣S△ACB=S扇形EAB==2π,
故答案为:2π.
三.解答题
17.(2021春?瓯海区月考)如图,∠EAD是⊙O内接四边形ABCD的一个外角,且∠EAD=75°,DB=DC.
(1)求∠BDC的度数.
(2)若⊙O的半径为2,求的长.
【解析】解:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠C=180°,
∵∠EAD+∠DAB=180°,
∴∠C=∠EAD,
∵∠EAD=75°,
∴∠C=75°,
∵DB=DC,
∴∠DBC=∠C=75°,
∴∠BDC=180°﹣∠C﹣∠DBC=30°;
(2)连接OB、OC,
∵∠BDC=30°,
∴∠BOC=2∠BDC=60°(圆周角定理),
∵⊙O的半径为2,
∴的长是=.
18.(2021?海陵区一模)已知:如图,在⊙O中,弦AB与CD相交于点E,∠ACD=60°,给出下列信息:
①∠ADC=50°;②AB是⊙O的直径;③∠CEB=100°.
(1)请在上述3条信息中选择其中两条作为条件,剩下的一条作为结论.你选择的条件是 ①② ,结论是 ③ (只要填写序号).判断此命题是否正确,并说明理由;
(2)在(1)的情况下,若AD=2,求的长度.
【解析】解:(1)条件为①②,结论为③,结论正确,理由如下:
连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ADC=50°=∠ABC,
∴∠BAC=90°﹣∠ABC=90°﹣50°=40°,
∴∠CEB=∠BAC+∠ACD=40°+60°=100°;
故答案为:①②,③;
(2)连接OD,BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠ABD=∠ACD=60°,AD=2,
∴AB===4,
∴OA=AB=2,
又∵∠AOD=2∠ABD=2×60°=120°,
∴的长度为=.
19.(2019秋?青龙县期末)如图,⊙O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长.
(2)若点E为OC的中点,
①求劣弧CD的长度;
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
【解析】解:(1)如图,连接OD,
∵⊙O的直径AB=16,
∴圆的半径为16÷2=8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴EF=OD=8.
(2)①∵点E为OC的中点,
∴,
∴∠EDO=30°,
∴∠DOE=60°,
∴劣弧CD的长度为.
②延长CO交⊙O于点G,连接DG交AB于点P,
则PC+PD的最小值为DG.
∵,,
∴,
∴PC+PD的最小值为.
20.(2020春?朝阳区校级月考)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD、AC于点F、G.
(1)证明:FA=FB;
(2)若BD=DO=2,求的长度.
【解析】(1)证明:∵BC
是⊙O
的直径,
∴∠BAC=90°,
∴∠ABE+∠AGB=90°;
∵AD⊥BC,
∴∠C+∠CAD=90°;
∵=,
∴∠C=∠ABE,
∴∠AGB=∠CAD,
∵∠C=∠BAD
∴∠BAD=∠ABE
∴FA=FB.
(2)解:如图,连接AO、EO,
,
∵BD=DO=2,AD⊥BC,
∴AB=AO,
∵AO=BO,
∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠AOB=60°,
∵=,
∴∠AOE=60°,
∴∠EOC=60°,
∴的长度==π.
21.(2020秋?东莞市期末)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠ABC=30°,求图中阴影部分的面积.
【解析】(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED,
(2)解:连接CD,OD,
∵OC=OB,
∴∠OCB=∠ABC=30°,
∴∠AOC=∠OCB+∠ABC=60°,
∵OC⊥AD,
∴=,
∴∠COD=∠AOC=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴OE==,
∴S阴影=S扇形AOD﹣S△AOD=﹣×=3π﹣.
22.(2020秋?海曙区校级期中)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
(1)求∠EBC的大小;
(2)若⊙O的半径为2.求图中阴影部分的面积.
【解析】解;(1)∵AB是⊙O的直径,
∴∠AEB=90°,
又∵∠BAC=45°,
∴∠ABE=45°.
又∵AB=AC,
∴∠ABC=∠C=67.5°.
∴∠EBC=22.5°;
(2)连接OE,
∵AB是⊙O的直径,
∴∠AEB=90°,
又∵∠BAC=45°,
∴∠ABE=45°.
∴AE=BE,
∵OA=OB,
∴OE⊥AB,
∵OA=OB=OE=2,
∴S阴影=S扇形OBE﹣S△OBE=﹣=﹣=π﹣2.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版九年级上
3.8弧长及扇形的面积同步练习
一.选择题
1.(2021?衢州)已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π
B.3π
C.5π
D.15π
2.(2021?平房区三模)一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为( )
A.30°
B.40°
C.80°
D.120°
3.(2021?南岗区校级一模)某扇形的圆心角为150°,其弧长为20πcm,则此扇形的面积是( )
A.120πcm
B.480πcm2
C.240πcm2
D.240cm2
4.(2021?连云港二模)如图,一扇形纸扇完全打开后,两竹条外侧OA和OB的夹角为120°,OA长为10cm,贴纸部分的CA长为5cm,则贴纸部分的面积为( )
A.cm2
B.25πcm2
C.48πcm2
D.75πcm2
5.(2021?德城区二模)一个滑轮起重装置如图所示,滑轮的半径是10cm,OA是滑轮的一条半径,当OA绕轴心O按逆时针方向旋转180°时,重物上升的高度为( )
A.10cm
B.10πcm
C.5cm
D.5πcm
6.(2021?上城区校级一模)如图,在矩形ABCD中,AB=3,BC=2,以点A为圆心,AD长为半径画弧交边BC于点E,连接AE,则的长为( )
A.π
B.π
C.π
D.π
7.(2021?遂宁)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为4,∠CDF=15°,则阴影部分的面积为( )
A.16π﹣12
B.16π﹣24
C.20π﹣12
D.20π﹣24
8.(2021?曲江区校级模拟)如图,点C在以AB为直径的半圆上,O为圆心.若∠BAC=30°,AB=12,则阴影部分的面积为( )
A.6π
B.12π
C.18π
D.9+
9.(2021?庐阳区校级模拟)如图,?ABCD中,∠C=110°,AB=2,以AB为直径的⊙O交BC于点E,则的长为( )
A.
B.
C.
D.
10.(2021?宁波模拟)如图,AB是⊙O的直径,CD,EF是⊙O的直径AB两侧的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是( )
A.π
B.10π
C.24+4π
D.24+5π
二.填空题
11.(2021?南岗区校级二模)一个扇形的弧长是6πcm,面积是15πcm2,则此扇形的圆心角为
度.
12.(2021?道外区三模)某扇形的圆心角为45°,面积为9π,该扇形的弧长为
.
13.(2021?龙湾区二模)如图是一个由三条等弧围成的莱洛三角形,其中的圆心为点A,∠BAC=60°.若AB=1cm,则该莱洛三角形的周长是
cm.
14.(2021?铁锋区一模)如图,CD是以AB为直径的⊙O的一条弦,CD∥AB,∠CAD=40°,若⊙O的半径为9cm,则阴影部分的面积为
cm2.
15.(2021?凉山州)如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,BC=2,则线段AB扫过的图形(阴影部分)的面积为
.
16.(2021?碑林区校级模拟)如图Rt△ABC中,∠ACB=90°,BC=AC,将Rt△ABC绕点A逆时针旋转45°后,到Rt△AED,点B经过的路径为弧BE,已知AC=2,则图中阴影部分的面积为
.
三.解答题
17.(2021春?瓯海区月考)如图,∠EAD是⊙O内接四边形ABCD的一个外角,且∠EAD=75°,DB=DC.
(1)求∠BDC的度数.
(2)若⊙O的半径为2,求的长.
18.(2021?海陵区一模)已知:如图,在⊙O中,弦AB与CD相交于点E,∠ACD=60°,给出下列信息:
①∠ADC=50°;②AB是⊙O的直径;③∠CEB=100°.
(1)请在上述3条信息中选择其中两条作为条件,剩下的一条作为结论.你选择的条件是
,结论是
(只要填写序号).判断此命题是否正确,并说明理由;
(2)在(1)的情况下,若AD=2,求的长度.
19.(2019秋?青龙县期末)如图,⊙O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长.
(2)若点E为OC的中点,
①求劣弧CD的长度;
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
20.(2020春?朝阳区校级月考)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD、AC于点F、G.
(1)证明:FA=FB;
(2)若BD=DO=2,求的长度.
21.(2020秋?东莞市期末)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠ABC=30°,求图中阴影部分的面积.
22.(2020秋?海曙区校级期中)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
(1)求∠EBC的大小;
(2)若⊙O的半径为2.求图中阴影部分的面积.
答案与解析
一.选择题
1.(2021?衢州)已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π
B.3π
C.5π
D.15π
【解析】解:扇形面积=,
故选:D.
2.(2021?平房区三模)一个扇形的半径为3cm,面积为πcm2,则此扇形的圆心角为( )
A.30°
B.40°
C.80°
D.120°
【解析】解:设扇形的圆心角是n°,
根据题意可知:S==π,
解得n=40°,
故选:B.
3.(2021?南岗区校级一模)某扇形的圆心角为150°,其弧长为20πcm,则此扇形的面积是( )
A.120πcm
B.480πcm2
C.240πcm2
D.240cm2
【解析】解:设扇形的半径为rcm,
∵扇形的圆心角为150°,它所对应的弧长为20πcm,
∴=20π,解得r=24
cm,
∴S扇形=×20π×24=240πcm2.
故选:C.
4.(2021?连云港二模)如图,一扇形纸扇完全打开后,两竹条外侧OA和OB的夹角为120°,OA长为10cm,贴纸部分的CA长为5cm,则贴纸部分的面积为( )
A.cm2
B.25πcm2
C.48πcm2
D.75πcm2
【解析】解:S=S扇形OAB﹣S扇形OCD=﹣=25π(cm2),
故选:B.
5.(2021?德城区二模)一个滑轮起重装置如图所示,滑轮的半径是10cm,OA是滑轮的一条半径,当OA绕轴心O按逆时针方向旋转180°时,重物上升的高度为( )
A.10cm
B.10πcm
C.5cm
D.5πcm
【解析】解:根据题意得,重物上升的高度==10π(cm).
故选:B.
6.(2021?上城区校级一模)如图,在矩形ABCD中,AB=3,BC=2,以点A为圆心,AD长为半径画弧交边BC于点E,连接AE,则的长为( )
A.π
B.π
C.π
D.π
【解析】解:由题意可知:AE=AD=BC=2,
在Rt△ABE中,sin∠AEB===,
∴∠AEB=60°,
∵AD∥BC,
∴∠AEB=∠DAE=60°,
l===,
故A、B、D错误,
故选:C.
7.(2021?遂宁)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为4,∠CDF=15°,则阴影部分的面积为( )
A.16π﹣12
B.16π﹣24
C.20π﹣12
D.20π﹣24
【解析】解:连接AD,OE
∵AB为直径,
∴∠ADB=∠ADC=90°,
∴∠ADF+∠CDF=90°,
∵DF⊥AC,
∴∠AFD=90°,
∴∠ADF+∠DAF=90°,
∴∠CDF=∠DAC,
∵∠CDF=15°,
∴∠DAC=15°,
∵AB=AC,AD⊥BC,
∴∠BAC=2∠DAC=30°,
∵OA=OE,
∴∠OAE=∠OEA=30°,
∴∠AOE=120°,
作OH⊥AE于H,
在Rt△AOH中,OA=4,
∴OH=sin30°×OA=2,
AH=cos30°×OA=6,
∴AE=2AH=12,
∴S阴影=S扇形OAE﹣S△AOE==16.
故选:A.
8.(2021?曲江区校级模拟)如图,点C在以AB为直径的半圆上,O为圆心.若∠BAC=30°,AB=12,则阴影部分的面积为( )
A.6π
B.12π
C.18π
D.9+
【解析】解:∵直径AB=12,点C在半圆上,∠BAC=30°,
∴OA=OB=6,∠ACB=90°,∠COB=60°,
∴S△AOC=S△BOC,
∴阴影部分的面积=S扇形BCO==6π,
故选:A.
9.(2021?庐阳区校级模拟)如图,?ABCD中,∠C=110°,AB=2,以AB为直径的⊙O交BC于点E,则的长为( )
A.
B.
C.
D.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=110°,
∴∠B=70°,
∵OB=OE,
∴∠B=∠OEB,
∴∠OEB=70°,
∴∠AOE=∠B+∠OEB=70°+70°=140°,
∵AB=2,AB为⊙O的直径,
∴OA=OB=OE=1,
∴的长为:=,
故选:C.
10.(2021?宁波模拟)如图,AB是⊙O的直径,CD,EF是⊙O的直径AB两侧的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是( )
A.π
B.10π
C.24+4π
D.24+5π
【解析】解:连接OC、OD、OE、OF,作直径CM,连接DM,如图,
∵AB∥CD∥EF,
∴S△ACD=S△OCD,S△AEF=S△OEF,
∴图中阴影部分的面积=S扇形COD+S扇形EOF,
∵CM为直径,
∴∠CDM=90°,
∴DM==8,
∵EF=8,
∴DM=EF,
∴S扇形EOF=S扇形DOM,
∴图中阴影部分的面积=S扇形COD+S扇形DOM
=S半圆CM
=
=π.
故选:A.
二.填空题
11.(2021?南岗区校级二模)一个扇形的弧长是6πcm,面积是15πcm2,则此扇形的圆心角为
216 度.
【解析】解:∵一个扇形的弧长是6πcm,面积是15πcm2,S=lr,
∴15π=×6πr,
解得r=5,
∵l=,
∴6π=,
解得n=216,
即该扇形的圆心角为216°,
故答案为:216.
12.(2021?道外区三模)某扇形的圆心角为45°,面积为9π,该扇形的弧长为
π .
【解析】解:∵扇形的圆心角为45°,面积为
9π,
∴9π=,
∴r=6,
∵l=,
∴l==π,
故答案为π.
13.(2021?龙湾区二模)如图是一个由三条等弧围成的莱洛三角形,其中的圆心为点A,∠BAC=60°.若AB=1cm,则该莱洛三角形的周长是 π cm.
【解析】解:图中所在的圆的半径AB=1cm,相应的圆心角的度数为60°,
∴的长为=(cm),
∴该莱洛三角形的周长是×3=π(cm),
故答案为:π.
14.(2021?铁锋区一模)如图,CD是以AB为直径的⊙O的一条弦,CD∥AB,∠CAD=40°,若⊙O的半径为9cm,则阴影部分的面积为 18π cm2.
【解析】解:连接OC,OD,
∵∠CAD=40°,
∴∠COD=80°,
∵AB∥CD,
∴△ACD的面积=△COD的面积,
∴阴影部分的面积=扇形OCD的面积==18π.
故答案为:18π.
15.(2021?凉山州)如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,BC=2,则线段AB扫过的图形(阴影部分)的面积为 .
【解析】解:∵△ABC绕点C旋转60°得到△A′B′C,
∴△ABC≌△A′B′C,
∴S△ABC=S△A′B′C,∠BCB′=∠ACA′=120°.
∵AB扫过的图形的面积=S扇形ACA′+S△ABC﹣S扇形BCB′﹣S△A′B′C,
∴AB扫过的图形的面积=S扇形ACA′﹣S扇形BCB′,
∴AB扫过的图形的面积=﹣=.
故答案为:。
16.(2021?碑林区校级模拟)如图Rt△ABC中,∠ACB=90°,BC=AC,将Rt△ABC绕点A逆时针旋转45°后,到Rt△AED,点B经过的路径为弧BE,已知AC=2,则图中阴影部分的面积为 2π .
【解析】解:在Rt△ABC中,∠ACB=90°,BC=AC,
∴tan∠BAC==,
∴∠CAB=60°,
∴∠ABC=30°
∴AB=2AC=2×2=4,
由题意得,△ACB≌△ADE,∠BAE=45°,
则图中阴影部分的面积=S△AED+S扇形EAB﹣S△ACB=S扇形EAB==2π,
故答案为:2π.
三.解答题
17.(2021春?瓯海区月考)如图,∠EAD是⊙O内接四边形ABCD的一个外角,且∠EAD=75°,DB=DC.
(1)求∠BDC的度数.
(2)若⊙O的半径为2,求的长.
【解析】解:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠C=180°,
∵∠EAD+∠DAB=180°,
∴∠C=∠EAD,
∵∠EAD=75°,
∴∠C=75°,
∵DB=DC,
∴∠DBC=∠C=75°,
∴∠BDC=180°﹣∠C﹣∠DBC=30°;
(2)连接OB、OC,
∵∠BDC=30°,
∴∠BOC=2∠BDC=60°(圆周角定理),
∵⊙O的半径为2,
∴的长是=.
18.(2021?海陵区一模)已知:如图,在⊙O中,弦AB与CD相交于点E,∠ACD=60°,给出下列信息:
①∠ADC=50°;②AB是⊙O的直径;③∠CEB=100°.
(1)请在上述3条信息中选择其中两条作为条件,剩下的一条作为结论.你选择的条件是 ①② ,结论是 ③ (只要填写序号).判断此命题是否正确,并说明理由;
(2)在(1)的情况下,若AD=2,求的长度.
【解析】解:(1)条件为①②,结论为③,结论正确,理由如下:
连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ADC=50°=∠ABC,
∴∠BAC=90°﹣∠ABC=90°﹣50°=40°,
∴∠CEB=∠BAC+∠ACD=40°+60°=100°;
故答案为:①②,③;
(2)连接OD,BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠ABD=∠ACD=60°,AD=2,
∴AB===4,
∴OA=AB=2,
又∵∠AOD=2∠ABD=2×60°=120°,
∴的长度为=.
19.(2019秋?青龙县期末)如图,⊙O的直径AB=16,半径OC⊥AB,D为上一动点(不包括B,C两点),DE⊥OC,DF⊥AB,垂足分别为E,F.
(1)求EF的长.
(2)若点E为OC的中点,
①求劣弧CD的长度;
②若点P为直径AB上一动点,直接写出PC+PD的最小值.
【解析】解:(1)如图,连接OD,
∵⊙O的直径AB=16,
∴圆的半径为16÷2=8.
∵OC⊥AB,DE⊥OC,DF⊥AB,
∴四边形OFDE是矩形,
∴EF=OD=8.
(2)①∵点E为OC的中点,
∴,
∴∠EDO=30°,
∴∠DOE=60°,
∴劣弧CD的长度为.
②延长CO交⊙O于点G,连接DG交AB于点P,
则PC+PD的最小值为DG.
∵,,
∴,
∴PC+PD的最小值为.
20.(2020春?朝阳区校级月考)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,=,BE分别交AD、AC于点F、G.
(1)证明:FA=FB;
(2)若BD=DO=2,求的长度.
【解析】(1)证明:∵BC
是⊙O
的直径,
∴∠BAC=90°,
∴∠ABE+∠AGB=90°;
∵AD⊥BC,
∴∠C+∠CAD=90°;
∵=,
∴∠C=∠ABE,
∴∠AGB=∠CAD,
∵∠C=∠BAD
∴∠BAD=∠ABE
∴FA=FB.
(2)解:如图,连接AO、EO,
,
∵BD=DO=2,AD⊥BC,
∴AB=AO,
∵AO=BO,
∴AB=AO=BO,
∴△ABO是等边三角形,
∴∠AOB=60°,
∵=,
∴∠AOE=60°,
∴∠EOC=60°,
∴的长度==π.
21.(2020秋?东莞市期末)如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.
(1)求证:AE=ED;
(2)若AB=6,∠ABC=30°,求图中阴影部分的面积.
【解析】(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED,
(2)解:连接CD,OD,
∵OC=OB,
∴∠OCB=∠ABC=30°,
∴∠AOC=∠OCB+∠ABC=60°,
∵OC⊥AD,
∴=,
∴∠COD=∠AOC=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴OE==,
∴S阴影=S扇形AOD﹣S△AOD=﹣×=3π﹣.
22.(2020秋?海曙区校级期中)已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
(1)求∠EBC的大小;
(2)若⊙O的半径为2.求图中阴影部分的面积.
【解析】解;(1)∵AB是⊙O的直径,
∴∠AEB=90°,
又∵∠BAC=45°,
∴∠ABE=45°.
又∵AB=AC,
∴∠ABC=∠C=67.5°.
∴∠EBC=22.5°;
(2)连接OE,
∵AB是⊙O的直径,
∴∠AEB=90°,
又∵∠BAC=45°,
∴∠ABE=45°.
∴AE=BE,
∵OA=OB,
∴OE⊥AB,
∵OA=OB=OE=2,
∴S阴影=S扇形OBE﹣S△OBE=﹣=﹣=π﹣2.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
