1.5 三角形全等的判定(第4课时) 同步练习 2021-2022学年浙教版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 1.5 三角形全等的判定(第4课时) 同步练习 2021-2022学年浙教版数学八年级上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 49.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览

文档简介
1.5 三角形全等的判定
【笔记】
1.全等三角形的判定:________及其中一个角的________对应相等的两个三角形全等(简写成“________”或“________”).
2.角平分线的性质:角平分线上的点到________的距离相等.
【训练】
31896053619501.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C
B.AD=CB
C.BE=DF 第1题图
D.AD∥BC
47136051314452.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( ) 第2题图
A.SAS B.ASA
C.AAS D.SSS
3.如图,已知在△ABC中,CD
是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
第3题图 第4题图
44754805791204.如图所示,已知∠1=∠2,AD=BC,AC,BD相交于点O,MN经过点O,则图中全等三角形的对数为( )
A.4对 B.5对 C.6对 D.7对
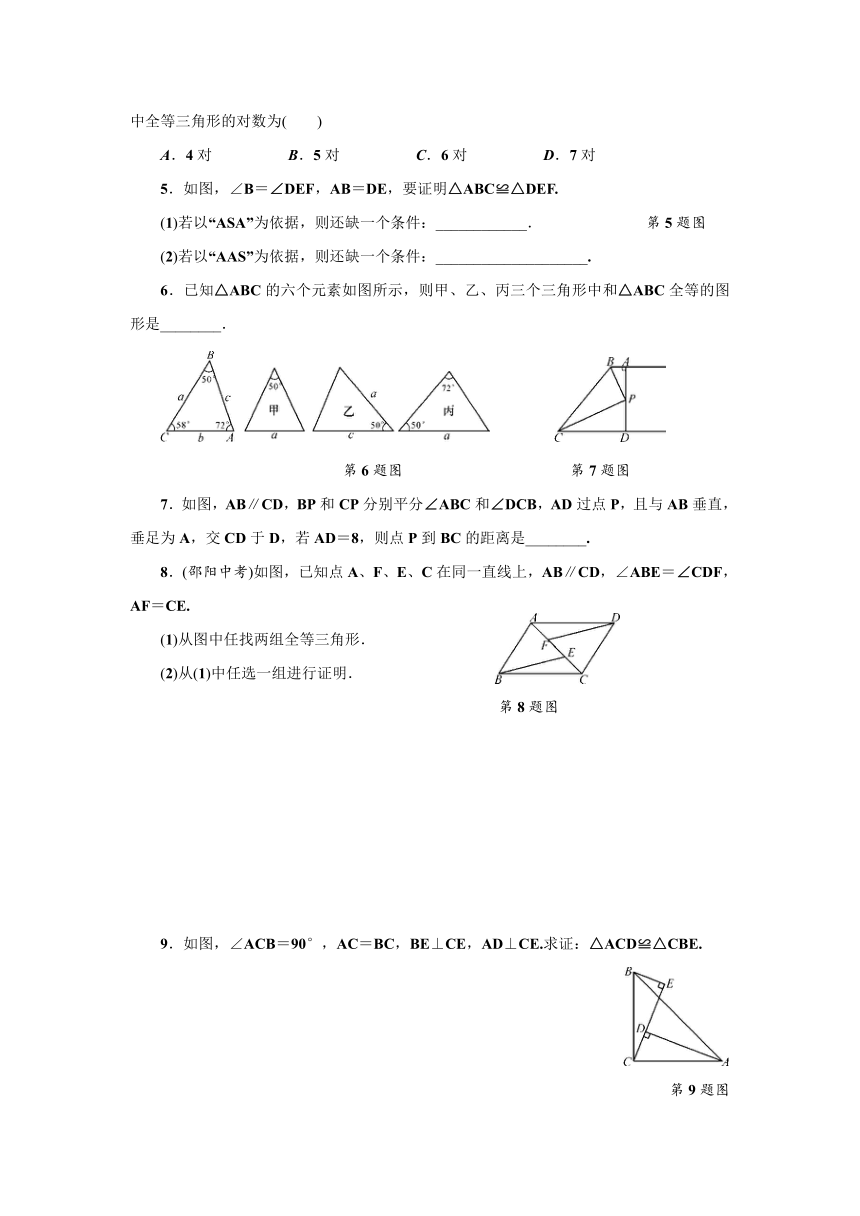
5.如图,∠B=∠DEF,AB=DE,要证明△ABC≌△DEF.
(1)若以“ASA”为依据,则还缺一个条件:____________. 第5题图
(2)若以“AAS”为依据,则还缺一个条件:____________________.
6.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中和△ABC全等的图形是________.
第6题图 第7题图
7.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,垂足为A,交CD于D,若AD=8,则点P到BC的距离是________.
32086555181608.(邵阳中考)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形.
(2)从(1)中任选一组进行证明.
第8题图
9.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.
第9题图
10.△ABC是格点三角形(顶点在网格线的交点),则图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是________个.
第10题图 第11题图
11.如图,在△ABC中,AD平分∠BAC,AB=6,AC=4.若△ABD的面积等于9,则△ACD的面积为________.
12.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.求证:
376110543815(1)△ABE≌△DCE.
(2)△ABC≌△DCB.
第12题图
13.如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,过点A作AE⊥l3于点E,求BE的长.
第13题图
386588026670014.如图,在四边形ABCD中,已知BD平分∠ABC,∠BAD+∠C=180°,求证:AD=CD.
第14题图
参考答案
1.5 三角形全等的判定(第4课时)
【笔记】
1.两角 对边 角角边 AAS
2.角两边
【训练】
1—4.BDCC
5.(1)∠A=∠D (2)∠ACB=∠F
6.乙、丙
7.4
8.(1)△ABE≌△CDF,△AFD≌△CEB(答案不唯一). (2)∵AB∥CD,∴∠1=∠2,∵AF=CE,∴AF+EF=CE+EF,即AE=FC,在△ABE和△CDF中,∴△ABE≌△CDF(AAS).
第8题图
9.∵BE⊥CE,AD⊥CE,∴∠CEB=∠ADC=90°,∵∠BCE+∠ACD=∠ACB=90°,∠CAD+∠ACD=180°-90°=90°,∴∠BCE=∠CAD,在△ACD和△CBE中,∴△CBE≌△ACD(AAS).
10.4
11.6
12.(1)在△ABE和△DCE中,∴△ABE≌△DCE(AAS). (2)∵△ABE≌△DCE,∴AE=DE,BE=CE,∴AC=DB.在△ABC和△DCB中,
∴△ABC≌△DCB(SAS).
13.过点C作CF⊥l3于点F.∵l1,l2之间的距离为1,l2,l3之间的距离为2,AE⊥l3,CF⊥l3,∴CF=3,∠AEB=∠BFC=90°.∴∠EAB+∠ABE=90°.∵∠ABC=90°,∴∠ABE+∠FBC=90°.∴∠EAB=∠FBC.在△AEB和△BFC中,∵∴△AEB≌△BFC(AAS).∴BE=CF=3.
第13题图 第14题图
14.过点D作DE⊥BA交BA的延长线于点E,过点D作DF⊥BC,垂足为F,∴∠AED=∠CFD=90°,∵BD平分∠ABC,∴DE=DF.∵∠BAD+∠C=180°,∠BAD+∠DAE=180°,∴∠DAE=∠C.在△AED和△CFD中,∴△AED≌△CFD(AAS),∴AD=CD.
【笔记】
1.全等三角形的判定:________及其中一个角的________对应相等的两个三角形全等(简写成“________”或“________”).
2.角平分线的性质:角平分线上的点到________的距离相等.
【训练】
31896053619501.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C
B.AD=CB
C.BE=DF 第1题图
D.AD∥BC
47136051314452.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( ) 第2题图
A.SAS B.ASA
C.AAS D.SSS
3.如图,已知在△ABC中,CD
是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
第3题图 第4题图
44754805791204.如图所示,已知∠1=∠2,AD=BC,AC,BD相交于点O,MN经过点O,则图中全等三角形的对数为( )
A.4对 B.5对 C.6对 D.7对
5.如图,∠B=∠DEF,AB=DE,要证明△ABC≌△DEF.
(1)若以“ASA”为依据,则还缺一个条件:____________. 第5题图
(2)若以“AAS”为依据,则还缺一个条件:____________________.
6.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中和△ABC全等的图形是________.
第6题图 第7题图
7.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,垂足为A,交CD于D,若AD=8,则点P到BC的距离是________.
32086555181608.(邵阳中考)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形.
(2)从(1)中任选一组进行证明.
第8题图
9.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.
第9题图
10.△ABC是格点三角形(顶点在网格线的交点),则图中能够作出与△ABC全等且有一条公共边的格点三角形(不含△ABC)的个数是________个.
第10题图 第11题图
11.如图,在△ABC中,AD平分∠BAC,AB=6,AC=4.若△ABD的面积等于9,则△ACD的面积为________.
12.如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.求证:
376110543815(1)△ABE≌△DCE.
(2)△ABC≌△DCB.
第12题图
13.如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,过点A作AE⊥l3于点E,求BE的长.
第13题图
386588026670014.如图,在四边形ABCD中,已知BD平分∠ABC,∠BAD+∠C=180°,求证:AD=CD.
第14题图
参考答案
1.5 三角形全等的判定(第4课时)
【笔记】
1.两角 对边 角角边 AAS
2.角两边
【训练】
1—4.BDCC
5.(1)∠A=∠D (2)∠ACB=∠F
6.乙、丙
7.4
8.(1)△ABE≌△CDF,△AFD≌△CEB(答案不唯一). (2)∵AB∥CD,∴∠1=∠2,∵AF=CE,∴AF+EF=CE+EF,即AE=FC,在△ABE和△CDF中,∴△ABE≌△CDF(AAS).
第8题图
9.∵BE⊥CE,AD⊥CE,∴∠CEB=∠ADC=90°,∵∠BCE+∠ACD=∠ACB=90°,∠CAD+∠ACD=180°-90°=90°,∴∠BCE=∠CAD,在△ACD和△CBE中,∴△CBE≌△ACD(AAS).
10.4
11.6
12.(1)在△ABE和△DCE中,∴△ABE≌△DCE(AAS). (2)∵△ABE≌△DCE,∴AE=DE,BE=CE,∴AC=DB.在△ABC和△DCB中,
∴△ABC≌△DCB(SAS).
13.过点C作CF⊥l3于点F.∵l1,l2之间的距离为1,l2,l3之间的距离为2,AE⊥l3,CF⊥l3,∴CF=3,∠AEB=∠BFC=90°.∴∠EAB+∠ABE=90°.∵∠ABC=90°,∴∠ABE+∠FBC=90°.∴∠EAB=∠FBC.在△AEB和△BFC中,∵∴△AEB≌△BFC(AAS).∴BE=CF=3.
第13题图 第14题图
14.过点D作DE⊥BA交BA的延长线于点E,过点D作DF⊥BC,垂足为F,∴∠AED=∠CFD=90°,∵BD平分∠ABC,∴DE=DF.∵∠BAD+∠C=180°,∠BAD+∠DAE=180°,∴∠DAE=∠C.在△AED和△CFD中,∴△AED≌△CFD(AAS),∴AD=CD.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
