1.5三角形全等的判定培优训练-2021-2022学年浙教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 1.5三角形全等的判定培优训练-2021-2022学年浙教版八年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 151.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 14:45:32 | ||
图片预览


文档简介
12115800114427001.5三角形全等的判定
1.如图,点E,F均在线段BC上,AB=DC,AE=DF,BF=CE.下列结论中,不一定成立的是( )
A. ∠B=∠C B. AF∥DE
C. AE=DE D. AB∥DC
,(第1题)) ,(第2题))
2.如图,AB=AD,BC=DC.若∠B=110°,∠BAD=90°,则∠BCA的度数为( )
A. 15° B. 20° C. 25° D. 30°
3.如图,△ABC的两边AB和AC的垂直平分线分别交BC于D,E两点.若BC的长为8 cm,则△ADE的周长为( )
A. 8 cm B. 16 cm
C. 4 cm D. 不能确定
4.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.有下列说法:①CE=BF;②AE=DF;③BF∥CE;④△BDF≌△CDE;⑤△ABD和△ACD面积相等.其中正确的说法有( )
A. 2个 B. 3个
C. 4个 D. 5个
5.根据下列已知条件,能画出唯一△ABC的是( )
A. ∠A=30°,∠B=60°,∠C=90°
B. AB=4,BC=3,∠A=30°
C. ∠A=60°,∠B=45°,AB=4
D. ∠C=90°,AB=6
6.如图,已知∠1=∠2,则下列条件中,不一定能使△ABD≌△ACD的条件是( )
A. AB=AC B. BD=CD
C. ∠B=∠C D. ∠BDA=∠CDA
,(第6题)) ,(第7题))
7.如图,已知AE⊥AB且AE=AB,BC⊥CD且BC=CD,按照图中所标注的数据,则图中阴影部分的面积S是( )
A. 50 B. 62
C. 65 D. 68
8.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=7,DE=2,则△BCE的面积等于( ) ,(第8题))
A. 14 B. 9
C. 7 D. 5
9.如图,已知AC=FC,CE是∠ACF的平分线,则图中全等三角形有( )
A. 1对 B. 2对
C. 3对 D. 4对
,(第9题))
10.如图,在△ABC中,已知AD=ED,AB=EB,∠A=80°,则∠CED=________.
(第10题)
11.(娄底中考)如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是______________________________ (只需写一个,不添加辅助线).
12.如图,AB,CD,EF交于点O,且它们都被点O平分,则图中共有____对全等三角形.
,(第12题))
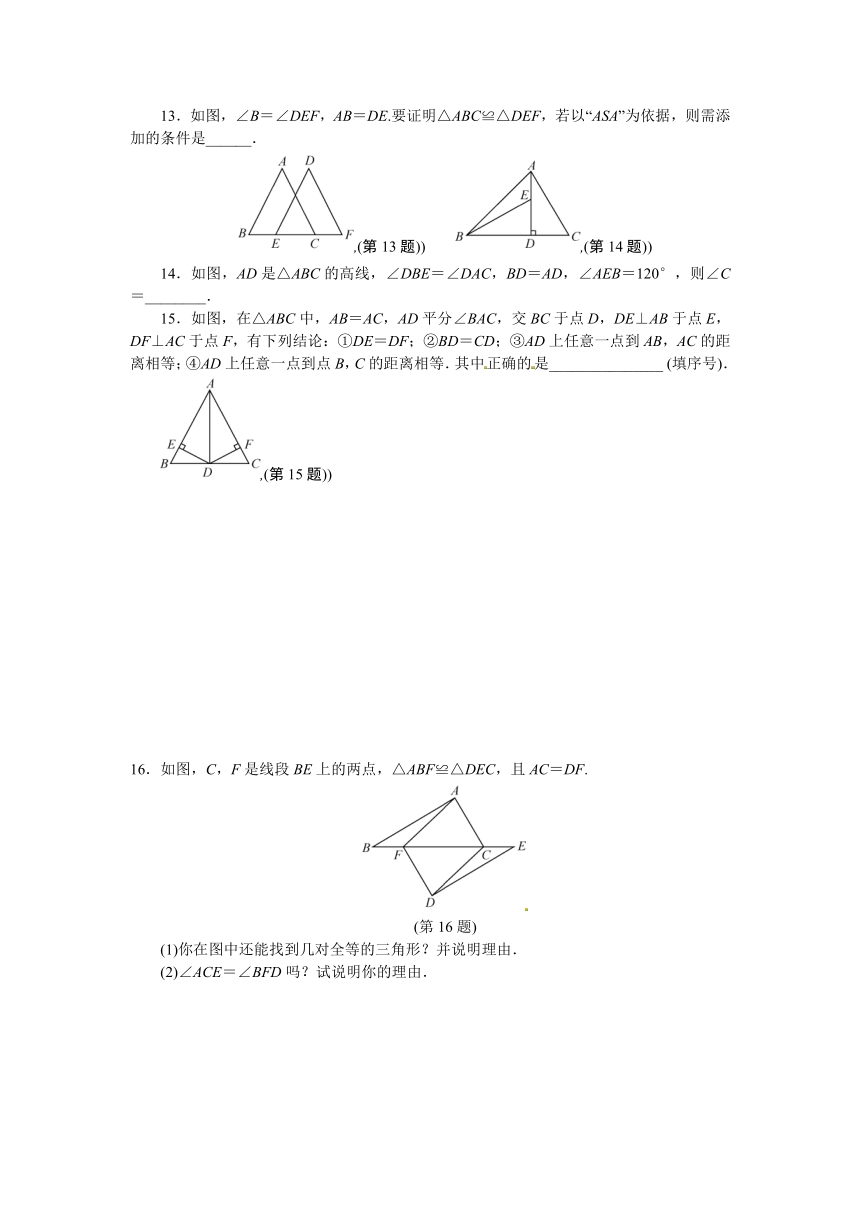
13.如图,∠B=∠DEF,AB=DE.要证明△ABC≌△DEF,若以“ASA”为依据,则需添加的条件是______.
,(第13题)) ,(第14题))
14.如图,AD是△ABC的高线,∠DBE=∠DAC,BD=AD,∠AEB=120°,则∠C=________.
15.如图,在△ABC中,AB=AC,AD平分∠BAC,交BC于点D,DE⊥AB于点E,DF⊥AC于点F,有下列结论:①DE=DF;②BD=CD;③AD上任意一点到AB,AC的距离相等;④AD上任意一点到点B,C的距离相等.其中正确的是_______________ (填序号).
,(第15题))
16.如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF.
(第16题)
(1)你在图中还能找到几对全等的三角形?并说明理由.
(2)∠ACE=∠BFD吗?试说明你的理由.
17.(杭州中考)如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN
(第17题)
18.如图,已知A是MD上一点,C是BQ上一点,AB∥CD,∠M=∠Q,P,N分别是MQ与CD,AB的交点,MN=PQ.求证:AM=CQ.
(第18题)
19.如图,△ABC的角平分线BE,CF交于点O,那么点O到△ABC三边的距离相等.为什么?
(第19题)
1-5C CAC C
6-9 BACD
10. 100°
11. ∠ABD=∠CBD或AD=CD
12. 3
13 ∠A=∠D
14. 60°
15. ①②③④
16【解】 (1)还能找到2对全等三角形,分别是△ACF≌△DFC,△ABC≌△DEF.理由如下:
∵△ABF≌△DEC,
∴AB=DE,BF=EC,AF=DC(全等三角形的对应边相等),
∴BF+FC=EC+FC,即BC=EF.
在△ACF和△DFC中,∵
∴△ACF≌△DFC(SSS).
在△ABC和△DEF中,∵
∴△ABC≌△DEF(SSS).
(2)∠ACE=∠BFD.理由如下:
∵△ABC≌△DEF,
∴∠ACB=∠DFE(全等三角形的对应角相等).
∵∠ACB+∠ACE=180°,∠DFE+∠BFD=180°,
∴∠ACE=∠BFD(等角的补角相等).
17【解】 ∵AM=2MB,AN=2NC,
∴AM=AB,AN=AC.
又∵AB=AC,∴AM=AN
∵AD平分∠BAC,
∴∠MAD=∠NAD.
又∵AD=AD,
∴△AMD≌△AND(SAS).∴DM=DN.
18.【解】 ∵AB∥CD,
∴∠MNA=∠MPD.
又∵∠QPC=∠MPD,∴∠MNA=∠QPC.
在△MNA和△QPC中,∵
∴△MNA≌△QPC(ASA).∴AM=CQ
19【解】 过点O作OG⊥BC,OH⊥AC,OI⊥AB,垂足分别为G,H,I
∵CF平分∠ACB,OG⊥BC,OH⊥AC,
∴OG=OH.
∵BE平分∠ABC,OG⊥BC,OI⊥AB,∴OG=OI,
∴OG=OH=OI,
即点O到△ABC三边的距离相等.
1.如图,点E,F均在线段BC上,AB=DC,AE=DF,BF=CE.下列结论中,不一定成立的是( )
A. ∠B=∠C B. AF∥DE
C. AE=DE D. AB∥DC
,(第1题)) ,(第2题))
2.如图,AB=AD,BC=DC.若∠B=110°,∠BAD=90°,则∠BCA的度数为( )
A. 15° B. 20° C. 25° D. 30°
3.如图,△ABC的两边AB和AC的垂直平分线分别交BC于D,E两点.若BC的长为8 cm,则△ADE的周长为( )
A. 8 cm B. 16 cm
C. 4 cm D. 不能确定
4.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.有下列说法:①CE=BF;②AE=DF;③BF∥CE;④△BDF≌△CDE;⑤△ABD和△ACD面积相等.其中正确的说法有( )
A. 2个 B. 3个
C. 4个 D. 5个
5.根据下列已知条件,能画出唯一△ABC的是( )
A. ∠A=30°,∠B=60°,∠C=90°
B. AB=4,BC=3,∠A=30°
C. ∠A=60°,∠B=45°,AB=4
D. ∠C=90°,AB=6
6.如图,已知∠1=∠2,则下列条件中,不一定能使△ABD≌△ACD的条件是( )
A. AB=AC B. BD=CD
C. ∠B=∠C D. ∠BDA=∠CDA
,(第6题)) ,(第7题))
7.如图,已知AE⊥AB且AE=AB,BC⊥CD且BC=CD,按照图中所标注的数据,则图中阴影部分的面积S是( )
A. 50 B. 62
C. 65 D. 68
8.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=7,DE=2,则△BCE的面积等于( ) ,(第8题))
A. 14 B. 9
C. 7 D. 5
9.如图,已知AC=FC,CE是∠ACF的平分线,则图中全等三角形有( )
A. 1对 B. 2对
C. 3对 D. 4对
,(第9题))
10.如图,在△ABC中,已知AD=ED,AB=EB,∠A=80°,则∠CED=________.
(第10题)
11.(娄底中考)如图,已知AB=BC,要使△ABD≌△CBD,还需添加一个条件,你添加的条件是______________________________ (只需写一个,不添加辅助线).
12.如图,AB,CD,EF交于点O,且它们都被点O平分,则图中共有____对全等三角形.
,(第12题))
13.如图,∠B=∠DEF,AB=DE.要证明△ABC≌△DEF,若以“ASA”为依据,则需添加的条件是______.
,(第13题)) ,(第14题))
14.如图,AD是△ABC的高线,∠DBE=∠DAC,BD=AD,∠AEB=120°,则∠C=________.
15.如图,在△ABC中,AB=AC,AD平分∠BAC,交BC于点D,DE⊥AB于点E,DF⊥AC于点F,有下列结论:①DE=DF;②BD=CD;③AD上任意一点到AB,AC的距离相等;④AD上任意一点到点B,C的距离相等.其中正确的是_______________ (填序号).
,(第15题))
16.如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF.
(第16题)
(1)你在图中还能找到几对全等的三角形?并说明理由.
(2)∠ACE=∠BFD吗?试说明你的理由.
17.(杭州中考)如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN
(第17题)
18.如图,已知A是MD上一点,C是BQ上一点,AB∥CD,∠M=∠Q,P,N分别是MQ与CD,AB的交点,MN=PQ.求证:AM=CQ.
(第18题)
19.如图,△ABC的角平分线BE,CF交于点O,那么点O到△ABC三边的距离相等.为什么?
(第19题)
1-5C CAC C
6-9 BACD
10. 100°
11. ∠ABD=∠CBD或AD=CD
12. 3
13 ∠A=∠D
14. 60°
15. ①②③④
16【解】 (1)还能找到2对全等三角形,分别是△ACF≌△DFC,△ABC≌△DEF.理由如下:
∵△ABF≌△DEC,
∴AB=DE,BF=EC,AF=DC(全等三角形的对应边相等),
∴BF+FC=EC+FC,即BC=EF.
在△ACF和△DFC中,∵
∴△ACF≌△DFC(SSS).
在△ABC和△DEF中,∵
∴△ABC≌△DEF(SSS).
(2)∠ACE=∠BFD.理由如下:
∵△ABC≌△DEF,
∴∠ACB=∠DFE(全等三角形的对应角相等).
∵∠ACB+∠ACE=180°,∠DFE+∠BFD=180°,
∴∠ACE=∠BFD(等角的补角相等).
17【解】 ∵AM=2MB,AN=2NC,
∴AM=AB,AN=AC.
又∵AB=AC,∴AM=AN
∵AD平分∠BAC,
∴∠MAD=∠NAD.
又∵AD=AD,
∴△AMD≌△AND(SAS).∴DM=DN.
18.【解】 ∵AB∥CD,
∴∠MNA=∠MPD.
又∵∠QPC=∠MPD,∴∠MNA=∠QPC.
在△MNA和△QPC中,∵
∴△MNA≌△QPC(ASA).∴AM=CQ
19【解】 过点O作OG⊥BC,OH⊥AC,OI⊥AB,垂足分别为G,H,I
∵CF平分∠ACB,OG⊥BC,OH⊥AC,
∴OG=OH.
∵BE平分∠ABC,OG⊥BC,OI⊥AB,∴OG=OI,
∴OG=OH=OI,
即点O到△ABC三边的距离相等.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
