《3.1 圆》课时同步训练2020-2021学年九年级数学浙教版上册(Word版 含答案)
文档属性
| 名称 | 《3.1 圆》课时同步训练2020-2021学年九年级数学浙教版上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 221.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览




文档简介
《3.1 圆》课时同步训练2020-2021年数学浙教新版九(上)
一.选择题(共9小题)
1.已知⊙O与点P在同一平面内,如果⊙O的直径为6,线段OP的长为4,则下列说法正确的是( )
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法判断点P与⊙O的位置关系
2.在平面直角坐标系xOy中,⊙O的半径为2,点A(1,)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
3.三角形的外心是三角形的( )
A.三条中线的交点 B.三条中垂线的交点
C.三条高的交点 D.三条角平分线的交点
4.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
5.下列说法错误的是( )
A.已知圆心和半径可以作一个圆
B.经过一个已知点A的圆能作无数个
C.经过两个已知点A,B的圆能作两个
D.经过不在同一直线上的三个点A,B,C只能作一个圆
6.如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4),(5,4),(1,0),则以A、B、C为顶点的三角形外接圆的圆心坐标是( )
A.(3,2) B.(2,3) C.(1,3) D.(3,1)
7.数轴上有两个点A和B,点B表示实数6,点A表示实数a,⊙B半径为4.若点A在⊙B内,则( )
A.a<2或a>10 B.2<a<10 C.a>2 D.a<10
8.已知△ABC中,∠C=90°,AC=3,BC=4,点P为边AB的中点,以点C为圆心,长度r为半径画圆,使得点A,P在⊙O内,点B在⊙C外,则半径r的取值范围是( )
A. B. C.3<r<4 D.r>3
9.在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是( )
A.当a=﹣1时,点B在圆A上
B.当a<1时,点B在圆A内
C.当a<﹣1时,点B在圆A外
D.当﹣1<a<3时,点B在圆A内
二.填空题(共6小题)
10.在Rt△ABC中,∠C=90°,AC=4,BC=3,则其外接圆的直径为 .
11.已知⊙O的半径为1,点P与点O之间的距离为d,且关于x的方程x2﹣2x+d=0没有实数根,则点P在 (填“圆内”“圆上”或“圆外”).
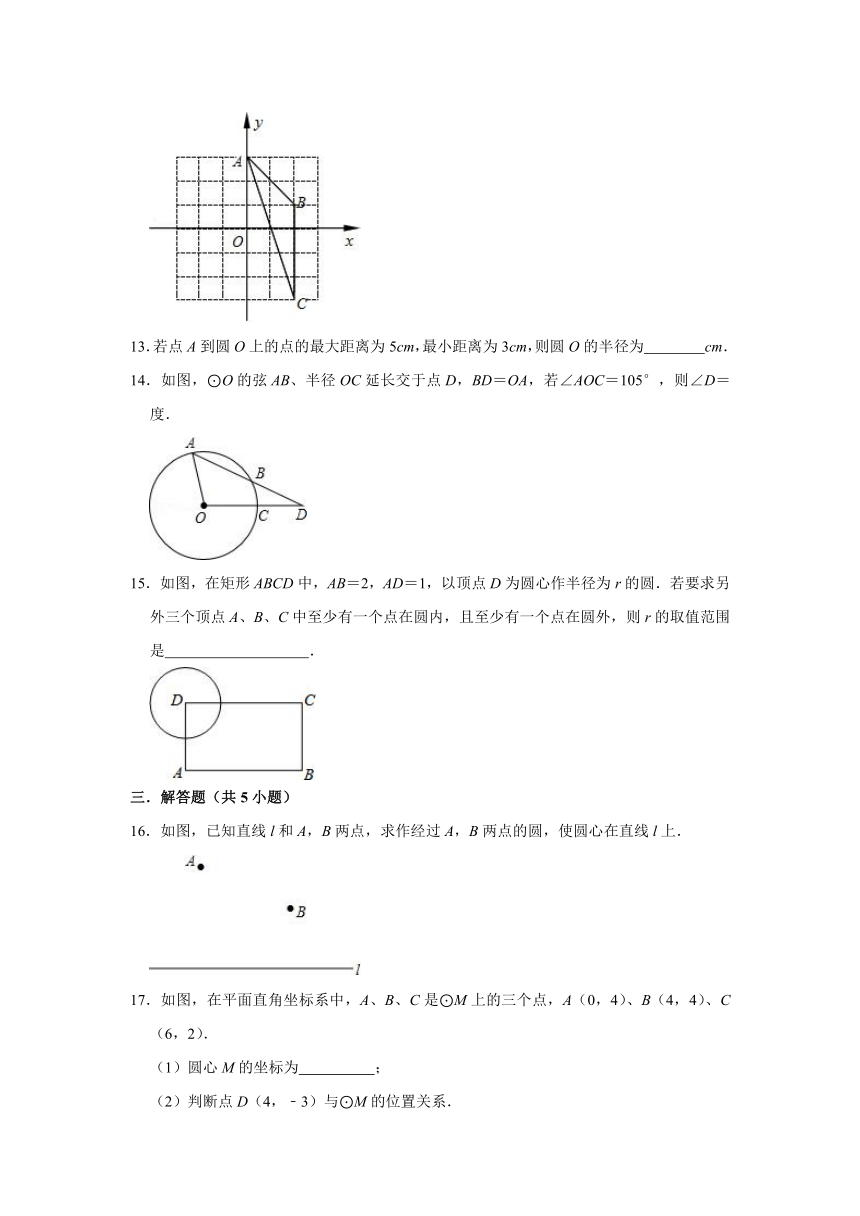
12.如图,在平面直角坐标系xOy中,点A(0,3),点B(2,1),点C(2,﹣3).则经画图操作可知:△ABC的外心坐标应是 .
13.若点A到圆O上的点的最大距离为5cm,最小距离为3cm,则圆O的半径为 cm.
14.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
15.如图,在矩形ABCD中,AB=2,AD=1,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
三.解答题(共5小题)
16.如图,已知直线l和A,B两点,求作经过A,B两点的圆,使圆心在直线l上.
17.如图,在平面直角坐标系中,A、B、C是⊙M上的三个点,A(0,4)、B(4,4)、C(6,2).
(1)圆心M的坐标为 ;
(2)判断点D(4,﹣3)与⊙M的位置关系.
18.已知:如图,圆O是△ABC的外接圆,AO平分∠BAC.
(1)求证:△ABC是等腰三角形;
(2)当OA=4,AB=6,求边BC的长.
19.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
20.如图,城市A的正北方向50千米的B处,有一无线电信号发射塔.已知,该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的班车速度为60千米/小时.
(1)当班车从A城出发开往C城时,某人立即打开无线电收音机,班车行驶了0.5小时的时候,接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2小时,请你判断到C城后还能接收到信号吗?请说明理由.
参考答案
一.选择题(共9小题)
1.解:∵⊙O的半径是3,线段OP的长为4,
即点P到圆心的距离大于圆的半径,
∴点P在⊙O外.
故选:C.
2.解:∵点A(1,),
∴AO==2,
∵⊙O的半径为2,
∴点A在⊙O上,
故选:A.
3.解:根据三角形外心的定义可知:三角形的外心是三条中垂线的交点.
故选:B.
4.解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
5.解:A、已知圆心和半径可以作一个圆,说法正确,故不符合题意.
B、只有确定圆心和半径才能确定一个圆,所以经过一个已知点A的圆能作无数个,说法正确,故不符合题意.
C、只有确定圆心和半径才能确定一个圆,所以已知点A,B的圆能作无数个,说法错误,故符合题意.
D、经过不在同一直线上的三个点A,B,C只能作一个圆,说法正确,故不符合题意.
故选:C.
6.解:根据垂径定理的推论,如图,
作弦AB、AC的垂直平分线,
交点O′即为三角形外接圆的圆心,
且O′坐标是(3,2).
故选:A.
7.解:∵点B表示实数6,⊙B半径为4.
∴数轴与⊙B的交点表示的数为2或10,
∵点A表示实数a,点A在⊙B内,
∴2<a<10,
故选:B.
8.解:由AC=3,BC=4,以点C为圆心,长度r为半径画圆,使得点A,P在⊙O内,点B在⊙C外,得
3<r<4,
故选:C.
9.解:如图:
∵A(1,0),⊙A的半径是2,
∴AC=AE=2,
∴OE=1,OC=3,
A、当a=﹣1时,点B在E上,即B在⊙A上,正确,故本选项不合题意;
B、当a=﹣3时,B在⊙A外,即说当a<1时,点B在圆A内错误,故本选项符合题意;
C、当a<﹣1时,AB>2,即说点B在圆A外正确,故本选项不合题意;
D、当﹣1<a<3时,B在⊙A内正确,故本选项不合题意;
故选:B.
二.填空题(共6小题)
10.解:在Rt△ABC中,
∵∠ACB=90°,AC=4,BC=3,
∴AB===5,
∵直角三角形的外心为斜边中点,
∴Rt△ABC的外接圆的直径为5.
故答案为:5.
11.解:∵方程x2﹣2x+d=0没有实数根,
∴△=b2﹣4ac=4﹣4d<0,
∴d>1,
∵⊙O的半径为1,
∴d>r;
∴点P在⊙O的外部,
故答案为:圆外.
12.解:∵△ABC的外心即是三角形三边垂直平分线的交点,
∴作图得:
∴EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1)
13.解:点A应分为位于圆的内部于外部两种情况讨论.
当点A在圆内时,直径是5+3=8(cm),因而半径是4cm;
当点A在圆外时,直径是5﹣3=2(cm),因而半径是1cm.
故答案为:4或1.
14.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
15.解:在直角△ABD中,CD=AB=2,AD=1,
则BD==.
由图可知1<r<.
故答案为:1<r<.
三.解答题(共5小题)
16.解:如图所示,⊙O即为所求.
17.解:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,0)
故答案为:2,0.
(2)圆的半径AM==2,
线段MD==<2,
所以点D在⊙M内.
18.解:(1)连接OB、OC,
∵OA=OB=OC,OA平分∠BAC,
∴∠OBA=∠OCA=∠BAO=∠CAO,
在△OAB和△OAC中,
,
∴△OAB≌△OAC(AAS),
∴AB=AC
即△ABC是等腰三角形;
(2)延长AO交BC于点H,
∵AH平分∠BAC,AB=AC,
∴AH⊥BC,BH=CH,
设OH=b,BH=CH=a,
∵BH2+OH2=OB2,BH2+AH2=AB2,OA=4,AB=6,
∴,
解得,,
∴BC=2a=3.
19.解:(1)∵矩形ABCD中AB=3,AD=4,
∴AC=BD==5,
∵AF?BD=AB?AD,
∴AF==,
同理可得DE=,
在Rt△ADE中,AE==;
(2)∵AF<AB<AE<AD<AC,
∴若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,即点F在圆内,点D、C在圆外,
∴⊙A的半径r的取值范围为2.4<r<4.
20.解:(1)过点B作BM⊥AC于点M,
设班车行驶了0.5小时的时候到达M点.根据此时接受信号最强,则BM⊥AC,又AM=30千米,AB=50千米.
所以BM=40千米.
答:车到发射塔的距离是40千米.
(2)连接BC,
∵AC=60×2=120(千米),AM=30千米,
∴CM=AC﹣AM=90(千米),
∴BC==10<100.
答:到C城能接到信号.
一.选择题(共9小题)
1.已知⊙O与点P在同一平面内,如果⊙O的直径为6,线段OP的长为4,则下列说法正确的是( )
A.点P在⊙O上
B.点P在⊙O内
C.点P在⊙O外
D.无法判断点P与⊙O的位置关系
2.在平面直角坐标系xOy中,⊙O的半径为2,点A(1,)与⊙O的位置关系是( )
A.在⊙O上 B.在⊙O内 C.在⊙O外 D.不能确定
3.三角形的外心是三角形的( )
A.三条中线的交点 B.三条中垂线的交点
C.三条高的交点 D.三条角平分线的交点
4.小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是( )
A.① B.② C.③ D.④
5.下列说法错误的是( )
A.已知圆心和半径可以作一个圆
B.经过一个已知点A的圆能作无数个
C.经过两个已知点A,B的圆能作两个
D.经过不在同一直线上的三个点A,B,C只能作一个圆
6.如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4),(5,4),(1,0),则以A、B、C为顶点的三角形外接圆的圆心坐标是( )
A.(3,2) B.(2,3) C.(1,3) D.(3,1)
7.数轴上有两个点A和B,点B表示实数6,点A表示实数a,⊙B半径为4.若点A在⊙B内,则( )
A.a<2或a>10 B.2<a<10 C.a>2 D.a<10
8.已知△ABC中,∠C=90°,AC=3,BC=4,点P为边AB的中点,以点C为圆心,长度r为半径画圆,使得点A,P在⊙O内,点B在⊙C外,则半径r的取值范围是( )
A. B. C.3<r<4 D.r>3
9.在直角坐标平面内,点A的坐标为(1,0),点B的坐标为(a,0),圆A的半径为2.下列说法中不正确的是( )
A.当a=﹣1时,点B在圆A上
B.当a<1时,点B在圆A内
C.当a<﹣1时,点B在圆A外
D.当﹣1<a<3时,点B在圆A内
二.填空题(共6小题)
10.在Rt△ABC中,∠C=90°,AC=4,BC=3,则其外接圆的直径为 .
11.已知⊙O的半径为1,点P与点O之间的距离为d,且关于x的方程x2﹣2x+d=0没有实数根,则点P在 (填“圆内”“圆上”或“圆外”).
12.如图,在平面直角坐标系xOy中,点A(0,3),点B(2,1),点C(2,﹣3).则经画图操作可知:△ABC的外心坐标应是 .
13.若点A到圆O上的点的最大距离为5cm,最小距离为3cm,则圆O的半径为 cm.
14.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D= 度.
15.如图,在矩形ABCD中,AB=2,AD=1,以顶点D为圆心作半径为r的圆.若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
三.解答题(共5小题)
16.如图,已知直线l和A,B两点,求作经过A,B两点的圆,使圆心在直线l上.
17.如图,在平面直角坐标系中,A、B、C是⊙M上的三个点,A(0,4)、B(4,4)、C(6,2).
(1)圆心M的坐标为 ;
(2)判断点D(4,﹣3)与⊙M的位置关系.
18.已知:如图,圆O是△ABC的外接圆,AO平分∠BAC.
(1)求证:△ABC是等腰三角形;
(2)当OA=4,AB=6,求边BC的长.
19.如图,矩形ABCD中AB=3,AD=4.作DE⊥AC于点E,作AF⊥BD于点F.
(1)求AF、AE的长;
(2)若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,求⊙A的半径r的取值范围.
20.如图,城市A的正北方向50千米的B处,有一无线电信号发射塔.已知,该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的班车速度为60千米/小时.
(1)当班车从A城出发开往C城时,某人立即打开无线电收音机,班车行驶了0.5小时的时候,接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2小时,请你判断到C城后还能接收到信号吗?请说明理由.
参考答案
一.选择题(共9小题)
1.解:∵⊙O的半径是3,线段OP的长为4,
即点P到圆心的距离大于圆的半径,
∴点P在⊙O外.
故选:C.
2.解:∵点A(1,),
∴AO==2,
∵⊙O的半径为2,
∴点A在⊙O上,
故选:A.
3.解:根据三角形外心的定义可知:三角形的外心是三条中垂线的交点.
故选:B.
4.解:第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.
故选:A.
5.解:A、已知圆心和半径可以作一个圆,说法正确,故不符合题意.
B、只有确定圆心和半径才能确定一个圆,所以经过一个已知点A的圆能作无数个,说法正确,故不符合题意.
C、只有确定圆心和半径才能确定一个圆,所以已知点A,B的圆能作无数个,说法错误,故符合题意.
D、经过不在同一直线上的三个点A,B,C只能作一个圆,说法正确,故不符合题意.
故选:C.
6.解:根据垂径定理的推论,如图,
作弦AB、AC的垂直平分线,
交点O′即为三角形外接圆的圆心,
且O′坐标是(3,2).
故选:A.
7.解:∵点B表示实数6,⊙B半径为4.
∴数轴与⊙B的交点表示的数为2或10,
∵点A表示实数a,点A在⊙B内,
∴2<a<10,
故选:B.
8.解:由AC=3,BC=4,以点C为圆心,长度r为半径画圆,使得点A,P在⊙O内,点B在⊙C外,得
3<r<4,
故选:C.
9.解:如图:
∵A(1,0),⊙A的半径是2,
∴AC=AE=2,
∴OE=1,OC=3,
A、当a=﹣1时,点B在E上,即B在⊙A上,正确,故本选项不合题意;
B、当a=﹣3时,B在⊙A外,即说当a<1时,点B在圆A内错误,故本选项符合题意;
C、当a<﹣1时,AB>2,即说点B在圆A外正确,故本选项不合题意;
D、当﹣1<a<3时,B在⊙A内正确,故本选项不合题意;
故选:B.
二.填空题(共6小题)
10.解:在Rt△ABC中,
∵∠ACB=90°,AC=4,BC=3,
∴AB===5,
∵直角三角形的外心为斜边中点,
∴Rt△ABC的外接圆的直径为5.
故答案为:5.
11.解:∵方程x2﹣2x+d=0没有实数根,
∴△=b2﹣4ac=4﹣4d<0,
∴d>1,
∵⊙O的半径为1,
∴d>r;
∴点P在⊙O的外部,
故答案为:圆外.
12.解:∵△ABC的外心即是三角形三边垂直平分线的交点,
∴作图得:
∴EF与MN的交点O′即为所求的△ABC的外心,
∴△ABC的外心坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1)
13.解:点A应分为位于圆的内部于外部两种情况讨论.
当点A在圆内时,直径是5+3=8(cm),因而半径是4cm;
当点A在圆外时,直径是5﹣3=2(cm),因而半径是1cm.
故答案为:4或1.
14.解:连接OB,
∵BD=OA,OA=OB
所以△AOB和△BOD为等腰三角形,
设∠D=x度,则∠OBA=2x°,
因为OB=OA,
所以∠A=2x°,
在△AOB中,2x+2x+(105﹣x)=180,
解得x=25,
即∠D=25°.
15.解:在直角△ABD中,CD=AB=2,AD=1,
则BD==.
由图可知1<r<.
故答案为:1<r<.
三.解答题(共5小题)
16.解:如图所示,⊙O即为所求.
17.解:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,0)
故答案为:2,0.
(2)圆的半径AM==2,
线段MD==<2,
所以点D在⊙M内.
18.解:(1)连接OB、OC,
∵OA=OB=OC,OA平分∠BAC,
∴∠OBA=∠OCA=∠BAO=∠CAO,
在△OAB和△OAC中,
,
∴△OAB≌△OAC(AAS),
∴AB=AC
即△ABC是等腰三角形;
(2)延长AO交BC于点H,
∵AH平分∠BAC,AB=AC,
∴AH⊥BC,BH=CH,
设OH=b,BH=CH=a,
∵BH2+OH2=OB2,BH2+AH2=AB2,OA=4,AB=6,
∴,
解得,,
∴BC=2a=3.
19.解:(1)∵矩形ABCD中AB=3,AD=4,
∴AC=BD==5,
∵AF?BD=AB?AD,
∴AF==,
同理可得DE=,
在Rt△ADE中,AE==;
(2)∵AF<AB<AE<AD<AC,
∴若以点A为圆心作圆,B、C、D、E、F五点中至少有1个点在圆内,且至少有2个点在圆外,即点F在圆内,点D、C在圆外,
∴⊙A的半径r的取值范围为2.4<r<4.
20.解:(1)过点B作BM⊥AC于点M,
设班车行驶了0.5小时的时候到达M点.根据此时接受信号最强,则BM⊥AC,又AM=30千米,AB=50千米.
所以BM=40千米.
答:车到发射塔的距离是40千米.
(2)连接BC,
∵AC=60×2=120(千米),AM=30千米,
∴CM=AC﹣AM=90(千米),
∴BC==10<100.
答:到C城能接到信号.
同课章节目录
