3.4《圆心角》课时练习2021-2022学年浙教版数学九年级上册 (Word版 含答案)
文档属性
| 名称 | 3.4《圆心角》课时练习2021-2022学年浙教版数学九年级上册 (Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 156.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 15:13:02 | ||
图片预览

文档简介
浙教版数学九年级上册
3.4《圆心角》课时练习
一、选择题
1.下列语句中正确的是( )
A.长度相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
2.如图,AB、CD是⊙O的两条弦,连结AD、BC.若∠BCD=70°,则∠BAD的度数为( )
A.40° B.50° C.60° D.70°
3.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50°?? B.60°?? C.70°?? D.80°
5.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于(? )
A.25°????? B.30°????? C.35°???? D.50°?
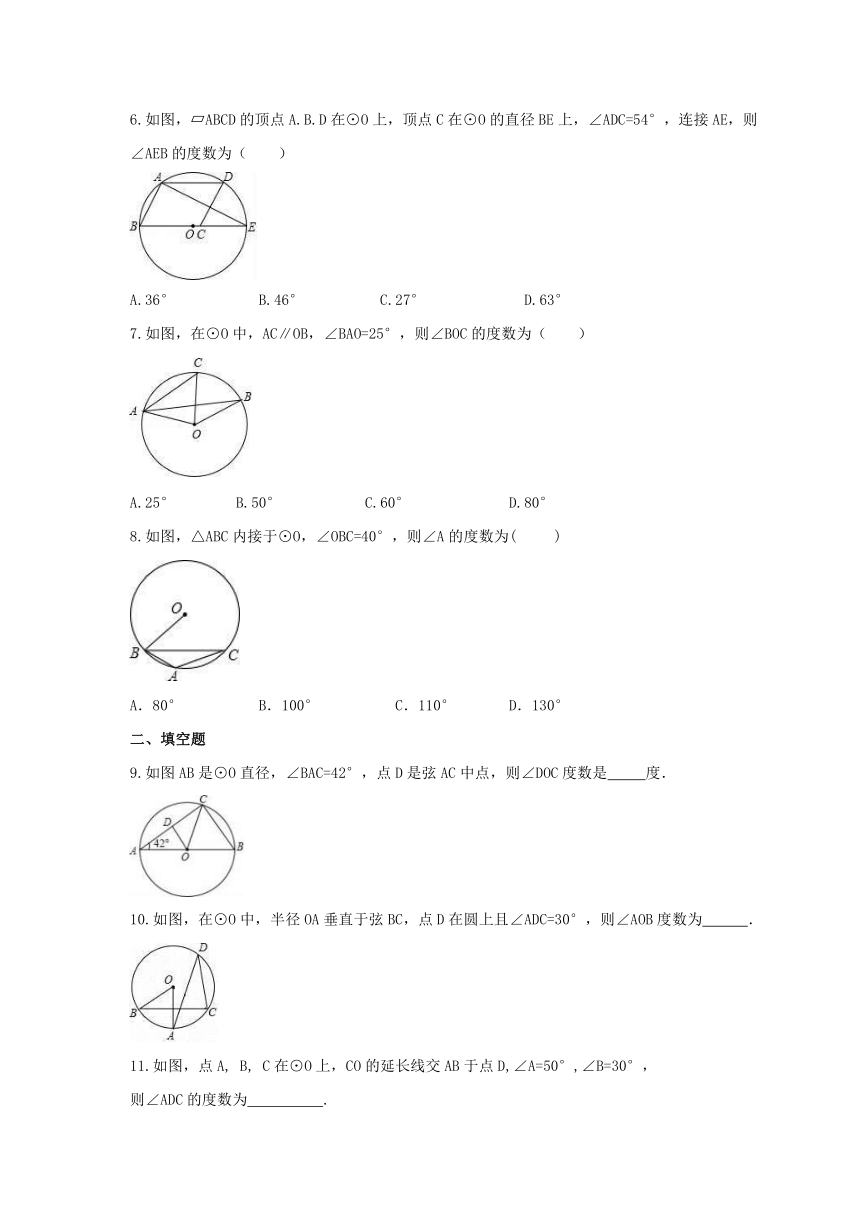
6.如图,?ABCD的顶点A.B.D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A.36°?? ? B.46°? ?? C.27°? ? D.63°
7.如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A.25° B.50° C.60° D.80°
8.如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )
A.80° B.100° C.110° D.130°
二、填空题
9.如图AB是⊙O直径,∠BAC=42°,点D是弦AC中点,则∠DOC度数是 度.
10.如图,在⊙O中,半径OA垂直于弦BC,点D在圆上且∠ADC=30°,则∠AOB度数为 ? .
11.如图,点A, B, C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,
则∠ADC的度数为 .
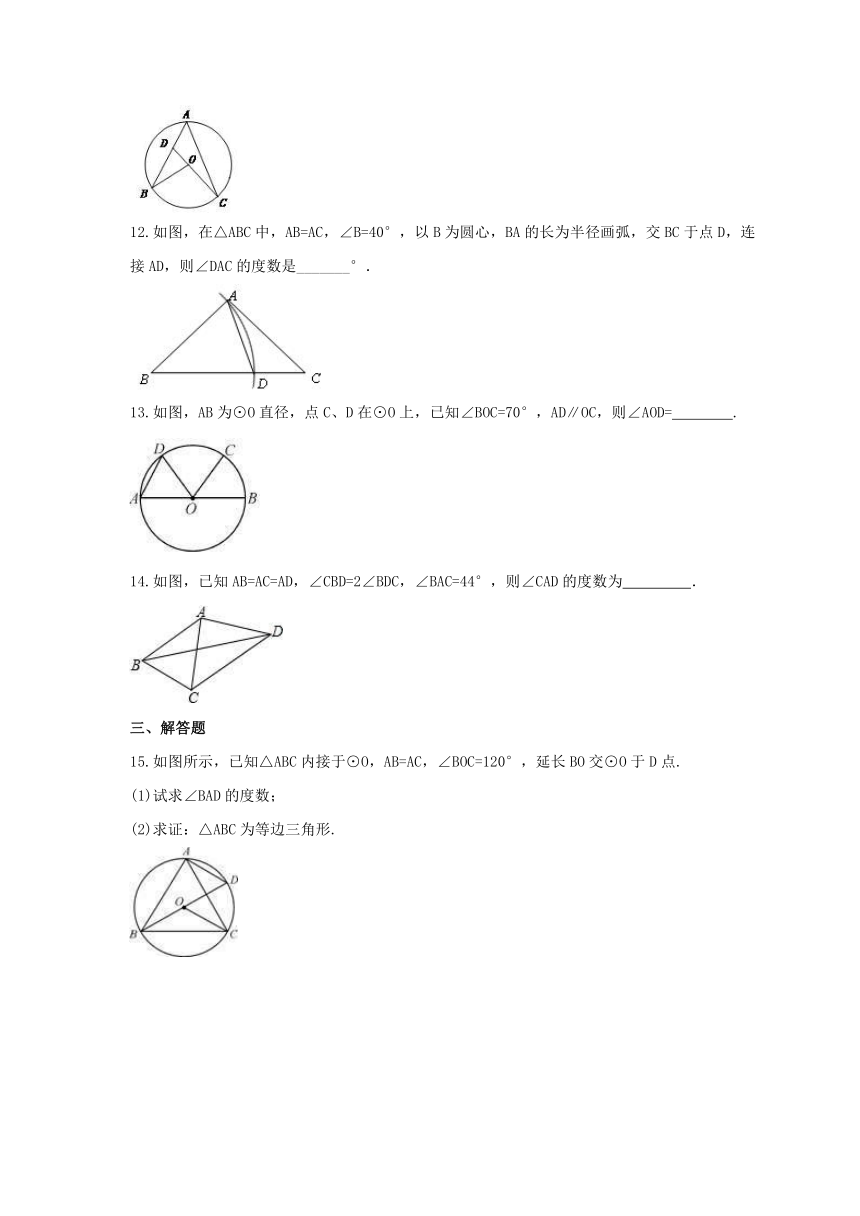
12.如图,在△ABC中,AB=AC,∠B=40°,以B为圆心,BA的长为半径画弧,交BC于点D,连接AD,则∠DAC的度数是_______°.
13.如图,AB为⊙O直径,点C、D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD=?? .
14.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为 .
三、解答题
15.如图所示,已知△ABC内接于⊙O,AB=AC,∠BOC=120°,延长BO交⊙O于D点.
(1)试求∠BAD的度数;
(2)求证:△ABC为等边三角形.
16.已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,
过点P作PD⊥OP交圆O于点D.
(1)如图1,当PD//AB时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
17.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
18.如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°
(1) 若点C在优弧BD上,求∠ACD的大小
(2) 若点C在劣弧BD上,直接写出∠ACD的大小
参考答案
1.D
2.D
3.D
4.C?
5.A
6.A.
7.B.
8.D
9.答案为:48.
10.答案为:60°.
11.答案为:110°
12.答案为:30;
13.答案为:40°?
14.答案为:88°.
15.解:(1)∵BD是⊙O的直径,
∴∠BAD=90°(直径所对的圆周角是直角).
(2)证明:∵∠BOC=120°,
∴∠BAC=∠BOC=60°.
又∵AB=AC,
∴△ABC是等边三角形.
16.(1)解:联结
∵直径
∴
∵
∴?
∵
∴?
∴
又∵,
∴
∵在中,
∴
∴
(2)过点作,垂足为
∵
∴
∵,
∴,
∵在⊙中,
∴
∵平分
∴
∴
17.解:(1)∵BC=DC,
∴∠CBD=∠CDB=39°,
∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°;
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠CBD,
∴∠1=∠2.
18.解:
3.4《圆心角》课时练习
一、选择题
1.下列语句中正确的是( )
A.长度相等的两条弧是等弧
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.经过圆心的每一条直线都是圆的对称轴
2.如图,AB、CD是⊙O的两条弦,连结AD、BC.若∠BCD=70°,则∠BAD的度数为( )
A.40° B.50° C.60° D.70°
3.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50°?? B.60°?? C.70°?? D.80°
5.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于(? )
A.25°????? B.30°????? C.35°???? D.50°?
6.如图,?ABCD的顶点A.B.D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为( )
A.36°?? ? B.46°? ?? C.27°? ? D.63°
7.如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A.25° B.50° C.60° D.80°
8.如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )
A.80° B.100° C.110° D.130°
二、填空题
9.如图AB是⊙O直径,∠BAC=42°,点D是弦AC中点,则∠DOC度数是 度.
10.如图,在⊙O中,半径OA垂直于弦BC,点D在圆上且∠ADC=30°,则∠AOB度数为 ? .
11.如图,点A, B, C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,
则∠ADC的度数为 .
12.如图,在△ABC中,AB=AC,∠B=40°,以B为圆心,BA的长为半径画弧,交BC于点D,连接AD,则∠DAC的度数是_______°.
13.如图,AB为⊙O直径,点C、D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD=?? .
14.如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为 .
三、解答题
15.如图所示,已知△ABC内接于⊙O,AB=AC,∠BOC=120°,延长BO交⊙O于D点.
(1)试求∠BAD的度数;
(2)求证:△ABC为等边三角形.
16.已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,
过点P作PD⊥OP交圆O于点D.
(1)如图1,当PD//AB时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
17.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
18.如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°
(1) 若点C在优弧BD上,求∠ACD的大小
(2) 若点C在劣弧BD上,直接写出∠ACD的大小
参考答案
1.D
2.D
3.D
4.C?
5.A
6.A.
7.B.
8.D
9.答案为:48.
10.答案为:60°.
11.答案为:110°
12.答案为:30;
13.答案为:40°?
14.答案为:88°.
15.解:(1)∵BD是⊙O的直径,
∴∠BAD=90°(直径所对的圆周角是直角).
(2)证明:∵∠BOC=120°,
∴∠BAC=∠BOC=60°.
又∵AB=AC,
∴△ABC是等边三角形.
16.(1)解:联结
∵直径
∴
∵
∴?
∵
∴?
∴
又∵,
∴
∵在中,
∴
∴
(2)过点作,垂足为
∵
∴
∵,
∴,
∵在⊙中,
∴
∵平分
∴
∴
17.解:(1)∵BC=DC,
∴∠CBD=∠CDB=39°,
∵∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°;
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠CBD,
∴∠1=∠2.
18.解:
同课章节目录
