《1.1 认识三角形》课时同步练习 2021-2022学年浙教版数学八年级上册(word版含解析)
文档属性
| 名称 | 《1.1 认识三角形》课时同步练习 2021-2022学年浙教版数学八年级上册(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 119.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 15:16:18 | ||
图片预览



文档简介
1144270012611100《1.1 认识三角形》课时同步练习2020-2021年数学浙教新版八(上)
一.选择题(共9小题)
1.如图,将一副直角三角板按如图所示叠放,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的大小是( )
A.10° B.15° C.25° D.30°
2.下列四组长度的小木棒中,按首尾顺次连接能组成一个三角形的是( )
A.1,2,3 B.4,5,6 C.3,4,12 D.4,8,4
3.若△ABC的三个内角的比为3:5:2,则△ABC是( )
A.等腰三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
4.下列长度的各组线段能组成一个三角形的是( )
A.1cm,2cm,3cm B.2cm,2cm,4cm
C.3cm,4cm,7cm D.3cm,3cm,4cm
5.如图,为估计池塘岸边两点A、B的距离,小方在池塘的一侧选取一点O,测得OA=6cm,OB=4cm,则点A、B间的距离不可能是( )
A.10 cm B.8cm C.6cm D.4cm
6.如图,△ABC的面积为12cm2,点D在BC边上,E是AD的中点,则△BCE的面积是( )
A.4cm2 B.6cm2 C.8cm2 D.10cm2
7.已知:a,b,c是△ABC的三边,且a:b:c=4:5:6,则它们的对应高ha:hb:hc的比是( )
A.4:5:6 B.6:5:4 C.15:12:10 D.10:12:15
8.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
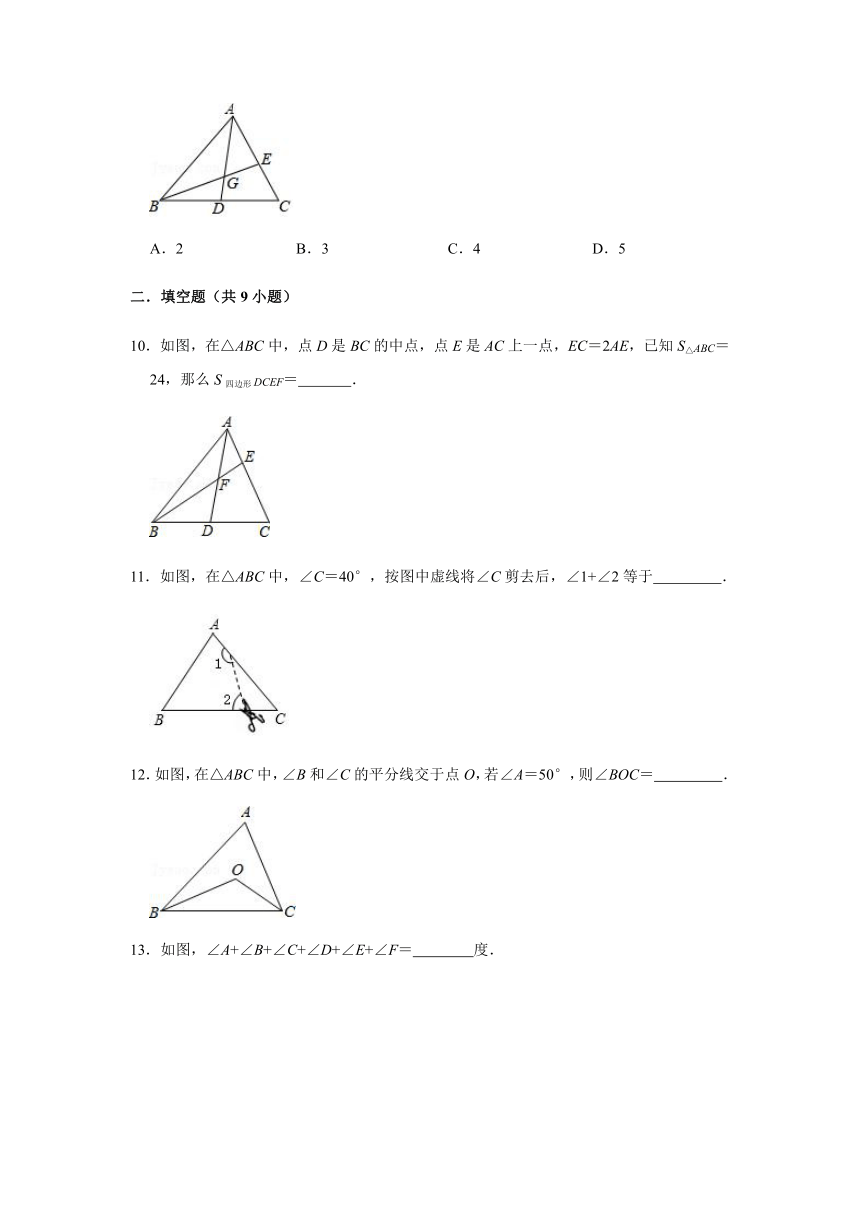
9.如图,在△ABC中,D,E分别是BC,AC的中点,AD和BE相交于点G,若AD=6,则AG的长度为( )
A.2 B.3 C.4 D.5
二.填空题(共9小题)
10.如图,在△ABC中,点D是BC的中点,点E是AC上一点,EC=2AE,已知S△ABC=24,那么S四边形DCEF= .
11.如图,在△ABC中,∠C=40°,按图中虚线将∠C剪去后,∠1+∠2等于 .
12.如图,在△ABC中,∠B和∠C的平分线交于点O,若∠A=50°,则∠BOC= .
13.如图,∠A+∠B+∠C+∠D+∠E+∠F= 度.
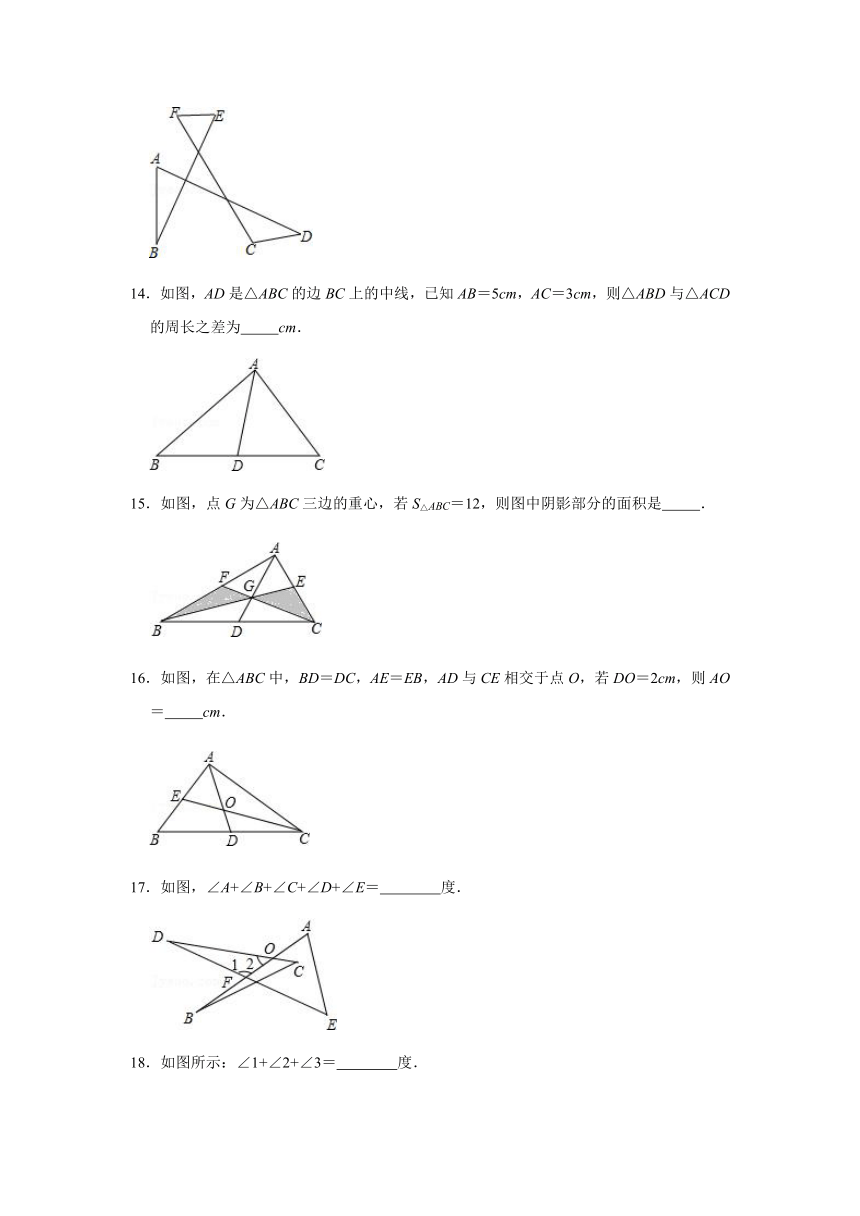
14.如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,则△ABD与△ACD的周长之差为 cm.
15.如图,点G为△ABC三边的重心,若S△ABC=12,则图中阴影部分的面积是 .
16.如图,在△ABC中,BD=DC,AE=EB,AD与CE相交于点O,若DO=2cm,则AO= cm.
17.如图,∠A+∠B+∠C+∠D+∠E= 度.
18.如图所示:∠1+∠2+∠3= 度.
三.解答题(共4小题)
19.如图,在△ABC中,∠B=40°,∠C=60°,点D是BC边上的一点,将△ACD沿AD折叠,点C恰好落在BC边上的点E处.
(1)直接填空:∠ADE的大小是 ;
(2)求∠BAE的大小.
20.如图,点D是三角形ABC的边BC延长线上一点,CE∥AB,求证:∠A+∠B+∠ACB=180°.
21.一个三角形的周长为36cm,三边之比a:b:c=2:3:4,求a,b,c的值.
22.如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
参考答案
一.选择题(共9小题)
1.解:∵∠B=45°,
∴∠BAC=45°,
∴∠EAF=135°,
∴∠AFD=135°+30°=165°,
∴∠BFD=180°﹣∠AFD=15°
故选:B.
2.解:A、1+2=3,不满足三角形三边关系定理,故错误,不符合题意;
B、4+5>6,满足三边关系定理,故正确,符合题意;
C、3+4<12.不满足三边关系定理,故错误,不符合题意;
D、4+4=8.不满足三角形三边关系定理,故错误,不符合题意.
故选:B.
3.解:∵△ABC的三个内角的比为3:5:2可设此三角形的三个内角分别为2x,3x,5x,
∴2x+3x+5x=180°,解得x=18°,
∴5x=5×18°=90°.
∴此三角形是直角三角形.
故选:C.
4.解:A、∵1+2=3,∴不能组成三角形,故本选项错误;
B、∵2+2=4,∴不能组成三角形,故本选项错误;
C、∵3+4=7,∴不能组成三角形,故本选项错误;
D、∵4+5=9>6,∴能组成三角形,故本选项正确.
故选:D.
5.解:∵6﹣4<AB<6+4,
∴2<AB<10.
∴所以不可能是10cm.
故选:A.
6.解:如图,分别过点A、E作AM⊥BC、EF⊥DC;
则AM∥EF,
∴△ADM∽△EDF,=;
∵AE=DE,
∴AM=2EF(设EF为λ),
∴==2,而S△ABC=12cm2,
S△BCE=6cm2.
故选:B.
7.解:设a=4m,b=5m,c=6m,
∵S△ABC=S=aha=bhb=chc,
∴aha=bhb=chc=2S,
又∵a=4m,b=5m,c=6m,
∴ha:hb:hc=::=15:12:10.
故选:C.
8.解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:C.
9.解:∵D、E分别是边BC、AB的中点,AD、BF相交于G,
∴G为△ABC的重心,
∴AG=2DG,
∵AD=6,
∴AG=4,
故选:C.
二.填空题(共9小题)
10.解:如图,作DK∥AC,交BE于K,连接CF,
∴∠KDF=∠EAF,∠DKF=∠AEF,
∵点D是BC的中点,EC=2AE,
∴KD=EC=AE,
在△KDF和△EAF中
∴△KDF≌△EAF(ASA),
∴DF=AF,
∵△ABC的面积为24,
∴S△ADC=12,
∴S△AFC=S△DFC=6,
∵S△AEF=S△AFC=2,
∴S四边形DCEF=S△ADC﹣S△AEF=12﹣2=10.
故答案为:10.
11.解:∵△ABC中,∠C=40°,
∴∠A+∠B=180°﹣∠C=140°,
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣140°=220°,
故答案为:220°.
12.解;∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵∠B和∠C的平分线交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=×(∠ABC+∠ACB)=×130°=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°,
故答案为:115°.
13.解:如右图所示,
∵∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,
∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,
又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,
∴∠AHG+∠DNG+∠EGN=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.
14.解:∵AD是△ABC中BC边上的中线,
∴BD=DC=BC,
∴△ABD和△ADC的周长的差
=(AB+BC+AD)﹣(AC+BC+AD)
=AB﹣AC
=5﹣3
=2(cm).
故答案为:2.
15.解:∵点G为△ABC三边的重心,
∴AD是△ABC的中线,CF是△ABC的中线,AG=2GD,∴S△ABD=S△ABC=6,
∴S△ABG=2S△CBD=4,
∴S△BGF=2,
同理,S△CGE=2,
∴图中阴影部分的面积是4,
故答案为:4.
16.解:∵BD=DC,AE=EB,AD与CE相交于点O,
∴O是△ABC的重心,
∴AO=2DO=2×2=4cm.
故答案为:4.
17.解:∵∠2是△OBC的外角,
∴∠B+∠C=∠2,
∵∠1是△AEF的外角,
∴∠A+∠E=∠1,
∵∠1+∠2+∠D=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180.
18.解:解法一:根据图象,
∠1+∠2+∠3=(180°﹣∠ABC)+(180°﹣∠ACB)+(180°﹣∠BAC)=180°×3﹣180°=360°.
解法二:根据三角形的外角和,
∠1+∠2+∠3=360°.
三.解答题(共4小题)
19.解:(1)∵将△ACD沿AD折叠,点C恰好落在BC边上的点E处,
∴∠ADE=∠ADC=180°=90°,
故答案为:90°;
(2)由图形折叠的性质可得:∠AED=∠C=60°,
∵∠AED=∠B+∠BAE,
∴∠BAE=∠AED﹣∠B=60°﹣40°=20°.
20.证明:∵CE∥AB,
∴∠A=∠ACE∠B=∠DCE,
∵∠ACE+∠DCE+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
21.解:设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
则a=2×4=8(cm),
b=3×4=12(cm),
c=4×4=16(cm).
22.解:(1)∵在△ABD中,AD=BD,
∴∠B=∠BAD,
∵∠ADC=∠B+∠BAD,∠ADC=80°,
∴∠B=∠ADC=40°;
(2)△ABC是等腰三角形.
理由:∵∠B=40°,∠BAC=70°,
∴∠C=180°﹣∠B﹣∠BAC=70°,
∴∠C=∠BAC,
∴BA=BC,
∴△ABC是等腰三角形
一.选择题(共9小题)
1.如图,将一副直角三角板按如图所示叠放,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的大小是( )
A.10° B.15° C.25° D.30°
2.下列四组长度的小木棒中,按首尾顺次连接能组成一个三角形的是( )
A.1,2,3 B.4,5,6 C.3,4,12 D.4,8,4
3.若△ABC的三个内角的比为3:5:2,则△ABC是( )
A.等腰三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
4.下列长度的各组线段能组成一个三角形的是( )
A.1cm,2cm,3cm B.2cm,2cm,4cm
C.3cm,4cm,7cm D.3cm,3cm,4cm
5.如图,为估计池塘岸边两点A、B的距离,小方在池塘的一侧选取一点O,测得OA=6cm,OB=4cm,则点A、B间的距离不可能是( )
A.10 cm B.8cm C.6cm D.4cm
6.如图,△ABC的面积为12cm2,点D在BC边上,E是AD的中点,则△BCE的面积是( )
A.4cm2 B.6cm2 C.8cm2 D.10cm2
7.已知:a,b,c是△ABC的三边,且a:b:c=4:5:6,则它们的对应高ha:hb:hc的比是( )
A.4:5:6 B.6:5:4 C.15:12:10 D.10:12:15
8.人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.三角形具有稳定性
D.两直线平行,内错角相等
9.如图,在△ABC中,D,E分别是BC,AC的中点,AD和BE相交于点G,若AD=6,则AG的长度为( )
A.2 B.3 C.4 D.5
二.填空题(共9小题)
10.如图,在△ABC中,点D是BC的中点,点E是AC上一点,EC=2AE,已知S△ABC=24,那么S四边形DCEF= .
11.如图,在△ABC中,∠C=40°,按图中虚线将∠C剪去后,∠1+∠2等于 .
12.如图,在△ABC中,∠B和∠C的平分线交于点O,若∠A=50°,则∠BOC= .
13.如图,∠A+∠B+∠C+∠D+∠E+∠F= 度.
14.如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm,则△ABD与△ACD的周长之差为 cm.
15.如图,点G为△ABC三边的重心,若S△ABC=12,则图中阴影部分的面积是 .
16.如图,在△ABC中,BD=DC,AE=EB,AD与CE相交于点O,若DO=2cm,则AO= cm.
17.如图,∠A+∠B+∠C+∠D+∠E= 度.
18.如图所示:∠1+∠2+∠3= 度.
三.解答题(共4小题)
19.如图,在△ABC中,∠B=40°,∠C=60°,点D是BC边上的一点,将△ACD沿AD折叠,点C恰好落在BC边上的点E处.
(1)直接填空:∠ADE的大小是 ;
(2)求∠BAE的大小.
20.如图,点D是三角形ABC的边BC延长线上一点,CE∥AB,求证:∠A+∠B+∠ACB=180°.
21.一个三角形的周长为36cm,三边之比a:b:c=2:3:4,求a,b,c的值.
22.如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
参考答案
一.选择题(共9小题)
1.解:∵∠B=45°,
∴∠BAC=45°,
∴∠EAF=135°,
∴∠AFD=135°+30°=165°,
∴∠BFD=180°﹣∠AFD=15°
故选:B.
2.解:A、1+2=3,不满足三角形三边关系定理,故错误,不符合题意;
B、4+5>6,满足三边关系定理,故正确,符合题意;
C、3+4<12.不满足三边关系定理,故错误,不符合题意;
D、4+4=8.不满足三角形三边关系定理,故错误,不符合题意.
故选:B.
3.解:∵△ABC的三个内角的比为3:5:2可设此三角形的三个内角分别为2x,3x,5x,
∴2x+3x+5x=180°,解得x=18°,
∴5x=5×18°=90°.
∴此三角形是直角三角形.
故选:C.
4.解:A、∵1+2=3,∴不能组成三角形,故本选项错误;
B、∵2+2=4,∴不能组成三角形,故本选项错误;
C、∵3+4=7,∴不能组成三角形,故本选项错误;
D、∵4+5=9>6,∴能组成三角形,故本选项正确.
故选:D.
5.解:∵6﹣4<AB<6+4,
∴2<AB<10.
∴所以不可能是10cm.
故选:A.
6.解:如图,分别过点A、E作AM⊥BC、EF⊥DC;
则AM∥EF,
∴△ADM∽△EDF,=;
∵AE=DE,
∴AM=2EF(设EF为λ),
∴==2,而S△ABC=12cm2,
S△BCE=6cm2.
故选:B.
7.解:设a=4m,b=5m,c=6m,
∵S△ABC=S=aha=bhb=chc,
∴aha=bhb=chc=2S,
又∵a=4m,b=5m,c=6m,
∴ha:hb:hc=::=15:12:10.
故选:C.
8.解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:C.
9.解:∵D、E分别是边BC、AB的中点,AD、BF相交于G,
∴G为△ABC的重心,
∴AG=2DG,
∵AD=6,
∴AG=4,
故选:C.
二.填空题(共9小题)
10.解:如图,作DK∥AC,交BE于K,连接CF,
∴∠KDF=∠EAF,∠DKF=∠AEF,
∵点D是BC的中点,EC=2AE,
∴KD=EC=AE,
在△KDF和△EAF中
∴△KDF≌△EAF(ASA),
∴DF=AF,
∵△ABC的面积为24,
∴S△ADC=12,
∴S△AFC=S△DFC=6,
∵S△AEF=S△AFC=2,
∴S四边形DCEF=S△ADC﹣S△AEF=12﹣2=10.
故答案为:10.
11.解:∵△ABC中,∠C=40°,
∴∠A+∠B=180°﹣∠C=140°,
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣140°=220°,
故答案为:220°.
12.解;∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵∠B和∠C的平分线交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=×(∠ABC+∠ACB)=×130°=65°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=115°,
故答案为:115°.
13.解:如右图所示,
∵∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,
∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,
又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,
∴∠AHG+∠DNG+∠EGN=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.
14.解:∵AD是△ABC中BC边上的中线,
∴BD=DC=BC,
∴△ABD和△ADC的周长的差
=(AB+BC+AD)﹣(AC+BC+AD)
=AB﹣AC
=5﹣3
=2(cm).
故答案为:2.
15.解:∵点G为△ABC三边的重心,
∴AD是△ABC的中线,CF是△ABC的中线,AG=2GD,∴S△ABD=S△ABC=6,
∴S△ABG=2S△CBD=4,
∴S△BGF=2,
同理,S△CGE=2,
∴图中阴影部分的面积是4,
故答案为:4.
16.解:∵BD=DC,AE=EB,AD与CE相交于点O,
∴O是△ABC的重心,
∴AO=2DO=2×2=4cm.
故答案为:4.
17.解:∵∠2是△OBC的外角,
∴∠B+∠C=∠2,
∵∠1是△AEF的外角,
∴∠A+∠E=∠1,
∵∠1+∠2+∠D=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180.
18.解:解法一:根据图象,
∠1+∠2+∠3=(180°﹣∠ABC)+(180°﹣∠ACB)+(180°﹣∠BAC)=180°×3﹣180°=360°.
解法二:根据三角形的外角和,
∠1+∠2+∠3=360°.
三.解答题(共4小题)
19.解:(1)∵将△ACD沿AD折叠,点C恰好落在BC边上的点E处,
∴∠ADE=∠ADC=180°=90°,
故答案为:90°;
(2)由图形折叠的性质可得:∠AED=∠C=60°,
∵∠AED=∠B+∠BAE,
∴∠BAE=∠AED﹣∠B=60°﹣40°=20°.
20.证明:∵CE∥AB,
∴∠A=∠ACE∠B=∠DCE,
∵∠ACE+∠DCE+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
21.解:设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
则a=2×4=8(cm),
b=3×4=12(cm),
c=4×4=16(cm).
22.解:(1)∵在△ABD中,AD=BD,
∴∠B=∠BAD,
∵∠ADC=∠B+∠BAD,∠ADC=80°,
∴∠B=∠ADC=40°;
(2)△ABC是等腰三角形.
理由:∵∠B=40°,∠BAC=70°,
∴∠C=180°﹣∠B﹣∠BAC=70°,
∴∠C=∠BAC,
∴BA=BC,
∴△ABC是等腰三角形
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
