2021-2022学年浙教版八年级数学上册 1.5 三角形全等的判定 练习(word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册 1.5 三角形全等的判定 练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 15:26:15 | ||
图片预览

文档简介
11036300111887001.5《三角形全等的判定》同步练习题
一选择题
1.在△ABC中,已知AB=AC,D是BC的中点,则∠ADB是( )
A. 锐角 B. 钝角
C. 直角 D. 无法确定
2.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点;再分别以点E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的度数是( )
A. 20° B. 25° C. 30° D. 40°
3.在△ABC与△A1B1C1中,下列不能判定△ABC≌A1B1C1的是( )
A.AB=A1B1,BC=B1C1,∠B=∠B1
B.AB=A1B1,AC=A1C1,∠C=∠C1
C.∠B=∠B1,∠C=∠C1,BC=B1C1
D.AB=A1B1,BC=B1C1,AC=A1C1
4.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
(第4题)
A.甲和乙 B.乙和丙
C.只有乙 D.只有丙
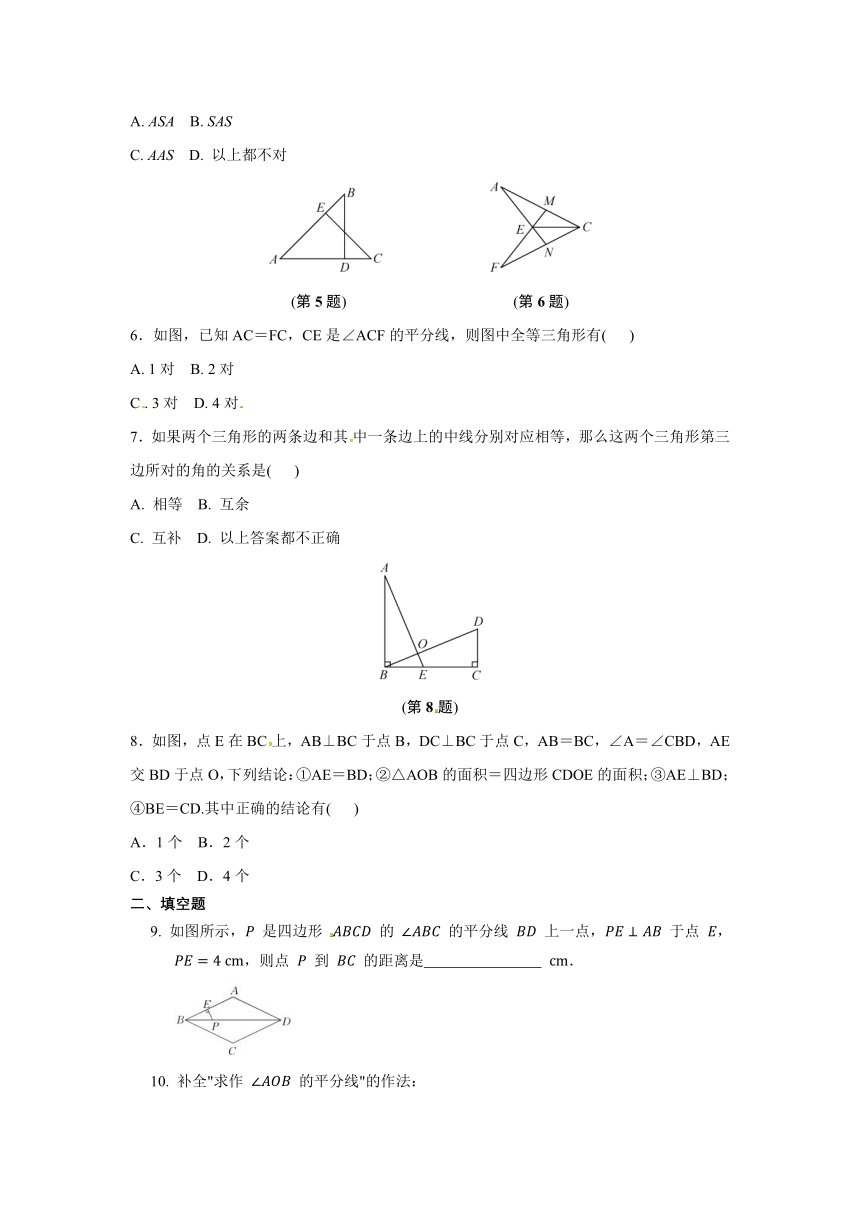
5.如图,已知BD⊥AC于点D,CE⊥AB于点E,BD=EC,则△ABD≌△ACE,其三角形全等的判定方法是( )
A. ASA B. SAS
C. AAS D. 以上都不对
(第5题) (第6题)
6.如图,已知AC=FC,CE是∠ACF的平分线,则图中全等三角形有( )
A. 1对 B. 2对
C. 3对 D. 4对
7.如果两个三角形的两条边和其中一条边上的中线分别对应相等,那么这两个三角形第三边所对的角的关系是( )
A. 相等 B. 互余
C. 互补 D. 以上答案都不正确
(第8题)
8.如图,点E在BC上,AB⊥BC于点B,DC⊥BC于点C,AB=BC,∠A=∠CBD,AE交BD于点O,下列结论:①AE=BD;②△AOB的面积=四边形CDOE的面积;③AE⊥BD;④BE=CD.其中正确的结论有( )
A.1个 B.2个
C.3个 D.4个
二、填空题
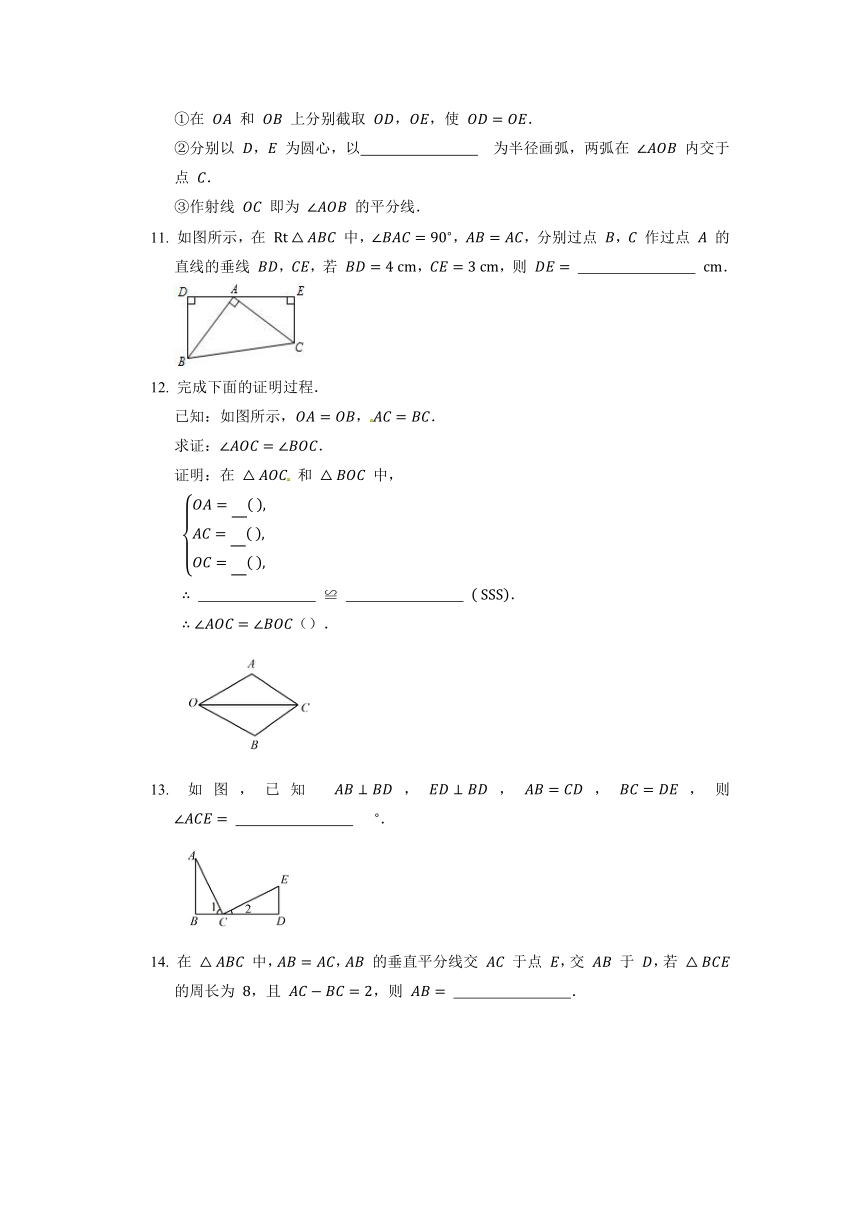
9. 如图所示,P 是四边形 ABCD 的 ∠ABC 的平分线 BD 上一点,PE⊥AB 于点 E,PE=4 cm,则点 P 到 BC 的距离是 ? cm.
10. 补全"求作 ∠AOB 的平分线"的作法:
①在 OA 和 OB 上分别截取 OD,OE,使 OD=OE.
②分别以 D,E 为圆心,以 ? 为半径画弧,两弧在 ∠AOB 内交于点 C.
③作射线 OC 即为 ∠AOB 的平分线.
11. 如图所示,在 Rt△ABC 中,∠BAC=90?,AB=AC,分别过点 B,C 作过点 A 的直线的垂线 BD,CE,若 BD=4 cm,CE=3 cm,则 DE= ? cm.
12. 完成下面的证明过程.
已知:如图所示,OA=OB,AC=BC.
求证:∠AOC=∠BOC.
证明:在 △AOC 和 △BOC 中,
OA=? ,AC=? ,OC=? ,
∴ ? ≌ ? SSS.
∴∠AOC=∠BOC().
13. 如图,已知 AB⊥BD,ED⊥BD,AB=CD,BC=DE,则 ∠ACE= ? ?.
14. 在 △ABC 中,AB=AC,AB 的垂直平分线交 AC 于点 E,交 AB 于 D,若 △BCE 的周长为 8,且 AC?BC=2,则 AB= ?.
15. 如图所示,已知 AE 平分 ∠BAC,BE⊥AE 于 E,ED∥AC,∠BAE=36?,那么 ∠BED= ?.
16. 如图,在 △ABC 中,∠C=90?,AD 平分 ∠BAC,AB=5,CD=2,则 △ABD 的面积是 ?.
三、简答题
17.如图,已知点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.试判断AC与DF是否平行,并说明理由.
(第17题)
18.如图,在Rt△ABC中,∠ACB=90°,点D,F分别在AB,AC上,CF=CB,连结CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连结EF.
(第18题)
(1)求证:△BCD≌△FCE.
(2)若EF∥CD,求∠BDC的度数.
19.如图,△ABC的两条角平分线BD,CE交于点O,∠A=60°.求证:CD+BE=BC.
(第19题)
20.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为F,且AB=ED.
(1)求证:BD=CB.
(2)若BD=8 cm,求AC的长.
(第20题)
参考答案
1-5CABBC
6-8DAD
9. 4
10. 大于 12DE 的长为半径
11. 7
12. OB;已知;BC;已知;OC;公共边;△AOC;△BOC;全等三角形的对应角相等
13. 90
14. 5
15. 126?
16. 5
17【解】 AC∥DF.理由如下:
∵BE=CF,∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∵
∴△ABC≌△DEF(SSS).
∴∠ACB=∠F(全等三角形的对应角相等).
∴AC∥DF(同位角相等,两直线平行).
18【解】 (1)∵将线段CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°.
∵∠ACB=90°,
∴∠BCD=90°-∠ACD=∠FCE.
在△BCD和△FCE中,∵
∴△BCD≌△FCE(SAS).
(2)∵△BCD≌△FCE,∴∠BDC=∠E.
∵EF∥CD,∴∠E=180°-∠DCE=90°,
∴∠BDC=90°.
19【解】 在BC上取一点F,使BF=BE,连结OF.
∵BD,CE分别平分∠ABC,∠ACB,∴∠ABD=∠CBD,∠ACE=∠BCE.
∵BE=BF,∠EBO=∠FBO,BO=BO,
∴△EBO≌△FBO(SAS),∴∠EOB=∠FOB.
∵∠A=60°,∴∠ABC+∠ACB=120°,
∴∠OBC+∠OCB=120°÷2=60°,
∴∠COB=120°,∴∠EOB=∠DOC=60°,
∴∠FOB=∠EOB=60°,
∴∠FOC=∠COB-∠FOB=60°,
∴∠FOC=∠DOC.
又∵OC=OC,∠FCO=∠DCO,
∴△OFC≌△ODC(ASA),∴CD=CF,
∴BC=BF+CF=BE+CD.[来源:
20【解】 (1)∵∠DBC=90°,∴∠ABC+∠DBF=90°.
∵DE⊥AB,
∴∠EDB+∠DBF=90°,
∴∠ABC=∠EDB.
在△EBD和△ACB中,
∵
∴△EBD≌△ACB(AAS),∴BD=CB.
(2)由(1)可知△EBD≌△ACB,∴EB=AC.
又∵E是BC的中点,∴EB=BC,
∴EB=BD=×8=4(cm),∴AC=4 cm.
一选择题
1.在△ABC中,已知AB=AC,D是BC的中点,则∠ADB是( )
A. 锐角 B. 钝角
C. 直角 D. 无法确定
2.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点;再分别以点E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的度数是( )
A. 20° B. 25° C. 30° D. 40°
3.在△ABC与△A1B1C1中,下列不能判定△ABC≌A1B1C1的是( )
A.AB=A1B1,BC=B1C1,∠B=∠B1
B.AB=A1B1,AC=A1C1,∠C=∠C1
C.∠B=∠B1,∠C=∠C1,BC=B1C1
D.AB=A1B1,BC=B1C1,AC=A1C1
4.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是( )
(第4题)
A.甲和乙 B.乙和丙
C.只有乙 D.只有丙
5.如图,已知BD⊥AC于点D,CE⊥AB于点E,BD=EC,则△ABD≌△ACE,其三角形全等的判定方法是( )
A. ASA B. SAS
C. AAS D. 以上都不对
(第5题) (第6题)
6.如图,已知AC=FC,CE是∠ACF的平分线,则图中全等三角形有( )
A. 1对 B. 2对
C. 3对 D. 4对
7.如果两个三角形的两条边和其中一条边上的中线分别对应相等,那么这两个三角形第三边所对的角的关系是( )
A. 相等 B. 互余
C. 互补 D. 以上答案都不正确
(第8题)
8.如图,点E在BC上,AB⊥BC于点B,DC⊥BC于点C,AB=BC,∠A=∠CBD,AE交BD于点O,下列结论:①AE=BD;②△AOB的面积=四边形CDOE的面积;③AE⊥BD;④BE=CD.其中正确的结论有( )
A.1个 B.2个
C.3个 D.4个
二、填空题
9. 如图所示,P 是四边形 ABCD 的 ∠ABC 的平分线 BD 上一点,PE⊥AB 于点 E,PE=4 cm,则点 P 到 BC 的距离是 ? cm.
10. 补全"求作 ∠AOB 的平分线"的作法:
①在 OA 和 OB 上分别截取 OD,OE,使 OD=OE.
②分别以 D,E 为圆心,以 ? 为半径画弧,两弧在 ∠AOB 内交于点 C.
③作射线 OC 即为 ∠AOB 的平分线.
11. 如图所示,在 Rt△ABC 中,∠BAC=90?,AB=AC,分别过点 B,C 作过点 A 的直线的垂线 BD,CE,若 BD=4 cm,CE=3 cm,则 DE= ? cm.
12. 完成下面的证明过程.
已知:如图所示,OA=OB,AC=BC.
求证:∠AOC=∠BOC.
证明:在 △AOC 和 △BOC 中,
OA=? ,AC=? ,OC=? ,
∴ ? ≌ ? SSS.
∴∠AOC=∠BOC().
13. 如图,已知 AB⊥BD,ED⊥BD,AB=CD,BC=DE,则 ∠ACE= ? ?.
14. 在 △ABC 中,AB=AC,AB 的垂直平分线交 AC 于点 E,交 AB 于 D,若 △BCE 的周长为 8,且 AC?BC=2,则 AB= ?.
15. 如图所示,已知 AE 平分 ∠BAC,BE⊥AE 于 E,ED∥AC,∠BAE=36?,那么 ∠BED= ?.
16. 如图,在 △ABC 中,∠C=90?,AD 平分 ∠BAC,AB=5,CD=2,则 △ABD 的面积是 ?.
三、简答题
17.如图,已知点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.试判断AC与DF是否平行,并说明理由.
(第17题)
18.如图,在Rt△ABC中,∠ACB=90°,点D,F分别在AB,AC上,CF=CB,连结CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连结EF.
(第18题)
(1)求证:△BCD≌△FCE.
(2)若EF∥CD,求∠BDC的度数.
19.如图,△ABC的两条角平分线BD,CE交于点O,∠A=60°.求证:CD+BE=BC.
(第19题)
20.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为F,且AB=ED.
(1)求证:BD=CB.
(2)若BD=8 cm,求AC的长.
(第20题)
参考答案
1-5CABBC
6-8DAD
9. 4
10. 大于 12DE 的长为半径
11. 7
12. OB;已知;BC;已知;OC;公共边;△AOC;△BOC;全等三角形的对应角相等
13. 90
14. 5
15. 126?
16. 5
17【解】 AC∥DF.理由如下:
∵BE=CF,∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∵
∴△ABC≌△DEF(SSS).
∴∠ACB=∠F(全等三角形的对应角相等).
∴AC∥DF(同位角相等,两直线平行).
18【解】 (1)∵将线段CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°.
∵∠ACB=90°,
∴∠BCD=90°-∠ACD=∠FCE.
在△BCD和△FCE中,∵
∴△BCD≌△FCE(SAS).
(2)∵△BCD≌△FCE,∴∠BDC=∠E.
∵EF∥CD,∴∠E=180°-∠DCE=90°,
∴∠BDC=90°.
19【解】 在BC上取一点F,使BF=BE,连结OF.
∵BD,CE分别平分∠ABC,∠ACB,∴∠ABD=∠CBD,∠ACE=∠BCE.
∵BE=BF,∠EBO=∠FBO,BO=BO,
∴△EBO≌△FBO(SAS),∴∠EOB=∠FOB.
∵∠A=60°,∴∠ABC+∠ACB=120°,
∴∠OBC+∠OCB=120°÷2=60°,
∴∠COB=120°,∴∠EOB=∠DOC=60°,
∴∠FOB=∠EOB=60°,
∴∠FOC=∠COB-∠FOB=60°,
∴∠FOC=∠DOC.
又∵OC=OC,∠FCO=∠DCO,
∴△OFC≌△ODC(ASA),∴CD=CF,
∴BC=BF+CF=BE+CD.[来源:
20【解】 (1)∵∠DBC=90°,∴∠ABC+∠DBF=90°.
∵DE⊥AB,
∴∠EDB+∠DBF=90°,
∴∠ABC=∠EDB.
在△EBD和△ACB中,
∵
∴△EBD≌△ACB(AAS),∴BD=CB.
(2)由(1)可知△EBD≌△ACB,∴EB=AC.
又∵E是BC的中点,∴EB=BC,
∴EB=BD=×8=4(cm),∴AC=4 cm.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
