2021—2022学年浙教版九年级数学上册 3.3垂径定理 第2课时 垂径定理的逆定理练习题 (word版含答案)
文档属性
| 名称 | 2021—2022学年浙教版九年级数学上册 3.3垂径定理 第2课时 垂径定理的逆定理练习题 (word版含答案) | 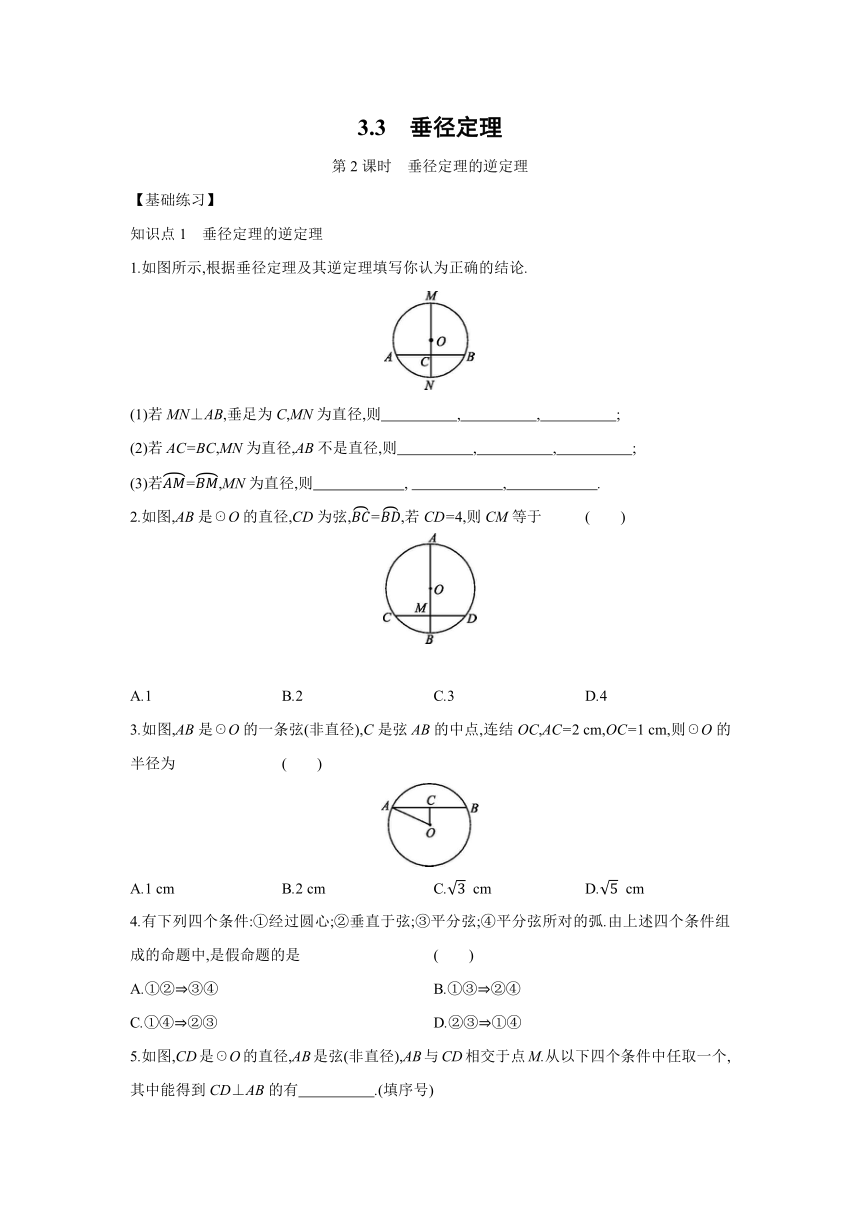 | |
| 格式 | docx | ||
| 文件大小 | 187.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 15:29:04 | ||
图片预览




文档简介
3.3 垂径定理
第2课时 垂径定理的逆定理
【基础练习】
知识点1 垂径定理的逆定理
1.如图所示,根据垂径定理及其逆定理填写你认为正确的结论.
(1)若MN⊥AB,垂足为C,MN为直径,则 , , ;?
(2)若AC=BC,MN为直径,AB不是直径,则 , , ;?
(3)若AM=BM,MN为直径,则 ,? , .?
2.如图,AB是☉O的直径,CD为弦,BC=BD,若CD=4,则CM等于 ( )
A.1 B.2 C.3 D.4
3.如图,AB是☉O的一条弦(非直径),C是弦AB的中点,连结OC,AC=2 cm,OC=1 cm,则☉O的半径为 ( )
A.1 cm B.2 cm C.3 cm D.5 cm
4.有下列四个条件:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四个条件组成的命题中,是假命题的是 ( )
A.①②?③④ B.①③?②④
C.①④?②③ D.②③?①④
5.如图,CD是☉O的直径,AB是弦(非直径),AB与CD相交于点M.从以下四个条件中任取一个,其中能得到CD⊥AB的有 .(填序号)?
①AM=BM;②OM=CM;③AC=BC;④AD=BD.
6.如图,☉O的两条弦AB∥CD(AB不是直径),E为AB的中点,连结EC,ED.
(1)直线EO与AB垂直吗?请说明理由;
(2)求证:EC=ED.
知识点2 垂径定理的逆定理的应用
7.如图,一条公路弯道处是一段圆弧AB,点O是这条弧所在圆的圆心,C是AB的中点,OC与AB相交于点D.已知AB=120 m,CD=20 m,那么这段弯道所在圆的半径为 ( )
A.200 m B.2003 m C.100 m D.1003 m
8.如图,在残破的圆形工件上量得一条弦AB=16,AB的中点C到AB的距离CD=4,求这个圆形工件的半径.
【能力提升】
9.有下列命题:(1)垂直于弦的直线平分弦;(2)平分弦的直径必垂直于弦,并且平分弦所对的两条弧;(3)平分弦的直线必过圆心;(4)弦所对的两条弧的中点连线垂直平分弦.其中正确的命题有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,☉O的直径AB与弦CD相交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为 ( )
A.23 B.4 C.43 D.8
11.如图,AB,AC是☉O的两条弦,M,N分别为AB,AC的中点,MN与AB,AC分别交于点E,F.判断△AEF的形状并给予证明.
12.如图,在☉O中,DE是☉O的直径,AB是☉O的弦,AB的中点C在直径DE上.已知AB=8 cm,CD=2 cm.
(1)求☉O的面积;
(2)连结AE,过圆心O向AE作垂线,垂足为F,求OF的长.
13.如图所示,隧道的截面由圆弧AED和矩形ABCD构成,矩形的长BC为12 m,宽AB为3 m,隧道的顶端E(圆弧AED的中点)高出道路(BC)7 m.
(1)求圆弧AED所在圆的半径;
(2)如果该隧道内设双行道,现有一辆货运卡车高6.5 m,宽2.3 m,那么这辆货运卡车能否通过该隧道?
答案
1.(1)AC=BC AN=BN AM=BM
(2)MN⊥AB AN=BN AM=BM
(3)AN=BN AC=BC MN⊥AB
[解析] (1)由垂径定理可知;
(2)由结论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧;
(3)平分弧的直径垂直平分弧所对的弦.
2.B
3.D
4.B [解析] 垂直于弦的直径平分弦,并且平分弦所对的弧;平分弧的直径垂直平分弧所对的弦;垂直平分弦的直线必过圆心,且平分弦所对的弧,故本题选B.
5.①③④
6.解:(1)直线EO与AB垂直.
理由:如图,连结EO并延长交CD于点F.
∵EO过点O,E为AB的中点,AB不是直径,
∴EO⊥AB.
(2)证明:∵EO⊥AB,AB∥CD,
∴EF⊥CD.
∵EF过点O,
∴CF=DF,
∴EC=ED.
7.C [解析] 如图,连结OA.
∵C是AB的中点,OC与AB相交于点D,
∴AB⊥OC,AD=12AB=12×120=60(m).
在Rt△AOD中,有OA2=AD2+OD2.
设OA=r m,则OD=r-CD=(r-20)m,
∴r2=602+(r-20)2,解得r=100.
8.解:∵CD⊥AB,C是AB的中点,
∴圆心在直线CD上.
设圆心为O,连结OB.
设☉O的半径为r,则OD=r-4.
∵OD⊥AB,∴BD=12AB=8.
在Rt△OBD中,OB2=OD2+BD2,即r2=(r-4)2+82,
解得r=10,故这个圆形工件的半径为10.
9.A [解析] (1)垂直于弦的直径平分弦,故本选项错误;
(2)平分弦(不是直径)的直径必垂直于弦,并且平分弦所对的两条弧,故本选项错误;
(3)垂直于弦且平分弦的直线必过圆心,故本选项错误;
(4)弦所对的两条弧的中点连线垂直平分弦,故本选项正确.则正确的命题有1个.故选A.
10.C [解析] ∵☉O的直径AB与弦CD相交于点E,且CE=DE,∴AB⊥CD.
∵∠A=30°,OA=OC,
∴∠A=∠ACO=30°,∴∠COB=60°,
∴OE=12OC=2,∴CE=42-22=23,
∴CD=43.故选C.
11.解:△AEF是等腰三角形.
证明:如图,连结OM,ON,分别交AB,AC于点P,Q.
∵M,N分别为AB,AC的中点,
∴OM⊥AB,ON⊥AC,
∴∠MPE=∠NQF=90°,
∴∠PEM=90°-∠M,∠QFN=90°-∠N.
∵OM=ON,
∴∠M=∠N,
∴∠PEM=∠QFN.
又∵∠AEF=∠PEM,∠AFE=∠QFN,
∴∠AEF=∠AFE,
∴AE=AF,
即△AEF是等腰三角形.
12.解:(1)连结OA,如图所示.
∵C为AB的中点,AB=8 cm,
∴AC=4 cm,AB⊥DE.
设☉O的半径为r cm,则OC=(r-2)cm.
在Rt△OAC中,由勾股定理,得OC2+AC2=OA2,即(r-2)2+42=r2,
解得r=5,
∴☉O的面积=πr2=π×25=25π(cm2).
(2)∵OC=OD-CD=5-2=3(cm),
∴EC=EO+OC=5+3=8(cm),
∴AE=AC2+EC2=42+82=45(cm).
∵OF⊥AE,
∴EF=12AE=12×45=25(cm),
∴OF=EO2-EF2=25-20=5(cm).
13.解:(1)如图①,设圆弧AED所在圆的圆心为O,半径为R m,连结OE交AD于点F,连结OA,OD.
由垂径定理的逆定理,得OF垂直平分AD,所以AF=6 m,OF=R-(7-3)=(R-4)m.
在Rt△AOF中,由勾股定理,得AF2+OF2=OA2,
即62+(R-4)2=R2,
解得R=6.5,
即圆弧AED所在圆的半径为6.5 m.
(2)如图②,在ED上取点H,过点H作HG⊥OE于点G,且GH=2.3 m.
由(1)知,圆弧AED所在圆的半径OH=6.5 m.
在Rt△OGH中,由勾股定理,得OG=6.52-2.32≈6.08(m),
所以点G与BC的距离约为7-6.5+6.08=6.58(m)>6.5 m,
故这辆货运卡车能通过该隧道.
第2课时 垂径定理的逆定理
【基础练习】
知识点1 垂径定理的逆定理
1.如图所示,根据垂径定理及其逆定理填写你认为正确的结论.
(1)若MN⊥AB,垂足为C,MN为直径,则 , , ;?
(2)若AC=BC,MN为直径,AB不是直径,则 , , ;?
(3)若AM=BM,MN为直径,则 ,? , .?
2.如图,AB是☉O的直径,CD为弦,BC=BD,若CD=4,则CM等于 ( )
A.1 B.2 C.3 D.4
3.如图,AB是☉O的一条弦(非直径),C是弦AB的中点,连结OC,AC=2 cm,OC=1 cm,则☉O的半径为 ( )
A.1 cm B.2 cm C.3 cm D.5 cm
4.有下列四个条件:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的弧.由上述四个条件组成的命题中,是假命题的是 ( )
A.①②?③④ B.①③?②④
C.①④?②③ D.②③?①④
5.如图,CD是☉O的直径,AB是弦(非直径),AB与CD相交于点M.从以下四个条件中任取一个,其中能得到CD⊥AB的有 .(填序号)?
①AM=BM;②OM=CM;③AC=BC;④AD=BD.
6.如图,☉O的两条弦AB∥CD(AB不是直径),E为AB的中点,连结EC,ED.
(1)直线EO与AB垂直吗?请说明理由;
(2)求证:EC=ED.
知识点2 垂径定理的逆定理的应用
7.如图,一条公路弯道处是一段圆弧AB,点O是这条弧所在圆的圆心,C是AB的中点,OC与AB相交于点D.已知AB=120 m,CD=20 m,那么这段弯道所在圆的半径为 ( )
A.200 m B.2003 m C.100 m D.1003 m
8.如图,在残破的圆形工件上量得一条弦AB=16,AB的中点C到AB的距离CD=4,求这个圆形工件的半径.
【能力提升】
9.有下列命题:(1)垂直于弦的直线平分弦;(2)平分弦的直径必垂直于弦,并且平分弦所对的两条弧;(3)平分弦的直线必过圆心;(4)弦所对的两条弧的中点连线垂直平分弦.其中正确的命题有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图,☉O的直径AB与弦CD相交于点E,且CE=DE,∠A=30°,OC=4,那么CD的长为 ( )
A.23 B.4 C.43 D.8
11.如图,AB,AC是☉O的两条弦,M,N分别为AB,AC的中点,MN与AB,AC分别交于点E,F.判断△AEF的形状并给予证明.
12.如图,在☉O中,DE是☉O的直径,AB是☉O的弦,AB的中点C在直径DE上.已知AB=8 cm,CD=2 cm.
(1)求☉O的面积;
(2)连结AE,过圆心O向AE作垂线,垂足为F,求OF的长.
13.如图所示,隧道的截面由圆弧AED和矩形ABCD构成,矩形的长BC为12 m,宽AB为3 m,隧道的顶端E(圆弧AED的中点)高出道路(BC)7 m.
(1)求圆弧AED所在圆的半径;
(2)如果该隧道内设双行道,现有一辆货运卡车高6.5 m,宽2.3 m,那么这辆货运卡车能否通过该隧道?
答案
1.(1)AC=BC AN=BN AM=BM
(2)MN⊥AB AN=BN AM=BM
(3)AN=BN AC=BC MN⊥AB
[解析] (1)由垂径定理可知;
(2)由结论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧;
(3)平分弧的直径垂直平分弧所对的弦.
2.B
3.D
4.B [解析] 垂直于弦的直径平分弦,并且平分弦所对的弧;平分弧的直径垂直平分弧所对的弦;垂直平分弦的直线必过圆心,且平分弦所对的弧,故本题选B.
5.①③④
6.解:(1)直线EO与AB垂直.
理由:如图,连结EO并延长交CD于点F.
∵EO过点O,E为AB的中点,AB不是直径,
∴EO⊥AB.
(2)证明:∵EO⊥AB,AB∥CD,
∴EF⊥CD.
∵EF过点O,
∴CF=DF,
∴EC=ED.
7.C [解析] 如图,连结OA.
∵C是AB的中点,OC与AB相交于点D,
∴AB⊥OC,AD=12AB=12×120=60(m).
在Rt△AOD中,有OA2=AD2+OD2.
设OA=r m,则OD=r-CD=(r-20)m,
∴r2=602+(r-20)2,解得r=100.
8.解:∵CD⊥AB,C是AB的中点,
∴圆心在直线CD上.
设圆心为O,连结OB.
设☉O的半径为r,则OD=r-4.
∵OD⊥AB,∴BD=12AB=8.
在Rt△OBD中,OB2=OD2+BD2,即r2=(r-4)2+82,
解得r=10,故这个圆形工件的半径为10.
9.A [解析] (1)垂直于弦的直径平分弦,故本选项错误;
(2)平分弦(不是直径)的直径必垂直于弦,并且平分弦所对的两条弧,故本选项错误;
(3)垂直于弦且平分弦的直线必过圆心,故本选项错误;
(4)弦所对的两条弧的中点连线垂直平分弦,故本选项正确.则正确的命题有1个.故选A.
10.C [解析] ∵☉O的直径AB与弦CD相交于点E,且CE=DE,∴AB⊥CD.
∵∠A=30°,OA=OC,
∴∠A=∠ACO=30°,∴∠COB=60°,
∴OE=12OC=2,∴CE=42-22=23,
∴CD=43.故选C.
11.解:△AEF是等腰三角形.
证明:如图,连结OM,ON,分别交AB,AC于点P,Q.
∵M,N分别为AB,AC的中点,
∴OM⊥AB,ON⊥AC,
∴∠MPE=∠NQF=90°,
∴∠PEM=90°-∠M,∠QFN=90°-∠N.
∵OM=ON,
∴∠M=∠N,
∴∠PEM=∠QFN.
又∵∠AEF=∠PEM,∠AFE=∠QFN,
∴∠AEF=∠AFE,
∴AE=AF,
即△AEF是等腰三角形.
12.解:(1)连结OA,如图所示.
∵C为AB的中点,AB=8 cm,
∴AC=4 cm,AB⊥DE.
设☉O的半径为r cm,则OC=(r-2)cm.
在Rt△OAC中,由勾股定理,得OC2+AC2=OA2,即(r-2)2+42=r2,
解得r=5,
∴☉O的面积=πr2=π×25=25π(cm2).
(2)∵OC=OD-CD=5-2=3(cm),
∴EC=EO+OC=5+3=8(cm),
∴AE=AC2+EC2=42+82=45(cm).
∵OF⊥AE,
∴EF=12AE=12×45=25(cm),
∴OF=EO2-EF2=25-20=5(cm).
13.解:(1)如图①,设圆弧AED所在圆的圆心为O,半径为R m,连结OE交AD于点F,连结OA,OD.
由垂径定理的逆定理,得OF垂直平分AD,所以AF=6 m,OF=R-(7-3)=(R-4)m.
在Rt△AOF中,由勾股定理,得AF2+OF2=OA2,
即62+(R-4)2=R2,
解得R=6.5,
即圆弧AED所在圆的半径为6.5 m.
(2)如图②,在ED上取点H,过点H作HG⊥OE于点G,且GH=2.3 m.
由(1)知,圆弧AED所在圆的半径OH=6.5 m.
在Rt△OGH中,由勾股定理,得OG=6.52-2.32≈6.08(m),
所以点G与BC的距离约为7-6.5+6.08=6.58(m)>6.5 m,
故这辆货运卡车能通过该隧道.
同课章节目录
