4.2 由平行线截得的比例线段同步练习(含解析)
文档属性
| 名称 | 4.2 由平行线截得的比例线段同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 11:00:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级上
4.2由平行线截得的比例线段同步练习
一.选择题
1.(2021?醴陵市模拟)如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2
B.
C.1
D.
2.(2021?温岭市模拟)如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,则BC:CE=( )
A.3:5
B.1:3
C.5:3
D.2:3
3.(2021?拱墅区模拟)如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若,DE=4,则DF的长为( )
A.10
B.
C.12
D.14
4.(2020秋?开封期末)如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:4,那么CF:BF的值为( )
A.4:3
B.3:7
C.3:4
D.2:4
5.(2020秋?成华区期末)如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A.
B.
C.
D.
6.(2021?松北区模拟)如图,△ABC中,DE∥BC,GF∥AC,下列式子错误的是( )
A.
B.
C.
D.
7.(2020秋?龙华区期末)如图,已知直线l1∥l2∥l3,直线AC分别与直线l1,l2,l3,交于A、B、C三点,直线DF分别与直线l1,l2,l3交于D、E、F三点,AC与DF交于点O,若BC=2AO=2OB,OD=1.则OF的长是( )
A.1
B.2
C.3
D.4
二.填空题
8.(2021?洪泽区二模)如图,l1∥l2∥l3,AC交l1、l2、l3分别于A、B、C,且AC=6,BC=4,DF交l1、l2、l3分别于D、E、F,则=
.
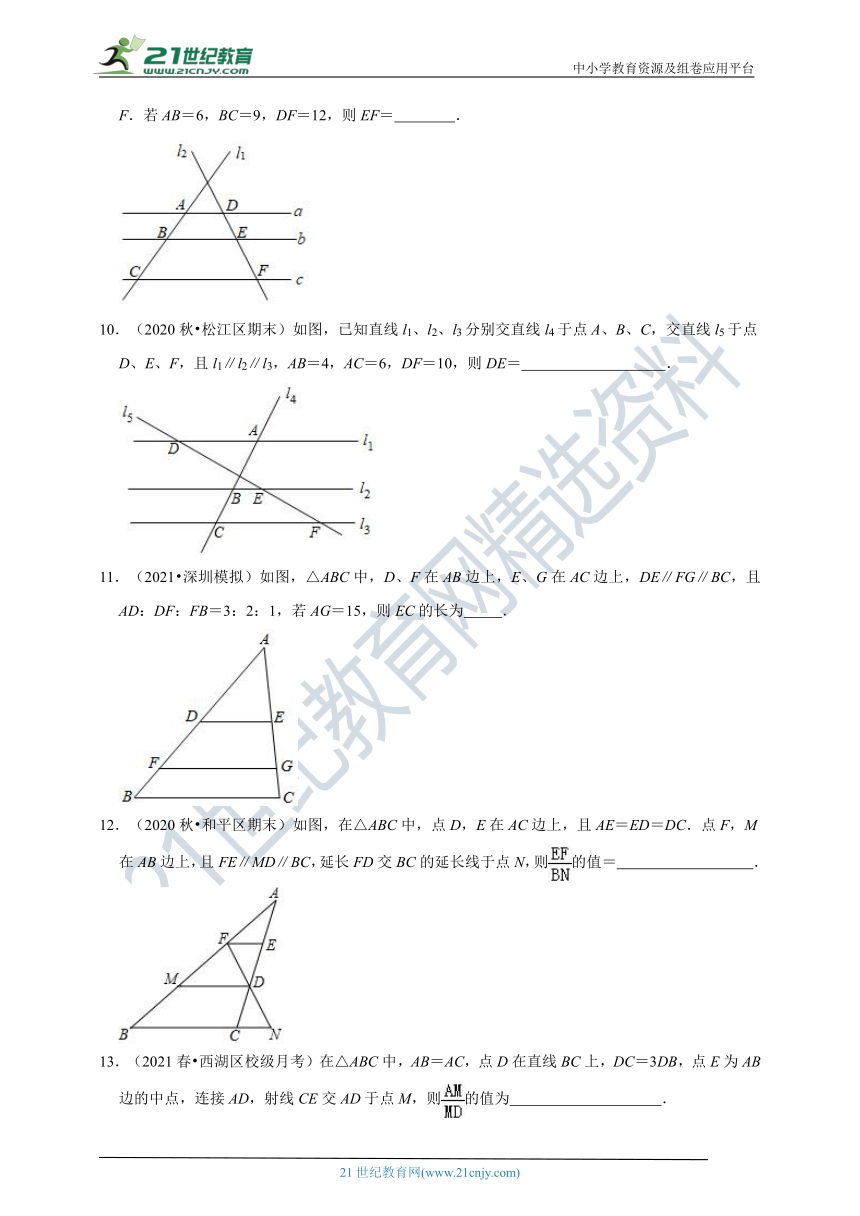
9.(2021?铁岭模拟)如图,a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB=6,BC=9,DF=12,则EF=
.
10.(2020秋?松江区期末)如图,已知直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,AB=4,AC=6,DF=10,则DE=
.
11.(2021?深圳模拟)如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为
.
12.(2020秋?和平区期末)如图,在△ABC中,点D,E在AC边上,且AE=ED=DC.点F,M在AB边上,且FE∥MD∥BC,延长FD交BC的延长线于点N,则的值=
.
13.(2021春?西湖区校级月考)在△ABC中,AB=AC,点D在直线BC上,DC=3DB,点E为AB边的中点,连接AD,射线CE交AD于点M,则的值为
.
三.解答题
14.(2021春?津南区月考)如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
15.(2020秋?兰州期中)如图,已知AC∥FE∥BD,求证:+=1.
16.(2019?下城区二模)如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
17.(2019?南京一模)下面是一位同学的一道作图题:
已知线段a、b、c(如图),求作线段x,使a:b=c:x
他的作法如下:
①以点O为端点画射线OM,ON.
②在OM上依次截取OA=a,AB=b.
③在ON上截取OC=c.
④连接AC,过点B作BD∥AC,交ON于点D.
(1)请根据这位同学的作图过程,在方框中用直尺和圆规画出图形(保留作图痕迹);
(2)请指出在所画的图形中,哪条线段是求作线段x,并说明理由;
(3)如果OA=4,AB=5,AC=3,求BD的长.
答案与解析
一.选择题
1.(2021?醴陵市模拟)如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2
B.
C.1
D.
【解析】解:∵直线l1∥l2∥l3,
∴=,
∵AB=2,BC=3,EF=2,
∴=,
∴DE=,
故选:B.
2.(2021?温岭市模拟)如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,则BC:CE=( )
A.3:5
B.1:3
C.5:3
D.2:3
【解析】解:∵AB∥CD∥EF,
∴===.
故选:A.
3.(2021?拱墅区模拟)如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若,DE=4,则DF的长为( )
A.10
B.
C.12
D.14
【解析】解:∵l1∥l2∥l3,
∴==,
∵DE=4,
∴EF=10,
∴DF=DE+EF=4+10=14,
故选:D.
4.(2020秋?开封期末)如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:4,那么CF:BF的值为( )
A.4:3
B.3:7
C.3:4
D.2:4
【解析】解:∵DE∥BC,EF∥AB,AD:DB=3:4,
∴,
∴,
故选:A.
5.(2020秋?成华区期末)如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A.
B.
C.
D.
【解析】解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==
故选:C.
6.(2021?松北区模拟)如图,△ABC中,DE∥BC,GF∥AC,下列式子错误的是( )
A.
B.
C.
D.
【解析】解:∵DE∥BC,GF∥AC,
∴△ADE∽△ABC,△BGF∽△BAC,△DGM∽△DAE,且四边形MECF是平行四边形.
∴=,=,=,ME=FC.
∴=.
所以ABD正确,C错误.
故选:C.
7.(2020秋?龙华区期末)如图,已知直线l1∥l2∥l3,直线AC分别与直线l1,l2,l3,交于A、B、C三点,直线DF分别与直线l1,l2,l3交于D、E、F三点,AC与DF交于点O,若BC=2AO=2OB,OD=1.则OF的长是( )
A.1
B.2
C.3
D.4
【解析】解:∵BC=2AO=2OB,
∴OC=3AO,
∵直线l1∥l2∥l3,
∴,
∴=,
∵OD=1,
∴OF=3,
故选:C.
二.填空题
8.(2021?洪泽区二模)如图,l1∥l2∥l3,AC交l1、l2、l3分别于A、B、C,且AC=6,BC=4,DF交l1、l2、l3分别于D、E、F,则= .
【解析】解:∵AC=6,BC=4,
∴AB=AC﹣BC=2,
∵l1∥l2∥l3,
∴==,
故答案为:.
9.(2021?铁岭模拟)如图,a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB=6,BC=9,DF=12,则EF= 7.2 .
【解析】解:∵a∥b∥c,
∴=,即=,
解得,EF=7.2,
故答案为:7.2.
10.(2020秋?松江区期末)如图,已知直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,AB=4,AC=6,DF=10,则DE= .
【解析】解:∵l1∥l2∥l3,
∴=,即=,
∴DE=.
故答案为.
11.(2021?深圳模拟)如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为 9 .
【解析】解:∵DE∥FG∥BC,
∴AD:DF:FB=AE:EG:GC,
∵AD:DF:FB=3:2:1,
∴AE:EG:GC=3:2:1,
设AE=3x,EG=2x,GC=x,
∵AG=15,
∴3x+2x=15,
解得:x=3,
即AE=9,EG=6,GC=3,
∴EC=EG+GC=6+3=9,
故答案为:9.
12.(2020秋?和平区期末)如图,在△ABC中,点D,E在AC边上,且AE=ED=DC.点F,M在AB边上,且FE∥MD∥BC,延长FD交BC的延长线于点N,则的值= .
【解析】解:∵EF∥DM∥BC,AE=DE=CD,
∴,
在△EFD与△CND中,
,
∴△EFD≌△CND(AAS),
∴EF=CN,
∵CN:BC=1:3,
∴CN:BN=1:4,
∴,
故答案为.
13.(2021春?西湖区校级月考)在△ABC中,AB=AC,点D在直线BC上,DC=3DB,点E为AB边的中点,连接AD,射线CE交AD于点M,则的值为 或 .
【解析】解:如图1,
过E作EQ∥BC,
设EQ=a,则BD=2a,DC=6a,
设QM=x,则MD=6x,AQ=7x,
∴AM=8x,MD=6x,
∴,
如图2,
过E作EH∥BC,过M作MP∥BC,
∵DC=3BD,
设BD=a,则DC=3a,BC=2a,
∴===,
∴=
∴=,
∴=,
∴=,
∴==,
∴=
故答案为:或.
三.解答题
14.(2021春?津南区月考)如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
【解析】解:∵l2∥l3,
∴=,
而AG=4,AB=2BC,
∴=2,
∴GF=2(cm);
∴AF=AG+GF=4cm+2cm=6cm;
∵l1∥l2∥l3,
∴=,即=,
∴EF=(cm).
答:GF,AF,EF的长分别为2cm,6cm,cm.
15.(2020秋?兰州期中)如图,已知AC∥FE∥BD,求证:+=1.
【解析】证明:∵AC∥EF,
∴,
∵FE∥BD,
∴,
①+②,得:,
即.
16.(2019?下城区二模)如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
【解析】解:(1)∵l1∥l2∥l3,
∴,
即,
解得:AC=12;
(2)∵l1∥l2∥l3,
∴,
∵AB=4,AC=12,
∴BC=8,
∴OB=2,
∴.
17.(2019?南京一模)下面是一位同学的一道作图题:
已知线段a、b、c(如图),求作线段x,使a:b=c:x
他的作法如下:
①以点O为端点画射线OM,ON.
②在OM上依次截取OA=a,AB=b.
③在ON上截取OC=c.
④连接AC,过点B作BD∥AC,交ON于点D.
(1)请根据这位同学的作图过程,在方框中用直尺和圆规画出图形(保留作图痕迹);
(2)请指出在所画的图形中,哪条线段是求作线段x,并说明理由;
(3)如果OA=4,AB=5,AC=3,求BD的长.
【解析】解:(1)如图所示;
(2)CD是所求作的线段x;
∵AC∥BD
∴=
即=.
(3)∵AC∥BD
∴△OAC∽△OBD
∴=
即=
∴BD=.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版九年级上
4.2由平行线截得的比例线段同步练习
一.选择题
1.(2021?醴陵市模拟)如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2
B.
C.1
D.
2.(2021?温岭市模拟)如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,则BC:CE=( )
A.3:5
B.1:3
C.5:3
D.2:3
3.(2021?拱墅区模拟)如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若,DE=4,则DF的长为( )
A.10
B.
C.12
D.14
4.(2020秋?开封期末)如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:4,那么CF:BF的值为( )
A.4:3
B.3:7
C.3:4
D.2:4
5.(2020秋?成华区期末)如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A.
B.
C.
D.
6.(2021?松北区模拟)如图,△ABC中,DE∥BC,GF∥AC,下列式子错误的是( )
A.
B.
C.
D.
7.(2020秋?龙华区期末)如图,已知直线l1∥l2∥l3,直线AC分别与直线l1,l2,l3,交于A、B、C三点,直线DF分别与直线l1,l2,l3交于D、E、F三点,AC与DF交于点O,若BC=2AO=2OB,OD=1.则OF的长是( )
A.1
B.2
C.3
D.4
二.填空题
8.(2021?洪泽区二模)如图,l1∥l2∥l3,AC交l1、l2、l3分别于A、B、C,且AC=6,BC=4,DF交l1、l2、l3分别于D、E、F,则=
.
9.(2021?铁岭模拟)如图,a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB=6,BC=9,DF=12,则EF=
.
10.(2020秋?松江区期末)如图,已知直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,AB=4,AC=6,DF=10,则DE=
.
11.(2021?深圳模拟)如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为
.
12.(2020秋?和平区期末)如图,在△ABC中,点D,E在AC边上,且AE=ED=DC.点F,M在AB边上,且FE∥MD∥BC,延长FD交BC的延长线于点N,则的值=
.
13.(2021春?西湖区校级月考)在△ABC中,AB=AC,点D在直线BC上,DC=3DB,点E为AB边的中点,连接AD,射线CE交AD于点M,则的值为
.
三.解答题
14.(2021春?津南区月考)如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
15.(2020秋?兰州期中)如图,已知AC∥FE∥BD,求证:+=1.
16.(2019?下城区二模)如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
17.(2019?南京一模)下面是一位同学的一道作图题:
已知线段a、b、c(如图),求作线段x,使a:b=c:x
他的作法如下:
①以点O为端点画射线OM,ON.
②在OM上依次截取OA=a,AB=b.
③在ON上截取OC=c.
④连接AC,过点B作BD∥AC,交ON于点D.
(1)请根据这位同学的作图过程,在方框中用直尺和圆规画出图形(保留作图痕迹);
(2)请指出在所画的图形中,哪条线段是求作线段x,并说明理由;
(3)如果OA=4,AB=5,AC=3,求BD的长.
答案与解析
一.选择题
1.(2021?醴陵市模拟)如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2
B.
C.1
D.
【解析】解:∵直线l1∥l2∥l3,
∴=,
∵AB=2,BC=3,EF=2,
∴=,
∴DE=,
故选:B.
2.(2021?温岭市模拟)如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,则BC:CE=( )
A.3:5
B.1:3
C.5:3
D.2:3
【解析】解:∵AB∥CD∥EF,
∴===.
故选:A.
3.(2021?拱墅区模拟)如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和D,E,F.若,DE=4,则DF的长为( )
A.10
B.
C.12
D.14
【解析】解:∵l1∥l2∥l3,
∴==,
∵DE=4,
∴EF=10,
∴DF=DE+EF=4+10=14,
故选:D.
4.(2020秋?开封期末)如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:4,那么CF:BF的值为( )
A.4:3
B.3:7
C.3:4
D.2:4
【解析】解:∵DE∥BC,EF∥AB,AD:DB=3:4,
∴,
∴,
故选:A.
5.(2020秋?成华区期末)如图,在平行四边形ABCD中,点F是AD上的点,AF=2FD,直线BF交AC于点E,交CD的延长线于点G,则的值为( )
A.
B.
C.
D.
【解析】解:由AF=2DF,可以假设DF=k,则AF=2k,AD=3k,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC=3k,
∴==,
∴==
故选:C.
6.(2021?松北区模拟)如图,△ABC中,DE∥BC,GF∥AC,下列式子错误的是( )
A.
B.
C.
D.
【解析】解:∵DE∥BC,GF∥AC,
∴△ADE∽△ABC,△BGF∽△BAC,△DGM∽△DAE,且四边形MECF是平行四边形.
∴=,=,=,ME=FC.
∴=.
所以ABD正确,C错误.
故选:C.
7.(2020秋?龙华区期末)如图,已知直线l1∥l2∥l3,直线AC分别与直线l1,l2,l3,交于A、B、C三点,直线DF分别与直线l1,l2,l3交于D、E、F三点,AC与DF交于点O,若BC=2AO=2OB,OD=1.则OF的长是( )
A.1
B.2
C.3
D.4
【解析】解:∵BC=2AO=2OB,
∴OC=3AO,
∵直线l1∥l2∥l3,
∴,
∴=,
∵OD=1,
∴OF=3,
故选:C.
二.填空题
8.(2021?洪泽区二模)如图,l1∥l2∥l3,AC交l1、l2、l3分别于A、B、C,且AC=6,BC=4,DF交l1、l2、l3分别于D、E、F,则= .
【解析】解:∵AC=6,BC=4,
∴AB=AC﹣BC=2,
∵l1∥l2∥l3,
∴==,
故答案为:.
9.(2021?铁岭模拟)如图,a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB=6,BC=9,DF=12,则EF= 7.2 .
【解析】解:∵a∥b∥c,
∴=,即=,
解得,EF=7.2,
故答案为:7.2.
10.(2020秋?松江区期末)如图,已知直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,AB=4,AC=6,DF=10,则DE= .
【解析】解:∵l1∥l2∥l3,
∴=,即=,
∴DE=.
故答案为.
11.(2021?深圳模拟)如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为 9 .
【解析】解:∵DE∥FG∥BC,
∴AD:DF:FB=AE:EG:GC,
∵AD:DF:FB=3:2:1,
∴AE:EG:GC=3:2:1,
设AE=3x,EG=2x,GC=x,
∵AG=15,
∴3x+2x=15,
解得:x=3,
即AE=9,EG=6,GC=3,
∴EC=EG+GC=6+3=9,
故答案为:9.
12.(2020秋?和平区期末)如图,在△ABC中,点D,E在AC边上,且AE=ED=DC.点F,M在AB边上,且FE∥MD∥BC,延长FD交BC的延长线于点N,则的值= .
【解析】解:∵EF∥DM∥BC,AE=DE=CD,
∴,
在△EFD与△CND中,
,
∴△EFD≌△CND(AAS),
∴EF=CN,
∵CN:BC=1:3,
∴CN:BN=1:4,
∴,
故答案为.
13.(2021春?西湖区校级月考)在△ABC中,AB=AC,点D在直线BC上,DC=3DB,点E为AB边的中点,连接AD,射线CE交AD于点M,则的值为 或 .
【解析】解:如图1,
过E作EQ∥BC,
设EQ=a,则BD=2a,DC=6a,
设QM=x,则MD=6x,AQ=7x,
∴AM=8x,MD=6x,
∴,
如图2,
过E作EH∥BC,过M作MP∥BC,
∵DC=3BD,
设BD=a,则DC=3a,BC=2a,
∴===,
∴=
∴=,
∴=,
∴=,
∴==,
∴=
故答案为:或.
三.解答题
14.(2021春?津南区月考)如图所示,l1∥l2∥l3,且AB=2BC,DF=5cm,AG=4cm.求GF,AF,EF的长.
【解析】解:∵l2∥l3,
∴=,
而AG=4,AB=2BC,
∴=2,
∴GF=2(cm);
∴AF=AG+GF=4cm+2cm=6cm;
∵l1∥l2∥l3,
∴=,即=,
∴EF=(cm).
答:GF,AF,EF的长分别为2cm,6cm,cm.
15.(2020秋?兰州期中)如图,已知AC∥FE∥BD,求证:+=1.
【解析】证明:∵AC∥EF,
∴,
∵FE∥BD,
∴,
①+②,得:,
即.
16.(2019?下城区二模)如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
【解析】解:(1)∵l1∥l2∥l3,
∴,
即,
解得:AC=12;
(2)∵l1∥l2∥l3,
∴,
∵AB=4,AC=12,
∴BC=8,
∴OB=2,
∴.
17.(2019?南京一模)下面是一位同学的一道作图题:
已知线段a、b、c(如图),求作线段x,使a:b=c:x
他的作法如下:
①以点O为端点画射线OM,ON.
②在OM上依次截取OA=a,AB=b.
③在ON上截取OC=c.
④连接AC,过点B作BD∥AC,交ON于点D.
(1)请根据这位同学的作图过程,在方框中用直尺和圆规画出图形(保留作图痕迹);
(2)请指出在所画的图形中,哪条线段是求作线段x,并说明理由;
(3)如果OA=4,AB=5,AC=3,求BD的长.
【解析】解:(1)如图所示;
(2)CD是所求作的线段x;
∵AC∥BD
∴=
即=.
(3)∵AC∥BD
∴△OAC∽△OBD
∴=
即=
∴BD=.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
