4.3 相似三角形同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级上
4.3相似三角形同步练习
一.选择题
1.(2021?鄞州区模拟)如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2
B.
C.
D.4
2.(2020秋?上虞区期末)如图,已知△ABC∽△A′B′C′,则图中角度α和边长x分别为( )
A.40°,9
B.40°,6
C.30°,9
D.30°,6
3.(2020秋?沂南县期末)如图,△ABC∽△DCA,∠B=33°,∠D=117°,则∠BAD的度数是( )
A.150°
B.147°
C.135°
D.120°
4.(2020秋?济南期末)如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
A.2
B.3
C.4
D.6
5.(2021?河池模拟)要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为4厘米,6厘米和9厘米,另一个三角形的最长边是18厘米,则它的最短边是( )
A.2厘米
B.4厘米
C.8厘米
D.12厘米
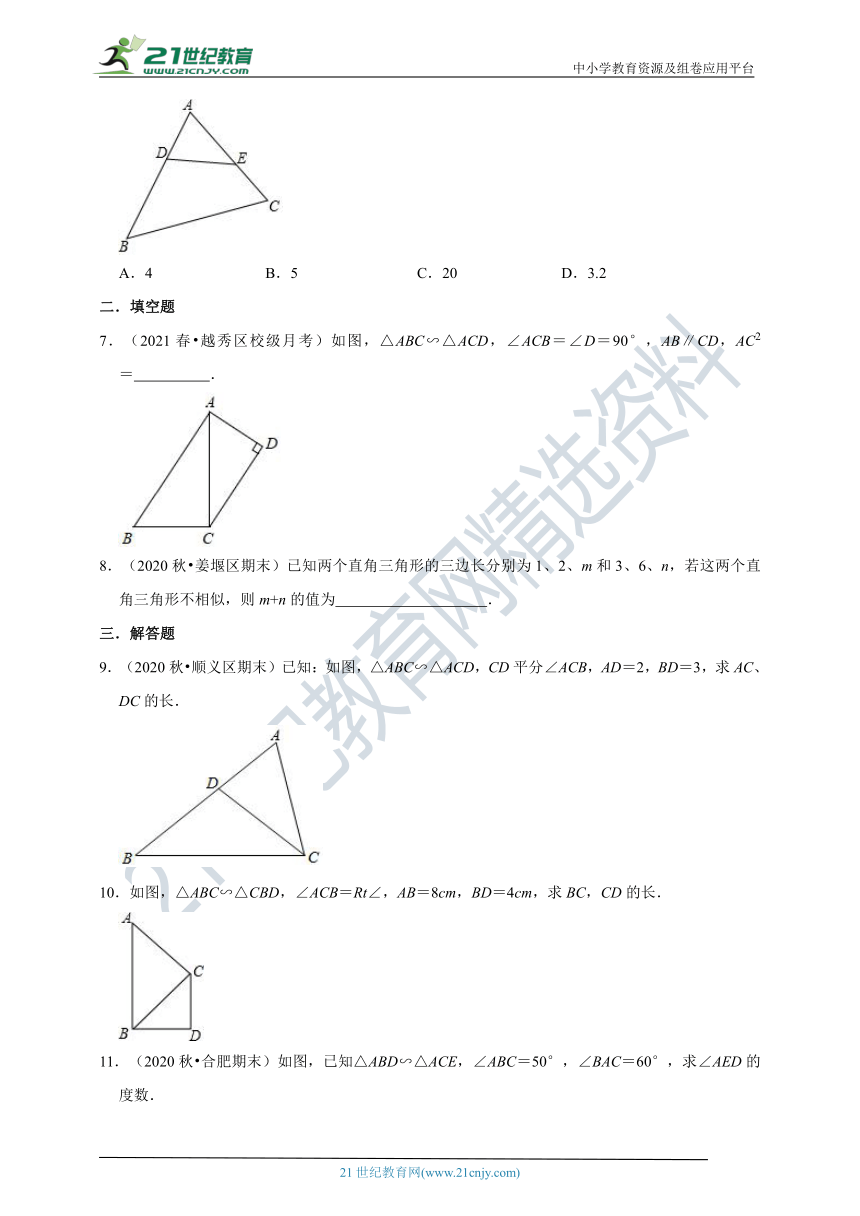
6.(2020秋?平果市期末)如图,已知△ADE∽△ACB,若AB=10,AC=8,AD=4,则AE的长是( )
A.4
B.5
C.20
D.3.2
二.填空题
7.(2021春?越秀区校级月考)如图,△ABC∽△ACD,∠ACB=∠D=90°,AB∥CD,AC2=
.
8.(2020秋?姜堰区期末)已知两个直角三角形的三边长分别为1、2、m和3、6、n,若这两个直角三角形不相似,则m+n的值为
.
三.解答题
9.(2020秋?顺义区期末)已知:如图,△ABC∽△ACD,CD平分∠ACB,AD=2,BD=3,求AC、DC的长.
10.如图,△ABC∽△CBD,∠ACB=Rt∠,AB=8cm,BD=4cm,求BC,CD的长.
11.(2020秋?合肥期末)如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数.
12.(2018秋?兴化市月考)如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
答案与解析
一.选择题
1.(2021?鄞州区模拟)如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2
B.
C.
D.4
【解答】解:∵△ABC∽△BDC,
∴=,
∵AC=4,CD=2,
∴BC2=AC?CD=4×2=8,
∴BC=2.
故选:B.
2.(2020秋?上虞区期末)如图,已知△ABC∽△A′B′C′,则图中角度α和边长x分别为( )
A.40°,9
B.40°,6
C.30°,9
D.30°,6
【解答】解:∵△ABC∽△A′B′C′,
∴∠α=40°,x=,
故选:A.
3.(2020秋?沂南县期末)如图,△ABC∽△DCA,∠B=33°,∠D=117°,则∠BAD的度数是( )
A.150°
B.147°
C.135°
D.120°
【解答】解:∵△ABC∽△DCA,
∴∠BAC=∠D=117°,∠DCA=∠B=33°,
∴∠DAC=180°﹣117°﹣33°=30°,
∴∠BAD=∠BAC+∠DAC=147°,
故选:B.
4.(2020秋?济南期末)如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
A.2
B.3
C.4
D.6
【解答】解:∵△ABO∽△CDO,
∴,
∵BO=8,DO=4,CD=3,
∴=,
解得:AB=6.
故选:D.
5.(2021?河池模拟)要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为4厘米,6厘米和9厘米,另一个三角形的最长边是18厘米,则它的最短边是( )
A.2厘米
B.4厘米
C.8厘米
D.12厘米
【解答】解:设另一个三角形的最短边长为xcm,
根据题意,得:=,
解得:x=8,
即另一个三角形的最短边的长为8cm.
故选:C.
6.(2020秋?平果市期末)如图,已知△ADE∽△ACB,若AB=10,AC=8,AD=4,则AE的长是( )
A.4
B.5
C.20
D.3.2
【解答】解:∵△ADE∽△ACB,
∴=,
∵AB=10,AC=8,AD=4,
∴=,
解得:AE=5.
故选:B.
二.填空题
7.(2021春?越秀区校级月考)如图,△ABC∽△ACD,∠ACB=∠D=90°,AB∥CD,AC2= AB?DC .
【解答】解:∵∠ACB=∠D=90°,且△ABC∽△ACD,
∴,
即AC2=AB?DC,
故答案为:AB?DC.
8.(2020秋?姜堰区期末)已知两个直角三角形的三边长分别为1、2、m和3、6、n,若这两个直角三角形不相似,则m+n的值为 .
【解答】解:当1,2为直角边,3,6也为直角边时,此时两三角形相似,不合题意;
当三边分别为1,2,,和3,6,3,此时两三角形相似,不合题意舍去;
当1,2为直角边,m=;则6为另一三角形的斜边,其直角边n为:,
故m+n=;
当3,6为直角边,n=;则2为另一三角形的斜边,其直角边m为:,
故m+n=.
故答案为:或.
三.解答题
9.(2020秋?顺义区期末)已知:如图,△ABC∽△ACD,CD平分∠ACB,AD=2,BD=3,求AC、DC的长.
【解答】解:∵△ABC∽△ACD,AD=2,BD=3,
∴∠ACD=∠B,=,即=,
解得,AC=,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠BCD=∠B,
∴DC=BD=3.
10.如图,△ABC∽△CBD,∠ACB=Rt∠,AB=8cm,BD=4cm,求BC,CD的长.
【解答】解:∵△ABC∽△CBD,AB=8cm,BD=4cm,
∴∠ACB=∠D=90°,=,即=,
解得:BC=﹣4(舍)或BC=4,
∵∠D=90°,
∴CD===4,
故BC=4cm,CD=4cm.
11.(2020秋?合肥期末)如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数.
【解答】解:∵∠ABC=50°,∠BAC=60°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=70°,
∵△ABD∽△ACE,
∴=,∠BAD=∠CAE,
∴=,∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAC=∠DAE,
∴△BAC∽△DAE,
∴∠AED=∠ACB,
∴∠AED=70°.
12.(2018秋?兴化市月考)如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
【解答】解:(1)∵∠BAC=75°,∠ABC=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=65°,
∵△ABC∽△ADE,
∴∠ADE=∠ABC=40°,∠AED=∠ACB=65°;
(2)∵△ABC∽△ADE,
∴=,
∵AB=30cm,BD=18cm,BC=20cm,
∴=,
∴DE=8(cm).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版九年级上
4.3相似三角形同步练习
一.选择题
1.(2021?鄞州区模拟)如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2
B.
C.
D.4
2.(2020秋?上虞区期末)如图,已知△ABC∽△A′B′C′,则图中角度α和边长x分别为( )
A.40°,9
B.40°,6
C.30°,9
D.30°,6
3.(2020秋?沂南县期末)如图,△ABC∽△DCA,∠B=33°,∠D=117°,则∠BAD的度数是( )
A.150°
B.147°
C.135°
D.120°
4.(2020秋?济南期末)如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
A.2
B.3
C.4
D.6
5.(2021?河池模拟)要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为4厘米,6厘米和9厘米,另一个三角形的最长边是18厘米,则它的最短边是( )
A.2厘米
B.4厘米
C.8厘米
D.12厘米
6.(2020秋?平果市期末)如图,已知△ADE∽△ACB,若AB=10,AC=8,AD=4,则AE的长是( )
A.4
B.5
C.20
D.3.2
二.填空题
7.(2021春?越秀区校级月考)如图,△ABC∽△ACD,∠ACB=∠D=90°,AB∥CD,AC2=
.
8.(2020秋?姜堰区期末)已知两个直角三角形的三边长分别为1、2、m和3、6、n,若这两个直角三角形不相似,则m+n的值为
.
三.解答题
9.(2020秋?顺义区期末)已知:如图,△ABC∽△ACD,CD平分∠ACB,AD=2,BD=3,求AC、DC的长.
10.如图,△ABC∽△CBD,∠ACB=Rt∠,AB=8cm,BD=4cm,求BC,CD的长.
11.(2020秋?合肥期末)如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数.
12.(2018秋?兴化市月考)如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
答案与解析
一.选择题
1.(2021?鄞州区模拟)如图,已知△ABC∽△BDC,其中AC=4,CD=2,则BC=( )
A.2
B.
C.
D.4
【解答】解:∵△ABC∽△BDC,
∴=,
∵AC=4,CD=2,
∴BC2=AC?CD=4×2=8,
∴BC=2.
故选:B.
2.(2020秋?上虞区期末)如图,已知△ABC∽△A′B′C′,则图中角度α和边长x分别为( )
A.40°,9
B.40°,6
C.30°,9
D.30°,6
【解答】解:∵△ABC∽△A′B′C′,
∴∠α=40°,x=,
故选:A.
3.(2020秋?沂南县期末)如图,△ABC∽△DCA,∠B=33°,∠D=117°,则∠BAD的度数是( )
A.150°
B.147°
C.135°
D.120°
【解答】解:∵△ABC∽△DCA,
∴∠BAC=∠D=117°,∠DCA=∠B=33°,
∴∠DAC=180°﹣117°﹣33°=30°,
∴∠BAD=∠BAC+∠DAC=147°,
故选:B.
4.(2020秋?济南期末)如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
A.2
B.3
C.4
D.6
【解答】解:∵△ABO∽△CDO,
∴,
∵BO=8,DO=4,CD=3,
∴=,
解得:AB=6.
故选:D.
5.(2021?河池模拟)要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为4厘米,6厘米和9厘米,另一个三角形的最长边是18厘米,则它的最短边是( )
A.2厘米
B.4厘米
C.8厘米
D.12厘米
【解答】解:设另一个三角形的最短边长为xcm,
根据题意,得:=,
解得:x=8,
即另一个三角形的最短边的长为8cm.
故选:C.
6.(2020秋?平果市期末)如图,已知△ADE∽△ACB,若AB=10,AC=8,AD=4,则AE的长是( )
A.4
B.5
C.20
D.3.2
【解答】解:∵△ADE∽△ACB,
∴=,
∵AB=10,AC=8,AD=4,
∴=,
解得:AE=5.
故选:B.
二.填空题
7.(2021春?越秀区校级月考)如图,△ABC∽△ACD,∠ACB=∠D=90°,AB∥CD,AC2= AB?DC .
【解答】解:∵∠ACB=∠D=90°,且△ABC∽△ACD,
∴,
即AC2=AB?DC,
故答案为:AB?DC.
8.(2020秋?姜堰区期末)已知两个直角三角形的三边长分别为1、2、m和3、6、n,若这两个直角三角形不相似,则m+n的值为 .
【解答】解:当1,2为直角边,3,6也为直角边时,此时两三角形相似,不合题意;
当三边分别为1,2,,和3,6,3,此时两三角形相似,不合题意舍去;
当1,2为直角边,m=;则6为另一三角形的斜边,其直角边n为:,
故m+n=;
当3,6为直角边,n=;则2为另一三角形的斜边,其直角边m为:,
故m+n=.
故答案为:或.
三.解答题
9.(2020秋?顺义区期末)已知:如图,△ABC∽△ACD,CD平分∠ACB,AD=2,BD=3,求AC、DC的长.
【解答】解:∵△ABC∽△ACD,AD=2,BD=3,
∴∠ACD=∠B,=,即=,
解得,AC=,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠BCD=∠B,
∴DC=BD=3.
10.如图,△ABC∽△CBD,∠ACB=Rt∠,AB=8cm,BD=4cm,求BC,CD的长.
【解答】解:∵△ABC∽△CBD,AB=8cm,BD=4cm,
∴∠ACB=∠D=90°,=,即=,
解得:BC=﹣4(舍)或BC=4,
∵∠D=90°,
∴CD===4,
故BC=4cm,CD=4cm.
11.(2020秋?合肥期末)如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数.
【解答】解:∵∠ABC=50°,∠BAC=60°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=70°,
∵△ABD∽△ACE,
∴=,∠BAD=∠CAE,
∴=,∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAC=∠DAE,
∴△BAC∽△DAE,
∴∠AED=∠ACB,
∴∠AED=70°.
12.(2018秋?兴化市月考)如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
【解答】解:(1)∵∠BAC=75°,∠ABC=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC=65°,
∵△ABC∽△ADE,
∴∠ADE=∠ABC=40°,∠AED=∠ACB=65°;
(2)∵△ABC∽△ADE,
∴=,
∵AB=30cm,BD=18cm,BC=20cm,
∴=,
∴DE=8(cm).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
