4.7 图形的位似同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级上
4.7图形的位似同步练习
一.选择题
1.(2021?重庆)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1
B.1:2
C.3:1
D.1:3
2.(2021?温州)如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8
B.9
C.10
D.15
3.(2021?南山区校级二模)已知△ABC与△A1B1C1是以原点为中心的位似图形,且A(3,1),△ABC与△A1B1C1的相似比为,则A的对应点A1的坐标是( )
A.(6,2)
B.(﹣6,﹣2)
C.(6,2)或(﹣6,﹣2)
D.(2,6)
4.(2021?重庆模拟)如图,在△ABC外任取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,顺次连接DE、EF、DF得到△DEF,则下列说法错误的是( )
A.△DEF与△ABC是位似图形
B.△DEF与△ABC是相似图形
C.△DEF与△ABC的周长比是1:2
D.△DEF与△ABC的面积比是1:2
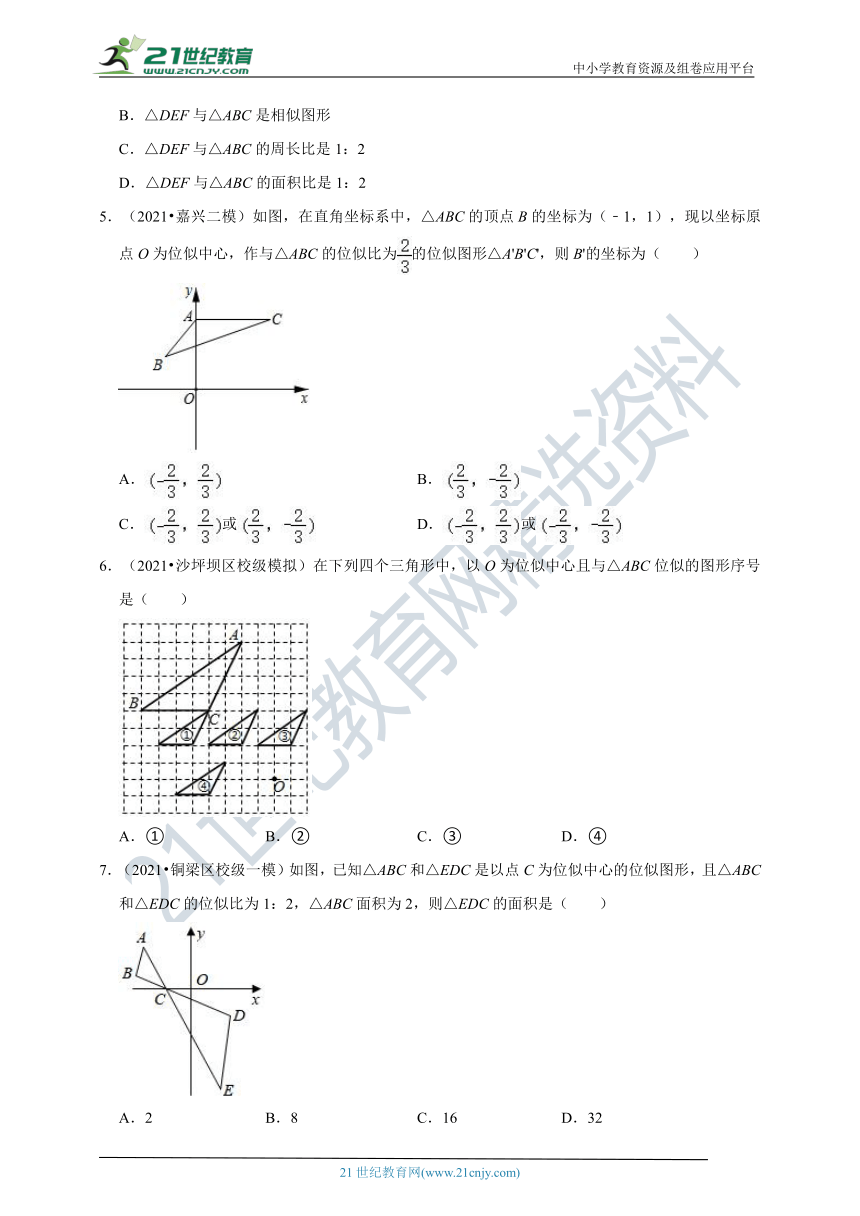
5.(2021?嘉兴二模)如图,在直角坐标系中,△ABC的顶点B的坐标为(﹣1,1),现以坐标原点O为位似中心,作与△ABC的位似比为的位似图形△A'B'C',则B'的坐标为( )
A.
B.
C.或
D.或
6.(2021?沙坪坝区校级模拟)在下列四个三角形中,以O为位似中心且与△ABC位似的图形序号是( )
A.①
B.②
C.③
D.④
7.(2021?铜梁区校级一模)如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为2,则△EDC的面积是( )
A.2
B.8
C.16
D.32
8.(2021?重庆)如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )
A.1:2
B.1:4
C.1:3
D.1:9
二.填空题
9.(2021?越秀区校级二模)在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,作与△OAB的位似比为的位似图形△OCD,则点C坐标为
.
10.(2021?嘉兴)如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是
.
11.(2021?滨城区二模)在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,已知A(2,3),则点A1的坐标是
.
12.(2020秋?汉寿县期末)如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(1,2),点E的坐标为,则点P的坐标为
.
13.(2020秋?成都期末)在平面直角坐标中,△ABC的顶点坐标分别是A(1,1),B(4,2),C(3,5),以点A为位似中心,相似比为1:2.把三角形ABC缩小,得到△AB1C1,则点C的对应点C1的坐标为
.
14.(2020秋?定远县月考)在如图所示的网格中,以点O为位似中心,作四边形ABCD的位似图形,小明认为四边形ABCD的位似图形是四边形NHMR;小亮认为四边形ABCD的位似图形是四边形NPMQ.你认为正确的是
.(选填“小明”或“小亮”)
15.(2021?万州区模拟)如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为4,则△EDC的面积是
.
三.解答题
16.(2021?包河区三模)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,5).
(1)请画出△ABC关于x轴的对称图形△A1B1C1;
(2)以0为位似中心,在第三象限内画出△ABC的位似图形△A2B2C2,且位似比为1;
(3)借助网格,利用无刻度直尺画出线段CD,使CD平分△ABC的面积.(保留确定点D的痕迹)
17.(2021?霍邱县一模)如图,每一个小方格正方形的边长均为一个单位长度,△ABC的顶点的坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)请在网格中画出△ABC关于原点O的中心对称图形△A1B1C1.
(2)以点O为位似中心,位似比为2:1,将△ABC放大得到△A2B2C2,请在网格中画出△A2B2C2(不要超出方格区域).
(3)求△A2B2C2的面积.
18.(2021春?南岗区校级月考)如图是按照一定比例缩放的两个图形.
(1)请你画出图②按4:1的比放大后的图形③.
(2)图③也可以看成是由图①按
:
放大后得到的.
19.(2021春?东城区校级月考)如图,在平面直角坐标系中,△QAB的顶点坐标分别为O(0,0),A(2,1),B(1,﹣2).
(1)以原点O为位似中心,在y轴的右侧画出将△OAB放大为原来的2倍得到的△OA1B1,请写出点A的对应点A1的坐标;
(2)将△OAB以原点为旋转中心,顺时针旋转90度后得到△O2A2B2,求线段OB在旋转过程中扫过的面积.
20.(2020秋?禹城市期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于原点O成中心对称,写出△A1B1C1的各顶点的坐标;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标;
(3)若△ABC和△A2B2C2关于点(﹣1,1)位似,位似比为1:2,画出△A2B2C2(在位似中心另一侧)并写出△A2B2C2各顶点的坐标.
答案与解析
一.选择题
1.(2021?重庆)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1
B.1:2
C.3:1
D.1:3
【解析】解:∵B(0,1),D(0,3),
∴OB=1,OD=3,
∵△OAB以原点O为位似中心放大后得到△OCD,
∴△OAB与△OCD的相似比是OB:OD=1:3,
故选:D.
2.(2021?温州)如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8
B.9
C.10
D.15
【解析】解:∵图形甲与图形乙是位似图形,位似比为2:3,AB=6,
∴=,即=,
解得,A′B′=9,
故选:B.
3.(2021?南山区校级二模)已知△ABC与△A1B1C1是以原点为中心的位似图形,且A(3,1),△ABC与△A1B1C1的相似比为,则A的对应点A1的坐标是( )
A.(6,2)
B.(﹣6,﹣2)
C.(6,2)或(﹣6,﹣2)
D.(2,6)
【解析】解:∵△ABC与△A1B1C1是以原点为中心的位似图形,A(3,1),△ABC与△A1B1C1的相似比为,
∴点A的对应点A1的坐标为(3×2,1×2)或(3×(﹣2),1×(﹣2)),即(6,2)或(﹣6,﹣2),
故选:C.
4.(2021?重庆模拟)如图,在△ABC外任取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,顺次连接DE、EF、DF得到△DEF,则下列说法错误的是( )
A.△DEF与△ABC是位似图形
B.△DEF与△ABC是相似图形
C.△DEF与△ABC的周长比是1:2
D.△DEF与△ABC的面积比是1:2
【解析】解:∵AO、BO、CO的中点分别为D、E、F,
∴EF∥BC,EF=BC,DF∥AC,DF=AC,DE∥AB,DE=AB,
∴△ADEF∽△ABC,
∴△DEF与△ABC是位似图形,位似中心为点O,
∴△DEF与△ABC是相似图形,
∴△DEF与△ABC的周长比是1:2,△DEF与△ABC的面积比是1:4,
∴D选项说法错误,
故选:D.
5.(2021?嘉兴二模)如图,在直角坐标系中,△ABC的顶点B的坐标为(﹣1,1),现以坐标原点O为位似中心,作与△ABC的位似比为的位似图形△A'B'C',则B'的坐标为( )
A.
B.
C.或
D.或
【解析】解:∵位似中心为坐标原点,作与△ABC的位似比为的位似图形△A'B'C',
而B的坐标为(﹣1,1),
∴B'的坐标为(﹣,)或(,﹣).
故选:C.
6.(2021?沙坪坝区校级模拟)在下列四个三角形中,以O为位似中心且与△ABC位似的图形序号是( )
A.①
B.②
C.③
D.④
【解析】解:连接OA、OB、OC,
∵图②的三个顶点分别在OA、OB、OC上,
∴以O为位似中心且与△ABC位似的图形序号是②,
故选:B.
7.(2021?铜梁区校级一模)如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为2,则△EDC的面积是( )
A.2
B.8
C.16
D.32
【解析】解:∵△ABC和△EDC是以点C为位似中心的位似图形,
∴△ABC∽△EDC,
∵△ABC和△EDC的位似比为1:2,
∴△ABC和△EDC的相似比为1:2,
∴△ABC和△EDC的面积比为1:4,
∵△ABC面积为2,
∴△EDC的面积是2×4=8,
故选:B.
8.(2021?重庆)如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )
A.1:2
B.1:4
C.1:3
D.1:9
【解析】解:∵△ABC与△DEF位似,
∴△ABC∽△DEF,BC∥EF,
∴△OBC∽△OEF,
∴==,即△ABC与△DEF的相似比为1:2,
∴△ABC与△DEF的周长之比为1:2,
故选:A.
二.填空题
9.(2021?越秀区校级二模)在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,作与△OAB的位似比为的位似图形△OCD,则点C坐标为
(,1)或(﹣,﹣1) .
【解析】解:∵以点O为位似中心,作与△OAB的位似比为的位似图形△OCD,
而A(4,3),
∴C(×4,×3)或(﹣×4,﹣×3),
即C(,1)或(﹣,﹣1).
故答案为C(,1)或(﹣,﹣1).
10.(2021?嘉兴)如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是
(4,2) .
【解析】解:如图,
点G(4,2)即为所求的位似中心.
故答案是:(4,2).
11.(2021?滨城区二模)在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,已知A(2,3),则点A1的坐标是 (,2)或(﹣,﹣2) .
【解析】解:∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,点A的坐标为(2,3),
∴点A1的坐标为(2×,3×)或(2×(﹣),3×(﹣)),
即(,2)或(﹣,﹣2),
故答案为:(,2)或(﹣,﹣2).
12.(2020秋?汉寿县期末)如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(1,2),点E的坐标为,则点P的坐标为 (﹣1,0) .
【解析】解:∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点B的坐标为(1,2),点E的坐标为,
∴EF=1,CO=2,FO=,
∵EF∥CO,
∴△PEF∽△PCO,
∴=,
则=,
解得:PF=,
故PO=+=1,
则点P的坐标为(﹣1,0).
故答案为:(﹣1,0).
13.(2020秋?成都期末)在平面直角坐标中,△ABC的顶点坐标分别是A(1,1),B(4,2),C(3,5),以点A为位似中心,相似比为1:2.把三角形ABC缩小,得到△AB1C1,则点C的对应点C1的坐标为 (2,3)或(0,﹣1) .
【解析】解:以点A为坐标原点建立新的平面直角坐标系,
则在新坐标系中,点C的坐标为(2,4),
以以点A为位似中心,相似比为1:2.把三角形ABC缩小,得到△AB1C1,
则点C的对应点C1在新坐标系中的坐标为(2×,4×)或(﹣2×,﹣4×),即(1,2)或(﹣1,﹣2),
在原坐标系中,点C1的坐标为(2,3)或(0,﹣1),
故答案为:(2,3)或(0,﹣1).
14.(2020秋?定远县月考)在如图所示的网格中,以点O为位似中心,作四边形ABCD的位似图形,小明认为四边形ABCD的位似图形是四边形NHMR;小亮认为四边形ABCD的位似图形是四边形NPMQ.你认为正确的是 小亮 .(选填“小明”或“小亮”)
【解析】解:如图,
四边形ABCD的位似图形是四边形NPMQ.
故答案为小亮.
15.(2021?万州区模拟)如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为4,则△EDC的面积是 16 .
【解析】解:∵△ABC和△EDC是以点C为位似中心的位似图形,
∴△ABC∽△EDC,
∵△ABC和△EDC的位似比为1:2,
∴△ABC和△EDC的相似比为1:2,
∴△ABC和△EDC的面积比为1:4,
∵△ABC面积为4,
∴△EDC的面积是:4×22=4×4=16,
故答案为:16.
三.解答题
16.(2021?包河区三模)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,5).
(1)请画出△ABC关于x轴的对称图形△A1B1C1;
(2)以0为位似中心,在第三象限内画出△ABC的位似图形△A2B2C2,且位似比为1;
(3)借助网格,利用无刻度直尺画出线段CD,使CD平分△ABC的面积.(保留确定点D的痕迹)
【解析】解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2即为所求;
(3)如图所示:CD即为所求.
17.(2021?霍邱县一模)如图,每一个小方格正方形的边长均为一个单位长度,△ABC的顶点的坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)请在网格中画出△ABC关于原点O的中心对称图形△A1B1C1.
(2)以点O为位似中心,位似比为2:1,将△ABC放大得到△A2B2C2,请在网格中画出△A2B2C2(不要超出方格区域).
(3)求△A2B2C2的面积.
【解析】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)△A2B2C2的面积=4S△ABC=4(4×3﹣×4×1﹣×3×1﹣×3×2)=22.
18.(2021春?南岗区校级月考)如图是按照一定比例缩放的两个图形.
(1)请你画出图②按4:1的比放大后的图形③.
(2)图③也可以看成是由图①按 3 : 4 放大后得到的.
【解析】解:(1)如图,图③为所作;
(2)图③也可以看成是由图①按3:4放大后得到的.
故答案为3,4.
19.(2021春?东城区校级月考)如图,在平面直角坐标系中,△QAB的顶点坐标分别为O(0,0),A(2,1),B(1,﹣2).
(1)以原点O为位似中心,在y轴的右侧画出将△OAB放大为原来的2倍得到的△OA1B1,请写出点A的对应点A1的坐标;
(2)将△OAB以原点为旋转中心,顺时针旋转90度后得到△O2A2B2,求线段OB在旋转过程中扫过的面积.
【解析】解:(1)如图,△OA1B1即为所求作,A1(4,2).
(2)如图,△O2A2B2,即为所求作.
线段OB在旋转过程中扫过的面积==π.
20.(2020秋?禹城市期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于原点O成中心对称,写出△A1B1C1的各顶点的坐标;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标;
(3)若△ABC和△A2B2C2关于点(﹣1,1)位似,位似比为1:2,画出△A2B2C2(在位似中心另一侧)并写出△A2B2C2各顶点的坐标.
【解析】解:(1)如图所示,△A1B1C1即为所求,
由图知A1(3,﹣5),B1(2,﹣1),C1(1,﹣3).
(2)如图,△PAB即为所求,
点A关于x轴的对称点A′的坐标为(﹣3,﹣5),
设BA′的解析式为y=kx+b,
把A′(﹣3,﹣5),B(﹣2,1)代入得,解得
∴BA′的解析式为y=6x+13,
当y=0时,6x+13=0,解得x=﹣,
∴点P(﹣,0);
(3)如图所示,△A2B2C2即为所求,A2(3,﹣7),B2(1,1),C2(﹣1,﹣3).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版九年级上
4.7图形的位似同步练习
一.选择题
1.(2021?重庆)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1
B.1:2
C.3:1
D.1:3
2.(2021?温州)如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8
B.9
C.10
D.15
3.(2021?南山区校级二模)已知△ABC与△A1B1C1是以原点为中心的位似图形,且A(3,1),△ABC与△A1B1C1的相似比为,则A的对应点A1的坐标是( )
A.(6,2)
B.(﹣6,﹣2)
C.(6,2)或(﹣6,﹣2)
D.(2,6)
4.(2021?重庆模拟)如图,在△ABC外任取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,顺次连接DE、EF、DF得到△DEF,则下列说法错误的是( )
A.△DEF与△ABC是位似图形
B.△DEF与△ABC是相似图形
C.△DEF与△ABC的周长比是1:2
D.△DEF与△ABC的面积比是1:2
5.(2021?嘉兴二模)如图,在直角坐标系中,△ABC的顶点B的坐标为(﹣1,1),现以坐标原点O为位似中心,作与△ABC的位似比为的位似图形△A'B'C',则B'的坐标为( )
A.
B.
C.或
D.或
6.(2021?沙坪坝区校级模拟)在下列四个三角形中,以O为位似中心且与△ABC位似的图形序号是( )
A.①
B.②
C.③
D.④
7.(2021?铜梁区校级一模)如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为2,则△EDC的面积是( )
A.2
B.8
C.16
D.32
8.(2021?重庆)如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )
A.1:2
B.1:4
C.1:3
D.1:9
二.填空题
9.(2021?越秀区校级二模)在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,作与△OAB的位似比为的位似图形△OCD,则点C坐标为
.
10.(2021?嘉兴)如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是
.
11.(2021?滨城区二模)在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,已知A(2,3),则点A1的坐标是
.
12.(2020秋?汉寿县期末)如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(1,2),点E的坐标为,则点P的坐标为
.
13.(2020秋?成都期末)在平面直角坐标中,△ABC的顶点坐标分别是A(1,1),B(4,2),C(3,5),以点A为位似中心,相似比为1:2.把三角形ABC缩小,得到△AB1C1,则点C的对应点C1的坐标为
.
14.(2020秋?定远县月考)在如图所示的网格中,以点O为位似中心,作四边形ABCD的位似图形,小明认为四边形ABCD的位似图形是四边形NHMR;小亮认为四边形ABCD的位似图形是四边形NPMQ.你认为正确的是
.(选填“小明”或“小亮”)
15.(2021?万州区模拟)如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为4,则△EDC的面积是
.
三.解答题
16.(2021?包河区三模)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,5).
(1)请画出△ABC关于x轴的对称图形△A1B1C1;
(2)以0为位似中心,在第三象限内画出△ABC的位似图形△A2B2C2,且位似比为1;
(3)借助网格,利用无刻度直尺画出线段CD,使CD平分△ABC的面积.(保留确定点D的痕迹)
17.(2021?霍邱县一模)如图,每一个小方格正方形的边长均为一个单位长度,△ABC的顶点的坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)请在网格中画出△ABC关于原点O的中心对称图形△A1B1C1.
(2)以点O为位似中心,位似比为2:1,将△ABC放大得到△A2B2C2,请在网格中画出△A2B2C2(不要超出方格区域).
(3)求△A2B2C2的面积.
18.(2021春?南岗区校级月考)如图是按照一定比例缩放的两个图形.
(1)请你画出图②按4:1的比放大后的图形③.
(2)图③也可以看成是由图①按
:
放大后得到的.
19.(2021春?东城区校级月考)如图,在平面直角坐标系中,△QAB的顶点坐标分别为O(0,0),A(2,1),B(1,﹣2).
(1)以原点O为位似中心,在y轴的右侧画出将△OAB放大为原来的2倍得到的△OA1B1,请写出点A的对应点A1的坐标;
(2)将△OAB以原点为旋转中心,顺时针旋转90度后得到△O2A2B2,求线段OB在旋转过程中扫过的面积.
20.(2020秋?禹城市期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于原点O成中心对称,写出△A1B1C1的各顶点的坐标;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标;
(3)若△ABC和△A2B2C2关于点(﹣1,1)位似,位似比为1:2,画出△A2B2C2(在位似中心另一侧)并写出△A2B2C2各顶点的坐标.
答案与解析
一.选择题
1.(2021?重庆)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1
B.1:2
C.3:1
D.1:3
【解析】解:∵B(0,1),D(0,3),
∴OB=1,OD=3,
∵△OAB以原点O为位似中心放大后得到△OCD,
∴△OAB与△OCD的相似比是OB:OD=1:3,
故选:D.
2.(2021?温州)如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为( )
A.8
B.9
C.10
D.15
【解析】解:∵图形甲与图形乙是位似图形,位似比为2:3,AB=6,
∴=,即=,
解得,A′B′=9,
故选:B.
3.(2021?南山区校级二模)已知△ABC与△A1B1C1是以原点为中心的位似图形,且A(3,1),△ABC与△A1B1C1的相似比为,则A的对应点A1的坐标是( )
A.(6,2)
B.(﹣6,﹣2)
C.(6,2)或(﹣6,﹣2)
D.(2,6)
【解析】解:∵△ABC与△A1B1C1是以原点为中心的位似图形,A(3,1),△ABC与△A1B1C1的相似比为,
∴点A的对应点A1的坐标为(3×2,1×2)或(3×(﹣2),1×(﹣2)),即(6,2)或(﹣6,﹣2),
故选:C.
4.(2021?重庆模拟)如图,在△ABC外任取一点O,连接AO、BO、CO,并分别取它们的中点D、E、F,顺次连接DE、EF、DF得到△DEF,则下列说法错误的是( )
A.△DEF与△ABC是位似图形
B.△DEF与△ABC是相似图形
C.△DEF与△ABC的周长比是1:2
D.△DEF与△ABC的面积比是1:2
【解析】解:∵AO、BO、CO的中点分别为D、E、F,
∴EF∥BC,EF=BC,DF∥AC,DF=AC,DE∥AB,DE=AB,
∴△ADEF∽△ABC,
∴△DEF与△ABC是位似图形,位似中心为点O,
∴△DEF与△ABC是相似图形,
∴△DEF与△ABC的周长比是1:2,△DEF与△ABC的面积比是1:4,
∴D选项说法错误,
故选:D.
5.(2021?嘉兴二模)如图,在直角坐标系中,△ABC的顶点B的坐标为(﹣1,1),现以坐标原点O为位似中心,作与△ABC的位似比为的位似图形△A'B'C',则B'的坐标为( )
A.
B.
C.或
D.或
【解析】解:∵位似中心为坐标原点,作与△ABC的位似比为的位似图形△A'B'C',
而B的坐标为(﹣1,1),
∴B'的坐标为(﹣,)或(,﹣).
故选:C.
6.(2021?沙坪坝区校级模拟)在下列四个三角形中,以O为位似中心且与△ABC位似的图形序号是( )
A.①
B.②
C.③
D.④
【解析】解:连接OA、OB、OC,
∵图②的三个顶点分别在OA、OB、OC上,
∴以O为位似中心且与△ABC位似的图形序号是②,
故选:B.
7.(2021?铜梁区校级一模)如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为2,则△EDC的面积是( )
A.2
B.8
C.16
D.32
【解析】解:∵△ABC和△EDC是以点C为位似中心的位似图形,
∴△ABC∽△EDC,
∵△ABC和△EDC的位似比为1:2,
∴△ABC和△EDC的相似比为1:2,
∴△ABC和△EDC的面积比为1:4,
∵△ABC面积为2,
∴△EDC的面积是2×4=8,
故选:B.
8.(2021?重庆)如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )
A.1:2
B.1:4
C.1:3
D.1:9
【解析】解:∵△ABC与△DEF位似,
∴△ABC∽△DEF,BC∥EF,
∴△OBC∽△OEF,
∴==,即△ABC与△DEF的相似比为1:2,
∴△ABC与△DEF的周长之比为1:2,
故选:A.
二.填空题
9.(2021?越秀区校级二模)在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,作与△OAB的位似比为的位似图形△OCD,则点C坐标为
(,1)或(﹣,﹣1) .
【解析】解:∵以点O为位似中心,作与△OAB的位似比为的位似图形△OCD,
而A(4,3),
∴C(×4,×3)或(﹣×4,﹣×3),
即C(,1)或(﹣,﹣1).
故答案为C(,1)或(﹣,﹣1).
10.(2021?嘉兴)如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是
(4,2) .
【解析】解:如图,
点G(4,2)即为所求的位似中心.
故答案是:(4,2).
11.(2021?滨城区二模)在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,已知A(2,3),则点A1的坐标是 (,2)或(﹣,﹣2) .
【解析】解:∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,点A的坐标为(2,3),
∴点A1的坐标为(2×,3×)或(2×(﹣),3×(﹣)),
即(,2)或(﹣,﹣2),
故答案为:(,2)或(﹣,﹣2).
12.(2020秋?汉寿县期末)如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(1,2),点E的坐标为,则点P的坐标为 (﹣1,0) .
【解析】解:∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点B的坐标为(1,2),点E的坐标为,
∴EF=1,CO=2,FO=,
∵EF∥CO,
∴△PEF∽△PCO,
∴=,
则=,
解得:PF=,
故PO=+=1,
则点P的坐标为(﹣1,0).
故答案为:(﹣1,0).
13.(2020秋?成都期末)在平面直角坐标中,△ABC的顶点坐标分别是A(1,1),B(4,2),C(3,5),以点A为位似中心,相似比为1:2.把三角形ABC缩小,得到△AB1C1,则点C的对应点C1的坐标为 (2,3)或(0,﹣1) .
【解析】解:以点A为坐标原点建立新的平面直角坐标系,
则在新坐标系中,点C的坐标为(2,4),
以以点A为位似中心,相似比为1:2.把三角形ABC缩小,得到△AB1C1,
则点C的对应点C1在新坐标系中的坐标为(2×,4×)或(﹣2×,﹣4×),即(1,2)或(﹣1,﹣2),
在原坐标系中,点C1的坐标为(2,3)或(0,﹣1),
故答案为:(2,3)或(0,﹣1).
14.(2020秋?定远县月考)在如图所示的网格中,以点O为位似中心,作四边形ABCD的位似图形,小明认为四边形ABCD的位似图形是四边形NHMR;小亮认为四边形ABCD的位似图形是四边形NPMQ.你认为正确的是 小亮 .(选填“小明”或“小亮”)
【解析】解:如图,
四边形ABCD的位似图形是四边形NPMQ.
故答案为小亮.
15.(2021?万州区模拟)如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为4,则△EDC的面积是 16 .
【解析】解:∵△ABC和△EDC是以点C为位似中心的位似图形,
∴△ABC∽△EDC,
∵△ABC和△EDC的位似比为1:2,
∴△ABC和△EDC的相似比为1:2,
∴△ABC和△EDC的面积比为1:4,
∵△ABC面积为4,
∴△EDC的面积是:4×22=4×4=16,
故答案为:16.
三.解答题
16.(2021?包河区三模)如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,5).
(1)请画出△ABC关于x轴的对称图形△A1B1C1;
(2)以0为位似中心,在第三象限内画出△ABC的位似图形△A2B2C2,且位似比为1;
(3)借助网格,利用无刻度直尺画出线段CD,使CD平分△ABC的面积.(保留确定点D的痕迹)
【解析】解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2即为所求;
(3)如图所示:CD即为所求.
17.(2021?霍邱县一模)如图,每一个小方格正方形的边长均为一个单位长度,△ABC的顶点的坐标分别为A(﹣2,﹣2),B(﹣5,﹣4),C(﹣1,﹣5).
(1)请在网格中画出△ABC关于原点O的中心对称图形△A1B1C1.
(2)以点O为位似中心,位似比为2:1,将△ABC放大得到△A2B2C2,请在网格中画出△A2B2C2(不要超出方格区域).
(3)求△A2B2C2的面积.
【解析】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)△A2B2C2的面积=4S△ABC=4(4×3﹣×4×1﹣×3×1﹣×3×2)=22.
18.(2021春?南岗区校级月考)如图是按照一定比例缩放的两个图形.
(1)请你画出图②按4:1的比放大后的图形③.
(2)图③也可以看成是由图①按 3 : 4 放大后得到的.
【解析】解:(1)如图,图③为所作;
(2)图③也可以看成是由图①按3:4放大后得到的.
故答案为3,4.
19.(2021春?东城区校级月考)如图,在平面直角坐标系中,△QAB的顶点坐标分别为O(0,0),A(2,1),B(1,﹣2).
(1)以原点O为位似中心,在y轴的右侧画出将△OAB放大为原来的2倍得到的△OA1B1,请写出点A的对应点A1的坐标;
(2)将△OAB以原点为旋转中心,顺时针旋转90度后得到△O2A2B2,求线段OB在旋转过程中扫过的面积.
【解析】解:(1)如图,△OA1B1即为所求作,A1(4,2).
(2)如图,△O2A2B2,即为所求作.
线段OB在旋转过程中扫过的面积==π.
20.(2020秋?禹城市期末)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于原点O成中心对称,写出△A1B1C1的各顶点的坐标;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标;
(3)若△ABC和△A2B2C2关于点(﹣1,1)位似,位似比为1:2,画出△A2B2C2(在位似中心另一侧)并写出△A2B2C2各顶点的坐标.
【解析】解:(1)如图所示,△A1B1C1即为所求,
由图知A1(3,﹣5),B1(2,﹣1),C1(1,﹣3).
(2)如图,△PAB即为所求,
点A关于x轴的对称点A′的坐标为(﹣3,﹣5),
设BA′的解析式为y=kx+b,
把A′(﹣3,﹣5),B(﹣2,1)代入得,解得
∴BA′的解析式为y=6x+13,
当y=0时,6x+13=0,解得x=﹣,
∴点P(﹣,0);
(3)如图所示,△A2B2C2即为所求,A2(3,﹣7),B2(1,1),C2(﹣1,﹣3).
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
