浙教版数学七年级上册:1.4有理数大小的比较同步新授课件(18张PPT)
文档属性
| 名称 | 浙教版数学七年级上册:1.4有理数大小的比较同步新授课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第一章
有理数
1.4
有理数大小的比较
知识回顾
什么叫做绝对值?
数轴上表示一个数的点与原点的距离,就是这个数的绝对值.
获取新知
哈尔滨-20℃
北京-10℃
广州10℃
武汉5℃
上海0℃
比较这一天下列各个城市间最低气温的高低(填“高于”或“低于”)
广州_______上海;
北京________上海;北京________哈尔
滨;武汉________哈尔滨;武汉__________广州.
高于
低于
低于
高于
高于
把表示上述五个城市这一天最低气温的数表示在数轴上.观
察这五个数在数轴上的位置,你发现什么?
0
5
10
-10
-20
-15
-5
五个城市温度的高低如下:
哈尔滨
北京
上海
武汉
广州
-20℃
<
-10
℃
<
0
℃
<
5
℃
<
10
℃
0
5
10
-10
-20
-15
-5
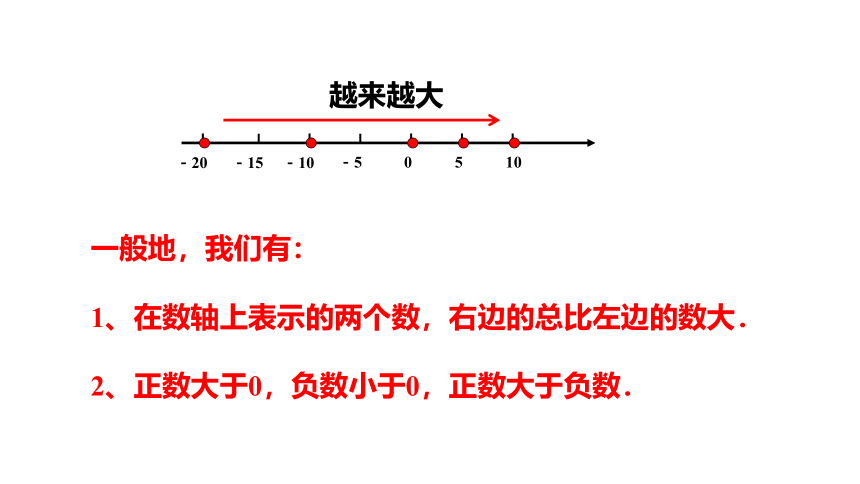
越来越大
一般地,我们有:
1、在数轴上表示的两个数,右边的总比左边的数大.
2、正数大于0,负数小于0,正数大于负数.
例题精讲
例1
在数轴上表示数5,0,-4,-1,并比较它们的大小,将
它们按从小到大的顺序用“<”连接起来.
解:
5,0,-4,-1
在数轴上表示如图
:
–1
–2
–3
–4
1
2
3
4
5
0
将它们按从小到大的顺序排列为-4<-1
<
0
<
5.
两个正数比较大小,绝对值大的数大;两个负数比较
大小,绝对值大的数反而小.
例2
比较下列各对数的大小,并说明理由:
(1)1与-10;
(2)-0.001与0
;
(3)
与
.
解:(1)
1>-10,
(正数大于一切负数)
(2)-0.001<0,
(负数都小于零)
(3)∵
∴
(两个负数比较大小,绝对值大的数反而小).
∴
课堂小结
正数都______0,负数都______0,正数______负数.
大于
小于
大于
大
小
大于
正数
小于
有理数的大小比较
借助法则
两个正数比较大小,绝对值大的数________
两个负数比较大小,绝对值大的数反而________
一正一负,正数________负数
其中一个数为零,________大于零,负数________零
大
小
大于
随堂演练
1.
如图1-4-1,数轴上有A,B,C,D四个点,其中所对应的数最小的点是( )
A.点A
B.点B
C.点C
D.点D
A
2.有理数a,b,c在数轴上所对应的点的位置如图,则下列关系正确的是( )
A.c>a>0>b
B.a>b>0>c
C.b>0>a>c
D.b>0>c>a
C
3.
比较下列各组数的大小:
(1)1与-100;
解:(1)1>-100.
解:
(2)∵
=-0.625,0.625>0.618,
∴-0.625<-0.618,即
<-0.618.
5
-
—
8
5
-
—
8
(2)
与-0.618.
4.有关数轴上的数,下面说法正确的是
( )
A.两个有理数,绝对值大的离原点远
B.两个有理数,绝对值大的在右边
C.两个负有理数,绝对值大的离原点近
D.两个有理数,绝对值大的离原点近
A
5.[2019·桐乡城区联考]
大于-5的负整数的个数是
( )
A.3
B.4
C.5
D.6
B
6.已知a,b是有理数,它们在数轴上的对应点的位置如图所示,则a,b,-a,-b这四个数中最小的是( )
A.a
B.b
C.-a
D.-b
B
7、比较a与-a
的大小.
解:
当a>0时,a>-a
;
当a=0时,a=-a
;
当a<0时,a<-a
.
第一章
有理数
1.4
有理数大小的比较
知识回顾
什么叫做绝对值?
数轴上表示一个数的点与原点的距离,就是这个数的绝对值.
获取新知
哈尔滨-20℃
北京-10℃
广州10℃
武汉5℃
上海0℃
比较这一天下列各个城市间最低气温的高低(填“高于”或“低于”)
广州_______上海;
北京________上海;北京________哈尔
滨;武汉________哈尔滨;武汉__________广州.
高于
低于
低于
高于
高于
把表示上述五个城市这一天最低气温的数表示在数轴上.观
察这五个数在数轴上的位置,你发现什么?
0
5
10
-10
-20
-15
-5
五个城市温度的高低如下:
哈尔滨
北京
上海
武汉
广州
-20℃
<
-10
℃
<
0
℃
<
5
℃
<
10
℃
0
5
10
-10
-20
-15
-5
越来越大
一般地,我们有:
1、在数轴上表示的两个数,右边的总比左边的数大.
2、正数大于0,负数小于0,正数大于负数.
例题精讲
例1
在数轴上表示数5,0,-4,-1,并比较它们的大小,将
它们按从小到大的顺序用“<”连接起来.
解:
5,0,-4,-1
在数轴上表示如图
:
–1
–2
–3
–4
1
2
3
4
5
0
将它们按从小到大的顺序排列为-4<-1
<
0
<
5.
两个正数比较大小,绝对值大的数大;两个负数比较
大小,绝对值大的数反而小.
例2
比较下列各对数的大小,并说明理由:
(1)1与-10;
(2)-0.001与0
;
(3)
与
.
解:(1)
1>-10,
(正数大于一切负数)
(2)-0.001<0,
(负数都小于零)
(3)∵
∴
(两个负数比较大小,绝对值大的数反而小).
∴
课堂小结
正数都______0,负数都______0,正数______负数.
大于
小于
大于
大
小
大于
正数
小于
有理数的大小比较
借助法则
两个正数比较大小,绝对值大的数________
两个负数比较大小,绝对值大的数反而________
一正一负,正数________负数
其中一个数为零,________大于零,负数________零
大
小
大于
随堂演练
1.
如图1-4-1,数轴上有A,B,C,D四个点,其中所对应的数最小的点是( )
A.点A
B.点B
C.点C
D.点D
A
2.有理数a,b,c在数轴上所对应的点的位置如图,则下列关系正确的是( )
A.c>a>0>b
B.a>b>0>c
C.b>0>a>c
D.b>0>c>a
C
3.
比较下列各组数的大小:
(1)1与-100;
解:(1)1>-100.
解:
(2)∵
=-0.625,0.625>0.618,
∴-0.625<-0.618,即
<-0.618.
5
-
—
8
5
-
—
8
(2)
与-0.618.
4.有关数轴上的数,下面说法正确的是
( )
A.两个有理数,绝对值大的离原点远
B.两个有理数,绝对值大的在右边
C.两个负有理数,绝对值大的离原点近
D.两个有理数,绝对值大的离原点近
A
5.[2019·桐乡城区联考]
大于-5的负整数的个数是
( )
A.3
B.4
C.5
D.6
B
6.已知a,b是有理数,它们在数轴上的对应点的位置如图所示,则a,b,-a,-b这四个数中最小的是( )
A.a
B.b
C.-a
D.-b
B
7、比较a与-a
的大小.
解:
当a>0时,a>-a
;
当a=0时,a=-a
;
当a<0时,a<-a
.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
