第6章 图形的初步知识自我综合评价---2021-2022学年浙教版数学七年级上册阶段综合试卷(word版含答案)
文档属性
| 名称 | 第6章 图形的初步知识自我综合评价---2021-2022学年浙教版数学七年级上册阶段综合试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 183.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 20:45:08 | ||
图片预览


文档简介
自我综合评价(六)
[范围:第6章 图形的初步知识 时间:40分钟 分值:100分]
一、
选择题(每小题3分,共24分)
1.图1是交通禁止驶入标志,组成这个标志的几何图形是
( )
A.圆、长方形 B.圆、长方体
C.球、长方形 D.球、线段
图1
图2
2.如图2,下列说法错误的是
( )
A.直线AB与直线AC是同一条直线
B.线段AB与线段BA是同一条线段
C.射线AB与射线BA是同一条射线
D.射线AB与射线AC是同一条射线
3.在下列日常生活操作中,体现“两点之间线段最短”的是
( )
A.用两根钉子固定一根木条
B.两根木桩拉一直线把树栽成一排
C.把弯路改直可以缩短路程
D.沿桌子的一边看,将桌子排齐
4.如图3,∠AOD=86°,∠AOB=20°,OB平分∠AOC,则∠COD的度数是
( )
A.46°
B.43°
C.40°
D.33°
图3
图4
5.如图4,已知∠AOB=∠COD=90°,则∠1与∠2的关系是
( )
A.互余
B.互补
C.相等
D.无法确定
6.线段AB=12
cm,点C在线段AB上,且AC=BC,M是BC的中点,则AM的长为( )
A.4.5
cm
B.6.5
cm
C.7.5
cm
D.8
cm
7.在同一平面内有4个点,过每两点画一条直线,则直线的条数有
( )
A.1条
B.4条
C.6条
D.1条或4条或6条
8.如果∠1与∠2互补,∠2与∠3互余,那么∠1与∠3的关系是
( )
A.∠1=∠3
B.∠1=180°-∠3
C.∠1=90°+∠3
D.以上都不对
二、填空题(每小题4分,共28分)
9.120°= 周角,平角= 度,32.24°=32° ' ″.?
10.在8:30时,时钟上的时针和分针之间的夹角为 °。?
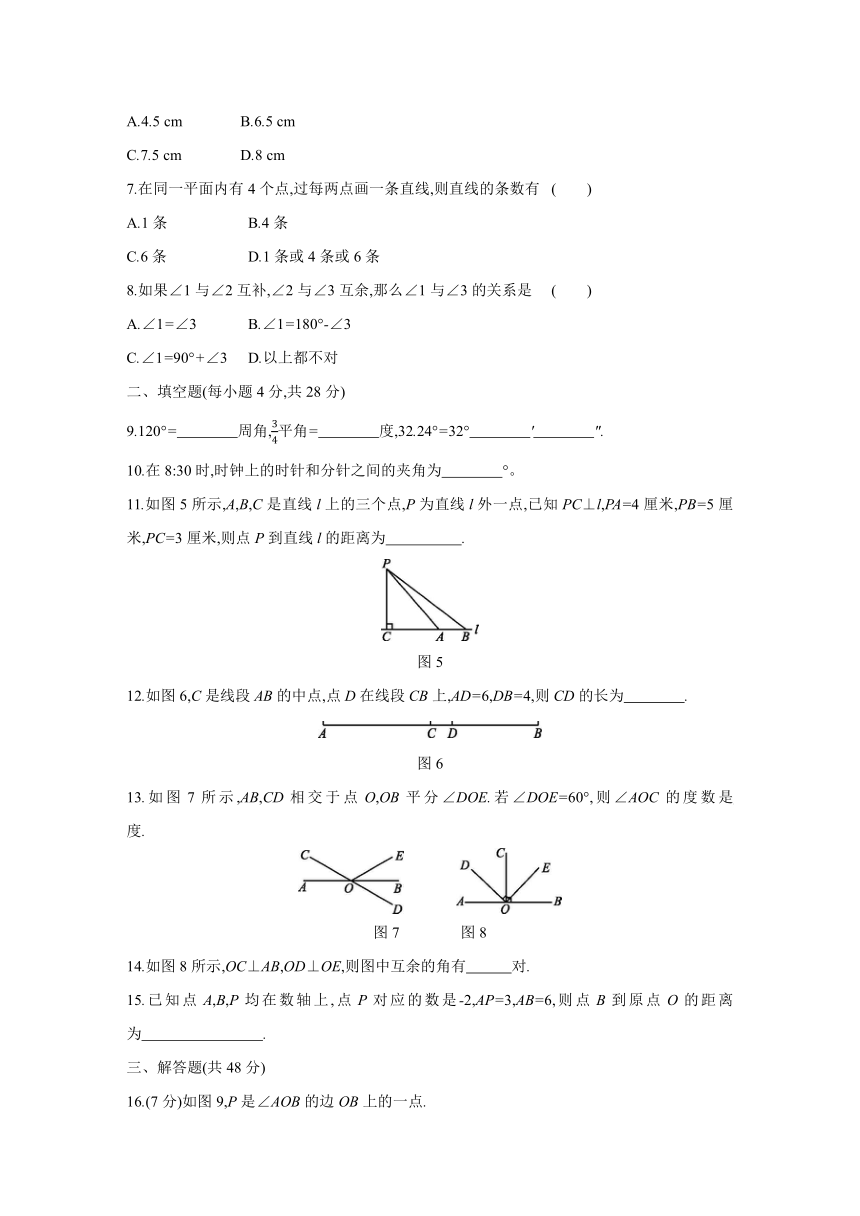
11.如图5所示,A,B,C是直线l上的三个点,P为直线l外一点,已知PC⊥l,PA=4厘米,PB=5厘米,PC=3厘米,则点P到直线l的距离为 .?
图5
12.如图6,C是线段AB的中点,点D在线段CB上,AD=6,DB=4,则CD的长为 .?
图6
13.如图7所示,AB,CD相交于点O,OB平分∠DOE.若∠DOE=60°,则∠AOC的度数是 度.?
图7
图8
14.如图8所示,OC⊥AB,OD⊥OE,则图中互余的角有 对.?
15.已知点A,B,P均在数轴上,点P对应的数是-2,AP=3,AB=6,则点B到原点O的距离为 .?
三、解答题(共48分)
16.(7分)如图9,P是∠AOB的边OB上的一点.
图9
(1)过点P作OB的垂线,交OA于点C;
(2)过点P作OA的垂线,垂足为H;
(3)线段PH的长度是点P到直线 的距离,线段 的长度是点C到直线OB的距离,PC,PH,OC这三条线段的大小关系是 (用“<”连接).?
17.(8分)如图10,直线AB,CD相交于点O,EO⊥AB于点O,∠COE=55°,则∠BOD的度数是多少?
图10
18.(10分)如图11,线段AB=60
cm,C是线段AB上一点,且=,M是线段AB的中点,N是线段BC的中点,求AC,BC,CM,MN的长.
图11
19.(11分)如图12,数轴上点A表示的数为x,点B表示的数为-2,点C表示的数为2x+8.
(1)若将数轴沿点B对折,点A与点C恰好重合,则点A和点C表示的数分别是什么?
(2)若BC=4AB,则点A和点C表示的数分别是什么?
图12
20.(12分)如图13,∠EOD=70°,射线OC,OB分别是∠AOE,∠AOD的平分线.
(1)若∠AOB=20°,求∠BOC的度数;
(2)若∠AOB=α,求∠BOC的度数;
(3)若以OB为钟表上的时针,OC为分针,再过多长时间由B,O,C三点构成的三角形的面积第一次达到最大值?
图13
教师详解详析
1.A 2.C 3.C
4.A [解析]
∵OB平分∠AOC,∠AOB=20°,
∴∠AOC=2∠AOB=40°.
又∵∠AOD=86°,
∴∠COD=∠AOD-∠AOC=86°-40°=46°.
5.B 6.C 7.D 8.C
9. 135 14 24 10.75
11.3厘米 [解析]
点到直线的距离是这个点到这条直线的垂线段的长度.
12.1 13.30
14.4 [解析]
∠AOD与∠DOC,∠DOC与∠COE,∠COE与∠BOE,∠AOD与∠BOE,共4对.
15.1或5或7或11
16.解:(1)(2)如图所示.
(3)OA PC PH17.解:∵OE⊥AB,∴∠AOE=90°.
∵∠COE=55°,∴∠AOC=∠AOE-∠COE=35°.
∵∠BOD与∠AOC是对顶角,∴∠BOD=∠AOC=35°.
18.解:∵=,AB=AC+BC,
∴AC=AB=×60=18,
BC=AB=×60=42.
∵点M是线段AB的中点,N是线段BC的中点,
∴AM=BM=AB=30,BN=CN=BC=×42=21.
∴CM=AM-AC=30-18=12,
MN=BM-BN=30-21=9.
19.解:(1)由题意,得x+(2x+8)=-2×2,
解得x=-4.
2x+8=2×(-4)+8=0.
所以点A表示的数为-4,点C表示的数为0.
(2)由题意,得2x+8-(-2)=4(-2-x),
解得x=-3.
2x+8=2×(-3)+8=2.
所以点A表示的数为-3,点C表示的数为2.
20.解:(1)∵OB为∠AOD的平分线,∠AOB=20°,
∴∠AOD=2∠AOB=40°,
∴∠AOE=∠AOD+∠EOD=40°+70°=110°.
∵OC为∠AOE的平分线,
∴∠AOC=∠AOE=55°,
∴∠BOC=∠AOC-∠AOB=35°.
(2)∵OB为∠AOD的平分线,∠AOB=α,
∴∠AOD=2∠AOB=2α,
∴∠AOE=∠AOD+∠EOD=70°+2α.
∵OC为∠AOE的平分线,
∴∠AOC=∠AOE=35°+α,
∴∠BOC=∠AOC-∠AOB=35°.
(3)当OC⊥OB时,由B,O,C三点构成的三角形的面积最大.设经过t分钟,这三点构成的三角形的面积第一次达到最大值.
由题意得6t-0.5t=35+90,解得t=.
则再经过分钟由B,O,C三点构成的三角形的面积第一次达到最大值.
[范围:第6章 图形的初步知识 时间:40分钟 分值:100分]
一、
选择题(每小题3分,共24分)
1.图1是交通禁止驶入标志,组成这个标志的几何图形是
( )
A.圆、长方形 B.圆、长方体
C.球、长方形 D.球、线段
图1
图2
2.如图2,下列说法错误的是
( )
A.直线AB与直线AC是同一条直线
B.线段AB与线段BA是同一条线段
C.射线AB与射线BA是同一条射线
D.射线AB与射线AC是同一条射线
3.在下列日常生活操作中,体现“两点之间线段最短”的是
( )
A.用两根钉子固定一根木条
B.两根木桩拉一直线把树栽成一排
C.把弯路改直可以缩短路程
D.沿桌子的一边看,将桌子排齐
4.如图3,∠AOD=86°,∠AOB=20°,OB平分∠AOC,则∠COD的度数是
( )
A.46°
B.43°
C.40°
D.33°
图3
图4
5.如图4,已知∠AOB=∠COD=90°,则∠1与∠2的关系是
( )
A.互余
B.互补
C.相等
D.无法确定
6.线段AB=12
cm,点C在线段AB上,且AC=BC,M是BC的中点,则AM的长为( )
A.4.5
cm
B.6.5
cm
C.7.5
cm
D.8
cm
7.在同一平面内有4个点,过每两点画一条直线,则直线的条数有
( )
A.1条
B.4条
C.6条
D.1条或4条或6条
8.如果∠1与∠2互补,∠2与∠3互余,那么∠1与∠3的关系是
( )
A.∠1=∠3
B.∠1=180°-∠3
C.∠1=90°+∠3
D.以上都不对
二、填空题(每小题4分,共28分)
9.120°= 周角,平角= 度,32.24°=32° ' ″.?
10.在8:30时,时钟上的时针和分针之间的夹角为 °。?
11.如图5所示,A,B,C是直线l上的三个点,P为直线l外一点,已知PC⊥l,PA=4厘米,PB=5厘米,PC=3厘米,则点P到直线l的距离为 .?
图5
12.如图6,C是线段AB的中点,点D在线段CB上,AD=6,DB=4,则CD的长为 .?
图6
13.如图7所示,AB,CD相交于点O,OB平分∠DOE.若∠DOE=60°,则∠AOC的度数是 度.?
图7
图8
14.如图8所示,OC⊥AB,OD⊥OE,则图中互余的角有 对.?
15.已知点A,B,P均在数轴上,点P对应的数是-2,AP=3,AB=6,则点B到原点O的距离为 .?
三、解答题(共48分)
16.(7分)如图9,P是∠AOB的边OB上的一点.
图9
(1)过点P作OB的垂线,交OA于点C;
(2)过点P作OA的垂线,垂足为H;
(3)线段PH的长度是点P到直线 的距离,线段 的长度是点C到直线OB的距离,PC,PH,OC这三条线段的大小关系是 (用“<”连接).?
17.(8分)如图10,直线AB,CD相交于点O,EO⊥AB于点O,∠COE=55°,则∠BOD的度数是多少?
图10
18.(10分)如图11,线段AB=60
cm,C是线段AB上一点,且=,M是线段AB的中点,N是线段BC的中点,求AC,BC,CM,MN的长.
图11
19.(11分)如图12,数轴上点A表示的数为x,点B表示的数为-2,点C表示的数为2x+8.
(1)若将数轴沿点B对折,点A与点C恰好重合,则点A和点C表示的数分别是什么?
(2)若BC=4AB,则点A和点C表示的数分别是什么?
图12
20.(12分)如图13,∠EOD=70°,射线OC,OB分别是∠AOE,∠AOD的平分线.
(1)若∠AOB=20°,求∠BOC的度数;
(2)若∠AOB=α,求∠BOC的度数;
(3)若以OB为钟表上的时针,OC为分针,再过多长时间由B,O,C三点构成的三角形的面积第一次达到最大值?
图13
教师详解详析
1.A 2.C 3.C
4.A [解析]
∵OB平分∠AOC,∠AOB=20°,
∴∠AOC=2∠AOB=40°.
又∵∠AOD=86°,
∴∠COD=∠AOD-∠AOC=86°-40°=46°.
5.B 6.C 7.D 8.C
9. 135 14 24 10.75
11.3厘米 [解析]
点到直线的距离是这个点到这条直线的垂线段的长度.
12.1 13.30
14.4 [解析]
∠AOD与∠DOC,∠DOC与∠COE,∠COE与∠BOE,∠AOD与∠BOE,共4对.
15.1或5或7或11
16.解:(1)(2)如图所示.
(3)OA PC PH
∵∠COE=55°,∴∠AOC=∠AOE-∠COE=35°.
∵∠BOD与∠AOC是对顶角,∴∠BOD=∠AOC=35°.
18.解:∵=,AB=AC+BC,
∴AC=AB=×60=18,
BC=AB=×60=42.
∵点M是线段AB的中点,N是线段BC的中点,
∴AM=BM=AB=30,BN=CN=BC=×42=21.
∴CM=AM-AC=30-18=12,
MN=BM-BN=30-21=9.
19.解:(1)由题意,得x+(2x+8)=-2×2,
解得x=-4.
2x+8=2×(-4)+8=0.
所以点A表示的数为-4,点C表示的数为0.
(2)由题意,得2x+8-(-2)=4(-2-x),
解得x=-3.
2x+8=2×(-3)+8=2.
所以点A表示的数为-3,点C表示的数为2.
20.解:(1)∵OB为∠AOD的平分线,∠AOB=20°,
∴∠AOD=2∠AOB=40°,
∴∠AOE=∠AOD+∠EOD=40°+70°=110°.
∵OC为∠AOE的平分线,
∴∠AOC=∠AOE=55°,
∴∠BOC=∠AOC-∠AOB=35°.
(2)∵OB为∠AOD的平分线,∠AOB=α,
∴∠AOD=2∠AOB=2α,
∴∠AOE=∠AOD+∠EOD=70°+2α.
∵OC为∠AOE的平分线,
∴∠AOC=∠AOE=35°+α,
∴∠BOC=∠AOC-∠AOB=35°.
(3)当OC⊥OB时,由B,O,C三点构成的三角形的面积最大.设经过t分钟,这三点构成的三角形的面积第一次达到最大值.
由题意得6t-0.5t=35+90,解得t=.
则再经过分钟由B,O,C三点构成的三角形的面积第一次达到最大值.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
