第一章 三角形的初步知识 自我综合评价 ---2021-2022学年浙教版数学八年级上册(word版含答案)
文档属性
| 名称 | 第一章 三角形的初步知识 自我综合评价 ---2021-2022学年浙教版数学八年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 123.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 20:47:32 | ||
图片预览

文档简介
自我综合评价(一)
[范围:第1章 三角形的初步知识 时间:40分钟 分值:100分]
一、选择题(每小题5分,共30分)
1.长为9,6,5,4的四根木条,选其中三根组成三角形,选法有
( )
A.1种
B.2种
C.3种
D.4种
2.如图1,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为
( )
图1
A.28°
B.38°
C.48°
D.88°
3.下列说法中正确的是
( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
4.如图2,点E,F在线段AC上,DF=BE,∠AFD=∠CEB,下列条件中不能判定△ADF≌△CBE的是
( )
图2
A.∠D=∠B
B.AD=CB
C.AE=CF
D.AD∥BC
5.如图3,在△ABC和△DEB中,点C在BD边上,AC与BE交于点F.若AB=DE,BC=BE,AC=BD,则∠ACB等于
( )
A.∠D
B.∠E
C.2∠ABF
D.∠AFB
图3
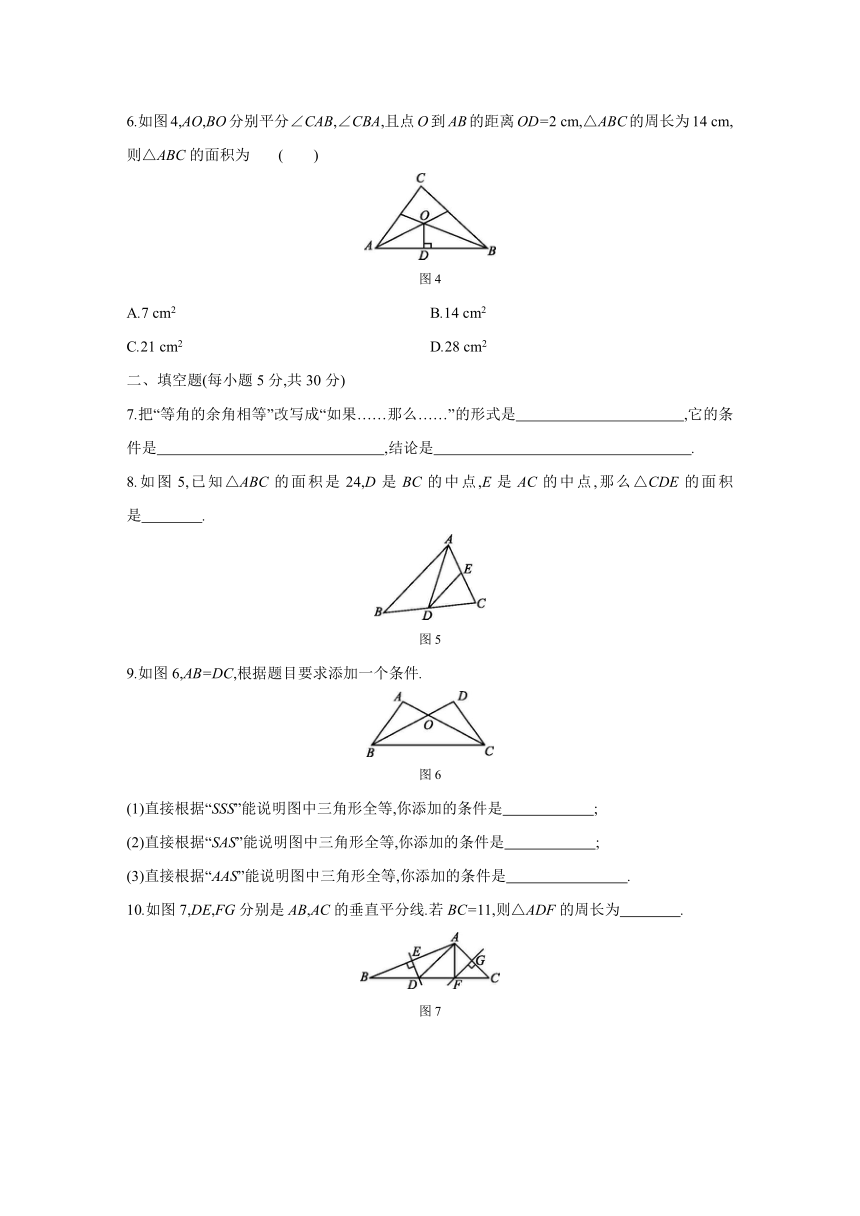
6.如图4,AO,BO分别平分∠CAB,∠CBA,且点O到AB的距离OD=2
cm,△ABC的周长为14
cm,则△ABC的面积为
( )
图4
A.7
cm2
B.14
cm2
C.21
cm2
D.28
cm2
二、填空题(每小题5分,共30分)
7.把“等角的余角相等”改写成“如果……那么……”的形式是 ,它的条件是 ,结论是 .?
8.如图5,已知△ABC的面积是24,D是BC的中点,E是AC的中点,那么△CDE的面积是 .?
图5
9.如图6,AB=DC,根据题目要求添加一个条件.
图6
(1)直接根据“SSS”能说明图中三角形全等,你添加的条件是 ;?
(2)直接根据“SAS”能说明图中三角形全等,你添加的条件是 ;?
(3)直接根据“AAS”能说明图中三角形全等,你添加的条件是 .?
10.如图7,DE,FG分别是AB,AC的垂直平分线.若BC=11,则△ADF的周长为 .?
图7
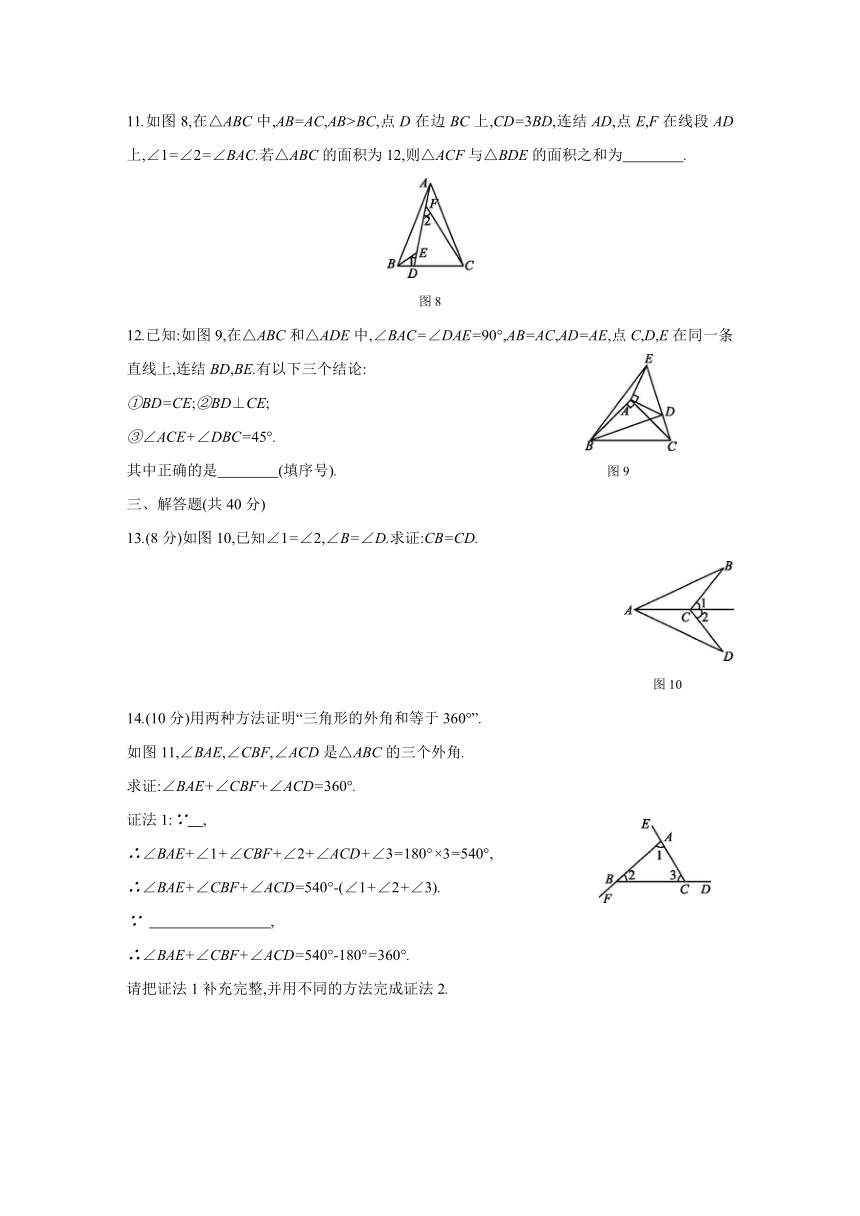
11.如图8,在△ABC中,AB=AC,AB>BC,点D在边BC上,CD=3BD,连结AD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为12,则△ACF与△BDE的面积之和为 .?
图8
12.已知:如图9,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一条直线上,连结BD,BE.有以下三个结论:
①BD=CE;②BD⊥CE;
③∠ACE+∠DBC=45°.
其中正确的是 (填序号).?
图9
三、解答题(共40分)
13.(8分)如图10,已知∠1=∠2,∠B=∠D.求证:CB=CD.
图10
14.(10分)用两种方法证明“三角形的外角和等于360°”.
如图11,∠BAE,∠CBF,∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵ ,?
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°-(∠1+∠2+∠3).
∵
,?
∴∠BAE+∠CBF+∠ACD=540°-180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
15.(10分)如图12,在△ABC中,AD是角平分线,E,F分别为AC,AB上的点,且∠AED+∠AFD=180°.DE与DF有何数量关系?请说明理由.
图12
16.(12分)已知:如图13①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°,AC,BD相交于点P.
(1)求证:①AC=BD;②∠APB=50°.
(2)如图13②,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC,BD相交于点P,则AC与BD间的数量关系为 ,∠APB的度数为 .?
图13
教师详解详析
1.C 2.C 3.C
4.B [解析]
A项,添加∠D=∠B可利用ASA判定△ADF≌△CBE,故此选项不合题意;B项,添加AD=CB不能判定△ADF≌△CBE,故此选项符合题意;C项,添加AE=CF可得AF=CE,可利用SAS判定△ADF≌△CBE,故此选项不合题意;D项,添加AD∥BC可得∠A=∠C,可利用AAS判定△ADF≌△CBE,故此选项不合题意.
故选B.
5.D [解析]
在△ABC与△DEB中,
∵
∴△ABC≌△DEB(SSS),
∴∠ACB=∠EBD.
∵∠AFB是△BFC的外角,
∴∠AFB=∠ACB+∠EBD,
∴∠AFB=2∠ACB,即∠AFB=∠ACB.
故选D.
6.B [解析]
△ABC的面积=(AB+BC+AC)·OD=×14×2=14(cm2).
7.如果两个角相等,那么这两个角的余角相等 两个角相等 这两个角的余角相等
8.6 [解析]
∵D是BC的中点,
∴S△ACD=S△ABC.
∵E是AC的中点,
∴S△CDE=S△ACD=×S△ABC=S△ABC.
∵△ABC的面积是24,
∴△CDE的面积=×24=6.故答案为6.
9.(1)AC=DB
(2)∠ABC=∠DCB
(3)∠ABO=∠DCO(或∠A=∠D)
10.11
11.3 [解析]
∵∠1=∠2=∠BAC,∠1=∠EBA+∠BAE,∠BAC=∠FAC+∠BAE,
∴∠EBA=∠FAC,∠AEB=∠CFA.
在△ABE和△CAF中,∵
∴△ABE≌△CAF(AAS).
∴△ABE的面积=△ACF的面积.
∵CD=3BD,
∴△ABD的面积=△ABC的面积=×12=3,
∴△ACF与△BDE的面积之和=△ABD的面积=3.
故答案为3.
12.①②③ [解析]
∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE.
又∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴BD=CE,故①对.
∴∠ACE=∠ABD.
∵∠ACE+∠DBC=∠ABD+∠DBC=∠ABC=45°,
故③对.
∵∠DBC+∠DCB=∠DBC+∠ABD+∠ACB=90°,
∴BD⊥CE,
故②对.
∴①②③都正确.
13.证明:∵∠1=∠2,∠B=∠D,
∴∠BAC=∠DAC.
在△ABC和△ADC中,∵
∴△ABC≌△ADC(AAS),
∴CB=CD.
14.解:∠BAE+∠1=∠CBF+∠2=∠ACD+∠3=180° ∠1+∠2+∠3=180°
答案不唯一,证法2:过点A
作射线AP,使点P在点A的右侧,且AP∥BD.
∵AP∥BD,
∴∠CBF=∠PAB,∠ACD=∠EAP.
∵∠BAE+∠PAB+∠EAP=360°,
∴∠BAE+∠CBF+∠ACD=360°.
15.解:DE=DF.
理由:如图,过点D作DM⊥AB于点M,DN⊥AC于点N.
∵AD平分∠BAC,
∴DM=DN.
∵∠AED+∠AFD=180°,
∠AED+∠DEN=180°,
∴∠AFD=∠DEN.
在△FMD和△END中,
∵
∴△FMD≌△END,
∴DE=DF.
16.解:(1)证明:①∵∠AOB=∠COD=50°,
∠AOC=∠AOB+∠BOC,∠BOD=∠COD+∠BOC,
∴∠AOC=∠BOD.
在△AOC和△BOD中,∵
∴△AOC≌△BOD,∴AC=BD.
②根据三角形内角和定理可知∠CAO+∠AOB=∠DBO+∠APB,由①,得∠CAO=∠DBO.
∴∠APB=∠AOB=50°.
(2)AC=BD α
[范围:第1章 三角形的初步知识 时间:40分钟 分值:100分]
一、选择题(每小题5分,共30分)
1.长为9,6,5,4的四根木条,选其中三根组成三角形,选法有
( )
A.1种
B.2种
C.3种
D.4种
2.如图1,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为
( )
图1
A.28°
B.38°
C.48°
D.88°
3.下列说法中正确的是
( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
4.如图2,点E,F在线段AC上,DF=BE,∠AFD=∠CEB,下列条件中不能判定△ADF≌△CBE的是
( )
图2
A.∠D=∠B
B.AD=CB
C.AE=CF
D.AD∥BC
5.如图3,在△ABC和△DEB中,点C在BD边上,AC与BE交于点F.若AB=DE,BC=BE,AC=BD,则∠ACB等于
( )
A.∠D
B.∠E
C.2∠ABF
D.∠AFB
图3
6.如图4,AO,BO分别平分∠CAB,∠CBA,且点O到AB的距离OD=2
cm,△ABC的周长为14
cm,则△ABC的面积为
( )
图4
A.7
cm2
B.14
cm2
C.21
cm2
D.28
cm2
二、填空题(每小题5分,共30分)
7.把“等角的余角相等”改写成“如果……那么……”的形式是 ,它的条件是 ,结论是 .?
8.如图5,已知△ABC的面积是24,D是BC的中点,E是AC的中点,那么△CDE的面积是 .?
图5
9.如图6,AB=DC,根据题目要求添加一个条件.
图6
(1)直接根据“SSS”能说明图中三角形全等,你添加的条件是 ;?
(2)直接根据“SAS”能说明图中三角形全等,你添加的条件是 ;?
(3)直接根据“AAS”能说明图中三角形全等,你添加的条件是 .?
10.如图7,DE,FG分别是AB,AC的垂直平分线.若BC=11,则△ADF的周长为 .?
图7
11.如图8,在△ABC中,AB=AC,AB>BC,点D在边BC上,CD=3BD,连结AD,点E,F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为12,则△ACF与△BDE的面积之和为 .?
图8
12.已知:如图9,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E在同一条直线上,连结BD,BE.有以下三个结论:
①BD=CE;②BD⊥CE;
③∠ACE+∠DBC=45°.
其中正确的是 (填序号).?
图9
三、解答题(共40分)
13.(8分)如图10,已知∠1=∠2,∠B=∠D.求证:CB=CD.
图10
14.(10分)用两种方法证明“三角形的外角和等于360°”.
如图11,∠BAE,∠CBF,∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵ ,?
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°-(∠1+∠2+∠3).
∵
,?
∴∠BAE+∠CBF+∠ACD=540°-180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
15.(10分)如图12,在△ABC中,AD是角平分线,E,F分别为AC,AB上的点,且∠AED+∠AFD=180°.DE与DF有何数量关系?请说明理由.
图12
16.(12分)已知:如图13①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50°,AC,BD相交于点P.
(1)求证:①AC=BD;②∠APB=50°.
(2)如图13②,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC,BD相交于点P,则AC与BD间的数量关系为 ,∠APB的度数为 .?
图13
教师详解详析
1.C 2.C 3.C
4.B [解析]
A项,添加∠D=∠B可利用ASA判定△ADF≌△CBE,故此选项不合题意;B项,添加AD=CB不能判定△ADF≌△CBE,故此选项符合题意;C项,添加AE=CF可得AF=CE,可利用SAS判定△ADF≌△CBE,故此选项不合题意;D项,添加AD∥BC可得∠A=∠C,可利用AAS判定△ADF≌△CBE,故此选项不合题意.
故选B.
5.D [解析]
在△ABC与△DEB中,
∵
∴△ABC≌△DEB(SSS),
∴∠ACB=∠EBD.
∵∠AFB是△BFC的外角,
∴∠AFB=∠ACB+∠EBD,
∴∠AFB=2∠ACB,即∠AFB=∠ACB.
故选D.
6.B [解析]
△ABC的面积=(AB+BC+AC)·OD=×14×2=14(cm2).
7.如果两个角相等,那么这两个角的余角相等 两个角相等 这两个角的余角相等
8.6 [解析]
∵D是BC的中点,
∴S△ACD=S△ABC.
∵E是AC的中点,
∴S△CDE=S△ACD=×S△ABC=S△ABC.
∵△ABC的面积是24,
∴△CDE的面积=×24=6.故答案为6.
9.(1)AC=DB
(2)∠ABC=∠DCB
(3)∠ABO=∠DCO(或∠A=∠D)
10.11
11.3 [解析]
∵∠1=∠2=∠BAC,∠1=∠EBA+∠BAE,∠BAC=∠FAC+∠BAE,
∴∠EBA=∠FAC,∠AEB=∠CFA.
在△ABE和△CAF中,∵
∴△ABE≌△CAF(AAS).
∴△ABE的面积=△ACF的面积.
∵CD=3BD,
∴△ABD的面积=△ABC的面积=×12=3,
∴△ACF与△BDE的面积之和=△ABD的面积=3.
故答案为3.
12.①②③ [解析]
∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE.
又∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴BD=CE,故①对.
∴∠ACE=∠ABD.
∵∠ACE+∠DBC=∠ABD+∠DBC=∠ABC=45°,
故③对.
∵∠DBC+∠DCB=∠DBC+∠ABD+∠ACB=90°,
∴BD⊥CE,
故②对.
∴①②③都正确.
13.证明:∵∠1=∠2,∠B=∠D,
∴∠BAC=∠DAC.
在△ABC和△ADC中,∵
∴△ABC≌△ADC(AAS),
∴CB=CD.
14.解:∠BAE+∠1=∠CBF+∠2=∠ACD+∠3=180° ∠1+∠2+∠3=180°
答案不唯一,证法2:过点A
作射线AP,使点P在点A的右侧,且AP∥BD.
∵AP∥BD,
∴∠CBF=∠PAB,∠ACD=∠EAP.
∵∠BAE+∠PAB+∠EAP=360°,
∴∠BAE+∠CBF+∠ACD=360°.
15.解:DE=DF.
理由:如图,过点D作DM⊥AB于点M,DN⊥AC于点N.
∵AD平分∠BAC,
∴DM=DN.
∵∠AED+∠AFD=180°,
∠AED+∠DEN=180°,
∴∠AFD=∠DEN.
在△FMD和△END中,
∵
∴△FMD≌△END,
∴DE=DF.
16.解:(1)证明:①∵∠AOB=∠COD=50°,
∠AOC=∠AOB+∠BOC,∠BOD=∠COD+∠BOC,
∴∠AOC=∠BOD.
在△AOC和△BOD中,∵
∴△AOC≌△BOD,∴AC=BD.
②根据三角形内角和定理可知∠CAO+∠AOB=∠DBO+∠APB,由①,得∠CAO=∠DBO.
∴∠APB=∠AOB=50°.
(2)AC=BD α
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
