2.4 等腰三角形的判定定理---同步课时作业 2021-2022学年浙教版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 2.4 等腰三角形的判定定理---同步课时作业 2021-2022学年浙教版数学八年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 119.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 09:49:00 | ||
图片预览



文档简介
2.4 等腰三角形的判定定理
知识点1 等腰三角形的判定
1.如图1,在△ABC中,∠B=∠C,AB=5,则AC的长为 ( )
图1
A.2 B.3 C.4 D.5
2.[2019·温州龙湾区期中] 具备下列条件的三角形为等腰三角形的是 ( )
A.有两个角分别为20°,120° B.有两个角分别为40°,80°
C.有两个角分别为30°,60° D.有两个角分别为50°,80°
3.亮亮用含30°角的两个完全相同的三角尺拼成如图2所示的图案,他发现图中有等腰三角形,请你帮他找出其中的等腰三角形: .?
图2
4.[教材作业题第4题变式] [2019·温州期中] 如图3,在△ABC中,∠ABC的平分线交AC于点E,过点E作DE∥BC,交AB于点D.若DB=8,则DE= .?
图3
5.完成下面的证明过程:
如图4,∠CAE是△ABC的一个外角,∠1=∠2,AD∥BC,试证明:AB=AC.
图4
证明:∵ AD∥BC(已知),
∴∠1=∠ (两直线平行,同位角相等),?
∠2=∠ ( ).?
又∵∠1=∠2(已知),
∴ = (等量代换),?
∴AB=AC( ).?
6.已知:如图5,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形.
知识点2 等边三角形的判定
7.有下列三角形:①有两个角等于60°;②有一个角是60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高线的等腰三角形.其中是等边三角形的是 ( )
A.①②③ B.①②④
C.①③ D.①②③④
8.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图6①,衣架杆OA=OB=18 cm.若衣架收拢时,∠AOB=60°,如图②,则此时A,B两点之间的距离是 cm.?
图6
9.如图7,在△ABC中,D是AB边上的一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
图7
10.已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OB对称,点P2与点P关于OA对称,则P1,O,P2三点所构成的三角形是 ( )
A.直角三角形
B.钝角三角形
C.等边三角形
D.无法判断三角形的形状
11.如图8,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连结DE,则图中等腰三角形共有( )
图8
A.2个 B.3个 C.4个 D.5个
12.[2019·杭州期中] 已知∠MON=20°,A,B分别是射线OM,ON上的动点(点A,B不与点O重合).若AB⊥OM,在射线ON上有一点C,设∠OAC=x°,则下列x的值不能使△ABC为等腰三角形的是 ( )
A.20 B.45 C.50 D.125
13.[教材作业题第1题变式] 如图9,一艘船早晨5点从灯塔C南偏东42°的A处出发,以16海里/时的速度向正北方向航行,上午8点到达B处,此时灯塔C在船的北偏西84°方向上,则船距离灯塔C 海里.?
图9
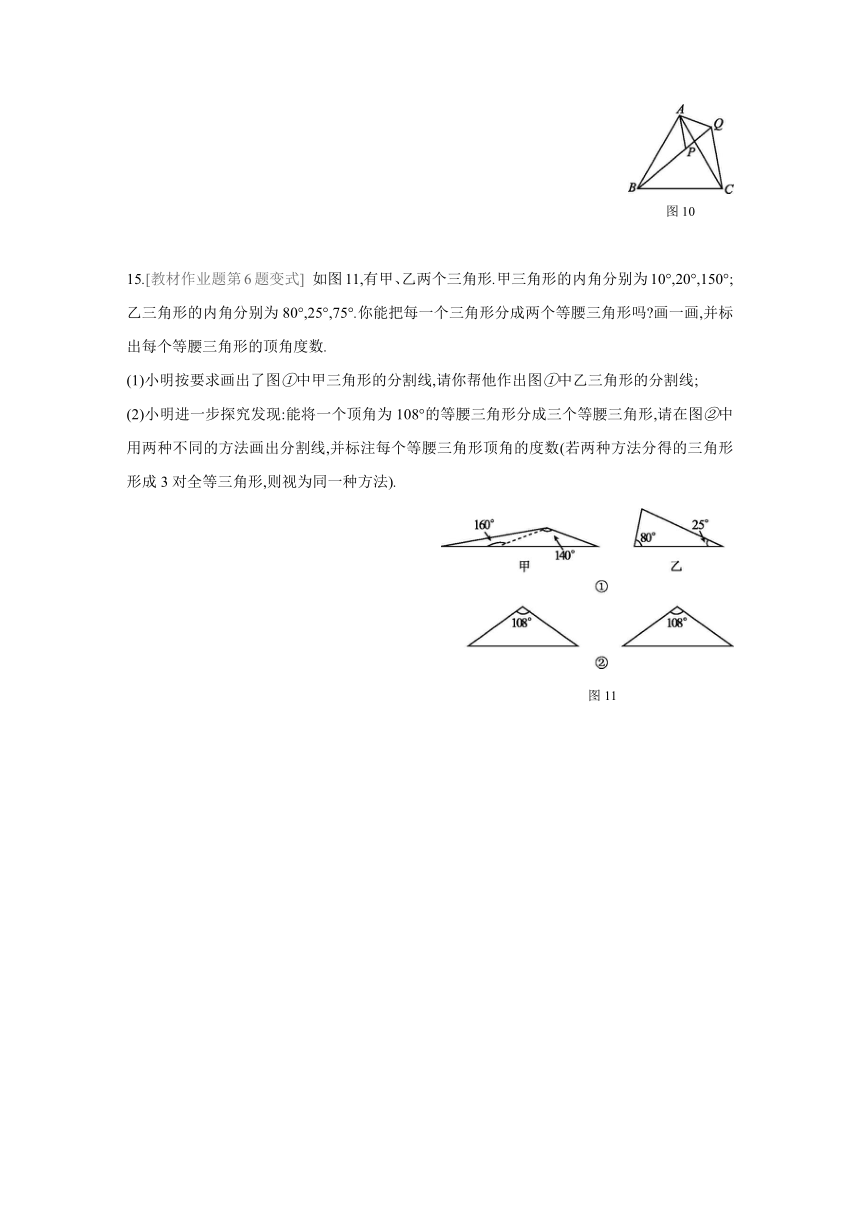
14.如图10,在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,则△APQ是什么形状的三角形?试证明你的结论.
图10
15.[教材作业题第6题变式] 如图11,有甲、乙两个三角形.甲三角形的内角分别为10°,20°,150°;乙三角形的内角分别为80°,25°,75°.你能把每一个三角形分成两个等腰三角形吗?画一画,并标出每个等腰三角形的顶角度数.
(1)小明按要求画出了图①中甲三角形的分割线,请你帮他作出图①中乙三角形的分割线;
(2)小明进一步探究发现:能将一个顶角为108°的等腰三角形分成三个等腰三角形,请在图②中用两种不同的方法画出分割线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形形成3对全等三角形,则视为同一种方法).
图11
教师详解详析
1.D
2.D [解析] A项,有两个角分别为20°,120°的三角形,第三个内角为180°-120°-20°=40°,
∴有两个角分别为20°,120°的三角形不是等腰三角形,选项A不符合题意;
B项,有两个角分别为40°,80°的三角形,第三个内角为180°-40°-80°=60°,
∴有两个角分别为40°,80°的三角形不是等腰三角形,选项B不符合题意;
C项,有两个角分别为30°,60°的三角形,第三个内角为180°-30°-60°=90°,
∴有两个角分别为30°,60°的三角形不是等腰三角形,选项C不符合题意;
D项,有两个角分别为50°,80°的三角形,第三个内角为180°-50°-80°=50°,
有两个角相等,是等腰三角形,
∴有两个角分别为50°,80°的三角形是等腰三角形,选项D符合题意.
故选D.
3.△ABE,△BEC,△CED
4.8 [解析] ∵BE平分∠ABC,
∴∠DBE=∠EBC.
∵DE∥BC,
∴∠DEB=∠EBC,
∴∠DBE=∠DEB,
∴DB=DE.
∵DB=8,
∴DE=8.
故答案为8.
5.B C 两直线平行,内错角相等 ∠B ∠C 等角对等边
6.证明:∵AB=AC,
∴∠B=∠C.
∵DE⊥BC,
∴∠FEC=∠FEB=90°,
∴∠B+∠BDE=∠C+∠F=90°,
∴∠F=∠BDE.
∵∠ADF=∠BDE,
∴∠ADF=∠F,
∴△ADF是等腰三角形.
7.D [解析] ①两个角都为60°,则第三个角也是60°,故其是等边三角形,故正确.
②这是等边三角形的判定定理2,故正确.
③三个外角都相等,则三个内角也都相等,所以该三角形是等边三角形,故正确.
④根据等腰三角形三线合一的性质可得三边都相等,故正确.
8.18 [解析] ∵OA=OB,∠AOB=60°,
∴△OAB是等边三角形,
∴AB=OA=18 cm.
9.证明:∵DC=DB,
∴∠B=∠DCB=30°,
∴∠ADC=∠DCB+∠B=60°.
又∵AD=DC,
∴△ADC是等边三角形.
10.C [解析] 由题意画图.
根据轴对称的性质可知,
OP1=OP=OP2,
∠P1OP2=60°,
∴△P1OP2是等边三角形.
11.D [解析] ∵AB=AC,∴△ABC是等腰三角形.
∵AB=AC,∠A=36°,∴∠ABC=∠C=72°.
∵BD是△ABC的角平分线,
∴∠ABD=∠CBD=12∠ABC=36°,
∴∠A=∠ABD,
∴△ABD是等腰三角形.
在△BCD中,∵∠BDC=180°-∠C-∠CBD=72°,
∴∠C=∠BDC,
∴BD=BC,
∴△BCD是等腰三角形.
∵BE=BC,
∴BE=BD,
∴△BDE是等腰三角形,
∴∠BED=(180°-36°)÷2=72°,
∴∠ADE=∠BED-∠A=36°,
∴∠ADE=∠A,
∴△ADE是等腰三角形.
因此,图中共有5个等腰三角形.故选D.
12.B [解析] ∵AB⊥OM,∴∠OAB=90°.
∵∠MON=20°,
∴∠ABO=70°.
若△ABC为等腰三角形,可分为4种情况.
①当AC=AB时,
∠ACB=∠ABC=70°,
∴x=70-20=50;
②当CA=CB时,
∠CAB=∠ABC=70°,
∴x=90-70=20;
③当AB=BC时,
∠BAC=∠BCA=12(180°-70°)=55°;
④当AB=BC'时,
∠BAC'=∠AC'B=12×70°=35°,
∴∠OAC=x°=180°-20°-35°=125°,
∴x=125.
故选B.
13.48
14.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°.
在△ABP与△ACQ中,
∵AB=AC,∠ABP=∠ACQ,BP=CQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
15.解:(1)按要求作图如下:
(2)(答案不唯一)第一种方法如下(视为同一种):
第二种方法如下:
知识点1 等腰三角形的判定
1.如图1,在△ABC中,∠B=∠C,AB=5,则AC的长为 ( )
图1
A.2 B.3 C.4 D.5
2.[2019·温州龙湾区期中] 具备下列条件的三角形为等腰三角形的是 ( )
A.有两个角分别为20°,120° B.有两个角分别为40°,80°
C.有两个角分别为30°,60° D.有两个角分别为50°,80°
3.亮亮用含30°角的两个完全相同的三角尺拼成如图2所示的图案,他发现图中有等腰三角形,请你帮他找出其中的等腰三角形: .?
图2
4.[教材作业题第4题变式] [2019·温州期中] 如图3,在△ABC中,∠ABC的平分线交AC于点E,过点E作DE∥BC,交AB于点D.若DB=8,则DE= .?
图3
5.完成下面的证明过程:
如图4,∠CAE是△ABC的一个外角,∠1=∠2,AD∥BC,试证明:AB=AC.
图4
证明:∵ AD∥BC(已知),
∴∠1=∠ (两直线平行,同位角相等),?
∠2=∠ ( ).?
又∵∠1=∠2(已知),
∴ = (等量代换),?
∴AB=AC( ).?
6.已知:如图5,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形.
知识点2 等边三角形的判定
7.有下列三角形:①有两个角等于60°;②有一个角是60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高线的等腰三角形.其中是等边三角形的是 ( )
A.①②③ B.①②④
C.①③ D.①②③④
8.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图6①,衣架杆OA=OB=18 cm.若衣架收拢时,∠AOB=60°,如图②,则此时A,B两点之间的距离是 cm.?
图6
9.如图7,在△ABC中,D是AB边上的一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
图7
10.已知∠AOB=30°,点P在∠AOB内部,点P1与点P关于OB对称,点P2与点P关于OA对称,则P1,O,P2三点所构成的三角形是 ( )
A.直角三角形
B.钝角三角形
C.等边三角形
D.无法判断三角形的形状
11.如图8,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连结DE,则图中等腰三角形共有( )
图8
A.2个 B.3个 C.4个 D.5个
12.[2019·杭州期中] 已知∠MON=20°,A,B分别是射线OM,ON上的动点(点A,B不与点O重合).若AB⊥OM,在射线ON上有一点C,设∠OAC=x°,则下列x的值不能使△ABC为等腰三角形的是 ( )
A.20 B.45 C.50 D.125
13.[教材作业题第1题变式] 如图9,一艘船早晨5点从灯塔C南偏东42°的A处出发,以16海里/时的速度向正北方向航行,上午8点到达B处,此时灯塔C在船的北偏西84°方向上,则船距离灯塔C 海里.?
图9
14.如图10,在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,则△APQ是什么形状的三角形?试证明你的结论.
图10
15.[教材作业题第6题变式] 如图11,有甲、乙两个三角形.甲三角形的内角分别为10°,20°,150°;乙三角形的内角分别为80°,25°,75°.你能把每一个三角形分成两个等腰三角形吗?画一画,并标出每个等腰三角形的顶角度数.
(1)小明按要求画出了图①中甲三角形的分割线,请你帮他作出图①中乙三角形的分割线;
(2)小明进一步探究发现:能将一个顶角为108°的等腰三角形分成三个等腰三角形,请在图②中用两种不同的方法画出分割线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形形成3对全等三角形,则视为同一种方法).
图11
教师详解详析
1.D
2.D [解析] A项,有两个角分别为20°,120°的三角形,第三个内角为180°-120°-20°=40°,
∴有两个角分别为20°,120°的三角形不是等腰三角形,选项A不符合题意;
B项,有两个角分别为40°,80°的三角形,第三个内角为180°-40°-80°=60°,
∴有两个角分别为40°,80°的三角形不是等腰三角形,选项B不符合题意;
C项,有两个角分别为30°,60°的三角形,第三个内角为180°-30°-60°=90°,
∴有两个角分别为30°,60°的三角形不是等腰三角形,选项C不符合题意;
D项,有两个角分别为50°,80°的三角形,第三个内角为180°-50°-80°=50°,
有两个角相等,是等腰三角形,
∴有两个角分别为50°,80°的三角形是等腰三角形,选项D符合题意.
故选D.
3.△ABE,△BEC,△CED
4.8 [解析] ∵BE平分∠ABC,
∴∠DBE=∠EBC.
∵DE∥BC,
∴∠DEB=∠EBC,
∴∠DBE=∠DEB,
∴DB=DE.
∵DB=8,
∴DE=8.
故答案为8.
5.B C 两直线平行,内错角相等 ∠B ∠C 等角对等边
6.证明:∵AB=AC,
∴∠B=∠C.
∵DE⊥BC,
∴∠FEC=∠FEB=90°,
∴∠B+∠BDE=∠C+∠F=90°,
∴∠F=∠BDE.
∵∠ADF=∠BDE,
∴∠ADF=∠F,
∴△ADF是等腰三角形.
7.D [解析] ①两个角都为60°,则第三个角也是60°,故其是等边三角形,故正确.
②这是等边三角形的判定定理2,故正确.
③三个外角都相等,则三个内角也都相等,所以该三角形是等边三角形,故正确.
④根据等腰三角形三线合一的性质可得三边都相等,故正确.
8.18 [解析] ∵OA=OB,∠AOB=60°,
∴△OAB是等边三角形,
∴AB=OA=18 cm.
9.证明:∵DC=DB,
∴∠B=∠DCB=30°,
∴∠ADC=∠DCB+∠B=60°.
又∵AD=DC,
∴△ADC是等边三角形.
10.C [解析] 由题意画图.
根据轴对称的性质可知,
OP1=OP=OP2,
∠P1OP2=60°,
∴△P1OP2是等边三角形.
11.D [解析] ∵AB=AC,∴△ABC是等腰三角形.
∵AB=AC,∠A=36°,∴∠ABC=∠C=72°.
∵BD是△ABC的角平分线,
∴∠ABD=∠CBD=12∠ABC=36°,
∴∠A=∠ABD,
∴△ABD是等腰三角形.
在△BCD中,∵∠BDC=180°-∠C-∠CBD=72°,
∴∠C=∠BDC,
∴BD=BC,
∴△BCD是等腰三角形.
∵BE=BC,
∴BE=BD,
∴△BDE是等腰三角形,
∴∠BED=(180°-36°)÷2=72°,
∴∠ADE=∠BED-∠A=36°,
∴∠ADE=∠A,
∴△ADE是等腰三角形.
因此,图中共有5个等腰三角形.故选D.
12.B [解析] ∵AB⊥OM,∴∠OAB=90°.
∵∠MON=20°,
∴∠ABO=70°.
若△ABC为等腰三角形,可分为4种情况.
①当AC=AB时,
∠ACB=∠ABC=70°,
∴x=70-20=50;
②当CA=CB时,
∠CAB=∠ABC=70°,
∴x=90-70=20;
③当AB=BC时,
∠BAC=∠BCA=12(180°-70°)=55°;
④当AB=BC'时,
∠BAC'=∠AC'B=12×70°=35°,
∴∠OAC=x°=180°-20°-35°=125°,
∴x=125.
故选B.
13.48
14.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°.
在△ABP与△ACQ中,
∵AB=AC,∠ABP=∠ACQ,BP=CQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
15.解:(1)按要求作图如下:
(2)(答案不唯一)第一种方法如下(视为同一种):
第二种方法如下:
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
