1.1 认识三角形 ---同步课时作业 2021-2022学年浙教版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 1.1 认识三角形 ---同步课时作业 2021-2022学年浙教版数学八年级上册(Word版 含答案) | 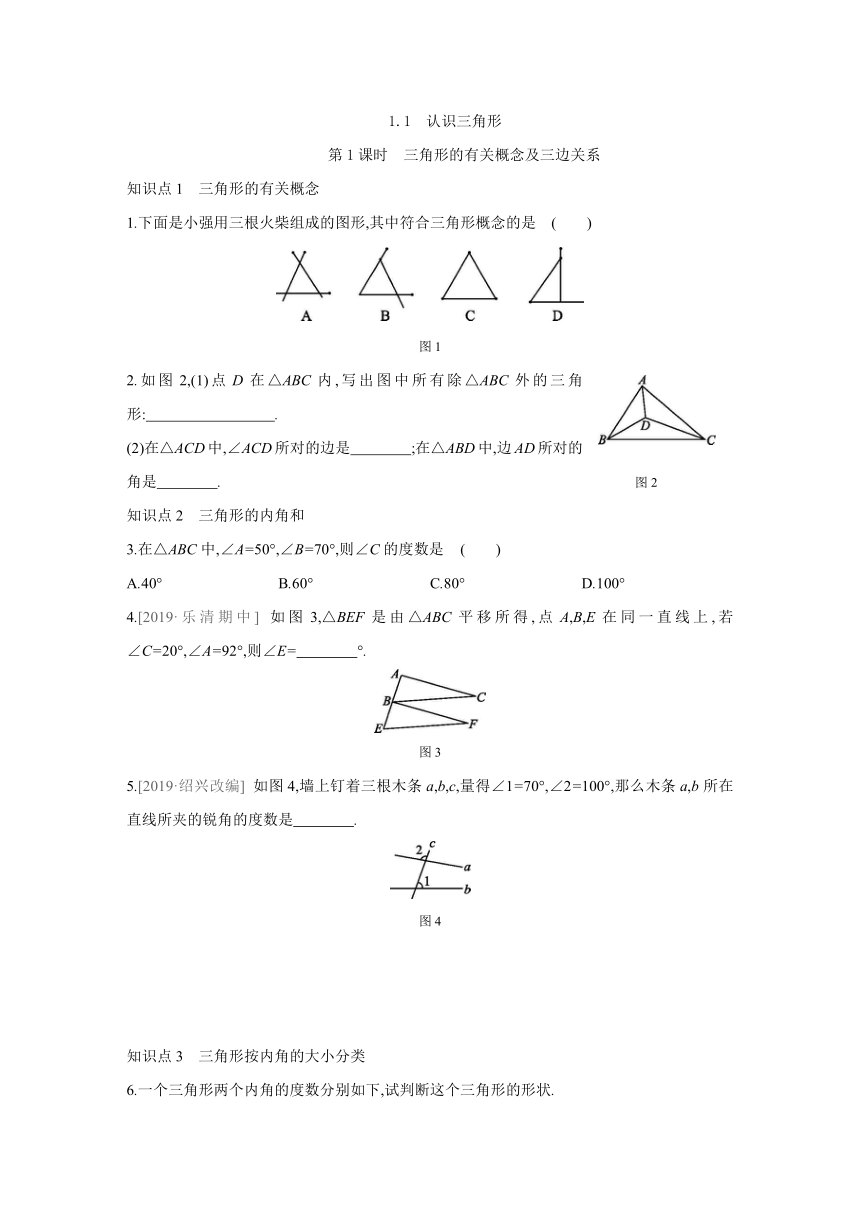 | |
| 格式 | docx | ||
| 文件大小 | 192.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 09:56:51 | ||
图片预览




文档简介
认识三角形
第1课时 三角形的有关概念及三边关系
知识点1 三角形的有关概念
1.下面是小强用三根火柴组成的图形,其中符合三角形概念的是 ( )
图1
41452801047752.如图2,(1)点D在△ABC内,写出图中所有除△ABC外的三角形: .?
(2)在△ACD中,∠ACD所对的边是 ;在△ABD中,边AD所对的角是 .? 图2
知识点2 三角形的内角和
3.在△ABC中,∠A=50°,∠B=70°,则∠C的度数是 ( )
A.40° B.60° C.80° D.100°
4.[2019·乐清期中] 如图3,△BEF是由△ABC平移所得,点A,B,E在同一直线上,若∠C=20°,∠A=92°,则∠E= °.?
图3
5.[2019·绍兴改编] 如图4,墙上钉着三根木条a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角的度数是 .?
图4
知识点3 三角形按内角的大小分类
6.一个三角形两个内角的度数分别如下,试判断这个三角形的形状.
(1)30°和60°: ;?
(2)40°和80°: ;?
(3)50°和20°: .?
7.[2018·杭州滨江区期末改编] △ABC的三个内角∠A,∠B,∠C满足∠A∶∠B∶∠C=1∶2∶3,则这个三角形是 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
8.[教材课内练习第1题变式] 图5中有? 个三角形,其中 是锐角三角形, 是直角三角形, 是钝角三角形.?
图5
知识点4 三角形的三边关系
9.在图6所示的△ABC中,有AB+AC BC(填“>”“<”或“=”),理由是 ,?
这个性质是由数学基本事实 得到的.?
图6
10.[2019·台州] 下列长度的三条线段,能组成三角形的是 ( )
A.3,4,8 B.5,6,10 C.5,5,11 D.5,6,11
11.[2019·温州泰顺县模拟] 现有2根长分别为1米,4米的钢管,若再选一根钢管,使三根钢管首尾顺次相接,焊成一个三角形的固定架(接头不计),则下列符合条件的钢管长为 ( )
A.2米 B.3米 C.4米 D.5米
12.[教材课内练习第3题变式] 如图7,在△ABC中,D是AB的中点,连结CD,
397383017145在下列空格中填写“>”“<”或“=”.
(1)CD+AD AC;?
(2)CD-DB BC;?
(3)2BD AC+BC.? 图7
13.[教材作业题第2题变式] 下列长度的三条线段能否组成三角形?为什么?
(1)3,6,8; (2)4,7,11; (3)2,8,5.
14.[2019·慈溪期末] △ABC的内角分别为∠A,∠B,∠C,下列能判定△ABC是直角三角形的条件是 ( )
A.∠A=2∠B=3∠C
B.∠C=2∠B
C.∠A∶∠B∶∠C=3∶4∶5
D.∠A+∠B=∠C
15.[2019·宁波鄞州区一模] 三角形的两边长分别是4,7,则第三边长不可能是 ( )
A.4 B.6 C.10 D.12
16.已知△ABC的三边长分别是a,b,c,化简|a+b-c|-|b-a-c|的结果是 ( )
A.2b-2c B.-2b
C.2a+2b D.2a
17.如图8,在△ABC中,∠DBC=13∠ABC,∠DCB=13∠ACB,∠A=45°,则∠BDC= °.?
图8
18.如图9,某油田有四个油井A,B,C,D,如果要建一个维修站H,使这个维修站到这四个油井的距离之和最短,请你找出点H的位置,并说明理由.
图9
19.观察图10并探索下列问题:
(1)如图①,在△ABC中,P为BC边上一点,则BP+PC AB+AC(填“<”“>”或“=”);?
(2)将(1)中的点P移到△ABC内,得到图②,试比较△BPC的周长与△ABC的周长的大小关系.
图10
1.1 认识三角形
第2课时 三角形中的重要线段
知识点1 三角形的角平分线
1.已知AD是△ABC的角平分线,那么∠BAD= =12 .?
4383405990602.如图11所示,∠1=∠2,∠3=∠4,下列结论中错误的是 ( )
A.BD是△ABC的角平分线 B.CE是△BCD的角平分线
C.∠3=12∠ACB D.CE是△ABC的角平分线
知识点2 三角形的中线 图11
3.已知AE是△ABC的中线,那么BE= = BC.?
4.已知AD是△ABC的中线,且AB=3 cm,AC=6 cm,BD=2 cm,则△ABC的周长= cm.?
知识点3 三角形的高线
5.[2019·温岭期中] 如图12,在△ABC中,画出AC边上的高,正确的图形是 ( )
图12
6.在△ABC中,BD是AC边上的高.若△ABC的面积为4,AC=4,则BD= .?
7.如图13,∠1=∠2,G为AD的中点,连结BG并延长交AC于点E,F为AB上的一点,CF⊥AD于点H.下列判断正确的是 ( )
图13
2554605228600A.AD是△ABE的角平分线
B.BE是△ABD的边AD上的中线
C.CH为△ACD的边AD上的高
D.AH为△ABC的角平分线
图11
8.已知AD是△ABC的中线.
(1)若△ABD的周长为25,AB比AC长6,则△ADC的周长为 ;?
(2)若S△ABD=8,则S△ACD= .?
9.如图14,在△ABC中,BD是AC边上的中线,AE是△ABD中BD边上的中线.若△ABC的面积为S,则△AED的面积为 .?
图14
10.(1)已知:如图15(a),在△ABC中,AD,AE分别是△ABC的高线和角平分线.若∠B=30°,∠C=50°,求∠DAE的度数.
(2)如图15(b),已知AF平分∠BAC,交边BC于点E,过点F作FD⊥BC于点D.若∠B=x°,∠C=(x+36)°.
①求∠CAE的度数(用含x的代数式表示);
②求∠F的度数.
图15
教师详解详析
1.C [解析] 三角形是由不在同一条直线上的三条线段首尾顺次相接所组成的图形.故选C.
2.(1)△ABD,△ACD,△BCD (2)AD ∠ABD
3.B
4.68 [解析] 在△ABC中,∠ABC=180°-∠C-∠A=180°-20°-92°=68°.
∵△BEF是由△ABC平移所得,
∴∠E=∠ABC=68°.
故答案为68.
5.10° [解析] 如图,∵∠3=∠2=100°,∴木条a,b所在直线所夹的锐角=180°-100°-70°=10°.
6.(1)直角三角形 (2)锐角三角形
(3)钝角三角形
[解析] (1)根据“三角形三个内角的和等于180°”得第三个角为90°,因此该三角形是直角三角形;
(2)根据“三角形三个内角的和等于180°”得第三个角为60°,因此该三角形是锐角三角形;
(3)根据“三角形三个内角的和等于180°”得第三个角为110°,因此该三角形是钝角三角形.
7.C [解析] ∵∠A∶∠B∶∠C=1∶2∶3,
∴设∠A,∠B,∠C分别为k,2k,3k.
由题意,得k+2k+3k=180°,
解得k=30°,
∴∠C=3×30°=90°,
∴这个三角形是直角三角形.
故选C.
8.6 △ADC △ABE,△ADE,△AEC,△ABC
△ABD [解析] 三角形有△ABD,△ABE,△ABC,△ADE,△ADC,△AEC,共6个,△ADC是锐角三角形,△ABE,△ADE,△AEC,△ABC是直角三角形,△ABD是钝角三角形.
故答案为6,△ADC,△ABE,△ADE,△AEC,△ABC,△ABD.
9.> 三角形任何两边的和大于第三边 两点之间线段最短
10.B [解析] A选项,3+4=7<8,两边之和小于第三边,故不能组成三角形;B选项,5+6=11>10,10-5<6,两边之和大于第三边,两边之差小于第三边,故能组成三角形;C选项,5+5=10<11,两边之和小于第三边,故不能组成三角形;D选项,5+6=11,两边之和等于第三边,故不能组成三角形.
故选B.
11.C [解析] A选项,∵2+1=3<4,∴2米不符合题意;B选项,∵3+1=4,∴3米不符合题意;C选项,∵4+1=5>4,∴4米符合题意;D选项,∵4+1=5,∴5米不符合题意.
故选C.
12.(1)> (2)< (3)<
13.解:(1)能.理由:
∵最长线段长是8,3+6>8,∴能组成三角形.
(2)不能.理由:
∵最长线段长是11,4+7=11,∴不能组成三角形.
(3)不能.理由:
∵最长线段长是8,2+5<8,∴不能组成三角形.
14.D [解析] A项,∵∠A+∠B+∠C=180°,∠A=2∠B=3∠C,∴13∠A+12∠A+∠A=180°,解得∠A=1080°11≠90°,不符合题意;B项,∵∠A+∠B+∠C=180°,∠C=2∠B,不能得出∠C=90°,不符合题意;C项,∵∠A+∠B+∠C=180°,∠A∶∠B∶∠C=3∶4∶5,∴∠C=75°≠90°,不符合题意;D项,∵∠A+∠B+∠C=180°,∠A+∠B=∠C,∴∠C=90°,符合题意.
故选D.
15.D [解析] 根据三角形的三边关系,得7-4<第三边长<7+4,
解得3<第三边长<11.
故第三边长不可能是12.
故选D.
16.A [解析] ∵△ABC的三边长分别是a,b,c,
∴a+b>c,b-a∴a+b-c>0,b-a-c<0,
∴|a+b-c|-|b-a-c|=a+b-c-(-b+a+c)=a+b-c+b-a-c=2b-2c.故选A.
17.135 [解析] 因为∠A=45°,所以∠ABC+∠ACB=135°.因为∠DBC=13∠ABC,∠DCB=13∠ACB,所以∠DBC+∠DCB=13(∠ABC+∠ACB)=13×135°=45°.因此,∠BDC=180°-(∠DBC+∠DCB)=180°-45°=135°.
18.解:如图,连结AC,BD,其交点即为H.
310705545720理由:任选点H',连结AH',H'B,H'C,DH',如图.
∵AH'+H'C>AC,DH'+H'B>BD,
∴AH'+H'C+DH'+H'B>AC+BD.
∵AC=AH+HC,BD=DH+HB,
∴AH'+H'C+DH'+H'B>AH+HC+DH+HB,
∴点H就是所要找的点.
19.解:(1)<
2611755241935(2)如图,延长BP交AC于点M.
在△ABM中,BP+PM在△PMC中,PC①②两式相加,得BP+PC∴BP+PC+BC即△BPC的周长<△ABC的周长.
教师详解详析
1.∠CAD ∠BAC
2.D [解析] 由∠1=∠2,∠3=∠4,根据角平分线的定义,可知BD是△ABC的角平分线,CE是△BCD的角平分线,所以选项A,B正确;因为∠3=∠4=12∠ACB,所以选项C正确;CE不是△ABC的角平分线,三角形的角平分线是三角形的内角平分线与对边相交,这个角的顶点与交点之间的线段,所以选项D错误.故选D.
3.CE 12
4.13 [解析] 由AD是△ABC的中线,BD=2 cm,得BC=2BD=4(cm).
由三角形的周长公式,得
△ABC的周长=AB+AC+BC=3+6+4=13(cm).
故答案为13.
5.D [解析] 根据三角形高线的定义,AC边上的高是过点B向AC作垂线,垂足为D,纵观各图形,选项A,B,C都不符合高线的定义,选项D符合高线的定义.
故选D.
6.2
7.C [解析] A项,根据三角形的角平分线的概念,知AG是△ABE的角平分线,故本选项错误;B项,根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故本选项错误;C项,根据三角形的高的概念,知CH为△ACD的边AD上的高,故本选项正确;D项,根据三角形的角平分线的概念,知AD是△ABC的角平分线,故本选项错误.
故选C.
8.(1)19 [解析] 因为AD是△ABC的中线,所以BD=CD.又因为AD=AD,AB比AC长6,所以△ADC的周长为25-6=19.
(2)8
9.14S
10.解:(1)∵∠B=30°,∠C=50°,
∴∠CAB=180°-∠B-∠C=100°.
∵AE是△ABC的角平分线,
∴∠CAE=12∠CAB=50°.
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠CAD=180°-∠ADC-∠C=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°.
(2)①∵AF平分∠BAC,∴∠CAE=∠BAE.
∵∠B=x°,∠C=(x+36)°,
∴∠CAE=12×[180°-x°-(x+36)°]=(72-x)°.
②∵∠FED=∠AEC=180°-∠CAE-∠C=
180°-(72-x)°-(x+36)°=72°,
又∵FD⊥BC,
∴∠F=180°-∠FDE-∠FED=180°-90°-72°=18°.
第1课时 三角形的有关概念及三边关系
知识点1 三角形的有关概念
1.下面是小强用三根火柴组成的图形,其中符合三角形概念的是 ( )
图1
41452801047752.如图2,(1)点D在△ABC内,写出图中所有除△ABC外的三角形: .?
(2)在△ACD中,∠ACD所对的边是 ;在△ABD中,边AD所对的角是 .? 图2
知识点2 三角形的内角和
3.在△ABC中,∠A=50°,∠B=70°,则∠C的度数是 ( )
A.40° B.60° C.80° D.100°
4.[2019·乐清期中] 如图3,△BEF是由△ABC平移所得,点A,B,E在同一直线上,若∠C=20°,∠A=92°,则∠E= °.?
图3
5.[2019·绍兴改编] 如图4,墙上钉着三根木条a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角的度数是 .?
图4
知识点3 三角形按内角的大小分类
6.一个三角形两个内角的度数分别如下,试判断这个三角形的形状.
(1)30°和60°: ;?
(2)40°和80°: ;?
(3)50°和20°: .?
7.[2018·杭州滨江区期末改编] △ABC的三个内角∠A,∠B,∠C满足∠A∶∠B∶∠C=1∶2∶3,则这个三角形是 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.不能确定
8.[教材课内练习第1题变式] 图5中有? 个三角形,其中 是锐角三角形, 是直角三角形, 是钝角三角形.?
图5
知识点4 三角形的三边关系
9.在图6所示的△ABC中,有AB+AC BC(填“>”“<”或“=”),理由是 ,?
这个性质是由数学基本事实 得到的.?
图6
10.[2019·台州] 下列长度的三条线段,能组成三角形的是 ( )
A.3,4,8 B.5,6,10 C.5,5,11 D.5,6,11
11.[2019·温州泰顺县模拟] 现有2根长分别为1米,4米的钢管,若再选一根钢管,使三根钢管首尾顺次相接,焊成一个三角形的固定架(接头不计),则下列符合条件的钢管长为 ( )
A.2米 B.3米 C.4米 D.5米
12.[教材课内练习第3题变式] 如图7,在△ABC中,D是AB的中点,连结CD,
397383017145在下列空格中填写“>”“<”或“=”.
(1)CD+AD AC;?
(2)CD-DB BC;?
(3)2BD AC+BC.? 图7
13.[教材作业题第2题变式] 下列长度的三条线段能否组成三角形?为什么?
(1)3,6,8; (2)4,7,11; (3)2,8,5.
14.[2019·慈溪期末] △ABC的内角分别为∠A,∠B,∠C,下列能判定△ABC是直角三角形的条件是 ( )
A.∠A=2∠B=3∠C
B.∠C=2∠B
C.∠A∶∠B∶∠C=3∶4∶5
D.∠A+∠B=∠C
15.[2019·宁波鄞州区一模] 三角形的两边长分别是4,7,则第三边长不可能是 ( )
A.4 B.6 C.10 D.12
16.已知△ABC的三边长分别是a,b,c,化简|a+b-c|-|b-a-c|的结果是 ( )
A.2b-2c B.-2b
C.2a+2b D.2a
17.如图8,在△ABC中,∠DBC=13∠ABC,∠DCB=13∠ACB,∠A=45°,则∠BDC= °.?
图8
18.如图9,某油田有四个油井A,B,C,D,如果要建一个维修站H,使这个维修站到这四个油井的距离之和最短,请你找出点H的位置,并说明理由.
图9
19.观察图10并探索下列问题:
(1)如图①,在△ABC中,P为BC边上一点,则BP+PC AB+AC(填“<”“>”或“=”);?
(2)将(1)中的点P移到△ABC内,得到图②,试比较△BPC的周长与△ABC的周长的大小关系.
图10
1.1 认识三角形
第2课时 三角形中的重要线段
知识点1 三角形的角平分线
1.已知AD是△ABC的角平分线,那么∠BAD= =12 .?
4383405990602.如图11所示,∠1=∠2,∠3=∠4,下列结论中错误的是 ( )
A.BD是△ABC的角平分线 B.CE是△BCD的角平分线
C.∠3=12∠ACB D.CE是△ABC的角平分线
知识点2 三角形的中线 图11
3.已知AE是△ABC的中线,那么BE= = BC.?
4.已知AD是△ABC的中线,且AB=3 cm,AC=6 cm,BD=2 cm,则△ABC的周长= cm.?
知识点3 三角形的高线
5.[2019·温岭期中] 如图12,在△ABC中,画出AC边上的高,正确的图形是 ( )
图12
6.在△ABC中,BD是AC边上的高.若△ABC的面积为4,AC=4,则BD= .?
7.如图13,∠1=∠2,G为AD的中点,连结BG并延长交AC于点E,F为AB上的一点,CF⊥AD于点H.下列判断正确的是 ( )
图13
2554605228600A.AD是△ABE的角平分线
B.BE是△ABD的边AD上的中线
C.CH为△ACD的边AD上的高
D.AH为△ABC的角平分线
图11
8.已知AD是△ABC的中线.
(1)若△ABD的周长为25,AB比AC长6,则△ADC的周长为 ;?
(2)若S△ABD=8,则S△ACD= .?
9.如图14,在△ABC中,BD是AC边上的中线,AE是△ABD中BD边上的中线.若△ABC的面积为S,则△AED的面积为 .?
图14
10.(1)已知:如图15(a),在△ABC中,AD,AE分别是△ABC的高线和角平分线.若∠B=30°,∠C=50°,求∠DAE的度数.
(2)如图15(b),已知AF平分∠BAC,交边BC于点E,过点F作FD⊥BC于点D.若∠B=x°,∠C=(x+36)°.
①求∠CAE的度数(用含x的代数式表示);
②求∠F的度数.
图15
教师详解详析
1.C [解析] 三角形是由不在同一条直线上的三条线段首尾顺次相接所组成的图形.故选C.
2.(1)△ABD,△ACD,△BCD (2)AD ∠ABD
3.B
4.68 [解析] 在△ABC中,∠ABC=180°-∠C-∠A=180°-20°-92°=68°.
∵△BEF是由△ABC平移所得,
∴∠E=∠ABC=68°.
故答案为68.
5.10° [解析] 如图,∵∠3=∠2=100°,∴木条a,b所在直线所夹的锐角=180°-100°-70°=10°.
6.(1)直角三角形 (2)锐角三角形
(3)钝角三角形
[解析] (1)根据“三角形三个内角的和等于180°”得第三个角为90°,因此该三角形是直角三角形;
(2)根据“三角形三个内角的和等于180°”得第三个角为60°,因此该三角形是锐角三角形;
(3)根据“三角形三个内角的和等于180°”得第三个角为110°,因此该三角形是钝角三角形.
7.C [解析] ∵∠A∶∠B∶∠C=1∶2∶3,
∴设∠A,∠B,∠C分别为k,2k,3k.
由题意,得k+2k+3k=180°,
解得k=30°,
∴∠C=3×30°=90°,
∴这个三角形是直角三角形.
故选C.
8.6 △ADC △ABE,△ADE,△AEC,△ABC
△ABD [解析] 三角形有△ABD,△ABE,△ABC,△ADE,△ADC,△AEC,共6个,△ADC是锐角三角形,△ABE,△ADE,△AEC,△ABC是直角三角形,△ABD是钝角三角形.
故答案为6,△ADC,△ABE,△ADE,△AEC,△ABC,△ABD.
9.> 三角形任何两边的和大于第三边 两点之间线段最短
10.B [解析] A选项,3+4=7<8,两边之和小于第三边,故不能组成三角形;B选项,5+6=11>10,10-5<6,两边之和大于第三边,两边之差小于第三边,故能组成三角形;C选项,5+5=10<11,两边之和小于第三边,故不能组成三角形;D选项,5+6=11,两边之和等于第三边,故不能组成三角形.
故选B.
11.C [解析] A选项,∵2+1=3<4,∴2米不符合题意;B选项,∵3+1=4,∴3米不符合题意;C选项,∵4+1=5>4,∴4米符合题意;D选项,∵4+1=5,∴5米不符合题意.
故选C.
12.(1)> (2)< (3)<
13.解:(1)能.理由:
∵最长线段长是8,3+6>8,∴能组成三角形.
(2)不能.理由:
∵最长线段长是11,4+7=11,∴不能组成三角形.
(3)不能.理由:
∵最长线段长是8,2+5<8,∴不能组成三角形.
14.D [解析] A项,∵∠A+∠B+∠C=180°,∠A=2∠B=3∠C,∴13∠A+12∠A+∠A=180°,解得∠A=1080°11≠90°,不符合题意;B项,∵∠A+∠B+∠C=180°,∠C=2∠B,不能得出∠C=90°,不符合题意;C项,∵∠A+∠B+∠C=180°,∠A∶∠B∶∠C=3∶4∶5,∴∠C=75°≠90°,不符合题意;D项,∵∠A+∠B+∠C=180°,∠A+∠B=∠C,∴∠C=90°,符合题意.
故选D.
15.D [解析] 根据三角形的三边关系,得7-4<第三边长<7+4,
解得3<第三边长<11.
故第三边长不可能是12.
故选D.
16.A [解析] ∵△ABC的三边长分别是a,b,c,
∴a+b>c,b-a
∴|a+b-c|-|b-a-c|=a+b-c-(-b+a+c)=a+b-c+b-a-c=2b-2c.故选A.
17.135 [解析] 因为∠A=45°,所以∠ABC+∠ACB=135°.因为∠DBC=13∠ABC,∠DCB=13∠ACB,所以∠DBC+∠DCB=13(∠ABC+∠ACB)=13×135°=45°.因此,∠BDC=180°-(∠DBC+∠DCB)=180°-45°=135°.
18.解:如图,连结AC,BD,其交点即为H.
310705545720理由:任选点H',连结AH',H'B,H'C,DH',如图.
∵AH'+H'C>AC,DH'+H'B>BD,
∴AH'+H'C+DH'+H'B>AC+BD.
∵AC=AH+HC,BD=DH+HB,
∴AH'+H'C+DH'+H'B>AH+HC+DH+HB,
∴点H就是所要找的点.
19.解:(1)<
2611755241935(2)如图,延长BP交AC于点M.
在△ABM中,BP+PM
教师详解详析
1.∠CAD ∠BAC
2.D [解析] 由∠1=∠2,∠3=∠4,根据角平分线的定义,可知BD是△ABC的角平分线,CE是△BCD的角平分线,所以选项A,B正确;因为∠3=∠4=12∠ACB,所以选项C正确;CE不是△ABC的角平分线,三角形的角平分线是三角形的内角平分线与对边相交,这个角的顶点与交点之间的线段,所以选项D错误.故选D.
3.CE 12
4.13 [解析] 由AD是△ABC的中线,BD=2 cm,得BC=2BD=4(cm).
由三角形的周长公式,得
△ABC的周长=AB+AC+BC=3+6+4=13(cm).
故答案为13.
5.D [解析] 根据三角形高线的定义,AC边上的高是过点B向AC作垂线,垂足为D,纵观各图形,选项A,B,C都不符合高线的定义,选项D符合高线的定义.
故选D.
6.2
7.C [解析] A项,根据三角形的角平分线的概念,知AG是△ABE的角平分线,故本选项错误;B项,根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故本选项错误;C项,根据三角形的高的概念,知CH为△ACD的边AD上的高,故本选项正确;D项,根据三角形的角平分线的概念,知AD是△ABC的角平分线,故本选项错误.
故选C.
8.(1)19 [解析] 因为AD是△ABC的中线,所以BD=CD.又因为AD=AD,AB比AC长6,所以△ADC的周长为25-6=19.
(2)8
9.14S
10.解:(1)∵∠B=30°,∠C=50°,
∴∠CAB=180°-∠B-∠C=100°.
∵AE是△ABC的角平分线,
∴∠CAE=12∠CAB=50°.
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠CAD=180°-∠ADC-∠C=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°.
(2)①∵AF平分∠BAC,∴∠CAE=∠BAE.
∵∠B=x°,∠C=(x+36)°,
∴∠CAE=12×[180°-x°-(x+36)°]=(72-x)°.
②∵∠FED=∠AEC=180°-∠CAE-∠C=
180°-(72-x)°-(x+36)°=72°,
又∵FD⊥BC,
∴∠F=180°-∠FDE-∠FED=180°-90°-72°=18°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
