2.8 直角三角形全等的判定---同步课时作业 2021-2022学年浙教版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 2.8 直角三角形全等的判定---同步课时作业 2021-2022学年浙教版数学八年级上册(Word版 含答案) | 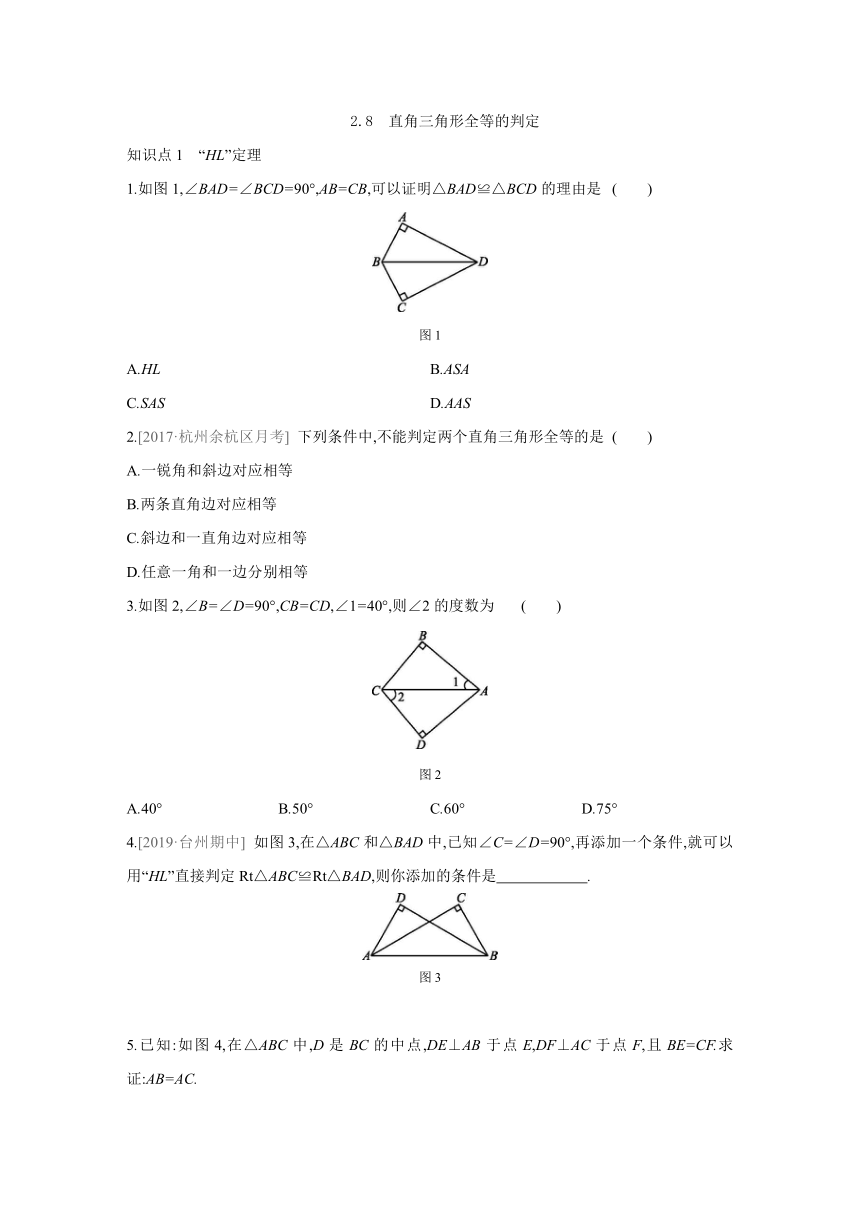 | |
| 格式 | docx | ||
| 文件大小 | 133.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 09:59:48 | ||
图片预览



文档简介
2.8 直角三角形全等的判定
知识点1 “HL”定理
1.如图1,∠BAD=∠BCD=90°,AB=CB,可以证明△BAD≌△BCD的理由是 ( )
图1
A.HL B.ASA
C.SAS D.AAS
2.[2017·杭州余杭区月考] 下列条件中,不能判定两个直角三角形全等的是 ( )
A.一锐角和斜边对应相等
B.两条直角边对应相等
C.斜边和一直角边对应相等
D.任意一角和一边分别相等
3.如图2,∠B=∠D=90°,CB=CD,∠1=40°,则∠2的度数为 ( )
图2
A.40° B.50° C.60° D.75°
4.[2019·台州期中] 如图3,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”直接判定Rt△ABC≌Rt△BAD,则你添加的条件是 .?
图3
5.已知:如图4,在△ABC中,D是BC的中点,DE⊥AB于点E,DF⊥AC于点F,且BE=CF.求证:AB=AC.
图4
完成下面的证明过程.
证明:∵DE⊥AB,DF⊥AC( ),?
∴∠BED=∠CFD= °.?
∵D是BC的中点,
∴BD= .?
又∵BE=CF,
∴Rt△BDE≌Rt△CDF( ),?
∴∠B=∠C( ),?
∴AB=AC( ).?
知识点2 角平分线性质定理的逆定理
6.[2019·衢州期中] 如图5,∠AOB=50°,CD⊥OA于点D,CE⊥OB于点E,且CD=CE,则∠DOC= °.?
图5
7.已知:如图6,OC是∠AOB内部的一条射线,P是射线OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D,E.有下列条件:①∠AOC=∠BOC;②PD=PE;③OD=OE;④∠DPO=∠EPO.其中,能判定OC是∠AOB的平分线的有 ( )
图6
A.1个 B.2个 C.3个 D.4个
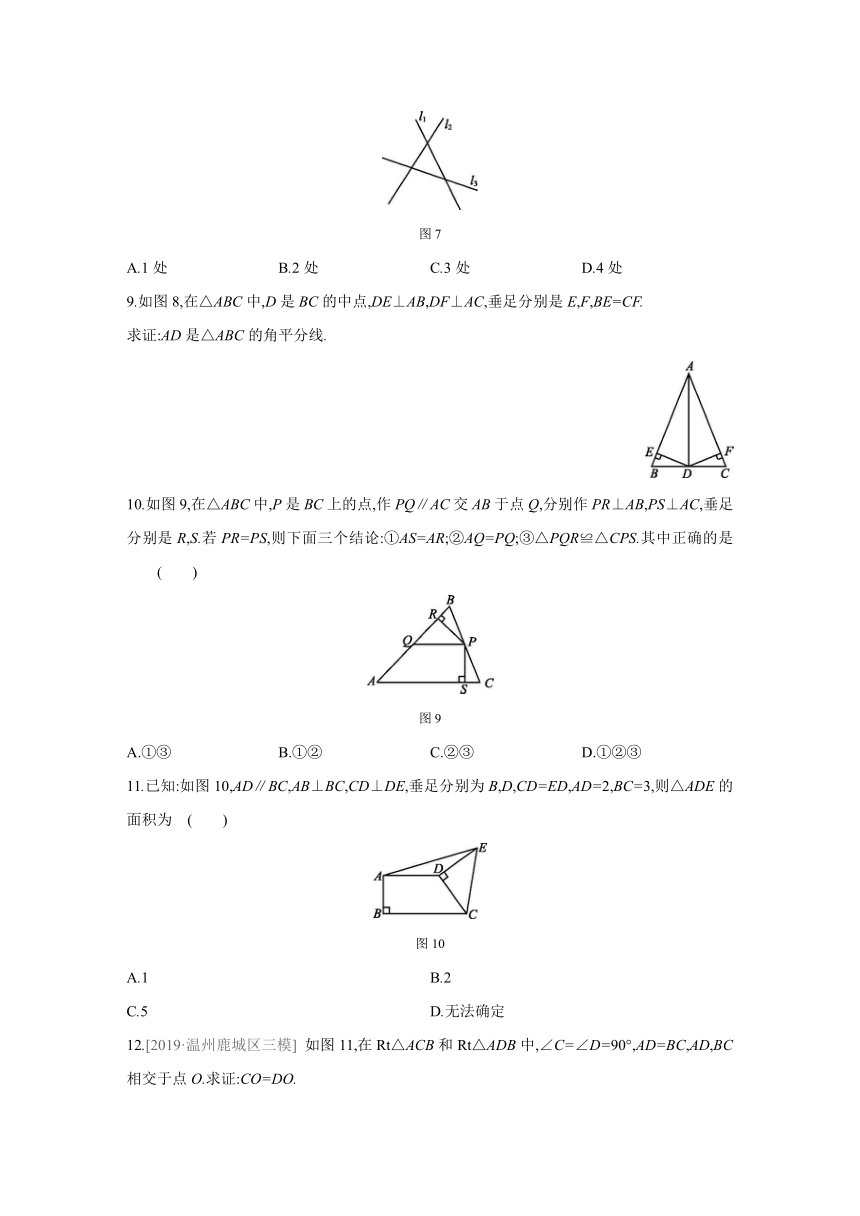
8.如图7,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有 ( )
图7
A.1处 B.2处 C.3处 D.4处
9.如图8,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
求证:AD是△ABC的角平分线.
10.如图9,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S.若PR=PS,则下面三个结论:①AS=AR;②AQ=PQ;③△PQR≌△CPS.其中正确的是 ( )
图9
A.①③ B.①② C.②③ D.①②③
11.已知:如图10,AD∥BC,AB⊥BC,CD⊥DE,垂足分别为B,D,CD=ED,AD=2,BC=3,则△ADE的面积为 ( )
图10
A.1 B.2
C.5 D.无法确定
12.[2019·温州鹿城区三模] 如图11,在Rt△ACB和Rt△ADB中,∠C=∠D=90°,AD=BC,AD,BC相交于点O.求证:CO=DO.
图11
13.如图12,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BD=DF.
求证:(1)CF=EB;
(2)AB=AF+2EB.
图12
14.如图13所示,已知P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足分别为C,D,连结CD.
(1)∠PCD=∠PDC吗?为什么?
(2)OP垂直平分线段CD吗?为什么?
15.如图14①,A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,垂足分别为E,F,且AB=CD.
(1)求证:BD平分EF;
(2)若将△DEC的边EC沿AC方向移动变为图②,其余的条件不变,上述结论是否成立?请说明理由.
图14
教师详解详析
1.A
2.D [解析] 当相等的边在一个三角形中是直角边,在另一个三角形中是斜边时,两直角三角形就不全等了.故选D.
3.B [解析] 在Rt△ABC和Rt△ADC中,
∵CB=CD,AC=AC,
∴Rt△ABC≌Rt△ADC(HL),
∴∠2=∠ACB=90°-∠1=50°.
4.AC=BD(或AD=BC)
5.已知 90 CD HL 全等三角形的对应角相等 在同一个三角形中,等角对等边
6.25 [解析] ∵CD⊥OA于点D,CE⊥OB于点E,
∴CD=CE,
∴OC平分∠AOB.
∵∠AOB=50°,
∴∠DOC=12∠AOB=25°.
故答案为25.
7.D
8.D [解析] 满足条件的有:
(1)三角形两个内角平分线的交点,共1处;
(2)三个外角两两平分线的交点,共3处.
9.证明:∵DE⊥AB,DF⊥AC,
∴△BDE和△CDF是直角三角形.
在Rt△BDE和Rt△CDF中,
∵BD=CD,BE=CF,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
10.B [解析] 如图,连结AP.∵PR=PS,PR⊥AB,垂足为R,PS⊥AC,垂足为S,
∴∠ARP=∠ASP=90°,
AP是∠BAC的平分线,
∴∠1=∠2,
∴△APR≌△APS,
∴AS=AR,
故①正确;
∵QP∥AC,
∴∠2=∠3.
又∠1=∠2,
∴∠1=∠3,
∴AQ=PQ,故②正确;
没有办法证明△PQR≌△CPS,故③不正确.
故选B.
11.A [解析] 如图,过点D作DG⊥BC于点G,过点E作EF⊥AD交AD的延长线于点F.
∵∠EDF+∠FDC=90°,∠CDG+∠FDC=90°,∴∠EDF=∠CDG.
又∵CD=ED,∠DGC=∠DFE=90°,∴△DGC≌△DFE(AAS),
∴EF=CG=3-2=1,
∴S△ADE=12AD·EF=12×2×1=1.
故选A.
12.证明:在Rt△ACB和Rt△BDA中,
∵BC=AD,AB=BA,
∴Rt△ACB≌Rt△BDA(HL),
∴∠CBA=∠DAB,
∴OA=OB.
又AD=BC,
∴CO=DO.
13.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴DE=DC.
在Rt△CDF和Rt△EDB中,DF=DB,DC=DE,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)在Rt△ADC和Rt△ADE中,
∵DC=DE,AD=AD,
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE.
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
14.解:(1)∠PCD=∠PDC.
理由:∵OP是∠AOB的平分线,
且PC⊥OA,PD⊥OB,
∴PC=PD,∴∠PCD=∠PDC.
(2)OP垂直平分线段CD.
理由:∵PC⊥OA,PD⊥OB,
∴∠OCP=∠ODP=90°.
在Rt△POC和Rt△POD中,∵PC=PD,OP=OP,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD.
由PC=PD,OC=OD,可知O,P都是线段CD的垂直平分线上的点,
∴OP垂直平分线段CD.
15.解:(1)证明:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
∵AE=CF,∴AF=CE.
在Rt△ABF和Rt△CDE中,∵AB=CD,AF=CE,
∴Rt△ABF≌Rt△CDE(HL),∴BF=DE.
在△GDE和△GBF中,
∵∠EGD=∠FGB,∠DEG=∠BFG=90°,DE=BF,
∴△GDE≌△GBF(AAS),
∴EG=FG,即BD平分EF.
(2)结论仍成立.理由如下:
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
∵AE=CF,∴AF=CE.
在Rt△ABF和Rt△CDE中,
∵AB=CD,AF=CE,
∴Rt△ABF≌Rt△CDE(HL),∴BF=DE.
在△GDE和△GBF中,
∵∠EGD=∠FGB,∠DEG=∠BFG=90°,DE=BF,
∴△GDE≌△GBF(AAS),
∴EG=FG,即BD平分EF.
知识点1 “HL”定理
1.如图1,∠BAD=∠BCD=90°,AB=CB,可以证明△BAD≌△BCD的理由是 ( )
图1
A.HL B.ASA
C.SAS D.AAS
2.[2017·杭州余杭区月考] 下列条件中,不能判定两个直角三角形全等的是 ( )
A.一锐角和斜边对应相等
B.两条直角边对应相等
C.斜边和一直角边对应相等
D.任意一角和一边分别相等
3.如图2,∠B=∠D=90°,CB=CD,∠1=40°,则∠2的度数为 ( )
图2
A.40° B.50° C.60° D.75°
4.[2019·台州期中] 如图3,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”直接判定Rt△ABC≌Rt△BAD,则你添加的条件是 .?
图3
5.已知:如图4,在△ABC中,D是BC的中点,DE⊥AB于点E,DF⊥AC于点F,且BE=CF.求证:AB=AC.
图4
完成下面的证明过程.
证明:∵DE⊥AB,DF⊥AC( ),?
∴∠BED=∠CFD= °.?
∵D是BC的中点,
∴BD= .?
又∵BE=CF,
∴Rt△BDE≌Rt△CDF( ),?
∴∠B=∠C( ),?
∴AB=AC( ).?
知识点2 角平分线性质定理的逆定理
6.[2019·衢州期中] 如图5,∠AOB=50°,CD⊥OA于点D,CE⊥OB于点E,且CD=CE,则∠DOC= °.?
图5
7.已知:如图6,OC是∠AOB内部的一条射线,P是射线OC上任意一点,PD⊥OA,PE⊥OB,垂足分别为D,E.有下列条件:①∠AOC=∠BOC;②PD=PE;③OD=OE;④∠DPO=∠EPO.其中,能判定OC是∠AOB的平分线的有 ( )
图6
A.1个 B.2个 C.3个 D.4个
8.如图7,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有 ( )
图7
A.1处 B.2处 C.3处 D.4处
9.如图8,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
求证:AD是△ABC的角平分线.
10.如图9,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S.若PR=PS,则下面三个结论:①AS=AR;②AQ=PQ;③△PQR≌△CPS.其中正确的是 ( )
图9
A.①③ B.①② C.②③ D.①②③
11.已知:如图10,AD∥BC,AB⊥BC,CD⊥DE,垂足分别为B,D,CD=ED,AD=2,BC=3,则△ADE的面积为 ( )
图10
A.1 B.2
C.5 D.无法确定
12.[2019·温州鹿城区三模] 如图11,在Rt△ACB和Rt△ADB中,∠C=∠D=90°,AD=BC,AD,BC相交于点O.求证:CO=DO.
图11
13.如图12,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BD=DF.
求证:(1)CF=EB;
(2)AB=AF+2EB.
图12
14.如图13所示,已知P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足分别为C,D,连结CD.
(1)∠PCD=∠PDC吗?为什么?
(2)OP垂直平分线段CD吗?为什么?
15.如图14①,A,E,F,C在同一条直线上,AE=CF,过点E,F分别作DE⊥AC,BF⊥AC,垂足分别为E,F,且AB=CD.
(1)求证:BD平分EF;
(2)若将△DEC的边EC沿AC方向移动变为图②,其余的条件不变,上述结论是否成立?请说明理由.
图14
教师详解详析
1.A
2.D [解析] 当相等的边在一个三角形中是直角边,在另一个三角形中是斜边时,两直角三角形就不全等了.故选D.
3.B [解析] 在Rt△ABC和Rt△ADC中,
∵CB=CD,AC=AC,
∴Rt△ABC≌Rt△ADC(HL),
∴∠2=∠ACB=90°-∠1=50°.
4.AC=BD(或AD=BC)
5.已知 90 CD HL 全等三角形的对应角相等 在同一个三角形中,等角对等边
6.25 [解析] ∵CD⊥OA于点D,CE⊥OB于点E,
∴CD=CE,
∴OC平分∠AOB.
∵∠AOB=50°,
∴∠DOC=12∠AOB=25°.
故答案为25.
7.D
8.D [解析] 满足条件的有:
(1)三角形两个内角平分线的交点,共1处;
(2)三个外角两两平分线的交点,共3处.
9.证明:∵DE⊥AB,DF⊥AC,
∴△BDE和△CDF是直角三角形.
在Rt△BDE和Rt△CDF中,
∵BD=CD,BE=CF,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.
10.B [解析] 如图,连结AP.∵PR=PS,PR⊥AB,垂足为R,PS⊥AC,垂足为S,
∴∠ARP=∠ASP=90°,
AP是∠BAC的平分线,
∴∠1=∠2,
∴△APR≌△APS,
∴AS=AR,
故①正确;
∵QP∥AC,
∴∠2=∠3.
又∠1=∠2,
∴∠1=∠3,
∴AQ=PQ,故②正确;
没有办法证明△PQR≌△CPS,故③不正确.
故选B.
11.A [解析] 如图,过点D作DG⊥BC于点G,过点E作EF⊥AD交AD的延长线于点F.
∵∠EDF+∠FDC=90°,∠CDG+∠FDC=90°,∴∠EDF=∠CDG.
又∵CD=ED,∠DGC=∠DFE=90°,∴△DGC≌△DFE(AAS),
∴EF=CG=3-2=1,
∴S△ADE=12AD·EF=12×2×1=1.
故选A.
12.证明:在Rt△ACB和Rt△BDA中,
∵BC=AD,AB=BA,
∴Rt△ACB≌Rt△BDA(HL),
∴∠CBA=∠DAB,
∴OA=OB.
又AD=BC,
∴CO=DO.
13.证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴DE=DC.
在Rt△CDF和Rt△EDB中,DF=DB,DC=DE,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)在Rt△ADC和Rt△ADE中,
∵DC=DE,AD=AD,
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE.
∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
14.解:(1)∠PCD=∠PDC.
理由:∵OP是∠AOB的平分线,
且PC⊥OA,PD⊥OB,
∴PC=PD,∴∠PCD=∠PDC.
(2)OP垂直平分线段CD.
理由:∵PC⊥OA,PD⊥OB,
∴∠OCP=∠ODP=90°.
在Rt△POC和Rt△POD中,∵PC=PD,OP=OP,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD.
由PC=PD,OC=OD,可知O,P都是线段CD的垂直平分线上的点,
∴OP垂直平分线段CD.
15.解:(1)证明:∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
∵AE=CF,∴AF=CE.
在Rt△ABF和Rt△CDE中,∵AB=CD,AF=CE,
∴Rt△ABF≌Rt△CDE(HL),∴BF=DE.
在△GDE和△GBF中,
∵∠EGD=∠FGB,∠DEG=∠BFG=90°,DE=BF,
∴△GDE≌△GBF(AAS),
∴EG=FG,即BD平分EF.
(2)结论仍成立.理由如下:
∵DE⊥AC,BF⊥AC,
∴∠BFA=∠DEC=90°.
∵AE=CF,∴AF=CE.
在Rt△ABF和Rt△CDE中,
∵AB=CD,AF=CE,
∴Rt△ABF≌Rt△CDE(HL),∴BF=DE.
在△GDE和△GBF中,
∵∠EGD=∠FGB,∠DEG=∠BFG=90°,DE=BF,
∴△GDE≌△GBF(AAS),
∴EG=FG,即BD平分EF.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
