5.5 一次函数的简单应用(2课时)---同步课时作业 2021-2022学年浙教版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 5.5 一次函数的简单应用(2课时)---同步课时作业 2021-2022学年浙教版数学八年级上册(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 239.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-28 00:00:00 | ||
图片预览




文档简介
5.5 一次函数的简单应用
第1课时 判定一次函数关系及其应用
知识点1 建立一次函数模型
1.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内剩余油量Q(升)与行驶时间t(时)之间的函数表达式为 ( )
A.Q=5t B.Q=5t+40
C.Q=40-5t(0≤t≤8) D.以上答案都不对
2.皮球从高处落下时,弹跳高度b(cm)与下落高度d(cm)的关系如下表所示,求b与d之间的函数表达式.
下落高度d(cm)
…
80
100
150
…
弹跳高度b(cm)
…
40
50
75
…
3.一盘蚊香长105 cm,点燃后每小时缩短10 cm.
(1)请写出点燃后蚊香的长度y(cm)与蚊香燃烧时间t(h)之间的函数表达式;
(2)该蚊香可点燃多长时间?
知识点2 实际问题中的分段函数
4.汽车以60千米/时的速度在公路上匀速行驶,1小时后进入高速路,继续以100千米/时的速度匀速行驶,则汽车行驶的路程s(千米)与行驶的时间t(时)的函数图象大致是 ( )
图1
5.周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选了一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图2描述了小丽路上的情景,下列说法中错误的是 ( )
图2
A.小丽从家到达公园共用时20分钟
B.公园离小丽家的距离为2000米
C.小丽在便利店的时间为15分钟
D.便利店离小丽家的距离为1000米
6.如图3,小明购买一种笔记本所付金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8本笔记本比分8次购买每次购买1本可节省 元.?
图3
7.某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价2元收费;若每月用水量超过14吨,则超过部分每吨按市场价3.5元收费.
(1)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数表达式;
(2)小明家5月份用水30吨,则他家5月份应交水费多少元?
8.[2019·温岭期末] 五一小长假,李军与张明相约去宁波旅游,李军从温岭北上沿海高速,同时张明从玉环芦浦上沿海高速,温岭北与玉环芦浦相距44千米,两人约好在三门服务区集合,李军由于离三门服务区近,行驶了1.2小时先到达三门服务区等候张明,张明走了1.4小时到达三门服务区.在整个过程中,两人均保持各自的速度匀速行驶,两人相距的路程y(千米)与张明行驶的时间x(时)的关系如图4所示,下列说法错误的是 ( )
图4
A.李军的速度是80千米/时
B.张明的速度是100千米/时
C.玉环芦浦至三门服务区的路程是140千米
D.温岭北至三门服务区的路程是44千米
9.[2019·绍兴] 如图5是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象.
(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程;当0≤x≤150时,求1千瓦时的电量汽车能行驶的路程;
(2)当150≤x≤200时,求y关于x的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
图5
10.[2019·温州] 某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人;
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
5.5 一次函数的简单应用
第2课时 两个一次函数的应用
知识点1 一次函数与二元一次方程组的关系
1.[2019·温州苍南县一模] 一次函数y1=x+1与y2=-2x+4的图象交点的横坐标是 ( )
A.4 B.2 C.1 D.0
2.若二元一次方程组4x-y=1,y=2x-m的解是x=2,y=7,则一次函数y=2x-m的图象与一次函数y=4x-1的图象的交点坐标为 .?
3.[教材课内练习第1题变式] 用图象法解二元一次方程组2x+y=4,2x-3y=12.
知识点2 一次函数与不等式的关系
4.如图6所示的是函数y=kx+b(k,b为常数,k≠0)的图象,则关于x的不等式kx+b<0的解为 ( )
图6
A.x>0 B.x<0 C.x<2 D.x>2
5.[2019·温岭一模] 如图7,直线y=x+b与直线y=kx+6交于点P(1,3),则关于x的不等式x+b>kx+6的解是 ( )
图7
A.x<1 B.x>1 C.x>3 D.x<3
知识点3 两个一次函数的应用
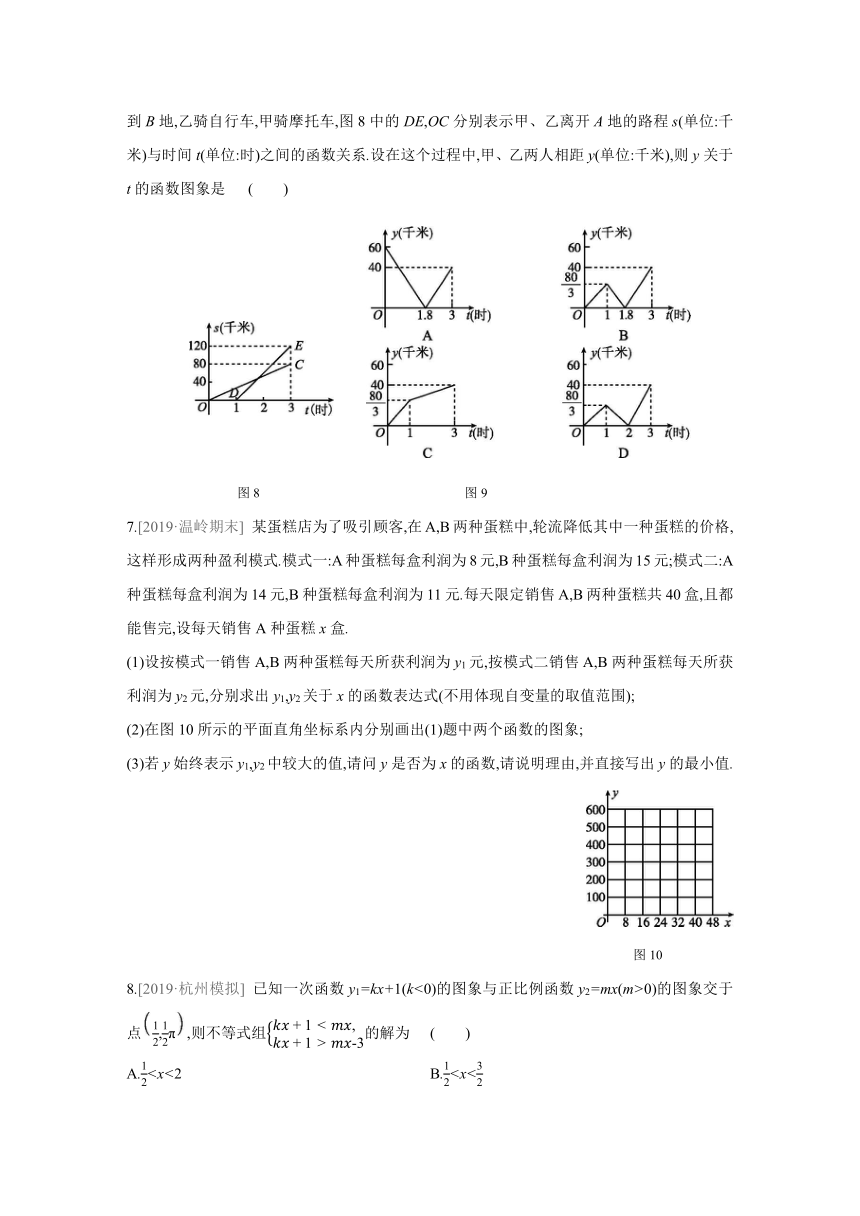
6.[2019·杭州萧山区模拟] 已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图8中的DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:时)之间的函数关系.设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是 ( )
2106930180975
554355127635
图8 图9
7.[2019·温岭期末] 某蛋糕店为了吸引顾客,在A,B两种蛋糕中,轮流降低其中一种蛋糕的价格,这样形成两种盈利模式.模式一:A种蛋糕每盒利润为8元,B种蛋糕每盒利润为15元;模式二:A种蛋糕每盒利润为14元,B种蛋糕每盒利润为11元.每天限定销售A,B两种蛋糕共40盒,且都能售完,设每天销售A种蛋糕x盒.
(1)设按模式一销售A,B两种蛋糕每天所获利润为y1元,按模式二销售A,B两种蛋糕每天所获利润为y2元,分别求出y1,y2关于x的函数表达式(不用体现自变量的取值范围);
(2)在图10所示的平面直角坐标系内分别画出(1)题中两个函数的图象;
(3)若y始终表示y1,y2中较大的值,请问y是否为x的函数,请说明理由,并直接写出y的最小值.
图10
8.[2019·杭州模拟] 已知一次函数y1=kx+1(k<0)的图象与正比例函数y2=mx(m>0)的图象交于点12,12π,则不等式组kx+1mx-3的解为 ( )
A.12C.x>12 D.09.若把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是 ( )
A.1C.m>1 D.m<4
10.[2019·温岭期末] 已知方程组y=kx-b,y=?x+a的解是x=?1,y=3,则直线y=-kx+b与直线y=x-a的交点坐标是 .?
11.[2019·台州天台县期末] 在平面直角坐标系xOy中,直线y=32x+b与直线y=12x交于点A(m,1),且与y轴交于点B.
(1)求m的值和点B的坐标;
(2)若点C在y轴上,且△ABC的面积是1,请直接写出点C的坐标.
12.[2019·宁波] 某风景区内的公路如图11①所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程y(米)与小聪出发的时间x(分)之间的函数关系如图11②所示.
(1)求第一班车离入口处的路程y(米)与小聪出发的时间x(分)的函数表达式;
(2)求第一班车从入口处到达塔林所需的时间;
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
教师详解详析
1.C [解析] 依题意,得油箱内剩余油量Q(升)与行驶时间t(时)之间的函数表达式为Q=40-5t(0≤t≤8).
故选C.
2.解:设弹跳高度b(cm)与下落高度d(cm)之间的函数表达式为b=kd(k≠0).
由表知40=80k,解得k=12.∴b=d2.
即b与d之间的函数表达式为b=d2.
3.解:(1)∵蚊香的长度等于蚊香的原长减去燃烧的长度,
∴y=105-10t(0≤t≤10.5).
(2)∵蚊香燃尽的时候蚊香的长度y=0,
∴105-10t=0,
解得t=10.5.
∴该蚊香可点燃10.5 h.
4.C [解析] 由题意知,前1小时路程随时间增大而增大,1小时后路程的增加幅度会变大一点.故选C.
5.C
6.4 [解析] 由线段OB可知1本笔记本的价钱为5元.
设射线BE的函数表达式为y=kx+b(k≠0,x≥4).
把(4,20),(10,44)代入,得
20=4k+b,44=10k+b,解得k=4,b=4,
∴射线BE的函数表达式为y=4x+4(x≥4).
当x=8时,y=4×8+4=36.
∵5×8-36=4(元).故答案为4.
7.解:(1)由题意,得
当0≤x≤14时,y=2x;
当x>14时,y=2×14+(x-14)×3.5=3.5x-21.
综上,y与x的函数表达式为
y=2x(0≤x≤14),3.5x-21(x>14).
(2)当x=30时,y=3.5×30-21=84.
即小明家5月份用水30吨,则他家应交水费84元.
8.D [解析] 李军的速度为20÷(1.4-1.2)-(44-20)÷1.2=80(千米/时),故选项A不合题意;张明的速度为20÷(1.4-1.2)=100(千米/时),故选项B不合题意;玉环芦浦至三门服务站的路程为100×1.4=140(千米),故选项C不合题意;温岭北至三门服务站的路程为80×1.2=96(千米),故选项D符合题意.
故选D.
9.解:(1)由图象可知,蓄电池剩余电量为35千瓦时时汽车已行驶了150千米.
当0≤x≤150时,1千瓦时的电量汽车能行驶的路程为15060-35=6(千米).
(2)设y=kx+b(k≠0).
把点(150,35),(200,10)代入,
得150k+b=35,200k+b=10,解得k=-0.5,b=110.
∴y=-0.5x+110.
当x=180时,y=-0.5×180+110=20.
答:当150≤x≤200时,函数表达式为y=-0.5x+110.当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时.
10.解:(1)设成人有x人,少年有y人.
根据题意,得x+y+10=32,x=y+12,解得x=17,y=5.
答:该旅行团中成人与少年分别是17人、5人.
(2)①由成人8人和少年5人带队时,所需门票的总费用是100×8+5×100×0.8+(10-8)×100×0.6=1320(元).
答:由成人8人和少年5人带队,所需门票的总费用是1320元.
②设可以安排成人a人,少年b人带队,
则1≤a≤17,1≤b≤5.
当10≤a≤17时,
若a=10,则费用为100×10+100×b×0.8≤1200,解得b≤2.5.
∴b的最大值是2,此时a+b=12,费用为1160元;
若a=11,则费用为100×11+100×b×0.8≤1200,解得b≤54.
∴b的最大值是1,此时a+b=12,费用为1180元;
若a≥12,则100a≥1200,即成人门票的费用至少是1200元,不合题意,舍去;
当1≤a<10时,
若a=9,则费用为100×9+100b×0.8+100×1×0.6≤1200,解得b≤3.
∴b的最大值是3,此时a+b=12,费用为1200元;
若a=8,则费用为100×8+100b×0.8+100×2×0.6≤1200,解得b≤3.5.
∴b的最大值是3,a+b=11<12,不合题意,舍去;
同理,当a<8时,a+b<12,不合题意,舍去.
综上所述,最多安排成人和少年共12人带队,有三种方案,分别是:成人10人,少年2人;成人11人,少年1人;成人9人,少年3人.其中成人10人,少年2人时购票费用最少.
教师详解详析
1.C [解析] 根据题意,可得x+1=-2x+4,解得x=1.故选C.
2.(2,7) [解析] ∵二元一次方程组4x-y=1,y=2x-m的解是x=2,y=7,
∴一次函数y=2x-m的图象与一次函数y=4x-1的图象的交点坐标为(2,7).
故答案为(2,7).
3.解:在同一个平面直角坐标系中分别画出一次函数y=-2x+4与y=23x-4的图象,如图所示:
观察图象,知两直线的交点坐标为(3,-2).
故二元一次方程组2x+y=4,2x-3y=12的解为x=3,y=-2.
4.D [解析] 函数y=kx+b的图象经过点(2,0),并且函数值y随x的增大而减小,
所以当x>2时,函数值小于0,即关于x的不等式kx+b<0的解是x>2.故选D.
5.B [解析] 当x>1时,x+b>kx+6,
即不等式x+b>kx+6的解为x>1.
故选B.
6.B [解析] 由题意和图象,得乙到达B地时甲距A地120 km,开始时两人的距离为0;
甲的速度是120÷(3-1)=60(km/h),乙的速度是80÷3=803(km/h),即乙出发1 h后两人距离为803 km.
设乙出发后被甲追上的时间为x h,则60(x-1)=803x,解得x=1.8,即乙出发后被甲追上的时间为1.8 h.
所以符合题意的函数图象只有选项B.
故选B.
7.解:(1)由题意得y1=8x+15(40-x),y2=14x+11(40-x),
即y1=-7x+600,y2=3x+440.
(2)略
(3)y是x的函数.理由如下:
令y1=y2,则x=16.
∵当0≤x≤40时,y1随着x的增大而减小,y2随着x的增大而增大,
∴y=-7x+600(0≤x≤16),3x+440(16∵每一个自变量x均有唯一一个y值与之对应,
∴y为x的函数.
当x=16时,y有最小值,y的最小值为488.
8.A [解析] ∵一次函数y1=kx+1(k<0)与正比例函数y2=mx(m>0)的图象均过点12,12π,
∴12π=12k+1,12π=12m,
∴12m=12k+1,解得m=k+2.
∴不等式组kx+1mx-3
即为kx+1<(k+2)x,kx+1>(k+2)x-3,解得129.C
10.(-1,-3) [解析] ∵方程组y=kx-b,y=-x+a的解是x=-1,y=3,
∴直线y=kx-b与直线y=-x+a的交点坐标为(-1,3),
∴直线y=-kx+b与直线y=x-a的交点坐标是(-1,-3).故答案为(-1,-3).
11.解:(1)∵直线y=32x+b与直线y=12x交于点A(m,1),
∴12m=1,解得m=2.∴A(2,1).
将A(2,1)代入y=32x+b,可得32×2+b=1,
解得b=-2.∴B(0,-2).
(2)点C(0,-1)或C(0,-3).
12.解:(1)设第一班车离入口处的路程y与小聪出发的时间x的函数表达式为y=kx+b(k≠0).
把(20,0),(38,2700)代入y=kx+b,
得0=20k+b,2700=38k+b,解得k=150,b=-3000.
∴第一班车离入口处的路程y(米)与小聪出发的时间x(分)的函数表达式为y=150x-3000(20≤x≤38).
(2)把y=1500代入y=150x-3000,
解得x=30.
30-20=10(分).
∴第一班车从入口处到达塔林所需时间为10分钟.
(3)设小聪坐上了第n班车,则
30-25+10(n-1)≥40,解得n≥4.5.
∴小聪最早坐上第5班车.
等车的时间为5分钟,坐班车所需时间为1200÷150=8(分);
步行所需时间为1200÷(1500÷25)=20(分).
20-(8+5)=7(分).
∴如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早7分钟.
第1课时 判定一次函数关系及其应用
知识点1 建立一次函数模型
1.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内剩余油量Q(升)与行驶时间t(时)之间的函数表达式为 ( )
A.Q=5t B.Q=5t+40
C.Q=40-5t(0≤t≤8) D.以上答案都不对
2.皮球从高处落下时,弹跳高度b(cm)与下落高度d(cm)的关系如下表所示,求b与d之间的函数表达式.
下落高度d(cm)
…
80
100
150
…
弹跳高度b(cm)
…
40
50
75
…
3.一盘蚊香长105 cm,点燃后每小时缩短10 cm.
(1)请写出点燃后蚊香的长度y(cm)与蚊香燃烧时间t(h)之间的函数表达式;
(2)该蚊香可点燃多长时间?
知识点2 实际问题中的分段函数
4.汽车以60千米/时的速度在公路上匀速行驶,1小时后进入高速路,继续以100千米/时的速度匀速行驶,则汽车行驶的路程s(千米)与行驶的时间t(时)的函数图象大致是 ( )
图1
5.周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选了一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图2描述了小丽路上的情景,下列说法中错误的是 ( )
图2
A.小丽从家到达公园共用时20分钟
B.公园离小丽家的距离为2000米
C.小丽在便利店的时间为15分钟
D.便利店离小丽家的距离为1000米
6.如图3,小明购买一种笔记本所付金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8本笔记本比分8次购买每次购买1本可节省 元.?
图3
7.某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价2元收费;若每月用水量超过14吨,则超过部分每吨按市场价3.5元收费.
(1)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数表达式;
(2)小明家5月份用水30吨,则他家5月份应交水费多少元?
8.[2019·温岭期末] 五一小长假,李军与张明相约去宁波旅游,李军从温岭北上沿海高速,同时张明从玉环芦浦上沿海高速,温岭北与玉环芦浦相距44千米,两人约好在三门服务区集合,李军由于离三门服务区近,行驶了1.2小时先到达三门服务区等候张明,张明走了1.4小时到达三门服务区.在整个过程中,两人均保持各自的速度匀速行驶,两人相距的路程y(千米)与张明行驶的时间x(时)的关系如图4所示,下列说法错误的是 ( )
图4
A.李军的速度是80千米/时
B.张明的速度是100千米/时
C.玉环芦浦至三门服务区的路程是140千米
D.温岭北至三门服务区的路程是44千米
9.[2019·绍兴] 如图5是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象.
(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程;当0≤x≤150时,求1千瓦时的电量汽车能行驶的路程;
(2)当150≤x≤200时,求y关于x的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
图5
10.[2019·温州] 某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人;
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
5.5 一次函数的简单应用
第2课时 两个一次函数的应用
知识点1 一次函数与二元一次方程组的关系
1.[2019·温州苍南县一模] 一次函数y1=x+1与y2=-2x+4的图象交点的横坐标是 ( )
A.4 B.2 C.1 D.0
2.若二元一次方程组4x-y=1,y=2x-m的解是x=2,y=7,则一次函数y=2x-m的图象与一次函数y=4x-1的图象的交点坐标为 .?
3.[教材课内练习第1题变式] 用图象法解二元一次方程组2x+y=4,2x-3y=12.
知识点2 一次函数与不等式的关系
4.如图6所示的是函数y=kx+b(k,b为常数,k≠0)的图象,则关于x的不等式kx+b<0的解为 ( )
图6
A.x>0 B.x<0 C.x<2 D.x>2
5.[2019·温岭一模] 如图7,直线y=x+b与直线y=kx+6交于点P(1,3),则关于x的不等式x+b>kx+6的解是 ( )
图7
A.x<1 B.x>1 C.x>3 D.x<3
知识点3 两个一次函数的应用
6.[2019·杭州萧山区模拟] 已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图8中的DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:时)之间的函数关系.设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是 ( )
2106930180975
554355127635
图8 图9
7.[2019·温岭期末] 某蛋糕店为了吸引顾客,在A,B两种蛋糕中,轮流降低其中一种蛋糕的价格,这样形成两种盈利模式.模式一:A种蛋糕每盒利润为8元,B种蛋糕每盒利润为15元;模式二:A种蛋糕每盒利润为14元,B种蛋糕每盒利润为11元.每天限定销售A,B两种蛋糕共40盒,且都能售完,设每天销售A种蛋糕x盒.
(1)设按模式一销售A,B两种蛋糕每天所获利润为y1元,按模式二销售A,B两种蛋糕每天所获利润为y2元,分别求出y1,y2关于x的函数表达式(不用体现自变量的取值范围);
(2)在图10所示的平面直角坐标系内分别画出(1)题中两个函数的图象;
(3)若y始终表示y1,y2中较大的值,请问y是否为x的函数,请说明理由,并直接写出y的最小值.
图10
8.[2019·杭州模拟] 已知一次函数y1=kx+1(k<0)的图象与正比例函数y2=mx(m>0)的图象交于点12,12π,则不等式组kx+1
A.12
A.1
10.[2019·温岭期末] 已知方程组y=kx-b,y=?x+a的解是x=?1,y=3,则直线y=-kx+b与直线y=x-a的交点坐标是 .?
11.[2019·台州天台县期末] 在平面直角坐标系xOy中,直线y=32x+b与直线y=12x交于点A(m,1),且与y轴交于点B.
(1)求m的值和点B的坐标;
(2)若点C在y轴上,且△ABC的面积是1,请直接写出点C的坐标.
12.[2019·宁波] 某风景区内的公路如图11①所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程y(米)与小聪出发的时间x(分)之间的函数关系如图11②所示.
(1)求第一班车离入口处的路程y(米)与小聪出发的时间x(分)的函数表达式;
(2)求第一班车从入口处到达塔林所需的时间;
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
教师详解详析
1.C [解析] 依题意,得油箱内剩余油量Q(升)与行驶时间t(时)之间的函数表达式为Q=40-5t(0≤t≤8).
故选C.
2.解:设弹跳高度b(cm)与下落高度d(cm)之间的函数表达式为b=kd(k≠0).
由表知40=80k,解得k=12.∴b=d2.
即b与d之间的函数表达式为b=d2.
3.解:(1)∵蚊香的长度等于蚊香的原长减去燃烧的长度,
∴y=105-10t(0≤t≤10.5).
(2)∵蚊香燃尽的时候蚊香的长度y=0,
∴105-10t=0,
解得t=10.5.
∴该蚊香可点燃10.5 h.
4.C [解析] 由题意知,前1小时路程随时间增大而增大,1小时后路程的增加幅度会变大一点.故选C.
5.C
6.4 [解析] 由线段OB可知1本笔记本的价钱为5元.
设射线BE的函数表达式为y=kx+b(k≠0,x≥4).
把(4,20),(10,44)代入,得
20=4k+b,44=10k+b,解得k=4,b=4,
∴射线BE的函数表达式为y=4x+4(x≥4).
当x=8时,y=4×8+4=36.
∵5×8-36=4(元).故答案为4.
7.解:(1)由题意,得
当0≤x≤14时,y=2x;
当x>14时,y=2×14+(x-14)×3.5=3.5x-21.
综上,y与x的函数表达式为
y=2x(0≤x≤14),3.5x-21(x>14).
(2)当x=30时,y=3.5×30-21=84.
即小明家5月份用水30吨,则他家应交水费84元.
8.D [解析] 李军的速度为20÷(1.4-1.2)-(44-20)÷1.2=80(千米/时),故选项A不合题意;张明的速度为20÷(1.4-1.2)=100(千米/时),故选项B不合题意;玉环芦浦至三门服务站的路程为100×1.4=140(千米),故选项C不合题意;温岭北至三门服务站的路程为80×1.2=96(千米),故选项D符合题意.
故选D.
9.解:(1)由图象可知,蓄电池剩余电量为35千瓦时时汽车已行驶了150千米.
当0≤x≤150时,1千瓦时的电量汽车能行驶的路程为15060-35=6(千米).
(2)设y=kx+b(k≠0).
把点(150,35),(200,10)代入,
得150k+b=35,200k+b=10,解得k=-0.5,b=110.
∴y=-0.5x+110.
当x=180时,y=-0.5×180+110=20.
答:当150≤x≤200时,函数表达式为y=-0.5x+110.当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时.
10.解:(1)设成人有x人,少年有y人.
根据题意,得x+y+10=32,x=y+12,解得x=17,y=5.
答:该旅行团中成人与少年分别是17人、5人.
(2)①由成人8人和少年5人带队时,所需门票的总费用是100×8+5×100×0.8+(10-8)×100×0.6=1320(元).
答:由成人8人和少年5人带队,所需门票的总费用是1320元.
②设可以安排成人a人,少年b人带队,
则1≤a≤17,1≤b≤5.
当10≤a≤17时,
若a=10,则费用为100×10+100×b×0.8≤1200,解得b≤2.5.
∴b的最大值是2,此时a+b=12,费用为1160元;
若a=11,则费用为100×11+100×b×0.8≤1200,解得b≤54.
∴b的最大值是1,此时a+b=12,费用为1180元;
若a≥12,则100a≥1200,即成人门票的费用至少是1200元,不合题意,舍去;
当1≤a<10时,
若a=9,则费用为100×9+100b×0.8+100×1×0.6≤1200,解得b≤3.
∴b的最大值是3,此时a+b=12,费用为1200元;
若a=8,则费用为100×8+100b×0.8+100×2×0.6≤1200,解得b≤3.5.
∴b的最大值是3,a+b=11<12,不合题意,舍去;
同理,当a<8时,a+b<12,不合题意,舍去.
综上所述,最多安排成人和少年共12人带队,有三种方案,分别是:成人10人,少年2人;成人11人,少年1人;成人9人,少年3人.其中成人10人,少年2人时购票费用最少.
教师详解详析
1.C [解析] 根据题意,可得x+1=-2x+4,解得x=1.故选C.
2.(2,7) [解析] ∵二元一次方程组4x-y=1,y=2x-m的解是x=2,y=7,
∴一次函数y=2x-m的图象与一次函数y=4x-1的图象的交点坐标为(2,7).
故答案为(2,7).
3.解:在同一个平面直角坐标系中分别画出一次函数y=-2x+4与y=23x-4的图象,如图所示:
观察图象,知两直线的交点坐标为(3,-2).
故二元一次方程组2x+y=4,2x-3y=12的解为x=3,y=-2.
4.D [解析] 函数y=kx+b的图象经过点(2,0),并且函数值y随x的增大而减小,
所以当x>2时,函数值小于0,即关于x的不等式kx+b<0的解是x>2.故选D.
5.B [解析] 当x>1时,x+b>kx+6,
即不等式x+b>kx+6的解为x>1.
故选B.
6.B [解析] 由题意和图象,得乙到达B地时甲距A地120 km,开始时两人的距离为0;
甲的速度是120÷(3-1)=60(km/h),乙的速度是80÷3=803(km/h),即乙出发1 h后两人距离为803 km.
设乙出发后被甲追上的时间为x h,则60(x-1)=803x,解得x=1.8,即乙出发后被甲追上的时间为1.8 h.
所以符合题意的函数图象只有选项B.
故选B.
7.解:(1)由题意得y1=8x+15(40-x),y2=14x+11(40-x),
即y1=-7x+600,y2=3x+440.
(2)略
(3)y是x的函数.理由如下:
令y1=y2,则x=16.
∵当0≤x≤40时,y1随着x的增大而减小,y2随着x的增大而增大,
∴y=-7x+600(0≤x≤16),3x+440(16
∴y为x的函数.
当x=16时,y有最小值,y的最小值为488.
8.A [解析] ∵一次函数y1=kx+1(k<0)与正比例函数y2=mx(m>0)的图象均过点12,12π,
∴12π=12k+1,12π=12m,
∴12m=12k+1,解得m=k+2.
∴不等式组kx+1
即为kx+1<(k+2)x,kx+1>(k+2)x-3,解得12
10.(-1,-3) [解析] ∵方程组y=kx-b,y=-x+a的解是x=-1,y=3,
∴直线y=kx-b与直线y=-x+a的交点坐标为(-1,3),
∴直线y=-kx+b与直线y=x-a的交点坐标是(-1,-3).故答案为(-1,-3).
11.解:(1)∵直线y=32x+b与直线y=12x交于点A(m,1),
∴12m=1,解得m=2.∴A(2,1).
将A(2,1)代入y=32x+b,可得32×2+b=1,
解得b=-2.∴B(0,-2).
(2)点C(0,-1)或C(0,-3).
12.解:(1)设第一班车离入口处的路程y与小聪出发的时间x的函数表达式为y=kx+b(k≠0).
把(20,0),(38,2700)代入y=kx+b,
得0=20k+b,2700=38k+b,解得k=150,b=-3000.
∴第一班车离入口处的路程y(米)与小聪出发的时间x(分)的函数表达式为y=150x-3000(20≤x≤38).
(2)把y=1500代入y=150x-3000,
解得x=30.
30-20=10(分).
∴第一班车从入口处到达塔林所需时间为10分钟.
(3)设小聪坐上了第n班车,则
30-25+10(n-1)≥40,解得n≥4.5.
∴小聪最早坐上第5班车.
等车的时间为5分钟,坐班车所需时间为1200÷150=8(分);
步行所需时间为1200÷(1500÷25)=20(分).
20-(8+5)=7(分).
∴如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早7分钟.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
