第一章:三角形的初步知识单元测试-2021-2022学年浙教版八年级数学上册测试卷(word版含答案)
文档属性
| 名称 | 第一章:三角形的初步知识单元测试-2021-2022学年浙教版八年级数学上册测试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 272.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-27 00:00:00 | ||
图片预览


文档简介
11417300108204002021-2022学年1089660011620500浙教版八年级数学上册测试卷
第一章:三角形的初步知识单元测试
(时间:100分钟 满分:120分)
一.选择题(每小题3分,共30分)
1.已知AB=1.5,AC=4.5,若BC的长为整数,则BC的长为()
A.3
B.6
C.3或6
D.3或4或5或6
2.一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是()
A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形
3.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为()
A.80°
B.90°
C.100°
D.102°
,第4题图) ,第5题图) ,第6题图)
4.如图,△ABC的平分线AD与中线BE交于点O,有下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线,下列说法正确的是(
)
A.①②都正确B.①不正确,②正确
C.①②都不正确D.①正确,②不正确
5.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为(
)
A.20°
B.30°
C.35°
D.40°
6.要测量河两岸的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,使A,C,E在同一条直线上(如图),可以证明△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长.在这里判定△ABC≌△EDC的条件是(
)
A.ASA
B.SAS
C.SSS
D.以上答案均不正确
7.如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中能使△ABC≌△DEF的条件共有()
A.1组B.2组C.3组D.4组
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是()
A.3
B.4
C.6
D.5
,第7题图) ,第8题图) ,第9题图) ,第10题图)
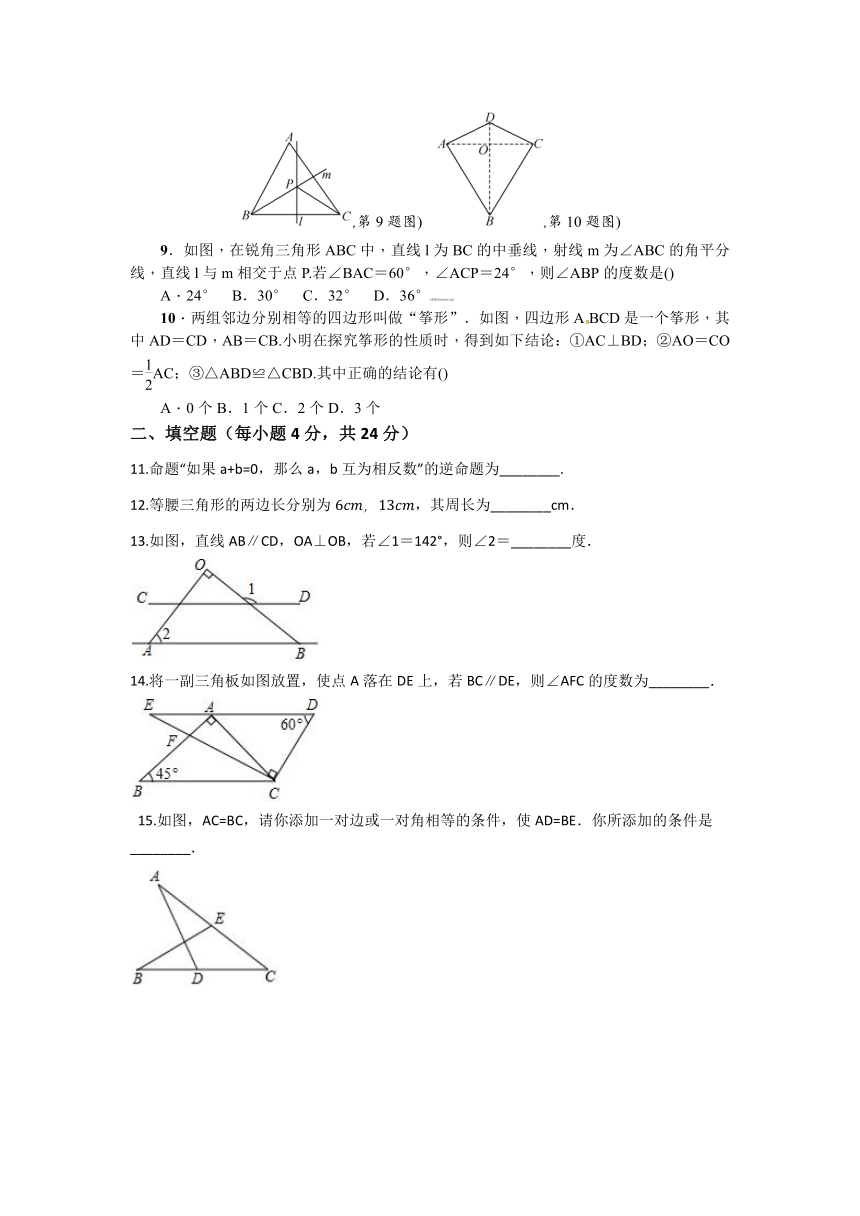
9.如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是()
A.24°
B.30°
C.32°
D.36°[]
10.两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB.小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD.其中正确的结论有()
A.0个B.1个C.2个D.3个
二、填空题(每小题4分,共24分)
11.命题“如果a+b=0,那么a,b互为相反数”的逆命题为________.
12.等腰三角形的两边长分别为6cm,13cm,其周长为________cm.
13.如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=________度.
14.将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为________.
15.如图,AC=BC,请你添加一对边或一对角相等的条件,使AD=BE.你所添加的条件是________.
16.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是________.
三.解答题(共7题,共66分)
17(本题6分).尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置点P,到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).
18(本题8分).如图,AD是△ABC的高线,AE是角平分线,若∠BAC︰∠B︰∠C=6︰3︰1,求∠DAE的度数.
19(本题8分)如图所示,在△ABC中,∠C=90°,D是AB边上的一点,DE⊥AB于点D,交AC于点M,且ED=AC,过点E作EF∥BC分别交AB,AC于点F,N.
(1)试说明:△ABC≌△EFD.(2)若∠A=25°,求∠EMN的度数.
20(本题10分)如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG;
(2)求出∠FHG的度数.
21(本题19分)已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,
(1)求证:△ABC≌△EDF;(2)当∠CHD=120°,猜想△HDB的形状,并说明理由.
22(本题12分).如图,在中,如果BD,CE分别是,的平分线且他们相交于点P,设.
(1)当时,求的度数.
(2)求的度数,(用含n的代数式表示).
(3)当时,求证:.
23.(本题12分)如图,在⊿ABC中,∠B=∠C
,已知AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
参考答案
一、选择题
1-5D
BAD
B
6-10ACACD
二.填空题
11:如果a,b互为相反数,那么a+b=0.
12:32
13:52.
14:75°.
15:
∠A=∠B或∠ADC=∠BEC或CE=CD.
16:
4.
三.解答题
17.解析:(1)①分别以A、D为圆心,以大于AD为半径画圆,两圆相交于E、F两点;
②连接EF,则EF即为线段AD的垂直平分线.
(
2
)①以B为圆心,以大于任意长为半径画圆,分别交AB、BC为G、H;
②分别以G、H为圆心,以大于GH为半径画圆,两圆相交于点I,连接BI,则BI即为∠ABC的平分线.③BI与EF相交于点P,则点P即为所求点.
18.解析:∵∠C=180°×=18°,
∴∠B=3×18°=54°,∠BAC=6×18°=108°.
∵AD是高线,
∴∠ADB=90°,
∴∠BAD=180°-90°-54°=36°.
∵AE是角平分线,
∴∠BAE=∠BAC=×108°=54°,
∴∠DAE=∠BAE-∠DAE=54°-36°=18°.
19.解析:(1)∵DE⊥AB于点D,∴∠EDF=90°.
∵∠C=90°,∴∠C=∠EDF.
∵EF∥BC,∴∠B=∠EFD.
在△ABC和△EFD中,
∵
∴△ABC≌△EFD(AAS).
(2)∵∠EDF=90°,∴∠ADM=180°-∠EDF=90°.
在△ADM中,∠A+∠AMD+∠ADM=180°,且∠A=25°,
∴∠AMD=180°-∠A-∠ADM=65°.
∴∠EMN=∠AMD=65°.
20.解析:(1)∵在△CBF和△DBG中,
,
∴△CBF≌△DBG(SAS),∴CF=DG;
(2)∵△CBF≌△DBG,∴∠BCF=∠BDG,
又∵∠CFB=∠DFH,又∵△BCF中,
∠CBF=180°-∠BCF-∠CFB,△DHF中,
∠DHF=180°-∠BDG-∠DFH,
∴∠DHF=∠CBF=60°,
∴∠FHG=180°-∠DHF=180°-60°=120°.
21解析:(1)∵AD=BE,
∴AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SAS);
(2)∵△ABC≌△EDF,
∴∠HDB=∠HBD,
∵∠CHD=∠HDB+∠HBD=120°,
∴∠HBD=∠HDB=60°,
∴△DHB是等边三角形.
22.解析:(1)∵是的平分线
∴
同理
∴
∴
当时,
即
(2)∵,
∴
∴
(3)在线段上截取,使得
当时,
在与中
∴(SAS)
∴
又∵
∴
在与中
∴(ASA)
∴
∴,即
23.解析:(1)①t=1,BP=CQ=3,
∵AB=10,∴BD=5,∴PC=BD,
又AB=AC,∠B=∠C,∴△BPD≌△CQP(SAS)
②因两速度不等,∴,又因两三角形全等,即,
即当P运动到BC的中点时,,∴运动时间为,
∴,∴
∴当运动时间为时,时,两三角形全等;
(3)设运动时间为,∴,解得:
∴P运动距离为
∴经过的时间,在AB边上相遇,此时点P共运动了80cm.
第一章:三角形的初步知识单元测试
(时间:100分钟 满分:120分)
一.选择题(每小题3分,共30分)
1.已知AB=1.5,AC=4.5,若BC的长为整数,则BC的长为()
A.3
B.6
C.3或6
D.3或4或5或6
2.一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是()
A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形
3.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为()
A.80°
B.90°
C.100°
D.102°
,第4题图) ,第5题图) ,第6题图)
4.如图,△ABC的平分线AD与中线BE交于点O,有下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线,下列说法正确的是(
)
A.①②都正确B.①不正确,②正确
C.①②都不正确D.①正确,②不正确
5.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为(
)
A.20°
B.30°
C.35°
D.40°
6.要测量河两岸的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,使A,C,E在同一条直线上(如图),可以证明△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长.在这里判定△ABC≌△EDC的条件是(
)
A.ASA
B.SAS
C.SSS
D.以上答案均不正确
7.如图,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中能使△ABC≌△DEF的条件共有()
A.1组B.2组C.3组D.4组
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是()
A.3
B.4
C.6
D.5
,第7题图) ,第8题图) ,第9题图) ,第10题图)
9.如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是()
A.24°
B.30°
C.32°
D.36°[]
10.两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB.小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD.其中正确的结论有()
A.0个B.1个C.2个D.3个
二、填空题(每小题4分,共24分)
11.命题“如果a+b=0,那么a,b互为相反数”的逆命题为________.
12.等腰三角形的两边长分别为6cm,13cm,其周长为________cm.
13.如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=________度.
14.将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为________.
15.如图,AC=BC,请你添加一对边或一对角相等的条件,使AD=BE.你所添加的条件是________.
16.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是________.
三.解答题(共7题,共66分)
17(本题6分).尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置点P,到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).
18(本题8分).如图,AD是△ABC的高线,AE是角平分线,若∠BAC︰∠B︰∠C=6︰3︰1,求∠DAE的度数.
19(本题8分)如图所示,在△ABC中,∠C=90°,D是AB边上的一点,DE⊥AB于点D,交AC于点M,且ED=AC,过点E作EF∥BC分别交AB,AC于点F,N.
(1)试说明:△ABC≌△EFD.(2)若∠A=25°,求∠EMN的度数.
20(本题10分)如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG;
(2)求出∠FHG的度数.
21(本题19分)已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,
(1)求证:△ABC≌△EDF;(2)当∠CHD=120°,猜想△HDB的形状,并说明理由.
22(本题12分).如图,在中,如果BD,CE分别是,的平分线且他们相交于点P,设.
(1)当时,求的度数.
(2)求的度数,(用含n的代数式表示).
(3)当时,求证:.
23.(本题12分)如图,在⊿ABC中,∠B=∠C
,已知AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
参考答案
一、选择题
1-5D
BAD
B
6-10ACACD
二.填空题
11:如果a,b互为相反数,那么a+b=0.
12:32
13:52.
14:75°.
15:
∠A=∠B或∠ADC=∠BEC或CE=CD.
16:
4.
三.解答题
17.解析:(1)①分别以A、D为圆心,以大于AD为半径画圆,两圆相交于E、F两点;
②连接EF,则EF即为线段AD的垂直平分线.
(
2
)①以B为圆心,以大于任意长为半径画圆,分别交AB、BC为G、H;
②分别以G、H为圆心,以大于GH为半径画圆,两圆相交于点I,连接BI,则BI即为∠ABC的平分线.③BI与EF相交于点P,则点P即为所求点.
18.解析:∵∠C=180°×=18°,
∴∠B=3×18°=54°,∠BAC=6×18°=108°.
∵AD是高线,
∴∠ADB=90°,
∴∠BAD=180°-90°-54°=36°.
∵AE是角平分线,
∴∠BAE=∠BAC=×108°=54°,
∴∠DAE=∠BAE-∠DAE=54°-36°=18°.
19.解析:(1)∵DE⊥AB于点D,∴∠EDF=90°.
∵∠C=90°,∴∠C=∠EDF.
∵EF∥BC,∴∠B=∠EFD.
在△ABC和△EFD中,
∵
∴△ABC≌△EFD(AAS).
(2)∵∠EDF=90°,∴∠ADM=180°-∠EDF=90°.
在△ADM中,∠A+∠AMD+∠ADM=180°,且∠A=25°,
∴∠AMD=180°-∠A-∠ADM=65°.
∴∠EMN=∠AMD=65°.
20.解析:(1)∵在△CBF和△DBG中,
,
∴△CBF≌△DBG(SAS),∴CF=DG;
(2)∵△CBF≌△DBG,∴∠BCF=∠BDG,
又∵∠CFB=∠DFH,又∵△BCF中,
∠CBF=180°-∠BCF-∠CFB,△DHF中,
∠DHF=180°-∠BDG-∠DFH,
∴∠DHF=∠CBF=60°,
∴∠FHG=180°-∠DHF=180°-60°=120°.
21解析:(1)∵AD=BE,
∴AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SAS);
(2)∵△ABC≌△EDF,
∴∠HDB=∠HBD,
∵∠CHD=∠HDB+∠HBD=120°,
∴∠HBD=∠HDB=60°,
∴△DHB是等边三角形.
22.解析:(1)∵是的平分线
∴
同理
∴
∴
当时,
即
(2)∵,
∴
∴
(3)在线段上截取,使得
当时,
在与中
∴(SAS)
∴
又∵
∴
在与中
∴(ASA)
∴
∴,即
23.解析:(1)①t=1,BP=CQ=3,
∵AB=10,∴BD=5,∴PC=BD,
又AB=AC,∠B=∠C,∴△BPD≌△CQP(SAS)
②因两速度不等,∴,又因两三角形全等,即,
即当P运动到BC的中点时,,∴运动时间为,
∴,∴
∴当运动时间为时,时,两三角形全等;
(3)设运动时间为,∴,解得:
∴P运动距离为
∴经过的时间,在AB边上相遇,此时点P共运动了80cm.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
