2021-2022学年浙教新版八年级上册数学《第4章 图形与坐标》单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年浙教新版八年级上册数学《第4章 图形与坐标》单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-29 23:29:12 | ||
图片预览




文档简介
2021-2022学年浙教新版八年级上册数学《第4章
图形与坐标》单元测试卷
一.选择题
1.点P(﹣3,5)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.如图中的一张脸,小明说:“如果我用(0,2)表示左眼,用(2,2)表示右眼”,那么嘴的位置可以表示成( )
A.(0,1)
B.(2,1)
C.(1,0)
D.(1,﹣1)
3.在平面直角坐标系中,点P(5,﹣1)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.点P(3,﹣4)在平面直角坐标系中所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.一个长方形在平面直角坐标系中,三个顶点的坐标分别是(﹣1,﹣1)、(﹣1,2)、(3,﹣1),则第四个顶点的坐标是( )
A.(2,2)
B.(3,3)
C.(3,2)
D.(2,3)
6.已知点A(0,﹣6),点B(0,3),则A,B两点间的距离是( )
A.﹣9
B.9
C.﹣3
D.3
7.如果点P(﹣m,3)与点P1(﹣5,n)关于y轴对称,则m,n的值分别为( )
A.m=﹣5,n=3
B.m=5,n=3
C.m=﹣5,n=﹣3
D.m=﹣3,n=5
8.课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(1,1)表示,小军的位置用(3,2)表示,那么小刚的位置可以表示成( )
A.(5,4)
B.(4,5)
C.(3,4)
D.(4,3)
9.下列说法正确的是( )
A.若ab=0,则点P(a,b)表示原点
B.点(1,﹣a2)一定在第四象限
C.已知点A(1,﹣3)与点B(1,3),则直线AB平行y轴
D.已知点A(1,﹣3),AB∥y轴,且AB=4,则B点的坐标为(1,1)
10.如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)…根据这个规律,第2021个点的坐标为( )
A.(45,9)
B.(45,4)
C.(45,21)
D.(45,0)
二.填空题
11.如图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(﹣2,﹣1),白棋③的坐标是(﹣1,﹣3),则黑棋②的坐标是
.
12.已知点P(﹣3,2),则点P到x轴的距离为
,到y轴的距离为
.
13.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为
.
14.点A(1﹣a,5)和点B(3,b)关于y轴对称,则a+b=
.
15.在平面直角坐标系中,若点P(x﹣2,x)在第二象限,则x的取值范围为
.
16.如图,平面直角坐标系中O是原点,等边△OAB的顶点A的坐标是(2,0),动点P从点O出发,以每秒1个单位长度的速度,沿O→A→B→O→A…的路线作循环运动,则第2021秒时,点P的坐标是
.
17.若教室中的5排3列记为(5,3),则3排5列记为
.
18.在平面直角坐标系中,点P(2,﹣3)在第
象限.
19.已知直线AB∥x轴,A点的坐标为(2,1),并且线段AB=2,则点B的坐标为
.
20.平面直角坐标系中,点A(0,﹣1)与点B(3,3)之间的距离是
.
三.解答题
21.已知点P(8﹣2m,m﹣1).
(1)若点P在x轴上,求m的值.
(2)若点P到两坐标轴的距离相等,求P点的坐标.
22.如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系:
(2)B同学家的坐标是
;
(3)在你所建立的直角坐标系中,如果C同学家的坐标为(﹣150,100),请你在图中描出表示C同学家的点.
23.如图,是某校的平面示意图,已知图书馆、行政楼的坐标分别为(﹣3,2),(2,3).完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他地点的坐标;
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置.
24.在平面直角坐标系中,一只蜗牛从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示:
(1)填写下列各点的坐标:A5(
,
),A9(
,
),A13(
,
);
(2)写出点A4n+1的坐标(n是正整数);
(3)指出蜗牛从点A2020到点A2021的移动方向.
25.已知:点P(2m+4,m﹣1).试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过A(2,﹣3)点,且与x轴平行的直线上.
26.在平面直角坐标系中,点A(1,2a+3)在第一象限.
(1)若点A到x轴的距离与到y轴的距离相等,求a的值;
(2)若点A到x轴的距离小于到y轴的距离,求a的取值范围.
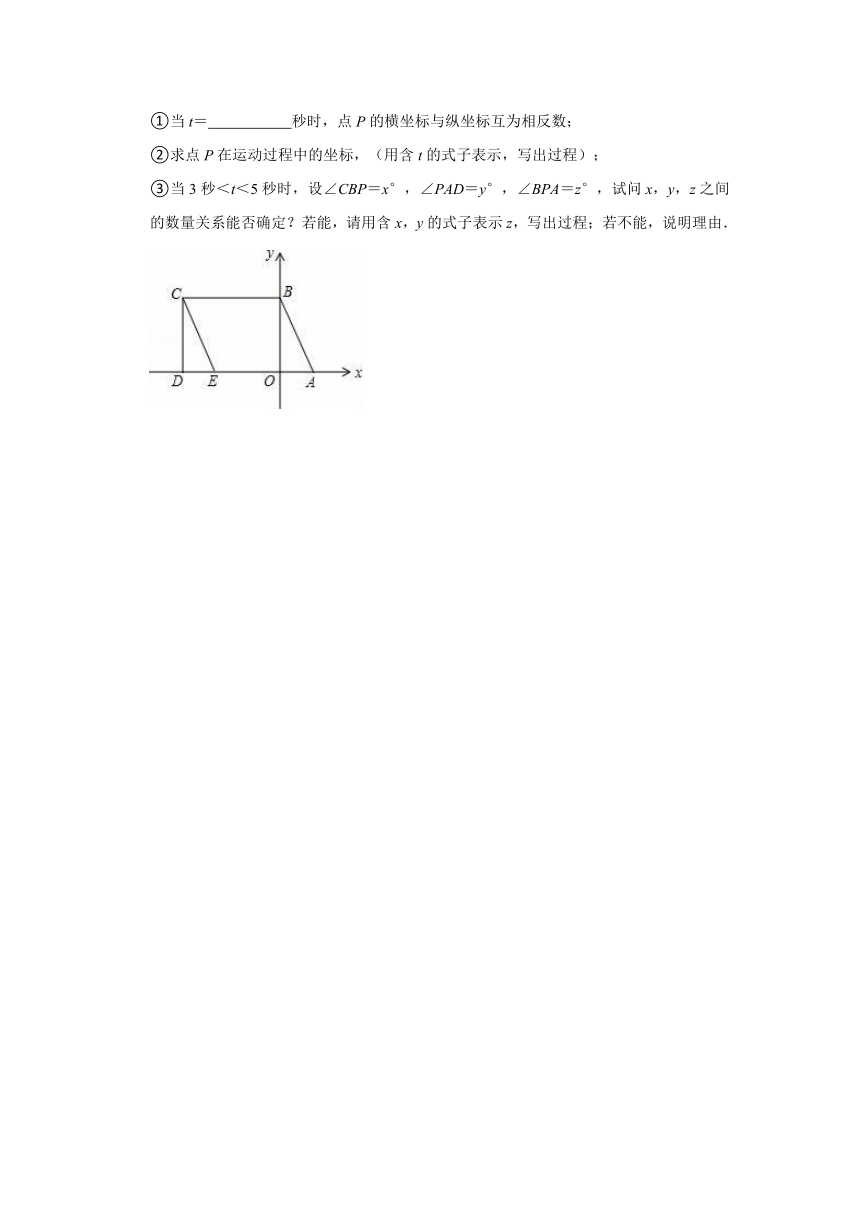
27.如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标
;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t=
秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.
参考答案与试题解析
一.选择题
1.解:点P(﹣3,5)所在的象限是第二象限.
故选:B.
2.解:如图,
嘴的位置可以表示成(1,0).
故选:C.
3.解:∵点P的横坐标是正数,纵坐标是负数,
∴点P(5,﹣1)在第四象限,
故选:D.
4.解:∵3>0,﹣4<0,
∴点P(3,﹣4)所在的象限是第四象限.
故选:D.
5.解:过(﹣1,2)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(3,2),即为第四个顶点坐标.
故选:C.
6.解:∵A(0,﹣6),点B(0,3),
∴A,B两点间的距离=3﹣(﹣6)=9.
故选:B.
7.解:点P和点P1关于y轴对称,
根据题意,有n=3,﹣m=5;
即m=﹣5,n=3;
故选:A.
8.解:根据小华的位置用(1,1)表示,小军的位置用(3,2)表示,
那么小刚的位置可以用坐标表示成(5,4).
故选:A.
9.解:A、若ab=0,则点P(a,b)表示在坐标轴上,故此选项错误;
B、点(1,﹣a2)一定在第四象限或x轴上,故此选项错误;
C、已知点A(1,﹣3)与点B(1,3),则直线AB平行y轴,正确;
D、已知点A(1,﹣3),AB∥y轴,且AB=4,则B点的坐标为(1,1)或(1,﹣7),故此选项错误.
故选:C.
10.解:观察图形可知,到每一个横坐标结束,经过整数点的个数等于最后横坐标的平方,
横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,
横坐标为偶数时以横坐标为1,纵坐标以横坐标减1结束,
∴横坐标以n结束的有n2个点,
第2025个点是(45,0),
∴2021个点的坐标是(45,4);
故选:B.
二.填空题
11.解:由用(﹣2,﹣1)表示白棋①的位置,用(﹣1,﹣3)表示白棋③的位置知,y轴为从左向数的第四条竖直直线,且向上为正方向,x轴是从下往上数第五条水平直线,这两条直线交点为坐标原点.那么黑棋②的位置为(1,﹣2).
故答案为:(1,﹣2).
12.解:∵点P的坐标为(﹣3,2),
∴点P到x轴的距离为|2|=2,到y轴的距离为|﹣3|=3.故填:2、3.
13.解:已知AB∥x轴,点B的纵坐标与点A的纵坐标相同,都是2;
在直线AB上,过点A向左5单位得(﹣2,2),过点A向右5单位得(8,2).
∴满足条件的点有两个:(﹣2,2),(8,2).故答案填:(﹣2,2)或(8,2).
14.解:∵点A(1﹣a,5)与B(3,b)关于y轴对称
∴a=4,b=5
∴a+b=4+5=9.
15.解:因为点P(x﹣2,x)在第二象限,所以,解得0<x<2.
16.解:由题意得,第1秒结束时P点的坐标为P1(1,0);
第2秒结束时P点的坐标为P2(2,0);
第3秒结束时P点的坐标为P3(2﹣1×cos60°,1×sin60°),即P3(,);
第4秒结束时P点的坐标为P4(1,2×sin60°),即P4(1,);
第5秒结束时P点的坐标为P5(,);
第6秒结束时P点的坐标为P6(0,0);
第7秒结束时P点的坐标为P7(1,0),与P1相同;
……
由上可知,P点的坐标按每6秒进行循环,
∵2021÷6=336……5,
∴第2021秒结束后,点P的坐标与P5相同为(,),
故答案为:(,).
17.解:∵5排3列记为(5,3),
∴3排5列记为(3,5).
故答案为:(3,5).
18.解:点P(2,﹣3)在第四象限.
故答案为:四.
19.解:∵AB∥x轴,点A坐标为(2,1),
∴A,B的纵坐标相等为1,
设点B的横坐标为x,则有AB=|x﹣2|=2,
解得:x=4或0,
∴点B的坐标为(4,1)或(0,1).
故答案为:(4,1)或(0,1).
20.解:AB==5.
故答案为5.
三.解答题
21.解:(1)∵点P(8﹣2m,m﹣1)在x轴上,
∴m﹣1=0,
解得:m=1;
(2)∵点P到两坐标轴的距离相等,
∴|8﹣2m|=|m﹣1|,
∴8﹣2m=m﹣1或8﹣2m=1﹣m,
解得:m=3或m=7,
∴P(2,2)或(﹣6,6).
22.解:(1)如图,
(2)B同学家的坐标是(200,150);
(3)如图.
故答案为(200,150).
23.解:(1)如图所示:
(2)根据坐标系得出:
校门口(0,0),实验楼(﹣4,0),综合楼(﹣5,﹣3),信息楼(1,﹣2);
(3)如图所示:.
24.解:(1)根据点的坐标变化可知:
各点的坐标为:A5(2,1),A9(4,1),A13(6,1);
故答案为:2,1,4,1,6,1;
(2)根据(1)发现:
点A4n+1的坐标(n为正整数)为(2n,1);
(3)因为每四个点一个循环,
所以2021÷4=505…1.
所以蜗牛从点A2020到点A2021的移动方向是向上.
25.解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3);
(2)令m﹣1=0,解得m=1,所以P点的坐标为(6,0);
(3)令m﹣1=(2m+4)+3,解得m=﹣8,所以P点的坐标为(﹣12,﹣9);
(4)令m﹣1=﹣3,解得m=﹣2.所以P点的坐标为(0,﹣3).
26.解:(1)∵点A到x轴的距离与到y轴的距离相等,
∴2a+3=1,
解得a=﹣1;
(2)∵点A到x轴的距离小于到y轴的距离,点A在第一象限,
∴2a+3<1且2a+3>0,
解得a<﹣1且a>﹣,
∴﹣<a<﹣1.
27.解:(1)根据题意,可得
三角形OAB沿x轴负方向平移3个单位得到三角形DEC,
∵点A的坐标是(1,0),
∴点E的坐标是(﹣2,0);
故答案为:(﹣2,0);
(2)①∵点C的坐标为(﹣3,2)
∴BC=3,CD=2,
∵点P的横坐标与纵坐标互为相反数;
∴点P在线段BC上,
∴PB=CD,
即t=2;
∴当t=2秒时,点P的横坐标与纵坐标互为相反数;
故答案为:2;
②当点P在线段BC上时,点P的坐标(﹣t,2),
当点P在线段CD上时,点P的坐标(﹣3,5﹣t);
③能确定,
如图,过P作PF∥BC交AB于F,
则PF∥AD,
∴∠1=∠CBP=x°,∠2=∠DAP=y°,
∴∠BPA=∠1+∠2=x°+y°=z°,
∴z=x+y.
图形与坐标》单元测试卷
一.选择题
1.点P(﹣3,5)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.如图中的一张脸,小明说:“如果我用(0,2)表示左眼,用(2,2)表示右眼”,那么嘴的位置可以表示成( )
A.(0,1)
B.(2,1)
C.(1,0)
D.(1,﹣1)
3.在平面直角坐标系中,点P(5,﹣1)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.点P(3,﹣4)在平面直角坐标系中所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.一个长方形在平面直角坐标系中,三个顶点的坐标分别是(﹣1,﹣1)、(﹣1,2)、(3,﹣1),则第四个顶点的坐标是( )
A.(2,2)
B.(3,3)
C.(3,2)
D.(2,3)
6.已知点A(0,﹣6),点B(0,3),则A,B两点间的距离是( )
A.﹣9
B.9
C.﹣3
D.3
7.如果点P(﹣m,3)与点P1(﹣5,n)关于y轴对称,则m,n的值分别为( )
A.m=﹣5,n=3
B.m=5,n=3
C.m=﹣5,n=﹣3
D.m=﹣3,n=5
8.课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(1,1)表示,小军的位置用(3,2)表示,那么小刚的位置可以表示成( )
A.(5,4)
B.(4,5)
C.(3,4)
D.(4,3)
9.下列说法正确的是( )
A.若ab=0,则点P(a,b)表示原点
B.点(1,﹣a2)一定在第四象限
C.已知点A(1,﹣3)与点B(1,3),则直线AB平行y轴
D.已知点A(1,﹣3),AB∥y轴,且AB=4,则B点的坐标为(1,1)
10.如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)…根据这个规律,第2021个点的坐标为( )
A.(45,9)
B.(45,4)
C.(45,21)
D.(45,0)
二.填空题
11.如图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(﹣2,﹣1),白棋③的坐标是(﹣1,﹣3),则黑棋②的坐标是
.
12.已知点P(﹣3,2),则点P到x轴的距离为
,到y轴的距离为
.
13.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为
.
14.点A(1﹣a,5)和点B(3,b)关于y轴对称,则a+b=
.
15.在平面直角坐标系中,若点P(x﹣2,x)在第二象限,则x的取值范围为
.
16.如图,平面直角坐标系中O是原点,等边△OAB的顶点A的坐标是(2,0),动点P从点O出发,以每秒1个单位长度的速度,沿O→A→B→O→A…的路线作循环运动,则第2021秒时,点P的坐标是
.
17.若教室中的5排3列记为(5,3),则3排5列记为
.
18.在平面直角坐标系中,点P(2,﹣3)在第
象限.
19.已知直线AB∥x轴,A点的坐标为(2,1),并且线段AB=2,则点B的坐标为
.
20.平面直角坐标系中,点A(0,﹣1)与点B(3,3)之间的距离是
.
三.解答题
21.已知点P(8﹣2m,m﹣1).
(1)若点P在x轴上,求m的值.
(2)若点P到两坐标轴的距离相等,求P点的坐标.
22.如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
(1)以学校为坐标原点,向东为x轴正方向,向北为y轴正方向,在图中建立平面直角坐标系:
(2)B同学家的坐标是
;
(3)在你所建立的直角坐标系中,如果C同学家的坐标为(﹣150,100),请你在图中描出表示C同学家的点.
23.如图,是某校的平面示意图,已知图书馆、行政楼的坐标分别为(﹣3,2),(2,3).完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他地点的坐标;
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置.
24.在平面直角坐标系中,一只蜗牛从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示:
(1)填写下列各点的坐标:A5(
,
),A9(
,
),A13(
,
);
(2)写出点A4n+1的坐标(n是正整数);
(3)指出蜗牛从点A2020到点A2021的移动方向.
25.已知:点P(2m+4,m﹣1).试分别根据下列条件,求出P点的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大3;
(4)点P在过A(2,﹣3)点,且与x轴平行的直线上.
26.在平面直角坐标系中,点A(1,2a+3)在第一象限.
(1)若点A到x轴的距离与到y轴的距离相等,求a的值;
(2)若点A到x轴的距离小于到y轴的距离,求a的取值范围.
27.如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标
;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t=
秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.
参考答案与试题解析
一.选择题
1.解:点P(﹣3,5)所在的象限是第二象限.
故选:B.
2.解:如图,
嘴的位置可以表示成(1,0).
故选:C.
3.解:∵点P的横坐标是正数,纵坐标是负数,
∴点P(5,﹣1)在第四象限,
故选:D.
4.解:∵3>0,﹣4<0,
∴点P(3,﹣4)所在的象限是第四象限.
故选:D.
5.解:过(﹣1,2)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(3,2),即为第四个顶点坐标.
故选:C.
6.解:∵A(0,﹣6),点B(0,3),
∴A,B两点间的距离=3﹣(﹣6)=9.
故选:B.
7.解:点P和点P1关于y轴对称,
根据题意,有n=3,﹣m=5;
即m=﹣5,n=3;
故选:A.
8.解:根据小华的位置用(1,1)表示,小军的位置用(3,2)表示,
那么小刚的位置可以用坐标表示成(5,4).
故选:A.
9.解:A、若ab=0,则点P(a,b)表示在坐标轴上,故此选项错误;
B、点(1,﹣a2)一定在第四象限或x轴上,故此选项错误;
C、已知点A(1,﹣3)与点B(1,3),则直线AB平行y轴,正确;
D、已知点A(1,﹣3),AB∥y轴,且AB=4,则B点的坐标为(1,1)或(1,﹣7),故此选项错误.
故选:C.
10.解:观察图形可知,到每一个横坐标结束,经过整数点的个数等于最后横坐标的平方,
横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,
横坐标为偶数时以横坐标为1,纵坐标以横坐标减1结束,
∴横坐标以n结束的有n2个点,
第2025个点是(45,0),
∴2021个点的坐标是(45,4);
故选:B.
二.填空题
11.解:由用(﹣2,﹣1)表示白棋①的位置,用(﹣1,﹣3)表示白棋③的位置知,y轴为从左向数的第四条竖直直线,且向上为正方向,x轴是从下往上数第五条水平直线,这两条直线交点为坐标原点.那么黑棋②的位置为(1,﹣2).
故答案为:(1,﹣2).
12.解:∵点P的坐标为(﹣3,2),
∴点P到x轴的距离为|2|=2,到y轴的距离为|﹣3|=3.故填:2、3.
13.解:已知AB∥x轴,点B的纵坐标与点A的纵坐标相同,都是2;
在直线AB上,过点A向左5单位得(﹣2,2),过点A向右5单位得(8,2).
∴满足条件的点有两个:(﹣2,2),(8,2).故答案填:(﹣2,2)或(8,2).
14.解:∵点A(1﹣a,5)与B(3,b)关于y轴对称
∴a=4,b=5
∴a+b=4+5=9.
15.解:因为点P(x﹣2,x)在第二象限,所以,解得0<x<2.
16.解:由题意得,第1秒结束时P点的坐标为P1(1,0);
第2秒结束时P点的坐标为P2(2,0);
第3秒结束时P点的坐标为P3(2﹣1×cos60°,1×sin60°),即P3(,);
第4秒结束时P点的坐标为P4(1,2×sin60°),即P4(1,);
第5秒结束时P点的坐标为P5(,);
第6秒结束时P点的坐标为P6(0,0);
第7秒结束时P点的坐标为P7(1,0),与P1相同;
……
由上可知,P点的坐标按每6秒进行循环,
∵2021÷6=336……5,
∴第2021秒结束后,点P的坐标与P5相同为(,),
故答案为:(,).
17.解:∵5排3列记为(5,3),
∴3排5列记为(3,5).
故答案为:(3,5).
18.解:点P(2,﹣3)在第四象限.
故答案为:四.
19.解:∵AB∥x轴,点A坐标为(2,1),
∴A,B的纵坐标相等为1,
设点B的横坐标为x,则有AB=|x﹣2|=2,
解得:x=4或0,
∴点B的坐标为(4,1)或(0,1).
故答案为:(4,1)或(0,1).
20.解:AB==5.
故答案为5.
三.解答题
21.解:(1)∵点P(8﹣2m,m﹣1)在x轴上,
∴m﹣1=0,
解得:m=1;
(2)∵点P到两坐标轴的距离相等,
∴|8﹣2m|=|m﹣1|,
∴8﹣2m=m﹣1或8﹣2m=1﹣m,
解得:m=3或m=7,
∴P(2,2)或(﹣6,6).
22.解:(1)如图,
(2)B同学家的坐标是(200,150);
(3)如图.
故答案为(200,150).
23.解:(1)如图所示:
(2)根据坐标系得出:
校门口(0,0),实验楼(﹣4,0),综合楼(﹣5,﹣3),信息楼(1,﹣2);
(3)如图所示:.
24.解:(1)根据点的坐标变化可知:
各点的坐标为:A5(2,1),A9(4,1),A13(6,1);
故答案为:2,1,4,1,6,1;
(2)根据(1)发现:
点A4n+1的坐标(n为正整数)为(2n,1);
(3)因为每四个点一个循环,
所以2021÷4=505…1.
所以蜗牛从点A2020到点A2021的移动方向是向上.
25.解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3);
(2)令m﹣1=0,解得m=1,所以P点的坐标为(6,0);
(3)令m﹣1=(2m+4)+3,解得m=﹣8,所以P点的坐标为(﹣12,﹣9);
(4)令m﹣1=﹣3,解得m=﹣2.所以P点的坐标为(0,﹣3).
26.解:(1)∵点A到x轴的距离与到y轴的距离相等,
∴2a+3=1,
解得a=﹣1;
(2)∵点A到x轴的距离小于到y轴的距离,点A在第一象限,
∴2a+3<1且2a+3>0,
解得a<﹣1且a>﹣,
∴﹣<a<﹣1.
27.解:(1)根据题意,可得
三角形OAB沿x轴负方向平移3个单位得到三角形DEC,
∵点A的坐标是(1,0),
∴点E的坐标是(﹣2,0);
故答案为:(﹣2,0);
(2)①∵点C的坐标为(﹣3,2)
∴BC=3,CD=2,
∵点P的横坐标与纵坐标互为相反数;
∴点P在线段BC上,
∴PB=CD,
即t=2;
∴当t=2秒时,点P的横坐标与纵坐标互为相反数;
故答案为:2;
②当点P在线段BC上时,点P的坐标(﹣t,2),
当点P在线段CD上时,点P的坐标(﹣3,5﹣t);
③能确定,
如图,过P作PF∥BC交AB于F,
则PF∥AD,
∴∠1=∠CBP=x°,∠2=∠DAP=y°,
∴∠BPA=∠1+∠2=x°+y°=z°,
∴z=x+y.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
