2.6 直角三角形 课时练习 2021—2022学年浙教版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 2.6 直角三角形 课时练习 2021—2022学年浙教版数学八年级上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 77.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 18:10:49 | ||
图片预览


文档简介
浙教版数学八年级上册2.6
《直角三角形》课时练习
一、选择题
1.使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
2.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A=2∠B=2∠C
C.∠A∶∠B∶∠C=1∶2∶3
D.∠A=∠B=3∠C
3.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中直角三角形有( )
A.0个 B.1个 C.2个 D.3个
4.直角三角形两个锐角平分线相交所成的钝角的度数为( )
A.120° B.135° C.150° D.120°或135°
5.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km C.0.9 km D.1.2 km
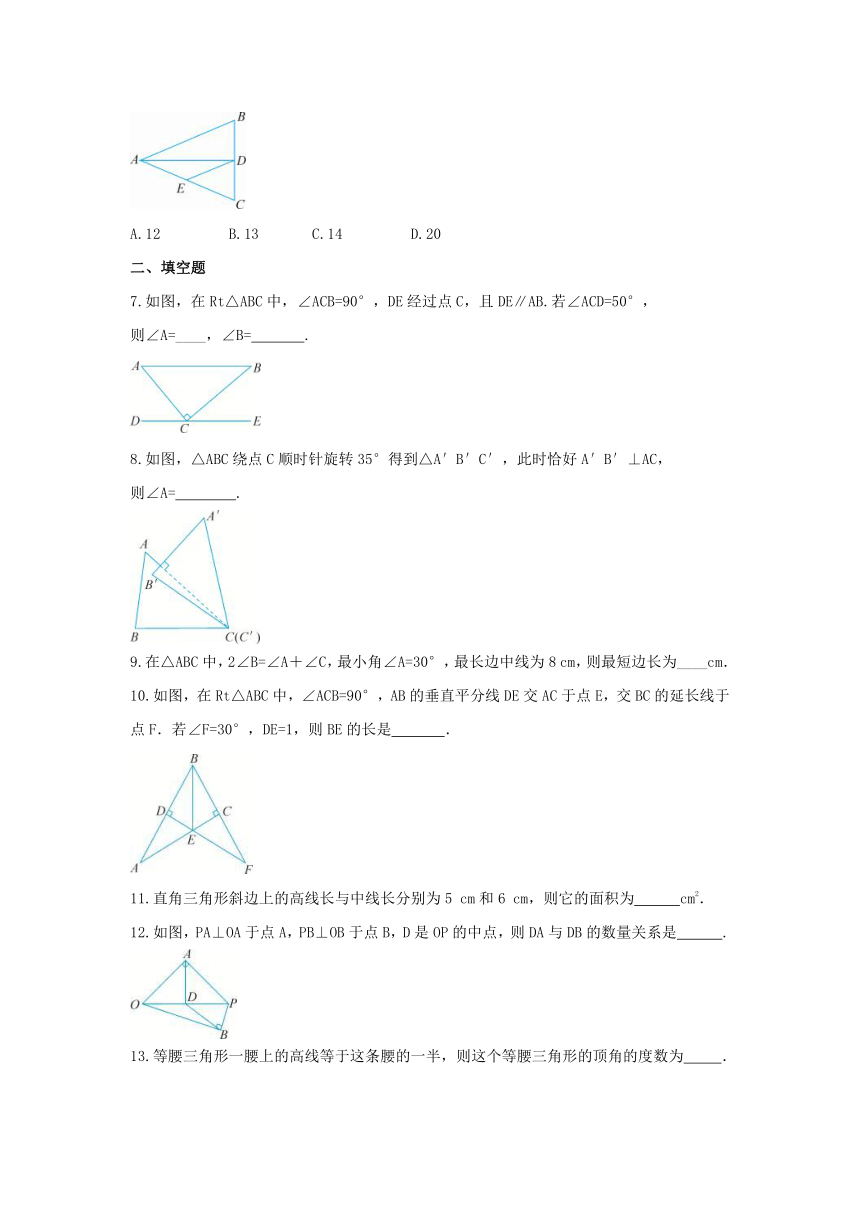
6.如图,在△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,E为AC的中点,连结DE,则△CDE的周长为( )
A.12 B.13 C.14 D.20
二、填空题
7.如图,在Rt△ABC中,∠ACB=90°,DE经过点C,且DE∥AB.若∠ACD=50°,
则∠A=____,∠B= .
8.如图,△ABC绕点C顺时针旋转35°得到△A′B′C′,此时恰好A′B′⊥AC,
则∠A= .
9.在△ABC中,2∠B=∠A+∠C,最小角∠A=30°,最长边中线为8 cm,则最短边长为____cm.
10.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于点E,交BC的延长线于点F.若∠F=30°,DE=1,则BE的长是 .
11.直角三角形斜边上的高线长与中线长分别为5 cm和6 cm,则它的面积为 cm2.
12.如图,PA⊥OA于点A,PB⊥OB于点B,D是OP的中点,则DA与DB的数量关系是 .
13.等腰三角形一腰上的高线等于这条腰的一半,则这个等腰三角形的顶角的度数为 .
14.如图,在等边三角形ABC中,D,E分别为AB,BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则= .
三、解答题
15.如图,CE⊥AD,垂足为E,∠A=∠C.求证:△ABD是直角三角形.
16.如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.求证:△PEF是直角三角形.
17.如图,在Rt△ABC中,∠C=90°,AB的中垂线DE交BC于点D,垂足为E,
且∠CAD∶∠CAB=1∶3,求∠B的度数.
18.如图,在△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F,连结DF.求证:AB垂直平分DF.
参考答案
1.答案为:D
2.答案为:D.
3.答案为:D.
4.答案为:B.
5.答案为:D.
6.答案为:C.
7.答案为:50°,40°;
8.答案为:55°.
9.答案为:8.
10.答案为:2.
11.答案为:30.
12.答案为:DA=DB.
13.答案为:30°或150°.
14.答案为:.
15.证明:∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°.
又∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.
16.证明:∵AB∥CD,
∴∠BEF+∠DFE=180°.
∵∠BEF的平分线与∠DFE的平分线相交于点P,
∴∠PEF=∠BEF,∠PFE=∠DFE,
∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°.
∴△PEF是直角三角形.
17.解:设∠CAD=x°,
则∠CAB=3x°,∠BAD=2x°.
∵DE是AB的中垂线,
∴DA=DB,
∴∠B=∠BAD=2x°.
∵∠C=90°,
∴∠CAB+∠B=90°,
即3x+2x=90,
解得x=18,
∴∠B=2×18°=36°.
18.证明:∵∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°,∠CAD+∠CDE=90°.
∵CE⊥AD,
∴∠CED=90°.
∴∠CDE+∠DCE=90°.
∴∠CAD=∠DCE,即∠CAD=∠BCF.
∵BF∥AC,
∴∠CBF+∠ACB=180°,
∴∠CBF=180°-∠ACB=90°.
∴∠CBF=∠ACD.
在△ACD和△CBF中,
∵
∴△ACD≌△CBF(ASA).
∴CD=BF.
∵D为BC的中点,
∴CD=BD,
∴BD=BF.
∵BF∥AC,
∴∠ABF=∠CAB=∠DBA=45°.
∴AB垂直平分DF.
《直角三角形》课时练习
一、选择题
1.使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
2.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C
B.∠A=2∠B=2∠C
C.∠A∶∠B∶∠C=1∶2∶3
D.∠A=∠B=3∠C
3.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中直角三角形有( )
A.0个 B.1个 C.2个 D.3个
4.直角三角形两个锐角平分线相交所成的钝角的度数为( )
A.120° B.135° C.150° D.120°或135°
5.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得AM的长为1.2 km,则M,C两点间的距离为( )
A.0.5 km B.0.6 km C.0.9 km D.1.2 km
6.如图,在△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,E为AC的中点,连结DE,则△CDE的周长为( )
A.12 B.13 C.14 D.20
二、填空题
7.如图,在Rt△ABC中,∠ACB=90°,DE经过点C,且DE∥AB.若∠ACD=50°,
则∠A=____,∠B= .
8.如图,△ABC绕点C顺时针旋转35°得到△A′B′C′,此时恰好A′B′⊥AC,
则∠A= .
9.在△ABC中,2∠B=∠A+∠C,最小角∠A=30°,最长边中线为8 cm,则最短边长为____cm.
10.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于点E,交BC的延长线于点F.若∠F=30°,DE=1,则BE的长是 .
11.直角三角形斜边上的高线长与中线长分别为5 cm和6 cm,则它的面积为 cm2.
12.如图,PA⊥OA于点A,PB⊥OB于点B,D是OP的中点,则DA与DB的数量关系是 .
13.等腰三角形一腰上的高线等于这条腰的一半,则这个等腰三角形的顶角的度数为 .
14.如图,在等边三角形ABC中,D,E分别为AB,BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则= .
三、解答题
15.如图,CE⊥AD,垂足为E,∠A=∠C.求证:△ABD是直角三角形.
16.如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.求证:△PEF是直角三角形.
17.如图,在Rt△ABC中,∠C=90°,AB的中垂线DE交BC于点D,垂足为E,
且∠CAD∶∠CAB=1∶3,求∠B的度数.
18.如图,在△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F,连结DF.求证:AB垂直平分DF.
参考答案
1.答案为:D
2.答案为:D.
3.答案为:D.
4.答案为:B.
5.答案为:D.
6.答案为:C.
7.答案为:50°,40°;
8.答案为:55°.
9.答案为:8.
10.答案为:2.
11.答案为:30.
12.答案为:DA=DB.
13.答案为:30°或150°.
14.答案为:.
15.证明:∵CE⊥AD,
∴∠CED=90°,
∴∠C+∠D=90°.
又∵∠A=∠C,
∴∠A+∠D=90°,
∴△ABD是直角三角形.
16.证明:∵AB∥CD,
∴∠BEF+∠DFE=180°.
∵∠BEF的平分线与∠DFE的平分线相交于点P,
∴∠PEF=∠BEF,∠PFE=∠DFE,
∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°.
∴△PEF是直角三角形.
17.解:设∠CAD=x°,
则∠CAB=3x°,∠BAD=2x°.
∵DE是AB的中垂线,
∴DA=DB,
∴∠B=∠BAD=2x°.
∵∠C=90°,
∴∠CAB+∠B=90°,
即3x+2x=90,
解得x=18,
∴∠B=2×18°=36°.
18.证明:∵∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°,∠CAD+∠CDE=90°.
∵CE⊥AD,
∴∠CED=90°.
∴∠CDE+∠DCE=90°.
∴∠CAD=∠DCE,即∠CAD=∠BCF.
∵BF∥AC,
∴∠CBF+∠ACB=180°,
∴∠CBF=180°-∠ACB=90°.
∴∠CBF=∠ACD.
在△ACD和△CBF中,
∵
∴△ACD≌△CBF(ASA).
∴CD=BF.
∵D为BC的中点,
∴CD=BD,
∴BD=BF.
∵BF∥AC,
∴∠ABF=∠CAB=∠DBA=45°.
∴AB垂直平分DF.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
