1.4全等三角形

(共33张PPT)
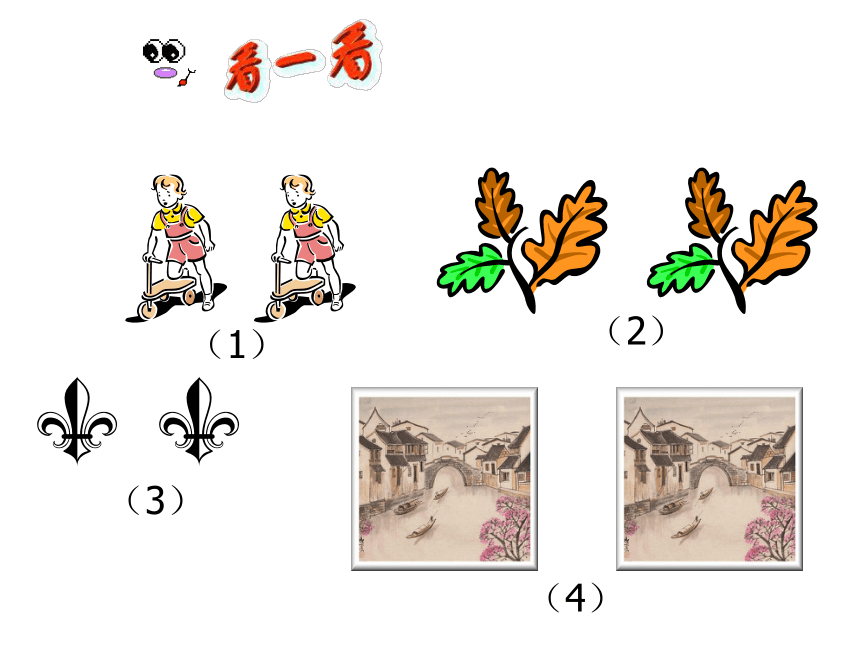
仔细观察下列各组图形，你发现了什么？
每组图形的形状和大小完全相同。
（1）
（2）
（3）
（4）
两个能够重合的图形叫做全等图形.
全等图形的形状和大小完全相同.
形状相同,但大小不同,
因此它们不是全等图形.
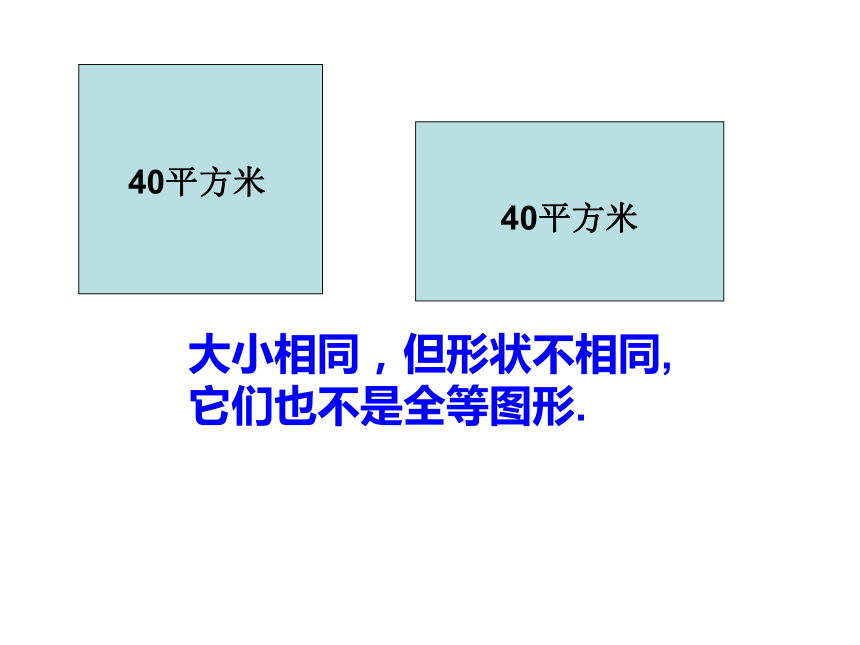
大小相同，但形状不相同,它们也不是全等图形.
40平方米
40平方米
大小相同，形状也相同,它们是全等图形.
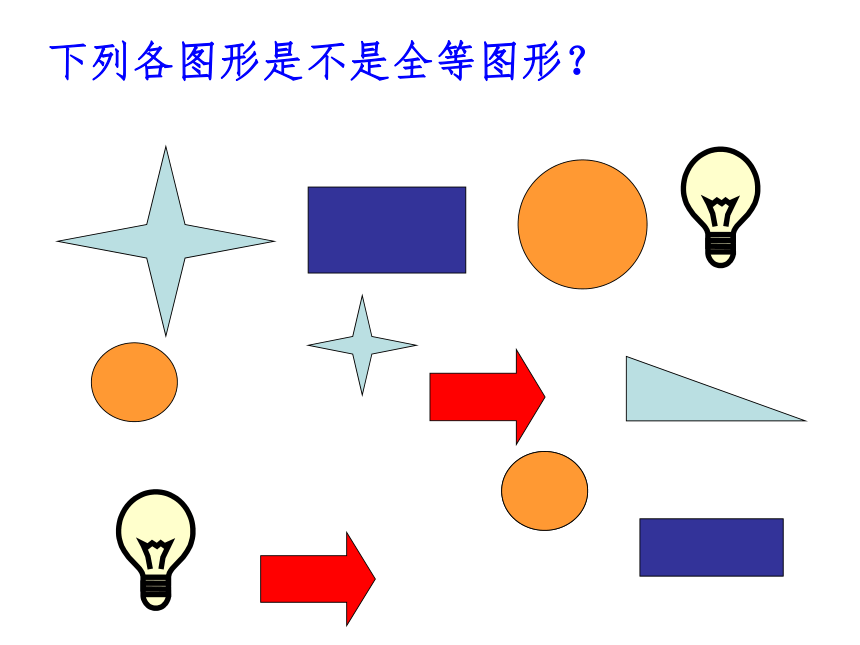
下列各图形是不是全等图形？
F
E
D
C
B
A
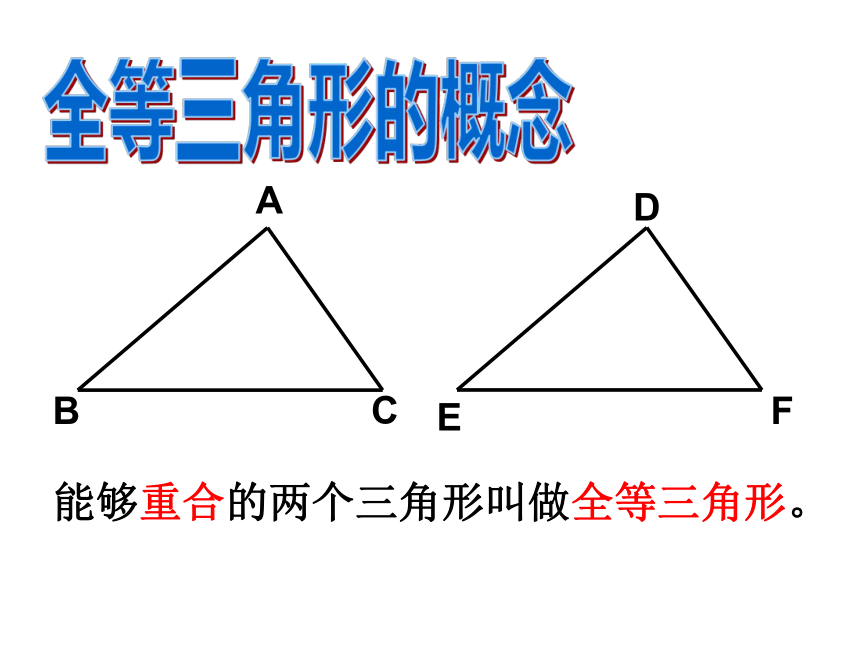
能够重合的两个三角形叫做全等三角形。
它们会全等吗？
小试身手
下列说法是否正确,并简要说明理由:
(1) 边长相等的正方形都是全等图形.
(2) 同一面中华人民共和国国旗上,4个小五角星都是全等图形.
(3) 面积相等的两个三角形是全等三角形.
(4) 两个全等三角形的面积相等
对
对
错
对
A
B
C
D
E
F
如果△ ABC 与△DEF会互相重合，顶点A与顶点(　)重合，顶点B与顶点(　)重合，顶点C与顶点(　）重合。
AB边与(　　）边重合， BC边与(　　）边重合，AC边与（　　）边重合。
∠ A与(　　）重合，∠B与(　　)重合，∠C与 (　　）重合。
D
E
F
DE
EF
DF
∠D
∠E
∠F
两个全等三角形重合时,互相重合的顶点叫对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。
“全等”用符号“≌ ”表示
记两个全等三角形时，通常把表示对应顶点的字母写在对应的位置上。
比如△ABC≌△DFE
A
B
C
D
E
F
△ABC≌△DEF
试一试,摆一摆
用符号来表示两个全等三角形：
C
A
B
D
O
O
A
C
D
B
△AOC
≌
△DOB
△AOC
≌
△BOD
1、若△AOC≌△BOD，对应
边是___________________，对应角是________________；
A
B
O
C
D
2、若△ABD≌△ACD，对应边是_________________________，对应角是_________________；
A
B
C
D
3、若△ABC≌△CDA,对应
边是________________，对应角是_______________；
A
B
C
D
AC与BD,AO与BO,CO与DO
∠A与∠B, ∠ C与∠ D, ∠ AOC与∠ BOD
AB与AC,BD与CD,AD与AD
∠BAD 与∠CAD, ∠B与 ∠C, ∠ADB与∠ADC
AB与CD,BC与DA,AC与CA
1
2
3
4
∠1与 ∠2, ∠3 与∠4, ∠ B与 ∠ D
　　两个全等三角形的位置变化了，对应边、对应角的大小有变化吗？由此你能得到什么结论？
全等三角形的对应边相等，对应角相等。
∵△ABC≌ △DFE
∴ AB= , =FE, AC=
（　　　　　　　　　　　）
∠ A= ∠ D, ∠ B= ∠ ,
∠ = ∠ E
（ ）
全等三角形的性质
全等三角形的对应边相等
全等三角形的对应角相等
DF
BC
DE
F
C
例 如图, AD平分∠BAC，AB=AC，△ABD与△ACD全等吗？BD与CD相等吗？∠B与∠C呢？请说明理由。
A
B
C
D
解: ∵AD平分∠BAC
∴ ∠1= ∠2,
∵ AB=AC
∴点C与点B重合,
又∵ 点A与点A重合，点D与点D重合
∴ △ABD ≌ △ACD
∴BD=CD 　　　　　　　　
1
2
判断两个三角形全等；可利用全等三角形的概念。
∴△ABD与△ACD重合
（全等三角形的意义）
（全等三角形的对应边相等）
∴∠B=∠C
（全等三角形的对应角相等）
因此将图形沿AD对折时,射线AC与射线AB重合.
如图，在△ABC中，AD⊥BC于点D，BD=CD,则∠B= ∠C,请完成说理过程：
解：∵ AD⊥BC（已知），
A
B
C
D
∵BD=CD( )
∴点B与点＿＿＿重合
∴△ABD与△ACD＿＿＿＿
∠ADC
重合
已知
C
重合
≌
全等三角形的对应角相等
又∵点A与点＿重合，点＿与点＿重合。
∴∠ADB=＿＿＿＿=Rt ∠(垂线的意义）
当把图形沿AD对折时，射线DB与DC____
∴ △ABD____△ACD（全等三角形的意义），
∴ ∠B=∠C（　　　　　　　　　　　）
A
D
D
一、选择题
△ABC≌ △BAD，A和B、C和D是对应点，如果
AB=5cm，BD=4cm，AD=6cm，那么BC的长是
（　）
（A）6cm （B）5cm （C）4cm （ D）无法确定
A
在上题中， ∠CAB的对应角是（　　　）
　(A)∠DAB　 (B) ∠ DBA
　(C) ∠ DBC (D) ∠ CAD
A
O
C
D
B
B
二、如图，△ABC≌△AEC， ∠B=30°,∠ ACB=85°,求出△AEC各内角的度数.
B
A
C
E
右图是一个等边三角形，你能把它分成两个全等的三角形吗？你能把它分成三个、四个全等的三角形吗？
通过自己的努力，这节课你获得了哪些知识？你还存在哪些疑惑？请说一说。
　愿同学们：每天学到一点新知识，每天拥有一份好心情！