3.8《弧长及扇形的面积》课时练习2021-2022学年浙教版数学九年级上册(Word版含答案)
文档属性
| 名称 | 3.8《弧长及扇形的面积》课时练习2021-2022学年浙教版数学九年级上册(Word版含答案) | 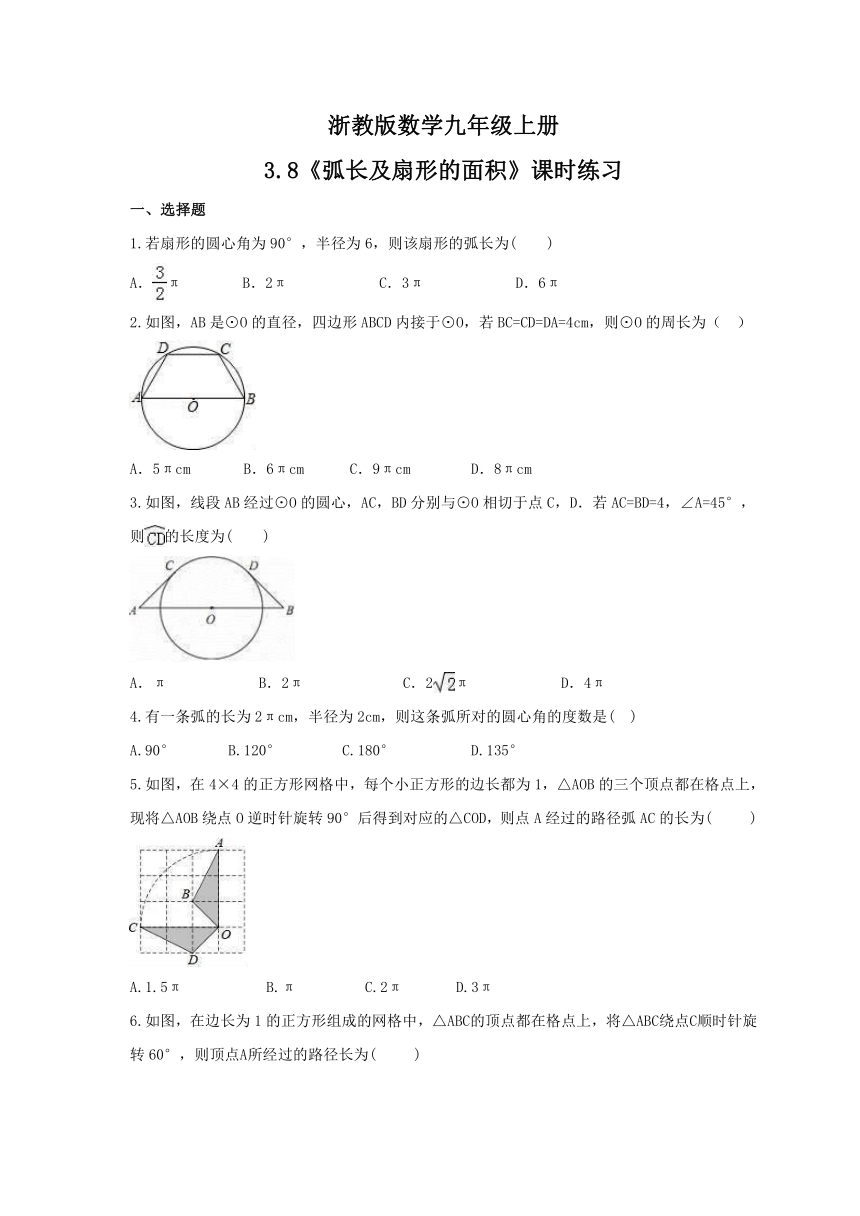 | |
| 格式 | zip | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-31 17:34:24 | ||
图片预览



文档简介
浙教版数学九年级上册
3.8《弧长及扇形的面积》课时练习
一、选择题
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π??
?
B.2π??
???
C.3π??
??
D.6π
2.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为(
)
A.5πcm
B.6πcm
C.9πcm
D.8πcm
3.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π???
??
B.2π????
?
C.2π???
??
D.4π
4.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是(
)
A.90°
B.120°
C.180°
D.135°
5.如图,在4×4的正方形网格中,每个小正方形的边长都为1,△AOB的三个顶点都在格点上,现将△AOB绕点O逆时针旋转90°后得到对应的△COD,则点A经过的路径弧AC的长为(
)
A.1.5π?????
B.π????
C.2π???
D.3π
6.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为(
)
A.10π
B.
C.π
D.π
7.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是(
)
A.甲先到B点
B.乙先到B点
C.甲、乙同时到B
D.无法确定
8.如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为(
)
A.3
B.6
C.3π
D.6π
二、填空题
9.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为
.
10.扇形的圆心角为120°,弧长为6πcm,那么这个扇形的面积为
cm2.
11.已知扇形的半径为6cm,圆心角的度数为120°,则此扇形的弧长为
cm.
12.如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=4cm.则图中阴影部分面积为 ??
.(结果保留π)
13.挂钟分针的长10cm,经过45分钟,它的针尖转过的弧长是
cm.
14.如图,在△ABC中,AB=6,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是 .
三、解答题
15.如图,AB是⊙O的直径,点C是圆上一点,连接CA、CB,过点O作弦BC的垂线,交于点D,连接AD.
(1)求证:∠CAD=∠BAD;
(2)若⊙O的半径为1,∠B=50°,求的长.
16.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求弧AC的长.
17.如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).
18.如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).
参考答案
1.答案为:C.
2.答案为:D
3.答案为:B.
4.答案为:C;
5.答案为:A
6.答案为:C;
7.答案为:C
8.答案为:A
9.答案为:3π.
10.答案为:6π×9÷2=27πcm2.
11.答案为:4π.
12.答案为:πcm2.
13.答案为:15π.
14.答案是:6π.
15.(1)证明:∵点O是圆心,OD⊥BC,
∴,
∴∠CAD=∠BAD;
(2)连接CO,
∵∠B=50°,
∴∠AOC=100°,
∴的长为:L=.
16.解:(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∵OC∥BD,
∴∠AEO=∠ADB=90°,
即OC⊥AD,
∴AE=ED.
(2)∵OC⊥AD,
∴=,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴==2π.
17.(1)证明:连接OD,如图所示.
∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.
∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∴∠CFD=∠ODF=90°,∴DF⊥AC.
(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.
∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,
∴的长===π.
18.(1)证明:连接OD,如图所示.
∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.
∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∴∠CFD=∠ODF=90°,∴DF⊥AC.
(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.
∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,∴的长===π.
3.8《弧长及扇形的面积》课时练习
一、选择题
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π??
?
B.2π??
???
C.3π??
??
D.6π
2.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为(
)
A.5πcm
B.6πcm
C.9πcm
D.8πcm
3.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π???
??
B.2π????
?
C.2π???
??
D.4π
4.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是(
)
A.90°
B.120°
C.180°
D.135°
5.如图,在4×4的正方形网格中,每个小正方形的边长都为1,△AOB的三个顶点都在格点上,现将△AOB绕点O逆时针旋转90°后得到对应的△COD,则点A经过的路径弧AC的长为(
)
A.1.5π?????
B.π????
C.2π???
D.3π
6.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为(
)
A.10π
B.
C.π
D.π
7.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是(
)
A.甲先到B点
B.乙先到B点
C.甲、乙同时到B
D.无法确定
8.如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为(
)
A.3
B.6
C.3π
D.6π
二、填空题
9.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为
.
10.扇形的圆心角为120°,弧长为6πcm,那么这个扇形的面积为
cm2.
11.已知扇形的半径为6cm,圆心角的度数为120°,则此扇形的弧长为
cm.
12.如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=4cm.则图中阴影部分面积为 ??
.(结果保留π)
13.挂钟分针的长10cm,经过45分钟,它的针尖转过的弧长是
cm.
14.如图,在△ABC中,AB=6,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是 .
三、解答题
15.如图,AB是⊙O的直径,点C是圆上一点,连接CA、CB,过点O作弦BC的垂线,交于点D,连接AD.
(1)求证:∠CAD=∠BAD;
(2)若⊙O的半径为1,∠B=50°,求的长.
16.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求弧AC的长.
17.如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).
18.如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).
参考答案
1.答案为:C.
2.答案为:D
3.答案为:B.
4.答案为:C;
5.答案为:A
6.答案为:C;
7.答案为:C
8.答案为:A
9.答案为:3π.
10.答案为:6π×9÷2=27πcm2.
11.答案为:4π.
12.答案为:πcm2.
13.答案为:15π.
14.答案是:6π.
15.(1)证明:∵点O是圆心,OD⊥BC,
∴,
∴∠CAD=∠BAD;
(2)连接CO,
∵∠B=50°,
∴∠AOC=100°,
∴的长为:L=.
16.解:(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°.
∵OC∥BD,
∴∠AEO=∠ADB=90°,
即OC⊥AD,
∴AE=ED.
(2)∵OC⊥AD,
∴=,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴==2π.
17.(1)证明:连接OD,如图所示.
∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.
∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∴∠CFD=∠ODF=90°,∴DF⊥AC.
(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.
∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,
∴的长===π.
18.(1)证明:连接OD,如图所示.
∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.
∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∴∠CFD=∠ODF=90°,∴DF⊥AC.
(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.
∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,∴的长===π.
同课章节目录
