2021-2022学年浙教版九年级数学上册1.2 二次函数的图象同步检测(word版附答案)
文档属性
| 名称 | 2021-2022学年浙教版九年级数学上册1.2 二次函数的图象同步检测(word版附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 995.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-02 18:45:33 | ||
图片预览

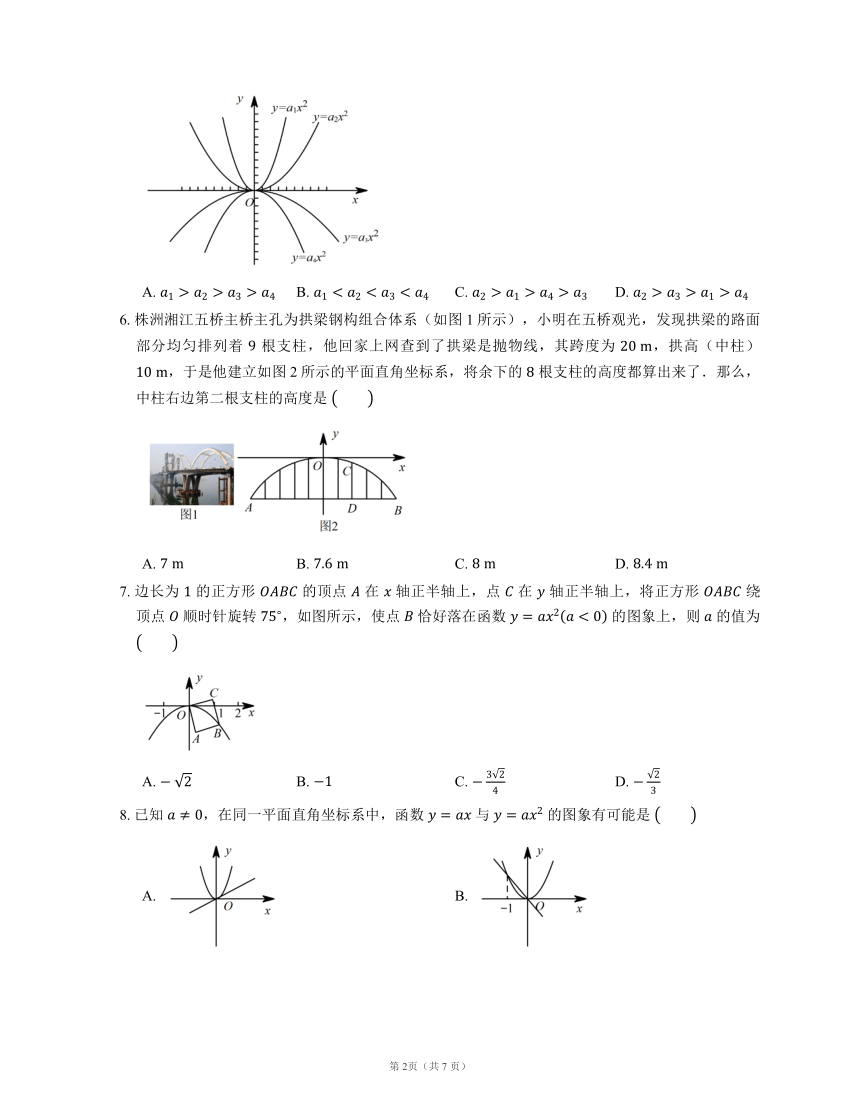
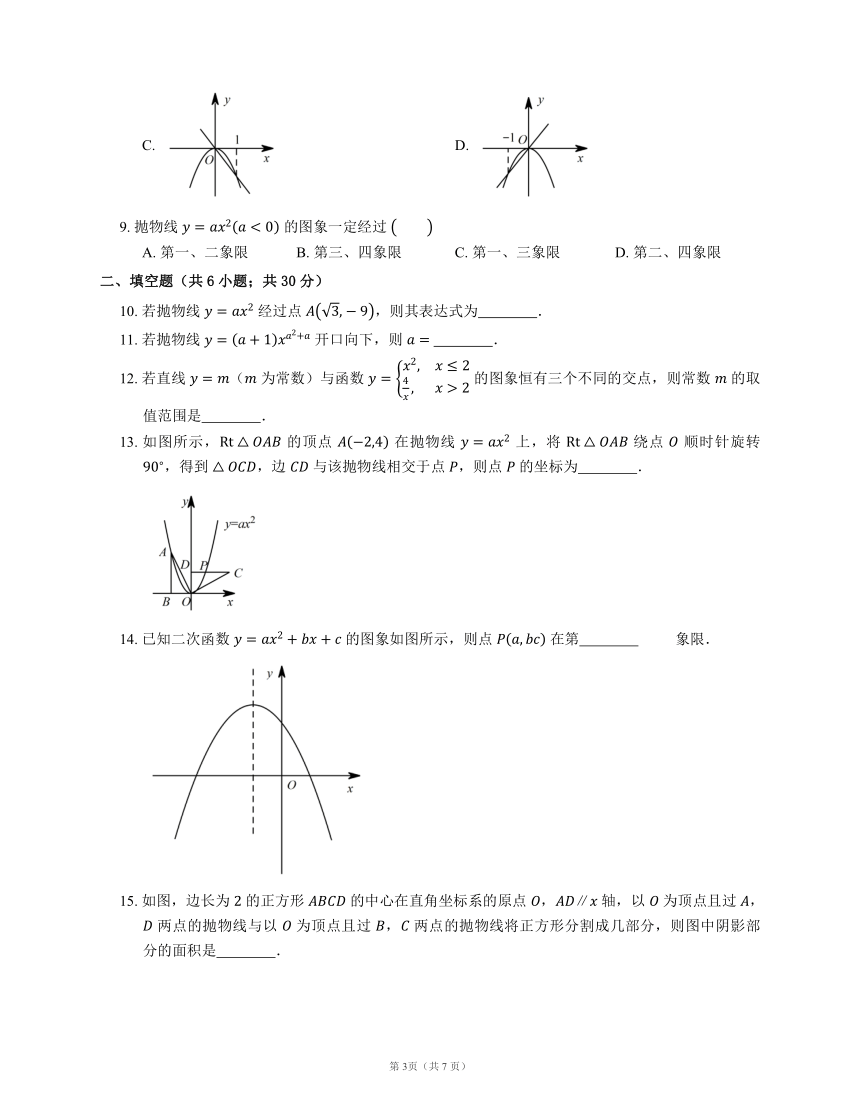
文档简介
1.2
二次函数的图象
一、选择题(共9小题;共45分)
1.
已知抛物线
经过点
,那么
的值是
A.
B.
C.
D.
2.
函数
与
在同一平面直角坐标系中的图象可能是
A.
B.
C.
D.
3.
在同一平面直角坐标系中作函数
,,
的图象,这些图象的共同特点是
A.
都是关于
轴对称,抛物线开口向上
B.
都是关于
轴对称,抛物线的顶点都是原点
C.
都是关于原点对称,抛物线的顶点都是原点
D.
都是关于
轴对称,抛物线开口向下
4.
某车的刹车距离
与开始刹车时的速度
之间满足二次函数
,若该车某次的刹车距离为
,则刹车前的速度为
A.
B.
C.
D.
5.
已知四个二次函数的图象如图所示,那么
,,,
的大小关系是
A.
B.
C.
D.
6.
株洲湘江五桥主桥主孔为拱梁钢构组合体系(如图1所示),小明在五桥观光,发现拱梁的路面部分均匀排列着
根支柱,他回家上网查到了拱梁是抛物线,其跨度为
,拱高(中柱),于是他建立如图2所示的平面直角坐标系,将余下的
根支柱的高度都算出来了.那么,中柱右边第二根支柱的高度是
A.
B.
C.
D.
7.
边长为
的正方形
的顶点
在
轴正半轴上,点
在
轴正半轴上,将正方形
绕顶点
顺时针旋转
,如图所示,使点
恰好落在函数
的图象上,则
的值为
A.
B.
C.
D.
8.
已知
,在同一平面直角坐标系中,函数
与
的图象有可能是
A.
B.
C.
D.
9.
抛物线
的图象一定经过
A.
第一、二象限
B.
第三、四象限
C.
第一、三象限
D.
第二、四象限
二、填空题(共6小题;共30分)
10.
若抛物线
经过点
,则其表达式为
?.
11.
若抛物线
开口向下,则
?.
12.
若直线
(
为常数)与函数
的图象恒有三个不同的交点,则常数
的取值范围是
?.
13.
如图所示,
的顶点
在抛物线
上,将
绕点
顺时针旋转
,得到
,边
与该抛物线相交于点
,则点
的坐标为
?.
14.
已知二次函数
的图象如图所示,则点
在第
?
象限.
15.
如图,边长为
的正方形
的中心在直角坐标系的原点
,
轴,以
为顶点且过
,
两点的抛物线与以
为顶点且过
,
两点的抛物线将正方形分割成几部分,则图中阴影部分的面积是
?.
三、解答题(共5小题;共75分)
16.
根据下列条件,求
的值或取值范围:
(1)函数
,当
时,
随
增大而减小;当
时,
随
增大而增大.
(2)函数
有最大值.
(3)抛物线
与抛物线
的形状相同.
(4)函数
的图象是开口向上的抛物线.
17.
已知二次函数
的图象经过点
.
(1)求这个二次函数的表达式并画出其图象.
(2)请写出这个二次函数的顶点坐标及对称轴.
18.
已知函数
与直线
交于点
.
(1)求
和
的值;
(2)当
取何值时,二次函数
中的
随
的增大而增大?
(3)求抛物线
与直线
的另一个交点
的坐标.
19.
有一座横断面为抛物线形状的拱桥,其水面宽
为
,拱顶
离水面
的距离
为
,货船在水面以上部分的横断面是矩形
,建立如图所示的平面直角坐标系.
(1)求此抛物线的二次函数表达式.
(2)如果限定矩形的长
为
,那么矩形的高
不能超过多少米,才能使船通过拱桥?
(3)若设
,请将矩形
的面积
用含
的代数式表示,并指出
的取值范围.
20.
如图所示,在平面直角坐标系中,
为坐标原点,直线
交
轴于点
,在抛物线
上是否存在一点
,使
的面积等于
?若存在,求出点
的坐标;若不存在,说明理由.
答案
1.
B
2.
D
【解析】
时,
的函数图象位于第一、三象限,
的函数图象位于第一、二象限且经过原点,
时,
的函数图象位于第二、四象限,
的函数图象位于第三、四象限且经过原点,纵观各选项,只有
D
选项图形符合.
3.
B
4.
C
5.
A
6.
D
7.
D
8.
C
9.
B
10.
11.
12.
13.
14.
三
15.
16.
(1)
.
??????(2)
.
??????(3)
.
??????(4)
.
17.
(1)
将点
代入
,得
,
则函数表达式为
.
如图所示:
??????(2)
顶点坐标为
,对称轴为直线
.
18.
(1)
,.
??????(2)
因为
,
所以二次函数
为
,它的图象开口向下,对称轴为
轴,
所以当
时,
随
的增大而增大.
??????(3)
解方程组
得
所以抛物线
与直线
的另一个交点
的坐标是
.
19.
(1)
.
??????(2)
,
点
的横坐标为
,
则点
的纵坐标为
.
点
的坐标为
.
要使货船能通过拱桥,则货船高度不能超过
.
??????(3)
,
点
坐标为
.
.
20.
假设存在一点
,使
,
,
即
,解得
,
把
代入
,解得
,
点
的坐标为:
或
.
第1页(共7
页)
二次函数的图象
一、选择题(共9小题;共45分)
1.
已知抛物线
经过点
,那么
的值是
A.
B.
C.
D.
2.
函数
与
在同一平面直角坐标系中的图象可能是
A.
B.
C.
D.
3.
在同一平面直角坐标系中作函数
,,
的图象,这些图象的共同特点是
A.
都是关于
轴对称,抛物线开口向上
B.
都是关于
轴对称,抛物线的顶点都是原点
C.
都是关于原点对称,抛物线的顶点都是原点
D.
都是关于
轴对称,抛物线开口向下
4.
某车的刹车距离
与开始刹车时的速度
之间满足二次函数
,若该车某次的刹车距离为
,则刹车前的速度为
A.
B.
C.
D.
5.
已知四个二次函数的图象如图所示,那么
,,,
的大小关系是
A.
B.
C.
D.
6.
株洲湘江五桥主桥主孔为拱梁钢构组合体系(如图1所示),小明在五桥观光,发现拱梁的路面部分均匀排列着
根支柱,他回家上网查到了拱梁是抛物线,其跨度为
,拱高(中柱),于是他建立如图2所示的平面直角坐标系,将余下的
根支柱的高度都算出来了.那么,中柱右边第二根支柱的高度是
A.
B.
C.
D.
7.
边长为
的正方形
的顶点
在
轴正半轴上,点
在
轴正半轴上,将正方形
绕顶点
顺时针旋转
,如图所示,使点
恰好落在函数
的图象上,则
的值为
A.
B.
C.
D.
8.
已知
,在同一平面直角坐标系中,函数
与
的图象有可能是
A.
B.
C.
D.
9.
抛物线
的图象一定经过
A.
第一、二象限
B.
第三、四象限
C.
第一、三象限
D.
第二、四象限
二、填空题(共6小题;共30分)
10.
若抛物线
经过点
,则其表达式为
?.
11.
若抛物线
开口向下,则
?.
12.
若直线
(
为常数)与函数
的图象恒有三个不同的交点,则常数
的取值范围是
?.
13.
如图所示,
的顶点
在抛物线
上,将
绕点
顺时针旋转
,得到
,边
与该抛物线相交于点
,则点
的坐标为
?.
14.
已知二次函数
的图象如图所示,则点
在第
?
象限.
15.
如图,边长为
的正方形
的中心在直角坐标系的原点
,
轴,以
为顶点且过
,
两点的抛物线与以
为顶点且过
,
两点的抛物线将正方形分割成几部分,则图中阴影部分的面积是
?.
三、解答题(共5小题;共75分)
16.
根据下列条件,求
的值或取值范围:
(1)函数
,当
时,
随
增大而减小;当
时,
随
增大而增大.
(2)函数
有最大值.
(3)抛物线
与抛物线
的形状相同.
(4)函数
的图象是开口向上的抛物线.
17.
已知二次函数
的图象经过点
.
(1)求这个二次函数的表达式并画出其图象.
(2)请写出这个二次函数的顶点坐标及对称轴.
18.
已知函数
与直线
交于点
.
(1)求
和
的值;
(2)当
取何值时,二次函数
中的
随
的增大而增大?
(3)求抛物线
与直线
的另一个交点
的坐标.
19.
有一座横断面为抛物线形状的拱桥,其水面宽
为
,拱顶
离水面
的距离
为
,货船在水面以上部分的横断面是矩形
,建立如图所示的平面直角坐标系.
(1)求此抛物线的二次函数表达式.
(2)如果限定矩形的长
为
,那么矩形的高
不能超过多少米,才能使船通过拱桥?
(3)若设
,请将矩形
的面积
用含
的代数式表示,并指出
的取值范围.
20.
如图所示,在平面直角坐标系中,
为坐标原点,直线
交
轴于点
,在抛物线
上是否存在一点
,使
的面积等于
?若存在,求出点
的坐标;若不存在,说明理由.
答案
1.
B
2.
D
【解析】
时,
的函数图象位于第一、三象限,
的函数图象位于第一、二象限且经过原点,
时,
的函数图象位于第二、四象限,
的函数图象位于第三、四象限且经过原点,纵观各选项,只有
D
选项图形符合.
3.
B
4.
C
5.
A
6.
D
7.
D
8.
C
9.
B
10.
11.
12.
13.
14.
三
15.
16.
(1)
.
??????(2)
.
??????(3)
.
??????(4)
.
17.
(1)
将点
代入
,得
,
则函数表达式为
.
如图所示:
??????(2)
顶点坐标为
,对称轴为直线
.
18.
(1)
,.
??????(2)
因为
,
所以二次函数
为
,它的图象开口向下,对称轴为
轴,
所以当
时,
随
的增大而增大.
??????(3)
解方程组
得
所以抛物线
与直线
的另一个交点
的坐标是
.
19.
(1)
.
??????(2)
,
点
的横坐标为
,
则点
的纵坐标为
.
点
的坐标为
.
要使货船能通过拱桥,则货船高度不能超过
.
??????(3)
,
点
坐标为
.
.
20.
假设存在一点
,使
,
,
即
,解得
,
把
代入
,解得
,
点
的坐标为:
或
.
第1页(共7
页)
同课章节目录
